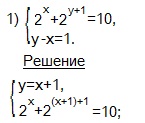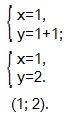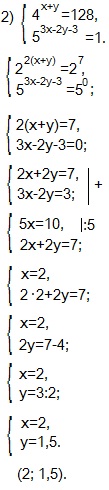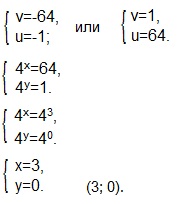Системы показательных уравнений 11 класс

Видео:Показательные уравнения. 11 класс.Скачать

11.3.6. Решение систем показательных уравнений

Что является обязательным при решении системы показательных уравнений? Конечно, преобразование данной системы в систему простейших уравнений.

Решить системы уравнений:

Выразим у через х из (2) -го уравнения системы и подставим это значение в (1) -ое уравнение системы.

Решаем (2) -ое уравнение полученной системы:

2 х +2 x +2 =10, применяем формулу: a x + y =a x ∙a y .

2 x +2 x ∙2 2 =10, вынесем общий множитель 2 х за скобки:

2 х (1+2 2 )=10 или 2 х ∙5=10, отсюда 2 х =2.

2 х =2 1 , отсюда х=1. Возвращаемся к системе уравнений.

Ответ: (1; 2).

Представляем левую и правую части (1) -го уравнения в виде степеней с основанием 2, а правую часть (2) -го уравнения как нулевую степень числа 5.

Если равны две степени с одинаковыми основаниями, то равны и показатели этих степеней — приравниваем показатели степеней с основаниями 2 и показатели степеней с основаниями 5.

Получившуюся систему линейных уравнений с двумя переменными решаем методом сложения.

Находим х=2 и это значение подставляем вместо х во второе уравнение системы.

Находим у.

Ответ: (2; 1,5).

Если в предыдущих двух примерах мы переходили к более простой системе приравнивая показатели двух степеней с одинаковыми основаниями, то в 3-ем примере эта операция невыполнима. Такие системы удобно решать вводом новых переменных. Мы введем переменные u и v, а затем выразим переменную u через v и получим уравнение относительно переменной v.

Решаем (2) -ое уравнение системы.

v 2 +63v-64=0. Подберем корни по теореме Виета, зная, что: v₁+v₂=-63; v₁∙v₂=-64.

Получаем: v₁=-64, v₂=1. Возвращаемся к системе, находим u.

Так как значения показательной функции всегда положительны, то уравнения 4 x = -1 и 4 y = -64 решений не имеют.

Представляем 64 и 1 в виде степеней с основанием 4.

Приравниваем показатели степеней и находим х и у.

Видео:11 класс, 12 урок, Показательные уравненияСкачать

Конспект урока 11 класс «Решение показательных уравнений и систем уравнений».

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Тема: «Решение показательных уравнений и систем уравнений».

Цель: 1. Систематизировать виды показательных выражений,

рассмотреть способы решений уравнений и систем уравнений.

Научить систематизировать показательные уравнения и их системы.

Развить умение применять алгоритмы решений показательных уравнений к различным видам уравнений и их систем.

Воспитывать ответственное отношение к изучаемой теме.

Организационный момент. Сообщение темы и цели урока.

Повторение и закрепление пройденного материала.

ответы на вопросы по домашнему заданию (разбор нерешённых заданий).

Устный фронтальный опрос по теме «Показательная функция».

В.1. Какая функция называется показательной?

(ответ: Функция вида у = а х , где а о, а ≠ 1, х — переменная, называется показательной функцией).

В.2. Почему основание а не должно быть равным 1 (а ≠ 1)?

(ответ: т.к при а=1 степень а х при любом значении х равнялась бы 1 и тогда она не зависела бы от х).

В.3. Почему основание а должно быть обязательно положительным (а о)? (ответ: т.к. при а о степень а х для многих значений х не была бы действительным числом. Например а = — 5, , то а х будет , что не является действительным числом).

В.4. Какое число берётся из всех значений, если х равен дроби, а х означает корень некоторой степени?

(ответ: берётся только одно арифметическое значение, т.е. неотрицательное число).

В.5. Повторить свойства:

m =

Изучение нового материала

Определение: Показательным уравнением называется уравнение котором неизвестное Х входит только в показатель степени при некоторых постоянных основаниях.

а) 2 х = ; б) х = ; в) 3 х+1 + 3 х = 108

Способы решения показательных уравнений

Способ приведения к общему основанию

1) обе части уравнения приводим к одинаковому основанию;

2) приравниваем показатели степеней левой и правой частей уравнения, в результате чего получаем уравнение, способ решения которого известен;

3) Решаем полученное уравнение;

4) с помощью проверки определяем, какие из полученных значений переменной являются корнями данного показательного уравнения.

ПРИМЕР: 27 х = ;

1. Обе части уравнения приводим к основанию 3 (3 3 ) х =3 — 4

2. Приравниваем показатели 3х = — 4

3. Решив полученное уравнение имеем Х= —

4. Проверим:

=

=

Ответ: —

Способ введения новой переменной

Делаем замену переменной, приводящую к алгебраическому уравнению;

Решаем полученное алгебраическое уравнение;

Найденные значения корней алгебраического уравнения подставив в равенство, определяющее замену;

Найдём корни полученного уравнения;

С помощью проверки определяем, какие из этих корней являются корнями данного показательного уравнения.

ПРИМЕР: 3 2х+5 = 3 х+2 + 2

3 2х * 3 5 = 3 х * 3 2 +2

(3 х ) 2 * 243 = 3 х *9+2

243у 2 – 9*у-2 = 0 решив это уравнение, имеем

у ₁ = ; у ₂ = —

не может быть 3 х 0.

берём только у = 3 х = 3 х = 3 -2 х = -2

Используется в тех случаях, когда в показательном уравнении а х = в, число В нельзя представить в виде степени числа а. Для решения уравнения на одной координатной плоскости строят графики функций у=а х и у=в. Абсциссы точек пересечения графиков указанных функций будут решениями данного показательного уравнения.

Решение системы показательных уравнений.

умножим обе части второго уравнения на 2

+ почленно сложим уравнения

5 * =

2 х =

2 х = х=2 –подставим во второе уравнение системы

;

— ;

— ;

;

Первое уравнение почленно умножим на второе

(2 * 3) х+у =

=

у = 3 – х подставим в первое уравнение:

* = 12

= 12

= 12

х = 12

( ) х =

( ) х = ( ) 2

х = 2, у = 3 – 2 = 1. Ответ: (2;1)

Решение показательных уравнений, требующие применения различных алгебраических приёмов преобразования уравнений.

— 3 * — 10 * = 4

— можно вынести за скобки

* — * * 3 – 10 * = 4

( ) = 4

* 100 = 4

= —

Сгруппируем члены уравнение, содержащие степени числа 3, в левой части, а члены, содержащие степени числа 2, — в правой.

+ = +

+ = +

* (3+1) = * (1+ )

* 9

* = * разделим обе части этого уравнения на правую часть

= 1 по свойствам степени

= 1

= 1

= 1

( = ( ) 0

х — = 0

х =

Уравнение, решаемые разложением на множители

* * = 5400

* * = * *

Разделим обе части уравнения на его правую часть, получим

= 1 по свойствам степеней

* * = 1

* * = 1

= 90 0

Уравнения, содержащие помимо показательных другие функции.

2 *

Перенесём все члены уравнения в левую часть, сгруппируем их и вынесем общие множители за скобки и имеем:

2 * = 0

(2 * + (1- ) = 0

2 * ( ) = 0

( ) * (2 ) = 0

т.к. произведение равно 0, если хотя бы один из множителей равен 0.

= 0 или 2 = 0

2

=

х = 0 х = (-1) n arcsin + π n ,

х = (-1) n π n , n € z

Есть показательные уравнения, в которых для решения приходится вводить две новые переменные.

+ ² — 2 *

( ) 2 + ( ) 2 – 2 * * = 0

= а

получаем

а 2 + b 2 – 2 а b = 0

по формуле сокращенного умножения

(а — b ) 2 = 0 следовательно а = b

т.е. =

Уравнения, решаемые с помощью их специфики.

7 х + 24 х = 25 х

Можно угадать, что корень уравнения равен 2.

х = 2, действительно 7 2 + 24 2 = 25 2

Разделим все члены уравнения на его правую часть, получим

( ) х + ( ) х = 2

Функции ( ) х и ( ) х убывающие, т.к. основания меньше 1.

Сумма этих функций является функцией убывающей. Поэтому по теореме о корне данное уравнение имеет единственное решение. у

Уравнения, решаемые графически.

3 у ₂

построим график функции у ₁ = и у ₂ = у ₁ х

Видно, что графики этих функций пересекаются 2

в единственной точке А, абсцисса х = 2 которой

является решением данного уравнения.

Закрепление новой темы. Решить в классе упр.596,598,600,602(нечетные)

Видео:ПРОСТЕЙШИЙ способ решения Показательных УравненийСкачать

Урок по алгебре «Системы показательных уравнений и неравенств»
методическая разработка по алгебре (11 класс) по теме

Разработка содержит план урока, презентацию, а также самостоятельную работу на 2 варианта.

Цель урока:

• Обобщение и систематизация способов решения показательных уравнений;
• Формирование навыков решения систем показательных уравнений;
• Отработать умения решать задачи разной степени сложности на примере задач из ЕГЭ и КДР.
• Выявление знаний и степени усвоения материала по теме.

Видео:Системы показательных уравнений и неравенств. Видеоурок 13. Алгебра 10 классСкачать

Скачать:

Видео:Системы показательных уравнений и неравенств. Практика. Видеоуроки 13. Алгебра 10 классСкачать

Предварительный просмотр:

1. 6-0,2
2. Найдите его площадь в квадратных сантиметрах

1. 2 x =8
2. 4 x-1 =1
3. 
4. 2 4-2x =64
5. Найдите ее площадь в квадратных сантиметрах.

2. Найдите его площадь в квадратных сантиметрах.

20. Найдите ее площадь в квадратных сантиметрах.

Видео:Как решать системы показательных уравнений. Урок№ 27Скачать

По теме: методические разработки, презентации и конспекты

план урока по алгебре и началам анализа. показательные уравнение и неравенства

конспект урока по теме: «Решение показательных уравнений и неравенств». алгебра 11 класс

Используется дифференцированный метод обучения.

Обобщающий урок по теме «Решение показательных уравнений и неравенств»

Разработка открытогоурока в 10 классе с целью актуализации опорных знаний при решении показательных уравнений и неравенств. При этом проверка усвоения темы идёт на обязательном уровне. Учащиеся демонс.

Урок по теме «Решение показательных уравнений и неравенств». 11 класс.

Данная разработка содержит конспект урока обобщения и систематизации знаний по теме: «Решение показательных уравнений и неравенств» для 11 класса, общеобразовательной школы , а также презен.

Решение показательных уравнений и неравенств. Урок алгебры в 11 классе.

Отработка этого материала необходима, так как ежегодно в заданиях ЕГЭ встречается эта тема.

Презентация к уроку алгебры в 10 классе на тему «Показательная функция. Решение показательных уравнений и неравенств в рамках подготовки к ЕГЭ»

Презентация на тему «Показательная функция. Решение показательных уравнений и неравенств в рамках подготовки к ЕГЭ» является иллюстрацией к одноименному уроку-семинару по алгебре и началам анализа, пр.

Методические рекомендации к урокам алгебры и начал анализа в 10 классе по теме: «Решение показательных уравнений и неравенств»

Материал содержит обобщение основных способов решения показательных уравнений и неравенств.

🔥 Видео

Как решать такие системы показательных уравненийСкачать

СИСТЕМЫ ПОКАЗАТЕЛЬНЫХ УРАВНЕНИЙ системы показательных неравенствСкачать

§14 Системы показательных уравнений и неравенствСкачать

Это просто! Как решать Показательные Неравенства?Скачать

Показательные и логарифмические уравнения. Вебинар | МатематикаСкачать

Показательные неравенства и их системы. Вебинар | МатематикаСкачать

10 класс. Алгебра. Системы показательных уравнений.Скачать

Показательные уравнения. Практическая часть. 11 класс.Скачать

Как решать Показательные Уравнения? (часть 2)Скачать

11 класс, 13 урок, Показательные неравенстваСкачать

Системы показательных уравнений и неравенств. 10 - 11 классСкачать

системы показательных уравнений и неравенствСкачать

Математика. 11-класс. Урок 4. Система показательных уравненийСкачать

Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать