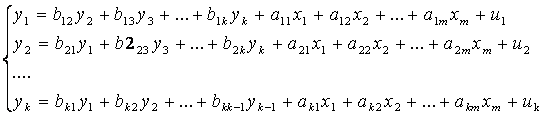Системы одновременных уравнений в эконометрике

Пример . Рассмотрим модель зависимости общей величины расходов на питание от располагаемого личного дохода (х) и цены продуктов питания (р):у = а₀ + а₁х + а₂р + ε. Определим класс модели и вид переменных модели: регрессионная модель с одним уравнением; эндогенная переменная — расходы на питание, экзогенные переменные — располагаемый личный доход и цена продуктов питания.

Принципиальные сложности применения систем эконометрических уравнений связаны с ошибками спецификации модели.

Система уравнений в эконометрических исследованиях может быть построена по-разному. Выделяют следующие 3 вида систем уравнений.

1. Система независимых уравнений, когда каждая зависимая переменная (y ) рассматривается как функция только от предопределенных переменных (х):
   
2. Система рекурсивных уравнений, когда в каждом последующем уравнении системы зависимая переменная представляет функцию от зависимых и предопределенных переменных предшествующих уравнений:

От структурной формы легко перейти к так называемой приведенной форме модели. Число уравнений в приведенной форме равно числу эндогенных переменных модели. В каждом уравнении приведенной формы эндогенная переменная выражается через все предопределенные переменные модели:

Так как правая часть каждого из уравнений приведенной формы содержит только предопределенные переменные и остатки, а левая часть только одну из эндогенных переменных, то такая система является системой независимых уравнений. Поэтому параметры каждого из уравнений системы в приведенной форме можно определить независимо обычным МНК.
Зная оценки этих приведенных коэффициентов можно определить параметры структурной формы модели. Но не всегда, а только если модель является идентифицируемой.

Видео:Эконометрия_л9Скачать

Проблема идентификации

Количество структурных и приведенных коэффициентов одинаково в модели идентифицируемой.

Видео:Система уравнений с двумя эндогенными переменнымиСкачать

Правила идентификации

Ранг данной матрицы равен 1, что меньше К-1=2, следовательно, 1-ое уравнение модели неидентифицированно.
Составим матрицу А для 2-ого уравнения системы. Во 2-ом уравнении отсутствуют переменные y₃, x₂, х₃:
y₃ x ₂ x₃
b₁₃ a ₁₃ 0 — в 1-ом уравнении
1 a₃₂ a₃₃ — в 3-ем уравнении
Ранг данной матрицы равен 2, что равно К-1=2, следовательно, 2-ое уравнение модели точно идентифицированно.
Составим матрицу А для 3-его уравнения системы. В 3-ем уравнении отсутствуют переменные y₁, x₂:
y ₁ x ₂
1 a₁₂ — в 1-ом уравнении
b₂₁ 0 — во 2-ом уравнении
Ранг данной матрицы равен 1, что меньше К-1=2, следовательно, 3-е уравнение модели неидентифицированно.

Сделаем выводы: 1-ое и 3-е уравнения системы неидентифицированны (т.к. не выполняются достаточные условия идентификации, а в случае 1-ого уравнения и необходимое условие также). 2-ое уравнение системы сверхидентифицированно. Следовательно, система в целом является неидентифицируемой.
Для оценки параметров 2-ого уравнения можно применить двухшаговый МНК. Параметры 1-ого и 3-его уравнений определить по коэффициентам приведенной формы нельзя. Поэтому модель должна быть модифицирована.

Видео:Системы одновременных эконометрических уравненийСкачать

Система одновременных эконометрических уравнений

Вы будете перенаправлены на Автор24

Видео:Двухшаговый метод наименьших квадратов в парной регрессииСкачать

Общие сведения о системе одновременных эконометрических уравнений

Система одновременных экономических уравнений – это совокупность уравнений, которые позволяют исследователям установить наличие и степень связи (взаимозависимости) между эконометрическими переменными.

Выделяют две группы экономических переменных, из которых образуют эконометрические уравнения:

• эндогенные переменные, чьи значения определяют в результате функционирования изучаемой экономической системы (эндогенные переменные зависят как от экзогенных, так и от других эндогенных переменных);
• экзогенные переменные, чьи значения задаются извне (т.е. определяются вне эконометрической модели) и являются основой для определения значений эндогенных переменных (экзогенные переменные являются независимыми).

Функционирование сложных экономических систем может быть объяснено благодаря построению изолированных уравнений регрессии и измерению на их основе тесноты связи между переменными. Однако истинное влияние отдельных признаков на вариацию результирующей переменной не может быть описано одним отдельно взятым уравнением регрессии. В связи с этим в изучении экономических процессов важное значение приобрело структурирование связей между системой переменных.

В качестве примера системы одновременных эконометрических уравнений можно привести простейшую макроэкономическую (кейнсианскую) модель, которая состоит из двух уравнений:

В данной модели эндогенными переменными являются C (расходы на потребление) и Y (доход), а экзогенной переменной – I (инвестиции). b представляет собой коэффициент, который выражает предельную склонность к потреблению.

Видео:Эконометрика. Линейная парная регрессияСкачать

Характеристика структурной и приведенной форм системы уравнений

Данная система от всех других систем уравнения отличается наличием определенной структурной формы эконометрической модели. Это форма предполагает, что в правых и левых частях разных уравнений системы находятся одни и те же экономические переменные. Структурная форма системы одновременных эконометрических уравнений в случае переноса всех эндогенных переменных в левую часть может быть представлено в следующем матричном виде: YA = XB + E.

Готовые работы на аналогичную тему

Кроме структурной также выделяют приведенную (прогнозную) форму системы. По сути она есть представление системы, в котором эндогенные переменные выражены через экзогенные, то есть в каждом уравнении имеется только одна эндогенная переменная. Тогда она выглядит так: Y = XП + U.

Приведенную форму системы всегда можно получить, если задана структурная форма. Однако обратное действие не всегда возможно, а если оно и возможно, то не всегда получается однозначный результат.

Если через коэффициенты приведенной формы можно выразить коэффициенты структурного уравнения, то оно называется идентифицируемым (в противном случае оно – неидентифицируемое). Точная индентифицируемость свойственна ситуации, когда способ подобного выражения является единственным. Если же их несколько, то говорят о сверхидентифицируемости.

Чтобы имела место идентифицируемость, требуется выполнение такого необходимого условия, как непревышение количества переменных правой части уравнения над количеством всех экзогенных переменных системы. Формулировка этого условия может отличаться. Так, часто говорят: количество экзогенных переменных, которые исключены из данного уравнения, должно быть не меньше количества эндогенных переменных, которые включены в уравнение, за вычетом единицы.

Также выделяют условие, достаточное для признания идентифицируемости системы. Оно заключается в том, чтобы общее число эндогенных переменных системы за вычетом единицы не превышало ранг матрицы, который составлен из коэффициентов (в других уравнениях) при переменных, отсутствующих в данном уравнении.

Видео:Системы эконометрических уравненийСкачать

Методы оценки систем одновременных эконометрических уравнений

Для того, чтобы оценить представленные в структурной форме уравнения системы, нецелесообразно непосредственно применять обычный метод наименьших квадратов. Это связано с тем, что подобное применение нарушит важнейшее условие регрессионного анализа — экзогенность (предопределенность, независимость) факторов. Тогда будут получены смещённые и несостоятельные оценки параметров.

Поэтому системы одновременных эконометрических уравнений оценивают посредством применения следующих методов:

• косвенный метод наименьших квадратов – подстановка в аналитическое выражение зависимости структурных коэффициентов от их приведённых оценок, которые получают в результате применения обычного метода наименьших квадратов;
• двухшаговый метод наименьших квадратов – оценивание сначала зависимости эндогенных переменных от всех экзогенных (первый шаг), а затем – структурной формы модели, в которой эндогенные переменные заменены на их оценки, полученные на первом шаге (второй шаг);
• трехшаговый метод наименьших квадратов – предыдущий метод дополняется третьим шагом, с помощью которого оценивают ковариационную матрицу вектора случайных ошибок системы уравнений;
• методы максимального правдоподобия – использование всей информации об ограничениях на приведённую форму эконометрической модели.

Видео:Эконометрика. Неделя 1. Суть метода наименьших квадратов.Скачать

Системы эконометрических уравнений

Видео:Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

7. Системы эконометрических уравнений

Видео:Коэффициент детерминации. Основы эконометрикиСкачать

7.1. Виды систем регрессионных уравнений

Любая экономическая система – это сложная система с множеством входов, выходов и сложной структурой взаимосвязей показателей, характеризующих деятельность этой системы. Поэтому для описания механизма функционирования таких систем обычно изолированных уравнений регрессии недостаточно.

Практически изменение какого-либо показателя в экономической системе, как правило, вызывает изменение целого ряда других. Так изменение производительности труда влияет на затраты труда, а, следовательно на себестоимость, прибыль, рентабельность производства и пр.

Все это вызывает потребность использования при описании сложных экономических явлений и процессов систем взаимосвязанных регрессионных уравнений и тождеств. Особенно актуальна необходимость в применении таких систем при моделировании на макроуровне, так как макроэкономические показатели, являясь обобщающими показателями состояния экономики, чаще всего взаимозависимы. Например, при построении модели национальной экономики необходимо рассмотреть уравнения, описывающие потребление, инвестиции, прирост капиталовложений, воспроизводство трудовых ресурсов, производство продукта и пр.

Переменные, входящие в систему уравнений подразделяют на экзогенные, эндогенные и лаговые (эндогенные переменные, влияние которых характеризуется некоторым запаздыванием, временным лагом ).

Экзогенные и лаговые переменные называют предопределенными, т. е. определенными заранее.

Классификация переменных на эндогенные и экзогенные зависит от принятой теоретической концепции модели. Экономические показатели могут выступать в одних моделях как эндогенные, а в других как экзогенные переменные. Внеэкономические переменные (например, климатические условия, социальное положение, пол, возраст) входят в систему только как экзогенные переменные. В качестве экзогенных переменных могут рассматриваться значения эндогенных переменных за предшествующий период времени (лаговые переменные).

Рассмотрим типы систем эконометрических уравнений.

1. Система независимых регрессионных уравнений (внешне не связанных)

В данном случае каждая зависимая переменная рассматривается как функция некоторого е набора факторов.

. (7.1)

Набор факторов в уравнениях (1) может варьировать. Каждое уравнение системы независимых уравнений может рассматриваться самостоятельно, а его параметры могут быть найдены на основе традиционного метода наименьших квадратов (МНК).

2. Система рекурсивных уравнений

В таких системах в одном из уравнений содержится единственная зависимая переменная , которая в следующем уравнении присутствует в качестве факторной переменной. В третье уравнение эти эндогенные переменные из предыдущих уравнений могут быть включены как факторные и т. д.

(7.2)

В данной системе каждое последующее уравнение наряду с факторными переменными включает в качестве факторов все зависимые переменные предшествующих уравнений. Каждое уравнение этой системы может рассматриваться самостоятельно, и его параметры определяются методом наименьших квадратов (МНК).

3. Система взаимозависимых (одновременных) уравнений

Наибольшее распространение в эконометрических исследованиях получила система взаимозависимых уравнений. В ней одни и те же зависимые (эндогенные) переменные в одних уравнениях входят в левую часть (т. е. выступают в роли результативных признаков), а в других уравнениях – в правую часть системы (т. е. выступают в качестве факторных переменных). Система взаимозависимых уравнений получила название системы совместных, одновременных уравнений. Тем самым подчеркивается, что в системе одни и те же переменные одновременно рассматриваются как зависимые в одних уравнениях и как независимые в других. В эконометрике эта система уравнений также называется структурной формой модели (СФМ).

Система одновременных уравнений в структурной форме и при отсутствии лаговых переменных может быть записана:

(7.3)

Кроме регрессионных уравнений (они называются также поведенческими уравнениями) модель может содержать тождества, которые представляют собой алгебраические соотношения между эндогенными переменными. Тождества позволяют исключать некоторые эндогенные переменные и рассматривать систему регрессионных уравнений меньшей размерности Параметры модели в структурной форме называют ее структурными коэффициентами

Система одновременных уравнений в структурной форме позволяет увидеть влияние изменений любой экзогенной переменной на значения эндогенной переменной. Целесообразно в качестве экзогенных переменных выбирать такие переменные, которые могут быть объектом регулирования. Меняя их и управляя ими, можно заранее иметь целевые значения эндогенных переменных.

В отличие от предыдущих систем каждое уравнение системы одновременных уравнений не может рассматриваться самостоятельно, и для нахождения его параметров традиционный МНК неприменим, т. к. нарушаются предпосылки, лежащие в основе МНК (например, предпосылка о некоррелированности факторных переменных с остатками). Эндогенные переменные являются случайными величинами, зависящими от . В том случае, когда эндогенная переменная входит в некоторое уравнение как факторная происходит нарушение названной предпосылки МНК. Таким образом, для нахождения структурных коэффициентов традиционный МНК неприменим. С этой целью используются специальные приемы оценивания.

Видео:Эконометрика Линейная регрессия и корреляцияСкачать

7.2. Приведенная форма модели

Для определения структурных коэффициентов на основе структурной модели формируют приведенную форму модели.

Приведенная форма модели представляет собой систему линейных функций эндогенных переменных от экзогенных:

(7.4)

где – коэффициенты приведенной формы модели, – случайные остатки для приведенной формы.

По своему виду приведенная форма модели ничем не отличается от системы независимых уравнений, параметры которой оцениваются традиционным МНК. Применяя МНК, можно оценить , а затем оценить значения эндогенных переменных через экзогенные.

Можно показать, что коэффициенты приведенной формы модели представляют собой нелинейные функции коэффициентов структурной формы модели. Рассмотрим структурную модель с двумя эндогенными переменными.

. (7.5)

Запишем соответствующую приведенную форму модели:

. (7.6)

Выразим коэффициенты приведенной формы модели через коэффициенты структурной модели.

Из первого уравнения (7.5) можно выразить (ради упрощения опускаем случайную величину): .

Подставим во второе уравнение (7.5):

(7.7)

Выразим из (7.7) : .

Поступая аналогично со вторым уравнением системы (7.5), получим

, т. е. система (7.5) принимает вид:

Таким образом, коэффициенты приведенной формы модели выражаются через коэффициенты структурной формы следующим образом:

Следует заметить, что приведенная форма модели хотя и позволяет получить значения эндогенных переменных через значения экзогенных, но аналитически она уступает структурной форме модели, так как в ней отсутствуют взаимосвязи между эндогенными переменными.

Видео:Что такое метод инструментальных переменных ?Скачать

7.3. Проблема идентификации

При правильной спецификации модели задача идентификация системы уравнений сводится к корректной и однозначной оценке ее коэффициентов. Непосредственная оценка коэффициентов уравнения возможна лишь в системах внешне не связанных уравнений, для которых выполняются основные предпосылки построения регрессионной модели, в частности, условие некоррелированности факторных переменных с остатками.

В рекурсивных системах всегда возможно избавление от проблемы коррелированности остатков с факторными переменными путем подстановки в качестве значений факторных переменных не фактических, а модельных значений эндогенных переменных, выступающих в качестве факторных переменных. Процесс идентификации осуществляется следующим образом:

1. Идентифицируется уравнение, в котором в качестве факторных не содержатся эндогенные переменные. Находится расчетное значение эндогенной переменной этого уравнения.

2. Рассматривается следующее уравнение, в котором в качестве факторной включена эндогенная переменная, найденная на предыдущем шаге. Модельные (расчетные) значения этой эндогенной переменной обеспечивают возможность идентификации этого уравнения и т. д.

В системе уравнений в приведенной форме проблема коррелированности факторных переменных с отклонениями не возникает, так как в каждом уравнении в качестве факторных переменных используются лишь предопределенные переменные. Таким образом, при выполнении других предпосылок рекурсивная система всегда идентифицируема.

При рассмотрении системы одновременных уравнений возникает проблема идентификации.

Идентификация в данном случае означает определение возможности однозначного пересчета коэффициентов системы в приведенной форме в структурные коэффициенты.

Структурная модель (7.3) в полном виде содержит параметров, которые необходимо определить. Приведенная форма модели в полном виде содержит параметров. Следовательно, для определения неизвестных параметров структурной модели можно составить уравнений. Такие системы являются неопределенными и параметры структурной модели в общем случае не могут быть однозначно определены.

Чтобы получить единственно возможное решение необходимо предположить, что некоторые из структурных коэффициентов модели ввиду слабой их взаимосвязи с эндогенной переменной из левой части системы равны нулю. Тем самым уменьшится число структурных коэффициентов модели. Уменьшение числа структурных коэффициентов модели возможно и другими путями: например, путем приравнивания некоторых коэффициентов друг к другу, т. е. путем предположений, что их воздействие на формируемую эндогенную переменную одинаково и пр.

С позиции идентифицируемости структурные модели можно подразделить на три вида:

Модель идентифицируема, если все структурные ее коэффициенты определяются однозначно, единственным образом по коэффициентам приведенной формы модели, т. е. если число параметров структурной модели равно числу параметров приведенной формы модели.

Модель неидентифицируема, если число коэффициентов приведенной модели меньше числа структурных коэффициентов, и в результате структурные коэффициенты не могут быть оценены через коэффициенты приведенной формы модели.

Модель сверхидентифицируема, если число коэффициентов приведенной модели больше числа структурных коэффициентов. В этом случае на основе коэффициентов приведенной формы можно получить два или более значений одного структурного коэффициента. Сверхидентифицируемая модель в отличие от неидентифицируемой модели практически решаема, но требует для этого специальных методов нахождения параметров.

Чтобы определить тип структурной модели необходимо каждое ее уравнение проверить на идентифицируемость.

Модель считается идентифицируемой, если каждое уравнение системы идентифицируемо. Если хотя бы одно из уравнений системы неидентифицируемо, то и вся модель считается неидентифицируемой. Сверхидентифицируемая модель кроме идентифицируемых содержит хотя бы одно сверхидентифицируемое уравнение.

Видео:Эконометрика. Множественная регрессия и корреляция.Скачать

7.4. Условия идентифицируемости уравнений структурной модели

1. Необходимое условие идентифицируемости

Чтобы уравнение было идентифицируемо, необходимо, чтобы число предопределенных переменных, отсутствующих в данном уравнении, но присутствующих в системе, было равно числу эндогенных переменных в данном уравнении без одного.

Введем следующие обозначения:

М – число предопределенных переменных в модели;

m— число предопределенных переменных в данном уравнении;

— число эндогенных переменных в модели;

— число эндогенных переменных в данном уравнении;

Обозначим число экзогенных (предопределенных) переменных, которые содержатся в системе, но не входят в данное уравнение через , .

Тогда условие идентифицируемости каждого уравнения модели может быть записано в виде следующего счетного правила:

Для оценки параметров структурной модели система должна быть идентифицируема или сверхидентифицируема.

Рассмотренное счетное правило отражает необходимое, но недостаточное условие идентификации.

Достаточное условие идентификации

Уравнение идентифицируемо, если по отсутствующим в нем переменным (эндогенным и экзогенным) можно из коэффициентов при них в других уравнениях системы получить матрицу, определитель которой не равен нулю, а ранг матрицы не меньше, чем число эндогенных переменных в системе без одного.

Целесообразность проверки условия идентификации модели через определитель матрицы коэффициентов, отсутствующих в данном уравнении, но присутствующих в других, объясняется тем, что возможна ситуация, когда для каждого уравнения системы выполнено счетное правило, а определитель матрицы названных коэффициентов равен нулю. В этом случае соблюдается лишь необходимое, но не достаточное условие идентификации.

В эконометрических моделях часто наряду с уравнениями, параметры которых должны быть статистически оценены, используются балансовые тождества переменных, коэффициенты при которых равны . В этом случае, хотя само тождество и не требует проверки на идентификацию, ибо коэффициенты при переменных в тождестве известны, в проверке на идентификацию структурных уравнений системы тождества участвуют..

Изучается модель (одна из версий модели Кейнса):

(7.8)

где – потребление в период ; – ВВП в период ; — ВВП в период (); – валовые инвестиции в период ; – государственные расходы в период .

Первое уравнение – функция потребления, второе уравнение – функция инвестиций, третье уравнение –тождество ВВП. Модель представляет собой систему одновременных уравнений. Проверим каждое ее уравнение на идентификацию.

Модель включает три эндогенные переменные и две предопределенные переменные (одна экзогенная переменная – и одна лаговая переменная –).

Проверим необходимое условие идентификации для каждого из уравнений модели.

тождество, не подлежит проверке

Например, первое уравнение содержит две эндогенные переменные и и одну предопределенную переменную .

Таким образом, ; D=2-1=1. Условие условие выполняется, т. е. уравнение идентифицируемо.

Проверим для каждого уравнения достаточное условие идентификации. Для этого составим матрицу коэффициентов при переменных модели.

В соответствии с достаточным условием идентификации ранг матрицы коэффициентов при переменных, не входящих в исследуемое уравнение, должен быть равен числу эндогенных переменных модели без одного.

Первое уравнение: матрица коэффициентов при переменных, не входящих в уравнение, имеет вид:. Ее определитель не равен нулю, поэтому ранг матрицы равен 2, т. е равняется числу эндогенных переменных без одного. Достаточное условие идентификации выполняется.

Второе уравнение: матрица коэффициентов при переменных, не входящих в уравнение, имеет вид: . Ранг данной матрицы равен 2, так как существут определитель второго порядка не равный нулю:. Следовательно, достаточное условие идентификации для данного уравнения также выполняется Но в соответствии с необходимым условием считаем это уравнение сверхидентифицируемым.

Таким образом, эта система уравнений является сверхидентифицируемой.

Видео:Системы уравнений Тема3 С истемы ур-й в которых одно ур-е 1ой степени а другие 2ой и более высокой.Скачать

7.5. Методы оценки параметров структурной формы модели

Коэффициенты структурной модели могут быть оценены разными способами в зависимости от вида системы одновременных уравнений. Наибольшее распространение в литературе получили следующие методы оценивания коэффициентов структурной модели:

1) косвенный метод наименьших квадратов;

2) двухшаговый метод наименьших квадратов;

3) трехшаговый метод наименьших квадратов;

4) метод максимального правдоподобия с полной информацией;

5) метод максимального правдоподобия при ограниченной информации.

Рассмотрим сущность некоторых из этих методов.

Косвенный метод наименьших квадратов (КМНК) применяется в случае точно идентифицируемой структурной модели. Процедура применения КМНК предполагает выполнение следующих этапов:

1. Для структурной модели строится приведенная форма модели.

2. Для каждого уравнения приведенной формы традиционным МНК оцениваются приведенные коэффициенты .

3. На основе коэффициентов приведенной формы находятся путем алгебраических преобразований параметры структурной модели.

Двухшаговый метод наименьших квадратов (ДМНК)

Если система сверхидентифицируема, то КМНК не используется, ибо он не дает однозначных оценок для параметров структурной модели. В этом случае могут использоваться разные методы оценивания, среди которых наиболее распространенным и простым является двухшаговый метод (ДМНК).

Основная идея ДМНК состоит в следующем:

· на основе приведенной формы модели получить для сверхидентифицируемого уравнения расчетные значения эндогенных переменных, содержащихся в правой части этого уравнения;

· подставляя найденные расчетные значения эндогенных переменных вместо фактических значений, можно применить обычный МНК к структурной форме сверхидентифицируемого уравнения.

Метод получил название двухшагового МНК, ибо дважды используется МНК:

· на первом шаге при определении параметров приведенной формы модели и нахождении на их основе оценок расчетных значений эндогенных переменных ; ;

· на втором шаге применительно к структурному сверхидентифицируемому уравнению, когда вместо фактических значений эндогенных переменных рассматриваются их расчетные значения, найденные на предыдущем шаге.

Сверхидентифицируемая структурная модель может быть двух типов:

· все уравнения системы сверхидентифицируемы;

· система содержит наряду со сверхидентифицируемыми точно идентифицируемые уравнения.

Если все уравнения системы сверхидентифицируемые, то для оценки структурных коэффициентов каждого уравнения используется ДМНК. Если в системе есть точно идентифицируемые уравнения, то структурные коэффициенты по ним можно найти на основе косвенного МНК. Двухшаговый метод, примененный к точно идентифицированным уравнениям дает такой же результат, что и косвенный МНК.

Продолжение примера 15.

Продолжим рассмотрение примера 15.

Система является сверхидентифицируемой: первое уравнение идентифицируемо, а второе уравнение сверхидентифицируемо. Поэтому для определения коэффициентов первого уравнения можно применить косвенный МНК, а для второго уравнении двухшаговый МНК.

Построим приведенную форму модели:

(7.9)

Исходные данные задачи (в млрд. руб.)

Предсказанное

Найдем параметры модели (7.9), применяя МНК к каждому уравнению,

используем « Пакет анализа» EXCEL):

(7.10)

Каждое уравнение статистически значимо (– статистики: =1302,55;

=281,956; =847,65). Коэффициенты детерминации свидетельствуют о хорошей связи между эндогенными и предопределенными переменными:=0,9977; =0,989; =0,996.

На основе уравнений модели (7.10) найдем структурные коэффициенты первого уравнения.

Выразим из третьего уравнения (7.10) переменную и подставим в первое уравнение. Получим первое структурное уравнение:

Так как второе уравнение сверхидентифицировано, то применим двухшаговый МНК. Найдем на основе третьего уравнения (7.10) расчетные значения переменной ( столбец «предсказанное » табл.23) и используем их для нахождения параметров второго структурного уравнения.

Получим: 4; .

В результате получим следующую систему структурных уравнений:

Трехшаговый метод наименьших квадратов (ТМНК)

Трехшаговый метод наименьших квадратов применяется для оценки параметров системы одновременных уравнений в целом. Сначала к каждому уравнению применяется двухшаговый метод с целью оценить коэффициенты и случайные остатки каждого уравнения. Затем строится ковариационная матрица остатков и проводится ее оценка. После этого для оценивания коэффициентов всей системы применяется обобщенный метод наименьших квадратов. ТМНК является достаточно эффективным, но требует существенно больших вычислительных затрат. Более подробное описание можно найти в работе[1][1]

Видео:Математика #1 | Корреляция и регрессияСкачать

7.6. Инструментальные переменные

Метод инструментальных переменных (МИП) применяется для оценивания уравнений, в которых регрессоры (факторы) коррелируют со свободными членами. Коррелированность между факторными переменными и случайными ошибками может быть вызвана разными причинами:

· пропущенными переменными, которые находятся в корреляционной связи с факторными переменными;

· ошибками измерений факторных переменных;

· включением лагированной зависимой переменной при наличии автокоррелированности ошибок. В этом случае лаговые переменные скорее всего будут коррелировать с ошибками;

· одновременные взаимосвязи между переменными (эндогенность переменных, включенных в правые части регрессионных уравнений).

Именно это явление оказывается характерным для систем одновременных уравнений;

Если между факторными переменными и случайными остатками имеется корреляционная зависимость (,), то нарушаются условия классической модели и оценки параметров, найденные по МНК будут смещенными и не состоятельными.

Идея МИП заключается в том, чтобы подобрать новые переменные , которые бы тесно коррелировали с и не коррелировали со случайными остатками . Такие переменные называют инструментальными или просто инструментами). Включение их в модель обеспечивает состоятельность оценок МНК.

Набор переменных может включать факторные переменные, которые не коррелируют с остатками, а также другие внешние величины, не входящие в состав факторных переменных модели. Важно, чтобы число инструментов было не меньше, чем число независимых переменных.

Рассмотрим случай парной регрессии: . Предположим, что между факторными переменными и остатками имеется корреляционная зависимость, т. е. . Рассмотрим систему нормальных уравнений для линейной парной регрессии:

, (7.11)

тогда . (7.12)

Можно показать, что . Так как , оценка параметра будет смещенной и не состоятельной.

Предположим, что можно найти такую переменную , которая была бы коррелированна с ( ), но не коррелированна с ( ). Выберем эту переменную в качестве иструментальной переменной.

Заменим второе уравнение системы (7.11) на следующее: и рассмотрим систему:

. (7.13)

Решение системы (7.13) будет, очевидно, отличается от решения предыдущей системы. Обозначим новые оценки соответственно.

В этом случае оценка . (7.14)

Покажем, что она является несмещенной и состоятельной при условии, что при увеличивающемся числе наблюдений стремится к конечному, отличному от нуля пределу, который мы обозначим, как .

, здесь , так как – постоянная величина.

Тогда . (7.15)

Так как , а , то в больших выборках стремится к истинному значению .

Сравним (формула (7.14) с оценкой МНК (формула 7.12). Очевидно, что оценку , можно получить путем подстановки инструментальной переменной вместо в числителе и вместо одного (но не обоих) в знаменателе в формуле (7.12) для оценки .

Чем теснее корреляция между и Z, тем меньше будет их дисперсия и, следовательно, тем меньше будет дисперсия . Следовательно, если мы стоим перед выбором между несколькими возможными инструментальными переменными, то следует выбрать наиболее тесно коррелированную с , потому что при прочих равных условиях она даст наиболее эффективные оценки. Вместе с тем не рекомендуется использовать инструментальную переменную, имеющую функциональную зависимость с , даже если бы ее удалось найти, потому что тогда она автоматически оказалась бы коррелированной с остатками и оценки по-прежнему были бы не состоятельны.

Нетрудно понять, что метод оценивания с помощью инструментальных переменных является обобщением обычного метода наименьших квадратов.

Пусть — матрица значений инструментальных переменных размерности (), а — матрица значений факторных переменных размерности (),. Здесь— матрица факторных переменных, которые включены в состав инструментов, — инструменты, которые не входят в число факторных переменных. В этом случае матрица оценок параметров находится следующим образом:

, где , (7.16)

здесь , а метод ИП называют обобщенным методом инструментальных переменны (ОМИП).

Если число инструментальных переменных равняется числу факторных переменных (), то матрица ) будет квадратной размерности (). Метод ИП в этом случае называется простым, а оценки вычисляются следующим образом:

=

=[2] . (7.17)

Самая трудная проблема метода ИП – это поиск подходящих инструментов. Требуется, чтобы инструменты были тесно связаны с факторными переменными, но сами не были бы эндогенными переменными.

Решение этой проблемы зависит от конкретной ситуации. Например, это могут быть: лаговые значения факторных переменных; показатели, близкие по экономическому смыслу и приближенно отражающие рассматриваемую факторную переменную и пр.

Метод инструментальных переменных используется при оценке СОУ при использовании двухшагового МНК. В качестве инструментов здесь рассматриваются расчетные значения эндогенных переменных, найденные на первом шаге с использованием обычного МНК для приведенной системы уравнений.

Рассмотрим упрощенную кейнсианскую модель формирования доходов в закрытой экономике без государственного вмешательства:

(7.18)

где — представляют совокупный выпуск, объем потребления и объем инвестиций соответственно, . Здесь мы имеем случай одновременных взаимосвязей между переменными: в качестве одной из составляющих содержит ошибку модели, а так как зависит от , то также корреллирует с ошибками модели.

Первое уравнение идентифицируемо ( и матрица коэффициентов при переменных, не входящих в уравнение состоит из одного элемента 1, т. е. ее ранг равен 1, что равняется числу эндогенных переменных без одного). Следовательно выполняютя необходимое и достаточное условие идентифицируемости. Второе уравнение тождество, не подлежит проверке на идентификацию.

Рассмотрим следующие статистические данные:

📸 Видео

Эконометрика. Построение модели множественной регрессии в Excel.Скачать

Решение систем уравнений методом подстановкиСкачать

Парная регрессия: линейная зависимостьСкачать

9 класс, 11 урок, Методы решения систем уравненийСкачать

ЭконометрикаСкачать