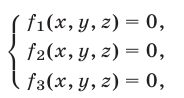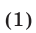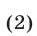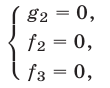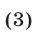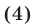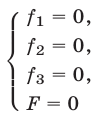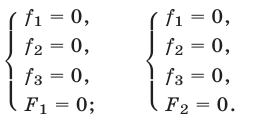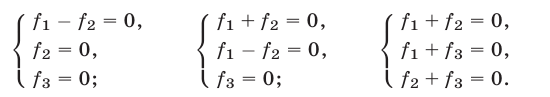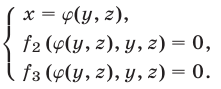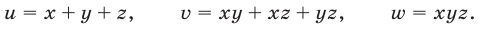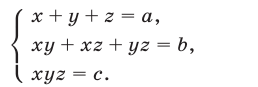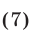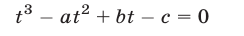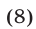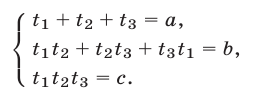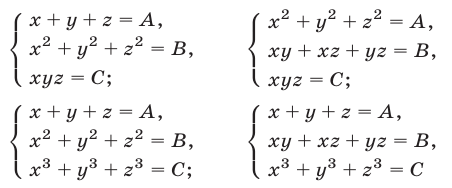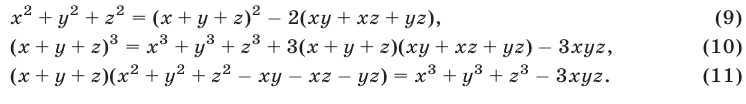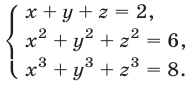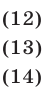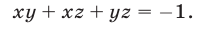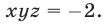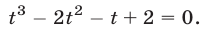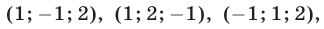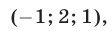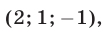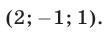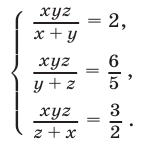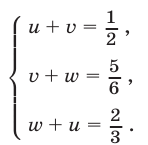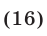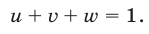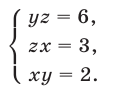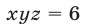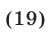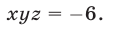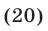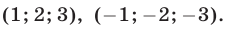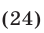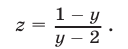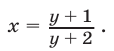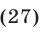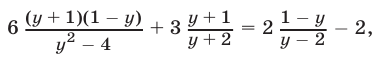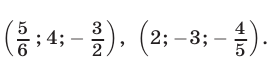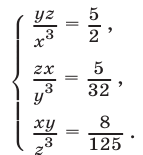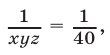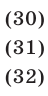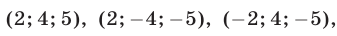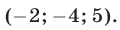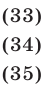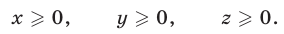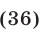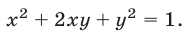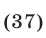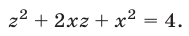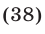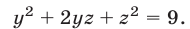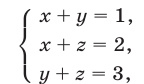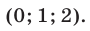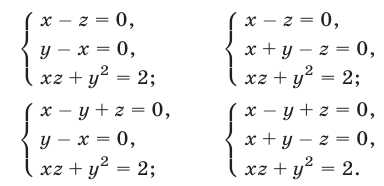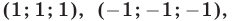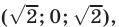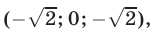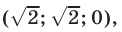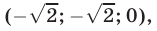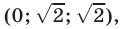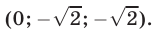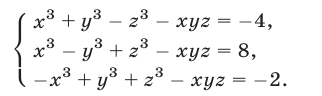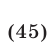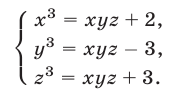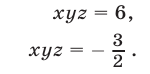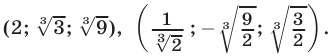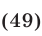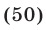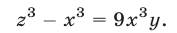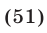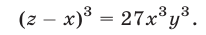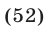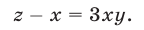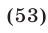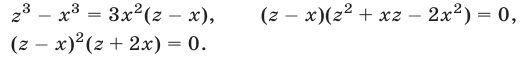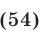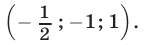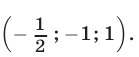Эти упражнения позволят проверить, как вы умеете решать системы линейных уравнений с 3-мя неизвестными.
Решение задач и упражнений лучший способ проверить свои знания и закрепить пройденный материал!
Для перехода к следующему заданию нажмите кнопку «Следующий пример».
Внимание. При переходе к новому заданию этот пример станет недоступным.
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
Видео:Алгоритм решения задач с помощью систем уравнений. Практическая часть. 9 класс.Скачать
Алгебраические системы с тремя неизвестными с примерами решения
Алгебраические системы с тремя неизвестными
Для систем с тремя неизвестными определения понятий равносильности и следствия, а также свойства преобразований систем формулируются аналогично тому, как это было сделано для систем с двумя неизвестными.
Будем рассматривать системы вида
где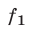 
, 
, 
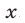
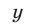
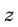
являются либо многочленами от 
, 
, 
, либо могут быть представлены в виде отношения многочленов.
Сформулируем для систем уравнений с тремя неизвестными следующие утверждения, которые могут оказаться полезными при решении систем.
1° Если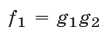 
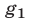
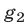
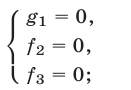
, где 
и 
—многочлены, то система (1) равносильна совокупности систем
и поэтому множество решений системы (1) в этом случае есть объединение множеств решений систем (2) и (3).
2°. Если уравнение
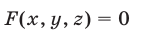
есть следствие системы (1), то система
равносильна системе (1), т. е. при добавлении к системе (1) еще одного уравнения (4), являющегося следствием этой системы, получается система, равносильная системе (1).
3°. Если уравнение (4) — следствие системы (1), причем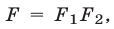 
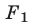
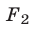
где 
и 
—многочлены, то система (1) равносильна совокупности систем
4°. Система (1) равносильна каждой из следующих систем:
5°. Если уравнение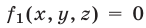 
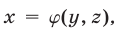
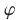
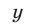
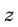
равносильно уравнению 
где 
— многочлен от и , то система (1) равносильна системе
Это утверждение лежит в основе метода исключения неизвестных: система (1) сводится к системе (5), (6) с двумя неизвестными.
Прежде чем переходить к примерам алгебраических систем с тремя неизвестными, отметим, что нет общих рецептов для нахождения решений систем. Каждый раз нужно учитывать конкретные особенности рассматриваемой системы. Можно дать только общий совет: решайте побольше задач.
Рассмотрим сначала системы с тремя неизвестными, которые сводятся к кубическим уравнениям.
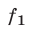
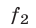
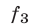
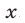
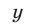
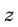
К таким системам относятся системы симметрических алгебраических уравнений, т.е. системы вида (1), где , , — многочлены, каждый из которых не меняется, если поменять местами любую пару из переменных , , .
В этом случае удобно ввести следующие переменные:
Простейший пример системы рассматриваемого вида — система
Система (7) и кубическое уравнение
связаны следующим образом.
Если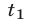 
, 
, 
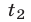
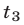
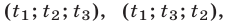
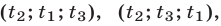
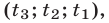
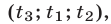
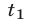
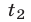
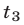
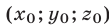
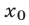
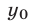
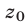
— корни уравнения (8), то система (7) имеет шесть решений: 
получаемых всевозможными перестановками трех чисел , , . Обратно, если 
решение системы (7), то 
, 
, 
— корни уравнения (8).
Доказательство этого утверждения основано на использовании формул Виета для корней уравнения (8):
Для сведения к системам (7) систем симметрических уравнений вида
можно использовать следующие тождества:
Примеры с решениями
Пример №186.
Решить систему уравнений
Решение:
Используя уравнения (12), (13) и тождество (9), получаем
Применяя формулу (11) и учитывая равенства (13)-(15), находим 
Следовательно, исходная система равносильна системе вида (7), в которой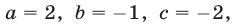 
, а уравнение (8) имеет вид
Корни этого уравнения — числа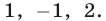 
Поэтому система имеет шесть решений, получаемых перестановкой чисел
Ответ. 
Обратимся теперь к системам с тремя неизвестными, которые не являются симметрическими.
Пример №187.
Решить систему уравнений
Решение:
Так как правые части уравнений отличны от нуля, то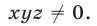 
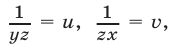
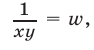
Полагая 
получаем систему линейных уравнений
Сложив уравнения системы (16), находим
Из (16) и (17) получаем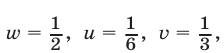 
т. е.
Перемножив почленно уравнения системы (18), которая равносильна исходной, имеем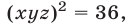 
откуда
Следовательно, исходная система равносильна совокупности систем (18), (19) и (18), (20), которые имеют решения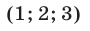 
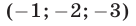
и 
соответственно.
Ответ. 
Пример №188.
Решить систему уравнений
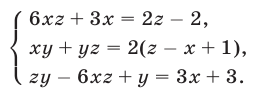
Решение:
Будем решать систему методом исключения неизвестных и сведением, в конечном счете, к одному уравнению с одним неизвестным. Складывая почленно уравнения (21) и (23), получаем
Так как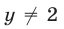 
на основании равенства (24), то из этого равенства следует, что
Запишем далее уравнение (22) в виде
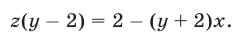
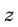
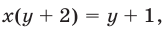
Исключив из уравнений (24) и (26), получаем 
откуда
Заметим, что система (27), (25), (21) равносильна системе (21)— (23). Подставляя выражения для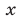 
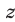
и 
из формул (27) и (25) в уравнение (21), получаем
или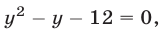 
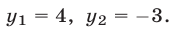
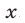
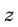
откуда 
Соответствующие значения и найдем по формулам (27) и (25).
Ответ. 
Пример №189.
Решить систему уравнений
Решение:
Перемножив уравнения системы (28), получаем 
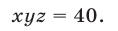
Уравнение (29) является следствием системы (28), которая равносильна системе
Уравнения (30), (31), (32) имеют решения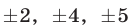 
соответственно. С учетом равенства (29) находим четыре решения системы (28).
Ответ. 
Пример №190.
Найти решения системы уравнений
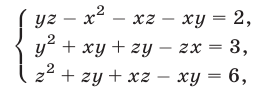
Решение:
Вычитая из уравнения (34) уравнение (33), получаем
Далее, вычитая из уравнения (35) уравнение (33), находим
Наконец, складывая уравнения (34) и (35), получаем
Система (37)-(39) равносильна системе (33)-(35), а при условии (36) — системе линейных уравнений
имеющей единственное решение
Ответ.
Пример №191.
Решить систему уравнений
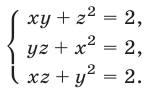
Решение:
Вычтем из уравнения (41) уравнение (40) и преобразуем полученное уравнение к виду
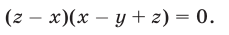
Выполнив ту же операцию с уравнениями (42) и (41), имеем
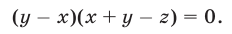
Система (43), (44), (42), равносильная системе (40)-(42), распадается на следующие четыре системы:
Полученные системы легко решаются методом исключения неизвестных. Объединив решения этих систем, найдем все решения исходной системы.
Ответ. 
Пример №192.
Решить систему уравнений
Решение:
Решим эту систему как линейную относительно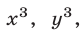 
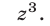
Для этого сложим попарно уравнения системы (45) и получим систему
Перемножив уравнения системы (46) и полагая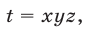 
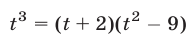
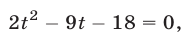
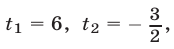
находим 
или 
откуда 
т. е.
Система (45) в силу утверждения 3° равносильна совокупности систем (46), (47) и (46), (48), каждая из которых имеет единственное решение.
Ответ.
Пример №193.
Решить систему уравнений
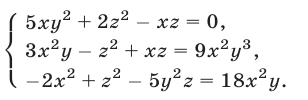
Решение:
Если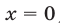 
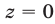
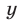
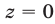
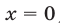
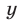
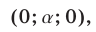
, то из системы (49) следует, что 
, а 
может принимать любые значения. Аналогично, если , то , — любое. Таким образом, система имеет бесконечное множество решений вида
Будем искать решения системы (49) такие, что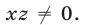 
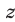
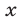
. Умножив первое уравнение системы (49) на , а третье — на 
и сложив результаты, получим
Прибавив к уравнению (51) второе уравнение системы (49), умноженное на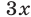 
:, находим
Каждое из уравнений (51), (52) является следствием системы (49).
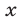
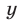
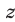
Так как , , — действительные числа (требуется найти действительные решения системы), то уравнение (52) равносильно уравнению
Исключая 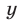из уравнений (53) и (51), получаем
Уравнения (53) и (54) являются следствиями системы (49), а уравнение (54) равносильно совокупности уравнений
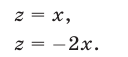
Из (55) и (53) следует, что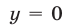 
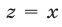
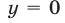
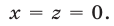
, а из системы (49) при 
и 
находим 
Полученное решение содержится среди решений (50).
Из (56) и (53) следует, что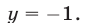 
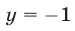
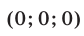
Подставляя 
в систему (49), находим решения 
и
Ответ.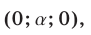 
— любое действительное число; 
Этот материал взят со страницы решения задач с примерами по всем темам предмета математика:
Возможно вам будут полезны эти страницы:
Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
Видео:Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать
Системы линейных уравнений с тремя переменными
Линейным уравнением называется уравнение вида:
В этом уравнении — неизвестные, а — действительные (или комплексные) числа. При этом называются коэффициентами уравнения, а — свободным членом.
Рассмотрим систему трех линейных уравнений с тремя неизвестными:
Из трех способов решения этих систем: графического, способа подстановки и способа сложения остается два последних способа. Графический способ уже не проходит, так как пришлось бы находить точку пересечения трех плоскостей. А это трудно изобразить.
Способ подстановки для трех уравнений похож на способ подстановки для двух уравнений с двумя неизвестными, только у этого способа на один шаг больше. Первое: выражаем одно из неизвестных из одного уравнения через два остальных неизвестных и подставляем это выражение в оставшиеся два уравнения. Эти оставшиеся два уравнения составляют систему из двух уравнений с двумя неизвестными. А дальше решаем эту полученную систему и находим два неизвестных, а затем, зная их, и третье неизвестное.
Пример 1 Решить систему уравнений: способом подстановки.
Выразим из первого уравнения через остальные неизвестные и свободный член. Найденное выражение подставим в остальные уравнения.
Далее, оставляя первое уравнение в покое, решаем систему из двух получившихся уравнений с неизвестными и (предварительно разделив обе части второго уравнения на ).
Получили единственное решение системы
Рассмотрим теперь способ сложения. Так же как и для двух уравнений с двумя неизвестными, нужно при помощи сложения уравнений добиться, чтобы одно из неизвестных пропало.Приведем пример.
Пример 2 Решить систему уравнений: способом сложения.
Постараемся получить два уравнения с двумя неизвестными. Избавимся от неизвестной . Для этого удвоенное первое уравнение сложим почленно с удвоенным вторым уравнением, а удвоенное второе уравнение прибавим к третьему уравнению:
Далее производим почленное сложение двух уравнений с двумя неизвестными, исключая неизвестную :
Из последнего уравнения системы находим 
. Подставляя найденное значение во второе уравнение, находим . Наконец из первого уравнения находим . Итак — единственное решение системы.
В заключении решим задачу, которая приводится к системе с тремя неизвестными.
Задача В трех урнах — шариков. В первой урне шариков больше чем во второй на столько, сколько шариков в третьей урне. Число шариков во второй урне относится к числу шариков в третьей урне как . Сколько шариков в каждой урне?
Обозначим число шариков в 1-й, 2-й и 3-й урнах через соответственно. Тогда первое условие задачи дает уравнение , второе условие — , а третье условие — . Запишем три полученные уравнения в систему, сделав предварительно третье уравнение линейным:
Складывая почленно первые два уравнения находим .Решаем систему из двух оставшихся уравнений:
Итак, в урнах соответственно и шариков.
Длины волн инфракрасного света достаточно велики, чтобы перемещаться сквозь облака, которые в противном случае блокировали бы наш обзор. Используя большие инфракра сные телескопы, астрономы смогли заглянуть в ядро нашей галактики. Большое количество звезд излучают часть своей электромагнитной энергии в виде видимого света, крошечной части спектра, к которой чувствительны наши глаза.
Так как длина волны коррелирует с энергией, цвет звезды говорит нам, насколько она горячая. Используя телескопы, чувствительные к различным диапазонам длин волн спектра, астрономы получают представление о широком круге объектов и явлений во вселенной.
Пример №1 Постройте центральную симметрию тетраэдра, относительно точки O, изображенных на рисунке 3.
Для построения такой центральной симметрии сначала проведем через все точки тетраэдра прямые, каждая из которых будет проходить через точку O. На них построим отрезки, удовлетворяющие условиям |AO|=|A?O|, |BO|=|B?O|, |CO|=|C?O|, |DO|=|D?O| Таким образом, и получим искомую симметрию (рис. 4).
В ряду разных механических движений особенным значением обладают колебания. Это движения и процессы, имеющие периодичность во времени.
В среде электромагнитных явлений также значительное место заняли электромагнитные колебания. В этих колебаниях заряды, токи, электрические и магнитные поля изменяются согласно периодическим законам.
Совет №1 Велосипедист, имеющий скорость 300 м/с, или идеальный газ, оказывающий давление 100 паскалей в большой тепловой машине — это странно.
Нужна помощь с курсовой или дипломной работой?
🎬 Видео
Система с тремя переменнымиСкачать
Метод Крамера за 3 минуты. Решение системы линейных уравнений - bezbotvyСкачать
Решение системы трех уравнений по формулам КрамераСкачать
Алгоритм решения задач с помощью систем уравнений. Практическая часть. 9 класс.Скачать
Урок по теме РЕШЕНИЕ ЗАДАЧ С ПОМОЩЬЮ СИСТЕМЫ УРАВНЕНИЙ 7 КЛАСССкачать
Решение системы уравнений методом Крамера.Скачать
Решение системы уравнений методом ГауссаСкачать
Матричный метод решения систем уравненийСкачать
Математика | Система уравнений на желтую звездочку (feat Золотой Медалист по бегу)Скачать
Математика без Ху!ни. Метод Гаусса.Скачать
Решение систем линейных алгебраических уравнений методом Крамера.Скачать
Задачи по химии. Использование системы уравнений 3Скачать
Система трёх уравнений. ЗадачаСкачать
Решение системы уравнений методом Крамера 2x2Скачать
Решение системы линейных уравнений графическим методом. 7 класс.Скачать
Решение систем уравнений методом подстановкиСкачать
Решение задач с помощью систем уравнений второй степени. Алгебра, 9 классСкачать
Решение системы уравнений с тремя неизвестными с помощью формул Крамера | Высшая математикаСкачать
