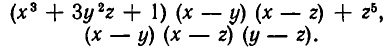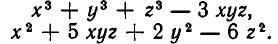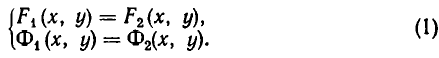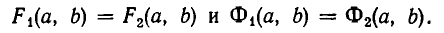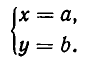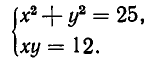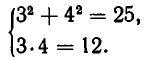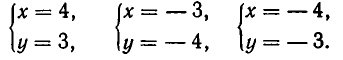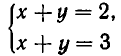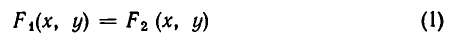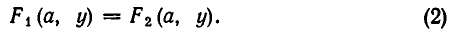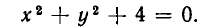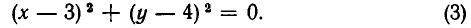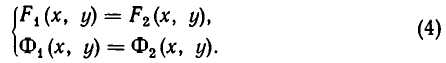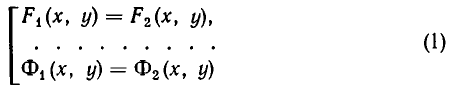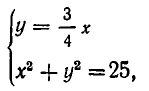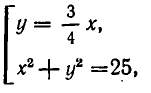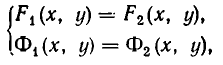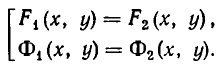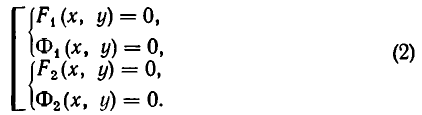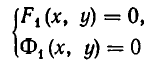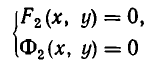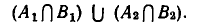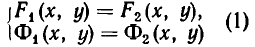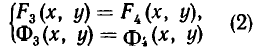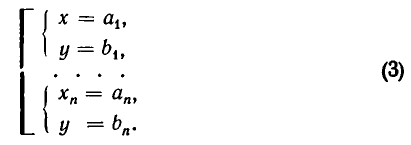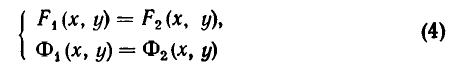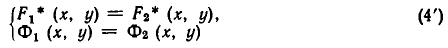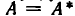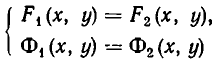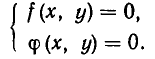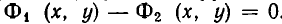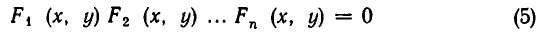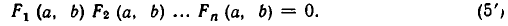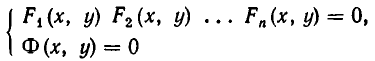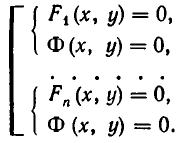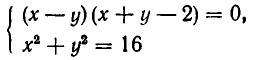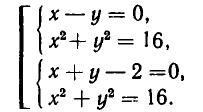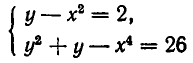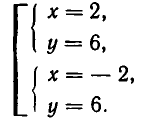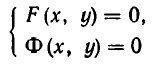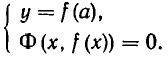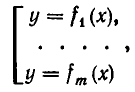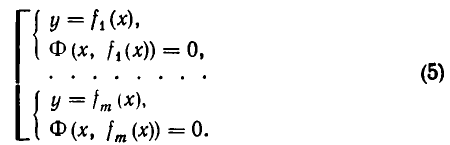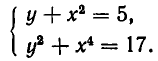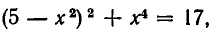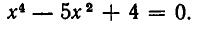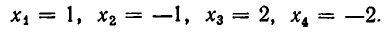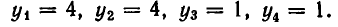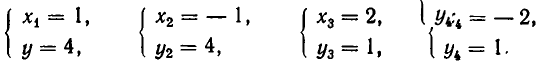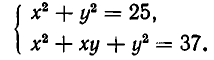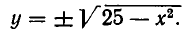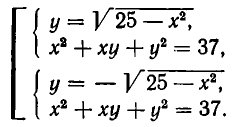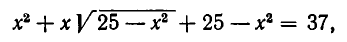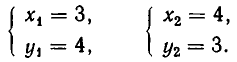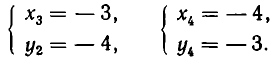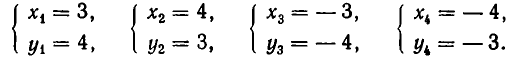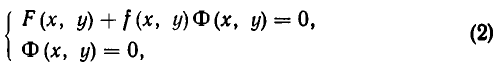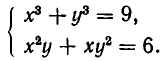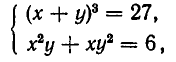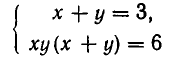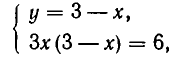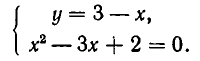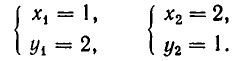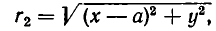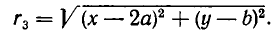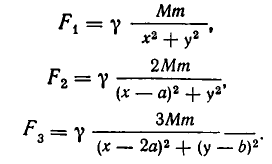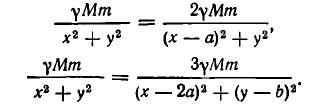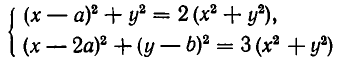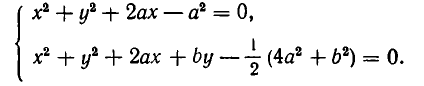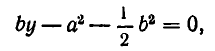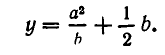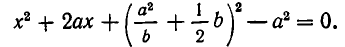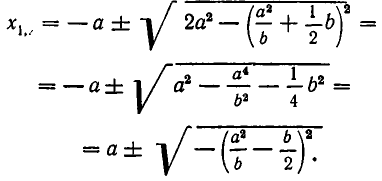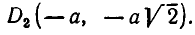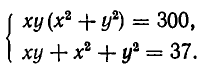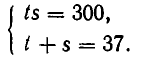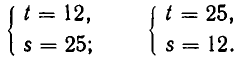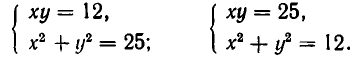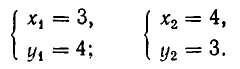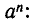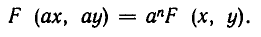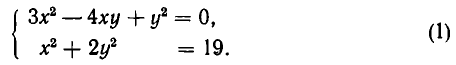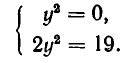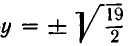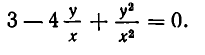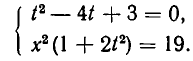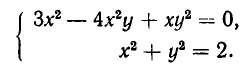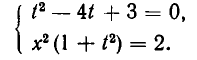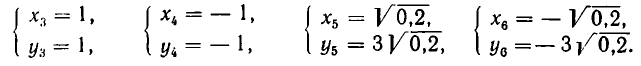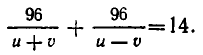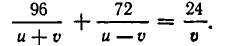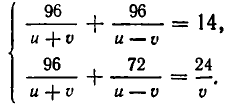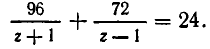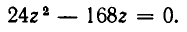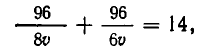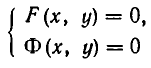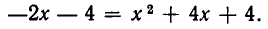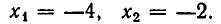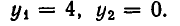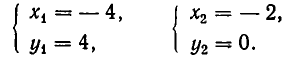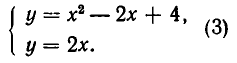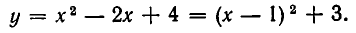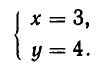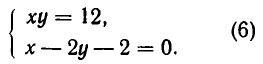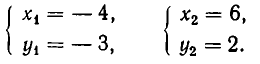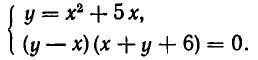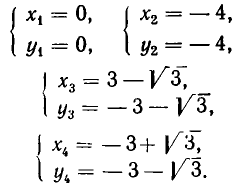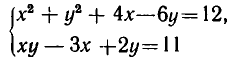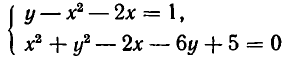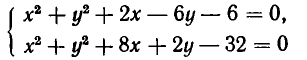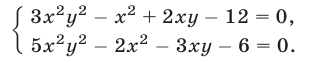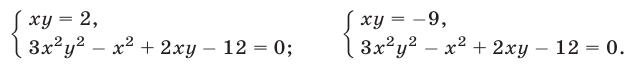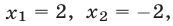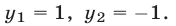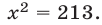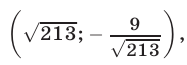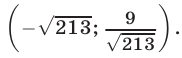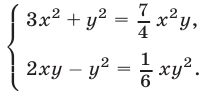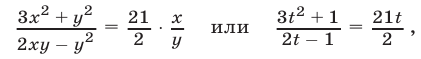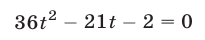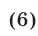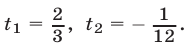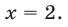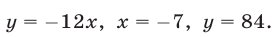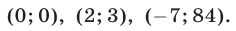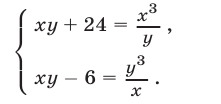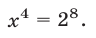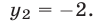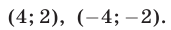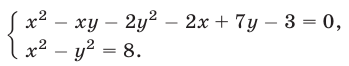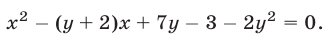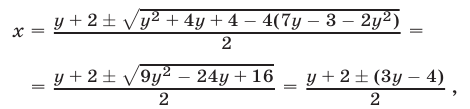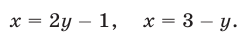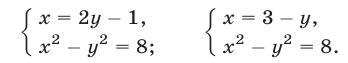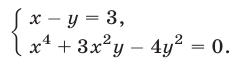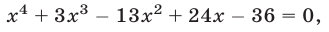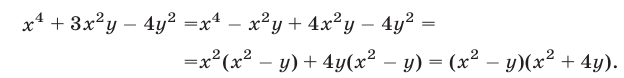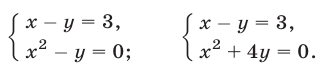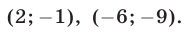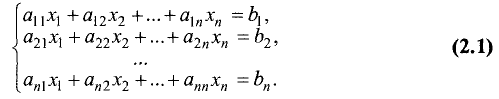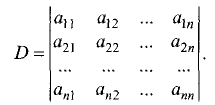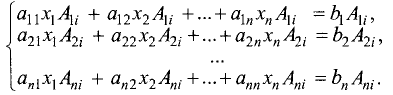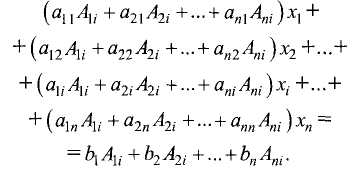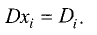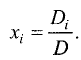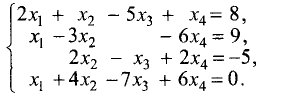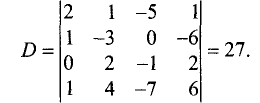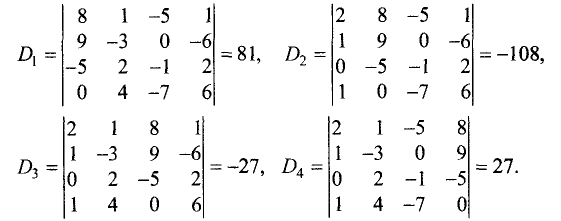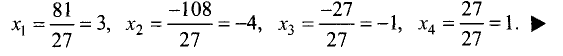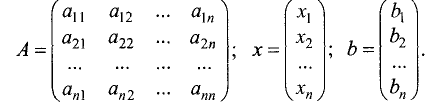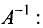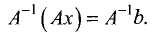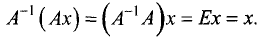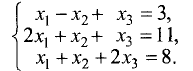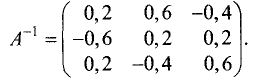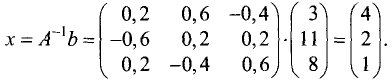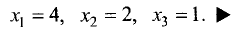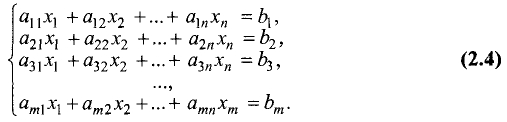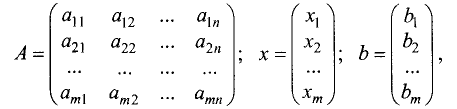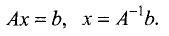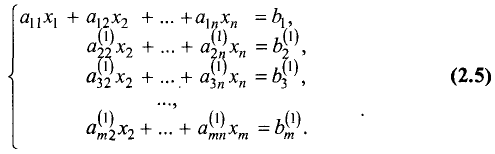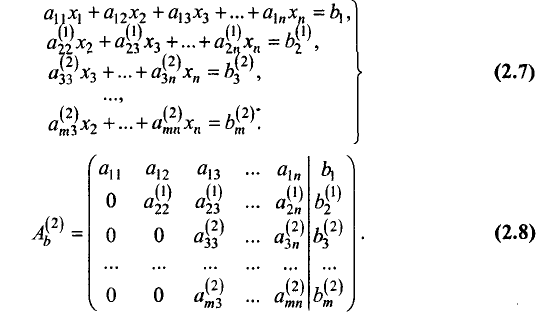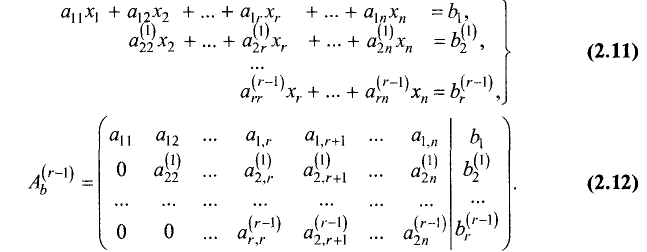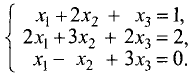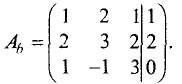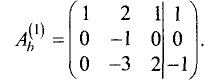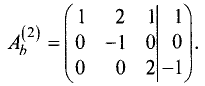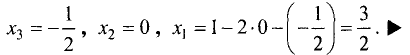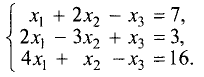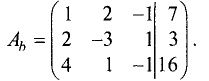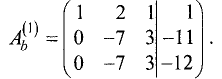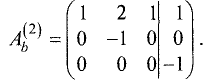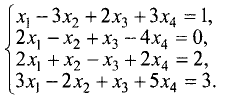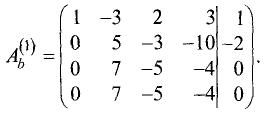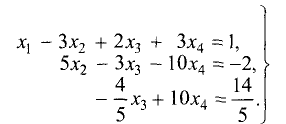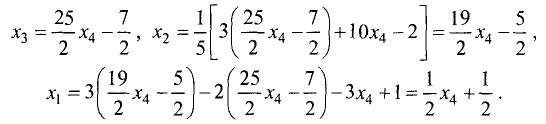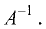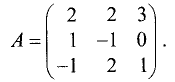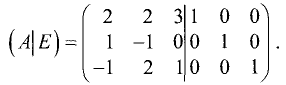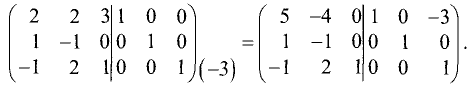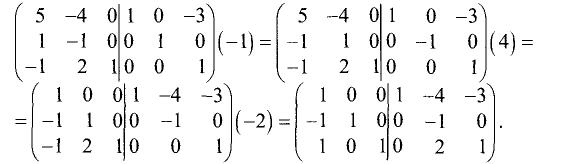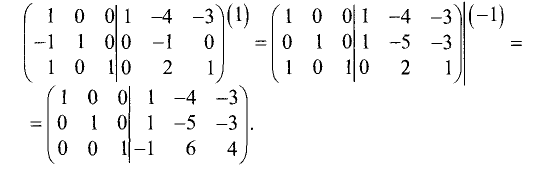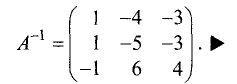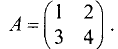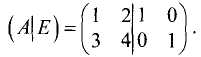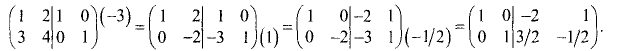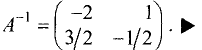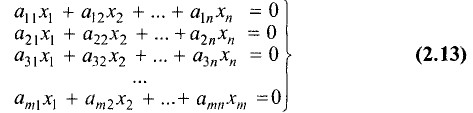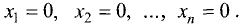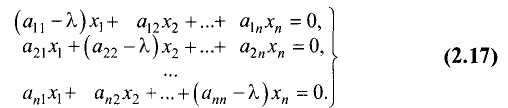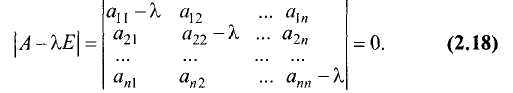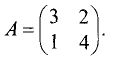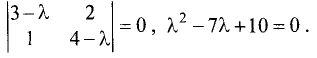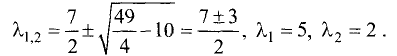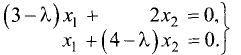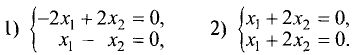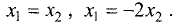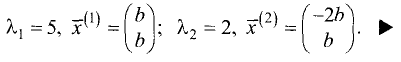Решение системы уравнений. Решением системы уравнений называют значение переменной, образующие оба уравнения системы в верные числовые равенства.
Замечание. Стандартное обозначение системы: $$ left< begin f_1 left( x right) = g_1 left( x right) \ f_2 left( x right) = g_2 left( x right) \ end right.$$
Пример: Решите уравнение $$ left( right)^2 + left( right)^2 = 0 $$
Решение. Слагаемые левой части данного уравнения неотрицательные, поэтому, равенство возможно, только если каждое слагаемое равно нулю: $$ left( right)^2 + left( right)^2 = 0 Leftrightarrow left< begin
left( right)^2 = 0 \ left( right)^2 = 0 \ end right. Leftrightarrow left< begin x = — 2 \ x = 5 \ end right. $$. Последние два равенства противоречат друг другу, следовательно система не имеет решения и называется несовместимой.
Совокупность уравнений. Задана совокупность двух уравнений с одной переменной, если требуется найти все такие значения переменной, при каждом из которых хотя бы одно из уравнений совокупности обращаются в верное числовое равенство.
Решение совокупности уравнений. Решением совокупности уравнений называют значение переменной, образующее хотя бы одно из уравнений совокупности в верное числовое равенство.
Пример: Решить уравнение $$ x^3 + x — 10 = 0$$
Решение. Разложим левую часть уравнения на множители $$ x^3 + x — 10 = left( right) + left( right) + left( right) = x^2 left( right) + 2xleft( right) + 5left( right) = left( right)left( right)$$. Получим уравнение $$ left( right)left( right) = 0 Leftrightarrow left[ begin
x — 2 = 0 \ x^2 + 2x + 5 = 0 \ end right. Leftrightarrow left[ begin x = 2 \ emptyset \ end right.$$. Второе уравнение совокупности не имеет решения, значит ответ x = 2
- Совокупности уравнений, неравенств, систем: определение, как решить
- Понятие совокупности
- Что такое решение совокупности
- Системы алгебраических уравнений в математике с примерами решения и образцами выполнения
- Системы уравнений
- Геометрический смысл решений уравнений и систем уравнений с двумя неизвестными
- Совокупность уравнений
- Равносильные системы уравнений
- Метод подстановки
- Метод алгебраического сложения уравнений
- Метод введения новых неизвестных
- Системы однородных уравнений
- Геометрическая интерпретация решения систем двух уравнений с двумя неизвестными
- Решение других типов систем алгебраических систем уравнений
- Решение системы алгебраических уравнений по правилу Крамера и методом обратной матрицы
- Общий вид системы линейных алгебраических уравнений
- Решение системы линейных алгебраических уравнений методом Гаусса
- Вычисление обратной матрицы методом Гаусса
- Система линейных однородных уравнений
- 🔍 Видео
Видео:Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

Совокупности уравнений, неравенств, систем: определение, как решить
Тема совокупностей уравнений и др. систем, как правило, в рамках школьного курса представлена скупо. В 10-11 классе она изучается совсем недолго. Мы считаем, что это неверный подход, поскольку совокупности — прекрасный способ оформления привычных решений при работе с неравенствами и уравнениями, поэтому в рамках статьи мы раскроем этот вопрос.
В данной статье мы сформулируем общее понятие совокупностей неравенств, уравнений и их систем, а также их комбинации. Кроме определений здесь, как обычно, есть решения задач, наглядно поясняющие тот или иной фрагмент текста.
Видео:Алгебраические уравнения. Способы решения. Понятия системы и совокупности уравнений. Разбор заданий.Скачать

Понятие совокупности
Для того, чтобы хорошо понимать, что такое совокупность уравнений, нужно вспомнить еще одно понятие из школьного курса алгебры — система уравнений (аналогично неравенствам). Тогда определения совокупности покажутся вам знакомыми и легко усвоятся.
Проанализировав несколько учебников, выберем наиболее удачное определение:
Совокупность уравнений представляет собой несколько уравнений, записанных друг под другом и объединенных квадратной скобкой. Значение этой записи таково: совокупность объединяет такие значения переменных, при которых хотя бы одно из входящих в нее уравнений превращается в верное равенство.
Сравним между собой понятие совокупности и понятие системы:
- Запись совокупности, как мы уже говорили выше, осуществляется с помощью квадратной скобки, а системы записываются с фигурной.
- Совокупность включает в себя множество решений, которые относятся хотя бы одному из уравнений, входящих в ее состав. Система объединяет решения, которые подходят для каждого уравнения.
Пример 1
Вот примеры совокупности уравнений:
x + 1 = 0 , x 2 — 1 = — 8 x + y 2 + z 4 = 0 , x · y · z = 0 , z = 5
Иногда при записи совокупности можно обойтись и без квадратной скобки: так часто делают в школе. В таком случае уравнения можно просто указать через запятую. Для примера выше это может быть запись вида x + y 2 + z 4 = 0 , x · y · z = 0 , z = 5 .
Понятие совокупности неравенств формулируется схожим образом.
Совокупность неравенств представляет собой несколько неравенств, записанных друг под другом и объединенных квадратной скобкой. Она включает в себя решения, которые подходят хотя бы для одного из неравенств, входящих в состав совокупности.
Приведем пример такой записи:
x + 3 > 0 , 2 · x + 3 ≤ 0 , 5
Схожее определение для этого понятия упоминается в учебнике Мордковича.
Если необходимо, то можно указать, сколько уравнений (неравенств) входят в состав совокупности, а также сколько в ней участвует переменных. Вид уравнения (неравенства) также может быть внесен в запись при необходимости. Сформулируем название совокупности из примера: это совокупность 2-х неравенств с одной переменной, а ее составные части — это целые рациональные первой степени.
Сочетать в рамках одной совокупности можно не только записи одного вида. Так, имеет право на существование совокупность, состоящая из двух неравенств и одного уравнения, сочетание одного неравенства с системой уравнений, двух систем неравенств и др. Главная задача — сохранить неизменным основной смысл совокупности: в нее входят такие решения, которые подходят хотя бы для одной составляющей совокупности.
В качестве примера смешанных совокупностей приведем две:
x > 3 x 8 x — 5 x ≤ — 2 x 2 = 9 x 2 > 5 ( x — 6 ) · ( x — 8 ) = 0 x ≤ 3 x 2 + 2 · x — 8 > 0
Видео:Решение системы неравенствСкачать

Что такое решение совокупности
Решение — главная составляющая совокупности. Сформулируем, что же такое решения совокупности с разным количеством переменных.
Решение совокупности с одной переменной представляет собой значение этой переменной, которое является решением хотя бы одной составляющей совокупности (уравнения, неравенства).
Если мы возьмем совокупность уравнений, значит, его решение — это значение x , при котором хотя бы одно из уравнений, входящих в состав совокупности, обращается в верное равенство.
Возьмем неравенство x > 1 , x 2 ≥ 4 · x + 2 . Для него решением, например, будет тройка, т.к. она больше единицы, и, следовательно, она — верное решение для первого неравенства. А если мы возьмем ноль, то увидим, что ни к одному из неравенств он не подходит; значит, 0 в качестве решения совокупности мы рассматривать не можем , ведь запись вида 0 > 1 и x 2 ≥ 4 · x + 2 неверна.
Решение совокупности, в которую входит две, три и более переменных, — это две, три и более переменных, которые подходят в качестве решения хотя бы одному компоненту совокупности.
Возьмем еще один пример, посложнее. У нас есть совокупность:
x 2 + y 2 = 4 , x + y > 0 , x ≥ 3
Значения 3 и 0 будут верными решениями совокупности: они подходят в качестве верных значений в уравнения 2 и 3 ( 3 + 0 > 0 и 3 ≥ 3 — верно). А вот значения 2 и 1 не есть решение совокупности: ни к 1 , ни ко 2 , ни к 3 они не подойдут.
В некоторых учебниках можно встретить также понятия общего и частного решения совокупности; под частным при этом понимается одно решение, а под общим — их некое множество. Но более употребительно понятие просто решения совокупности, а о том, общее оно или частное, можно понять из контекста.
Также нужно отметить следующее: объединение решений всех компонентов совокупности также есть решение совокупности. Напомним, что решение системы представляет собой пересечение решений ее компонентов.
В продолжение темы мы советуем вам материал «Равносильные совокупности».
Видео:Система уравнений VS Система неравенств. ОГЭ по математике №9, 13| Математика TutorOnlineСкачать

Системы алгебраических уравнений в математике с примерами решения и образцами выполнения
Целые рациональные функции от нескольких переменных: В этой главе мы изучим системы уравнений от нескольких переменных. В основном мы будем рассматривать системы алгебраических уравнений, то есть уравнений, обе части которых являются целыми рациональными функциями от неизвестных. Понятие целой рациональной функции от нескольких переменных определяется точно так же, как и в случае одного переменного; исходным, как и тогда, будет служить понятие целого рационального выражения.
Алгебраическое выражение, получающееся из чисел и букв x, у, … , z с помощью операций сложения и умножения, называется целым рациональным выражением от х, у, …, z. Примерами целых рациональных выражений являются:
Как и в случае выражений от одного переменного, каждое целое рациональное выражение от нескольких переменных можно привести к каноническому виду. Речь идет о суммах одночленов, то есть о выражениях вида 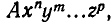
Правила действия над многочленами вытекают из основных законов алгебры.
Видео:Системы квадратных неравенств и их решение. 8 класс.Скачать

Системы уравнений
Рассмотрим некоторые общие вопросы теории систем уравнений. Для простоты ограничимся системами уравнений с двумя неизвестными, хотя основные результаты применимы и к системам уравнений с большим числом неизвестных.
Рассмотрим систему уравнений
Она выражает следующую задачу: найти все пары чисел (а, b) такие, что
Пары чисел (а, b), обладающие этим свойством, называют решениями системы (1). Если множество решений системы пусто, то система называется несовместной.
Тот факт, что пара (а, Ь) является решением системы уравнений с неизвестными х и у, записывается обычно в виде:
Например, пара чисел 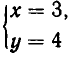
Помимо решения 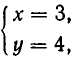
Позже мы увидим, что иных решений она не имеет.
Геометрический смысл решений уравнений и систем уравнений с двумя неизвестными
Возьмем любое уравнение относительно х и у:
и рассмотрим все точки М (х, у) некоторой плоскости, координаты которых удовлетворяют этому уравнению. Эти точки образуют не которое множество Г, и мы будем говорить, что уравнение (1) задает (или выражает) это множество. Обычно множество Г является некоторой линией. В этом случае уравнение (1) называют уравнением линии Г.
Чтобы найти точки линии 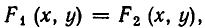
Может случиться, что это уравнение не имеет ни одного действительного корня. Тогда на линии нет точек с абсциссой х = а. Если же уравнение (2) имеет один или несколько корней, то каждому корню соответствует точка линии, имеющая абсциссу а.
Для некоторых уравнений на плоскости нет ни одной точки, координаты которых удовлетворяли бы этим уравнениям. Примером может служить
Ведь если х и у — действительные числа, то 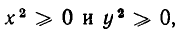
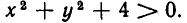
Так как 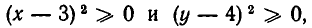
Однако такие случаи являются в некотором смысле исключи тельными, и мы ограничимся рассмотрением случаев, когда уравнение 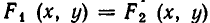
Перейдем теперь к выяснению геометрического смысла решений систем уравнений с двумя неизвестными. Возьмем такую систему:
Каждому из этих уравнений соответствует линия, координаты всех точек которой (и только этих точек!) удовлетворяют этому уравнению. Мы же ищем точки М (.х, у), координаты которых удовлетворяют обоим уравнениям. Ясно, что эти точки принадлежат обеим линиям, то есть являются точками их пересечения.
Итак, задача о решении системы уравнений равносильна зада че об отыскании точек пересечения соответствующих линий. Каждой точке пересечения линий соответствует решение системы.
Совокупность уравнений
образуют совокупность, если требуется найти все пары чисел х = а, у = b, удовлетворяющие хотя бы одному из уравнений (1). Все такие пары чисел (а, Ь) будем называть решениями совокупности (1). Геометрически решения совокупности (1) изображаются фигурой, образованной объединением всех кривых
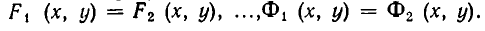
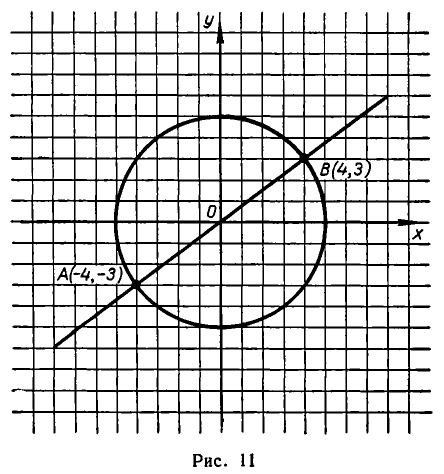
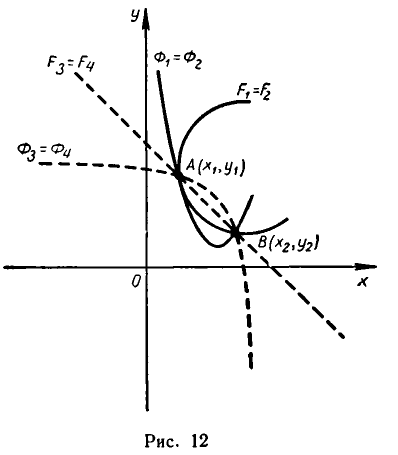
Например, возьмем уравнения 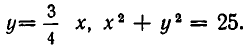
то решения будут изображаться точками пересечения прямой и окружности (то есть точками Л и В на рис. 11). Если же рассматривать эти уравнения как совокупность уравнений
то решение этой совокупности изображаются геометрической фигурой, получаемой объединением прямой и окружности.
Чтобы различать системы уравнений и совокупности уравнений, мы и стали обозначать систему уравнений так:
а совокупность уравнений так:
Можно говорить и о таком более сложном понятии, как совокупность систем уравнений. Например, возьмем такую запись:
Она означает, что надо найти решения системы уравнений
и найти решения системы уравнений
и объединить найденные решения.
Геометрически это изображается так: надо найти точки пересечения линий 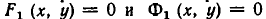
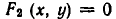
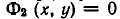
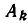
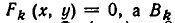
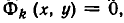
Равносильные системы уравнений
Две системы уравнений
называются равносильными, если всякое решение первой системы является решением второй, а всякое решение второй системы является решением первой.
В частности, любые две несовместные системы уравнений равносильны.
Геометрически это означает следующее: линии 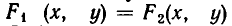
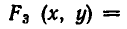
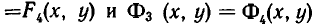
Процесс решения системы уравнений заключается в том, что ее последовательно заменяют равносильными ей системами уравнений (или совокупностями систем уравнений) до тех пор, пока не придут к совокупности вида:
Эта совокупность и дает решения заданной системы уравнений.
При решении систем уравнений чаще всего используются следующие теоремы о равносильности.
Теорема:
заменить любое из уравнений равносильным ему уравнением, то получим систему, равносильную первоначальной.
Доказательство:
Пусть 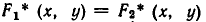
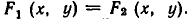
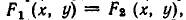
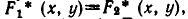
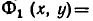
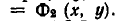
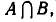
является пересечение 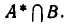
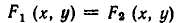
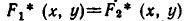
а значит, и 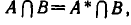
Из этой теоремы вытекает такое
Следствие:
Каждая система уравнений
равносильна некоторой системе уравнений вида
В самом деле, уравнение 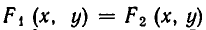
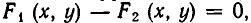
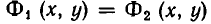
Теорема:
Если функции 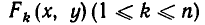
равносильно совокупности уравнений
Доказательство:
Если 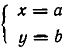
Но произведение нескольких чисел может равняться нулю тогда и только тогда, когда равен нулю хотя бы один из сомножителей. Поэтому для некоторого 
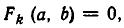
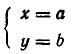
Обратно, если 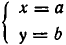
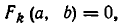
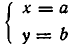
Из теоремы 2 вытекает.
Следствие:
равносильна совокупности систем уравнений
Например, система уравнений
равносильна совокупности систем
Это следствие позволяет сводить системы к совокупностям более простых систем
Метод подстановки
Теоремы п. 5 относятся по сути дела к отдельным уравнениям, а не к системе в целом. При решении систем уравнений применяются также преобразования уравнений, затрагивающие не одно уравнение, а несколько. Например, для решения системы
мы находим из первого уравнения выражение у через 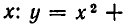
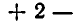
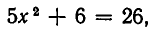
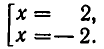
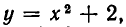
Метод, которым была решена эта система, называется методом подстановки. Он позволяет сводить решение системы уравнений с двумя неизвестными к более простой задаче — решению одного уравнения с одним неизвестным. Выясним теперь, на чем же основан метод подстановки. Для этого докажем следующую теорему.
Теорема:
равносильна системе уравнений
Доказательство:
Пусть 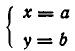
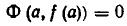
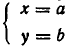
Обратно, пусть 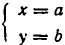
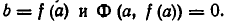
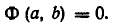
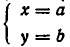
Тем самым равносильность систем уравнений (1) и (2) доказана.
Из теорем 2 и 3 вытекает
Следствие:
Если уравнение F (х, у)=0 равносильно уравнению 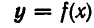
равносильна системе уравнений
Мы уже говорили, что теорема 3 лежит в основе метода решения систем уравнений с двумя неизвестными, называемого методом исключения неизвестных. Он состоит в следующем.
Пусть задана система уравнений
Выразим из первого уравнения системы у через х, то есть заменим уравнение F(х, у)= 0 равносильным ему уравнением у = f(х). Полученное выражение для у подставим во второе уравнение, то есть заменим систему уравнений (1) равносильной ей системой
Уравнение Ф (х,f(x)) является уже уравнением с одним неизвестным. Решая его, получим корни 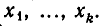

Часто приходится заменять уравнение F(х,у)= 0 не одним уравнением вида у = f(х), а совокупностью
таких уравнений. Тогда и система (1) заменяется совокупностью систем
Из каждой системы этой совокупности получаем описанным выше методом решения заданной системы, после чего объединяем их.
Примеры:
- Решить систему уравнений:
Из первого уравнения системы находим 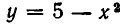
или, после упрощения,
Корнями этого биквадратного уравнения являются числа:
Им соответствуют значения:
Значит, решения заданной системы уравнений имеют вид:
2. Решить систему уравнений:
Из первого уравнения системы получаем:
Значит, нам надо решить совокупность двух систем уравнений:
Делая в первой системе подстановку, получаем:
или 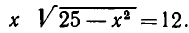
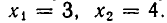
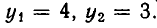
Точно так же доказывается, что вторая система имеет решения:
Следовательно, заданная система имеет решения:
Метод алгебраического сложения уравнений
Кроме метода подстановки, при решении систем алгебраических уравнений применяется метод алгебраического сложения. Он основан на следующей теореме.
Теорема:
Если к одному из уравнений системы
прибавить другое уравнение, умноженное на любой множитель f(x, y), определенный при всех допустимых значениях неизвестных, а второе уравнение оставим неизменным, то получится система уравнений, равносильная исходной.
Таким образом, система (1) равносильна системе
где множитель f(х,у) определен при всех допустимых значениях неизвестных.
Доказательство:
Пусть х = а, у = b — решение системы (1), то есть F(а, b)=0 и Ф(а, b)= 0.
Умножим обе части равенства Ф(а, b)=0 на число f(а, b) и прибавим к равенству F (а, b)= 0. Мы получим, что F(а, b)+(а, b) Ф(а,b)= 0, а потому х =а, у = b удовлетворяет и системе (2).
Точно так же доказывается, что любое решение системы уравнений (2) удовлетворяет системе уравнений (1). Значит, системы уравнений (1) и (2) равносильны.
Из теоремы 4 вытекает такое
Следствие:
Если к одному из уравнений системы (1) прибавить другое уравнение системы, умноженное на любое число, а второе уравнение оставить неизменным, то получим систему, равносильную первоначальной.
Покажем, как применяются эти утверждения для решения систем уравнений. Пусть дана система уравнений:
Здесь нецелесообразно выражать х через у или у через х, так как мы получили бы довольно сложное иррациональное уравнение. Поэтому поступим иначе. Прибавим к первому уравнению системы второе уравнение, умноженное на 3. В силу формулы для куба суммы получим систему уравнений:
равносильную заданной. Эта система равносильна системе:
(поскольку уравнение 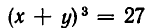
А теперь выразим из первого уравнения у через х и подставим во второе уравнение. Мы получим:
Из второго уравнения находим: 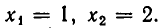
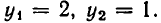
Задача:
Массы трех планет 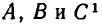
система координат. Координаты планет равны соответственно A(0,0), В (а, 0), С (2а, b). При каком значении b на плоскости существует точка, в которой притяжение ко всем трем планетам одинаково?
Решение:
По закону всемирного тяготения сила притяжения между телами с массами 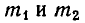
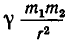
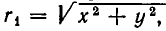
а до точки С (b, с) равно
Поэтому силы, с которыми тело массы m, находящееся в точке D, притягивается к планетам, равны
По условию задачи должны выполняться условия 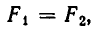
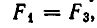
После сокращения обоих уравнений на 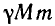
Вычтем первое уравнение из второго. Мы получим, что
Подставляя это значение у в первое уравнение, получаем для х квадратное уравнение
Из него находим:
Отсюда получаем, что х принимает действительные значения лишь в случае, когда 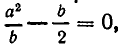
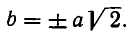
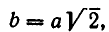
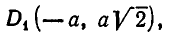
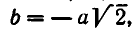
Метод введения новых неизвестных
Для решения многих систем оказывается удобно ввести вместо х и у новые неизвестные. Рассмотрим следующий пример:
Если положить 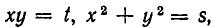
Решая эту систему, получаем, что
Так как 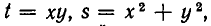
Решениями первой системы являются:
Вторая же система не имеет действительных решений.
Общего правила для выбора новых неизвестных не существует. Однако в некоторых случаях можно указать полезные правила.
Системы однородных уравнений
Назовем f (х, у) однородным многочленом относительно х и у степени n, если при замене х на ах и у на ау F (х, у) умножается на
Например, 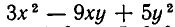
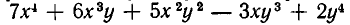
Пусть одно из уравнений системы имеет вид: F (х,у) = 0, где F (х, у)— однородный многочлен. Тогда решение системы сводится к решению двух уравнений, каждое из которых содержит лишь одно неизвестное. Покажем на примере, как это делается.
Пусть дана система уравнений:
Посмотрим сначала, есть ли у этого уравнения решения, для которых х =0. Подставляя х = 0 в оба уравнения системы, получаем систему уравнений:
Эта система несовместна, так как из первого уравнения получаем у = 0, а из второго —
Итак, система не имеет решений, для которых х = 0. Поэтому первое уравнение системы можно разделить на 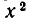
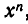
Положим у — tх. Мы придем к системе уравнений:
Корнями первого уравнения являются 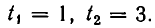
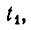
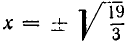
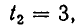
В следующем примере система имеет решения, для которых х = 0:
При х = 0 первое уравнение обращается в равенство 0=0, а второе принимает вид 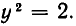
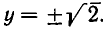
Другие решения получаются так же, как и в первом случае. Мы делим первое уравнение системы на 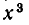
Из первого уравнения находим 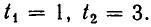
Задача:
От пристани А одновременно отправились вниз по течению катер и плот. Катер спустился вниз по течению на 96 км, затем повернул обратно и вернулся в А через 14 часов. Найти скорость катера в стоячей воде, если известно, что катер встретил плот на обратном пути на расстоянии 24 км от А.
Решение:
Сначала составим систему уравнений. В качестве неизвестных выберем скорость u катера в стоячей воде и скорость течения v. Тогда скорость катера при движении по течению равна u+v, а при движении против течения u-v. Значит, чтобы пройти вниз по течению 96 км, ему надо 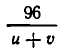
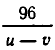
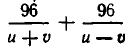
Чтобы получить второе уравнение, найдем, какое время затратил катер до встречи с плотом. Он прошел 96 км вниз по течению и 72 км против течения. На это он затратил 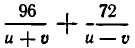
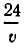
Мы получим систему уравнений:
При замене u на ut и v на vt обе части второго уравнения умножаются на 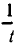
Освобождаясь от знаменателей, получим:
Так как 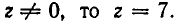
откуда v = 2 (км/ч). Поэтому u = 14 км/ч.
Геометрическая интерпретация решения систем двух уравнений с двумя неизвестными
Мы уже знаем, что решение системы двух уравнений с двумя неизвестными
геометрически истолковывается как отыскание точек пересечения двух линий. Этим можно воспользоваться для приближенного решения системы уравнений. Именно, если изобразить линии F(х, у) = 0 и Ф(х, у) = 0, мы сможем найти координаты точек пересечения этих линий и тем самым значения неизвестных. Поскольку линии чертятся лишь приближенно, мы получаем не точные, а приближенные значения решений системы. Тем не менее, решая графически систему, мы можем узнать, сколько она имеет решений, и, хотя бы грубо, найти приближенные значения этих решений.
При графическом решении систем уравнений мы сталкиваемся с различными кривыми. В курсе геометрии были выведены уравнения прямой, окружности, параболы, гиперболы и эллипса. В дальнейшем мы будем пользоваться этими кривыми.
Рассмотрим некоторые примеры систем уравнений.
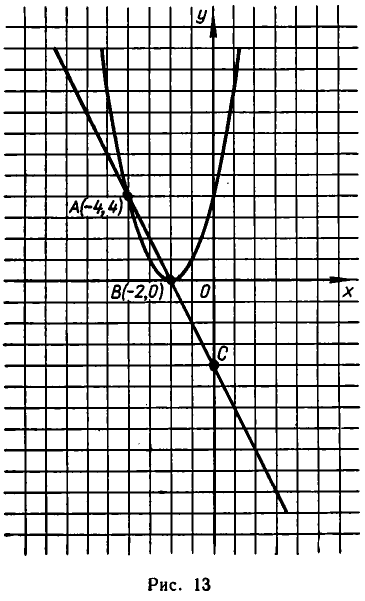
Пусть дана система
Выразив из уравнения (2) у через х и подставив в первое уравнение, получаем квадратное уравнение:
Подставив их во второе уравнение, получаем:
Итак, система имеет два решения:
Построим теперь линии, выражаемые уравнениями (1) и (2). Уравнение (1) — это уравнение параболы 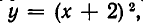
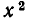
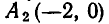
Парабола может иметь с прямой линией не две, а одну точку пересечения и даже не иметь ни одной точки пересечения.
Возьмем систему уравнений:
Ее единственное решение:
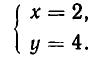
Из рис. 14 мы видим, что прямая у = 2х касается параболы
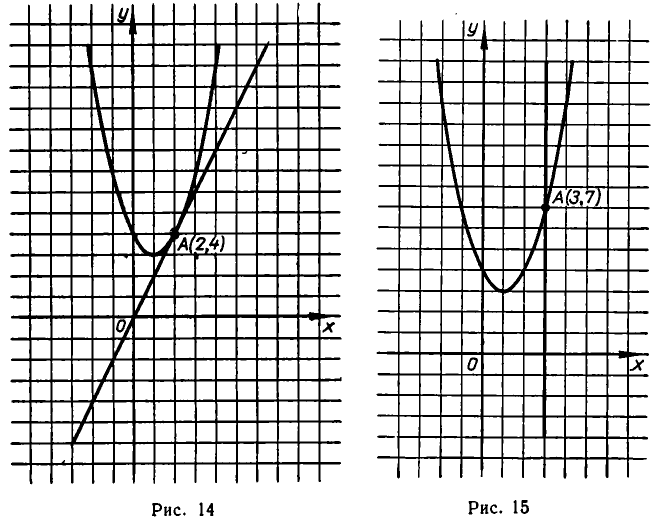
тоже имеет одно решение:
Но в этом случае прямая не касается параболы, а пересекает ее (см. рис. 15).
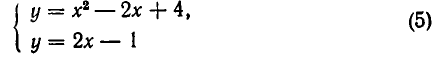
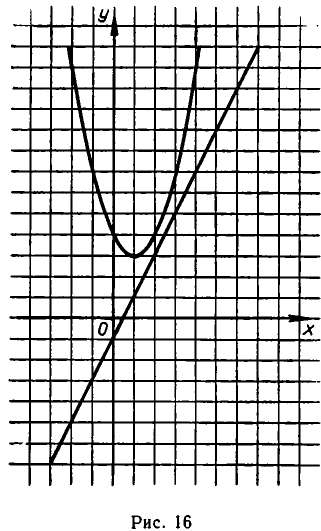
не имеет ни одного решения — здесь прямая и парабола не пересекаются (см. рис. 16).
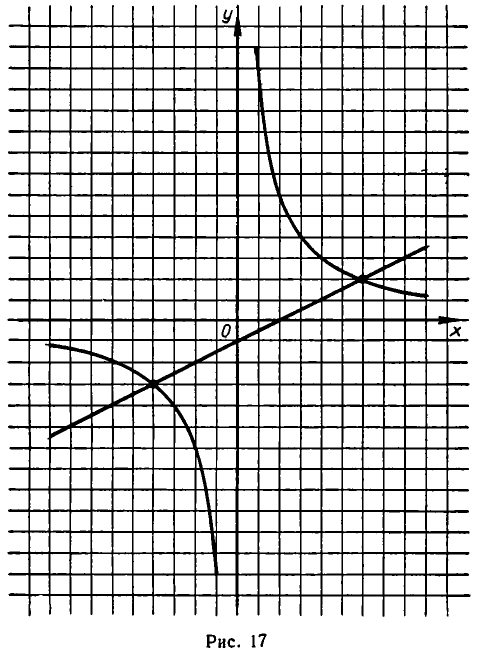
Теперь рассмотрим систему, геометрический смысл которой заключается в отыскании точек пересечения прямой и гиперболы. Пусть система имеет вид:
Решая ее способом подстановки, находим решения:
Эти же решения получаются графическим способом (см. рис. 17). Однако следует иметь в виду, что графический способ дает лишь приближенные значения корней и, решая систему (6) графически, мы не можем быть уверены, что решение имеет вид х = —4, у = —3, а не, например, х = —4,01, у = —2,99.
Как и в случае параболы, может случиться, что прямая имеет не две, а меньше общих точек с гиперболой.
Перейдем к системам, в которых оба уравнения имеют вторую степень. Можно доказать, что такие системы уравнений имеют не более четырех решений.
Вообще можно доказать, что система двух уравнений с двумя неизвестными такая, что первое уравнение имеет степень m, а второе — степень n, имеет не более mn решений.
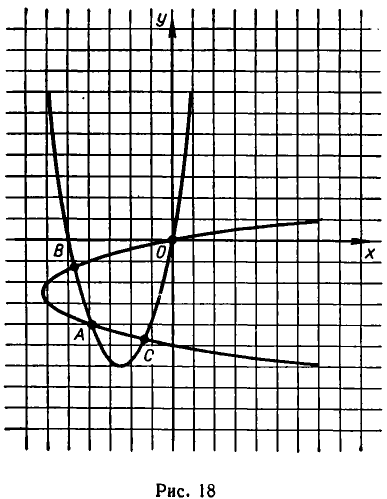
Рассмотрим, например, систему:
Первое из этих уравнений представляет параболу с осью, параллельной оси ординат, а второе — параболу с осью, параллельной оси абсцисс (см. рис. 18). Из рисунка видно, что эти параболы пересекаются в четырех точках. Чтобы найти координаты точек пересечения,
решим эту систему методом алгебраического сложения. Именно, вычтем из уравнения (8) уравнение (7). Мы получим равносильную систему уравнений:
Эта система равносильна совокупности систем:
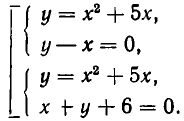
Обе системы этой совокупности решаются методом подстановки. Мы получаем при этом следующие решения заданной системы:
тоже имеет четыре решения. Она выражает задачу об отыскании точек пересечения окружности и гиперболы (см. рис. 19). Что бы решить эту систему, надо прибавить к первому уравнению удвоенное второе уравнение.
В некоторых случаях получается меньше чем четыре решения системы. Например, система
имеет два решения. Она выражает задачу об отыскании точек пересечения параболы и окружности (рис. 20).
Столько же решений имеет система
(пересечение двух окружностей) (рис. 21).
Видео:Решение системы линейных неравенств с одной переменной. 6 класс.Скачать
Решение других типов систем алгебраических систем уравнений
Пример:
Решить систему уравнений
Решение:
Из данной системы можно исключить 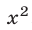
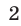
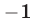
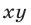
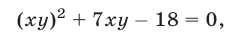
откуда 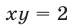
Система (1), (2), равносильная системе (1), (3), распадается на две системы:
Из первой системы находим
Из второй системы получаем
Ответ. 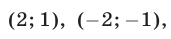
Пример:
Решить систему уравнений
Решение:
Если 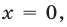
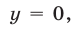
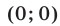
Пусть 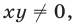
где 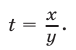
имеет корни
Заметим, что при 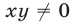
Если 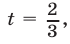
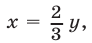
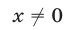
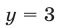
Если 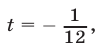
Ответ.
Пример:
Решить систему уравнений
Решение:
Допустимые значения 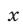
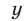
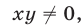
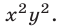
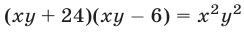
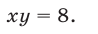
Так как обе части уравнений (7) и (8) отличны от нуля, то система (9), (7) равносильна системе (7), (8). Исключая у из системы (9), (7), получаем
Из (10) следует, что 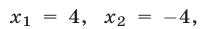
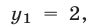
Ответ.
Пример:
Решить систему уравнений
Решение:
Запишем первое уравнение в виде
Решив это уравнение как квадратное относительно 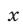
Таким образом, исходная система распадается на следующие две системы:
Пример:
Решить систему уравнений
Решение:
Исключив 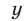
нахождение корней которого — совсем не простая задача. Более эффективный способ основан на разложении левой части уравнения (12) на множители:
Отсюда вытекает, что система (11), (12) распадается на следующие две системы:
Первая из этих систем не имеет действительных решений, а вторая имеет два решения.
Ответ.
Этот материал взят со страницы решения задач с примерами по всем темам предмета математика:
Возможно вам будут полезны эти страницы:
Видео:ПРОСТЕЙШИЙ метод решения систем квадратных неравенствСкачать

Решение системы алгебраических уравнений по правилу Крамера и методом обратной матрицы
Пусть дана система линейных уравнений, состоящая из n
линейных уравнений с n неизвестными:
Здесь 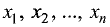
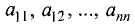
циенты при неизвестных, 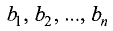
Определитель, состоящий из коэффициентов при неизвестных,
называется определителем системы.
Для рассматриваемого случая определитель системы имеет вид
Предположим, что этот определитель отличен от нуля. Пусть i —
любое число от 1 до n . Умножим обе части первого равенства
системы уравнений (2.1) на алгебраическое дополнение 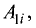
получающееся вычеркиванием первой строки и i-го столбца в определителе системы. Обе части второго равенства этой системы умножим на алгебраическое дополнение 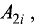
Сложим левые и правые части получившейся системы
уравнений, скомпоновав их следующим образом:
Коэффициентом при 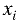
системы D. При всех остальных х коэффициенты будут равны нулю,
так как они являются суммой произведений всех элементов столбцов
определителя на алгебраические дополнения соответствующих
элементов другого столбца (п. 5 свойств определителей, § 1.9). Правая
часть равенства является определителем, полученным из
определителя системы D после замены в нем i-го столбца столбцом из
свободных членов системы уравнений. Обозначим этот определитель 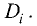
Так как 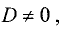
Этот метод решения системы линейных уравнений называется
правилом Крамера.
Правило Крамера. Пусть D — определитель системы п линейных
уравнений, состоящий из коэффициентов при неизвестных, a 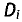
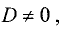
Пример:
Решить систему линейных уравнений:
Решение:
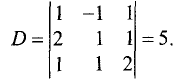
Определитель этой системы отличен от нуля:
После замены в этом определителе соответствующих столбцов
столбцом свободных членов получим
Решение системы уравнений:
Решить систему линейных уравнений можно, используя матричный метод. Для этих целей коэффициенты данной системы, неизвестные и свободные члены представим в виде матриц:
Тогда система линейньк уравнений в матричной форме имеет вид
Умножим слева эту матрицу на
Преобразуем левую часть равенства:
Таким образом, решение в матричной форме можно записать в виде
Пример:
Решить систему линейных уравнений:
Решение:
Определитель данной системы
Обратную матрицу находим по схеме, приведенной в § 1.11:
Находим матрицу решений:
Таким образом, система имеет следующее решение:
Видео:Система уравнений. Метод алгебраического сложенияСкачать

Общий вид системы линейных алгебраических уравнений
Систему из m линейных уравнений с n неизвестными, или систему m х n, можно записать в общем виде следующим образом:
Если так же, как и в предыдущем разделе, ввести обозначения
то система линейных уравнений в матричной форме и ее решение
примут вид
Решение системы линейных алгебраических уравнений методом Гаусса
Метод Гаусса состоит в последовательном исключении переменных. При этом на первом шаге из второго уравнения исключается 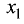
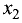
Шаг 1. Предположим, что коэффициент при 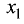
уравнении системы (2.4) 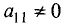
уравнений местами добьемся того, что 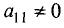
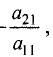
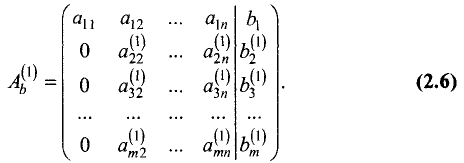
Умножим первое уравнение на 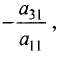
Для удобства записи обычно используют расширенную матрицу системы, отделяя в ней вертикальной чертой столбец свободных членов. После первого шага данная матрица принимает вид:
Шаг 2. Предположим, что коэффициент при 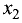
уравнении системы (2.5) 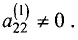
уравнений местами добьемся того, что 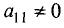
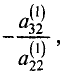
третьим уравнением системы (2.5) или матрицы (2.6) и результат
запишем в виде третьего уравнения системы (2.7) или матрицы
(2.8). Аналогично поступаем с остальными уравнениями системы:
Продолжая процесс последовательного исключения переменных, после (r-1)-го шага получим систему уравнений и расширенную матрицу:
Последние m-r уравнений в системе (2.9) для совместной
системы (2.4) являются тождествами: 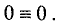
чисел 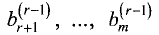
расширенная матрица (2.10) принимают вид
После отбрасывания уравнений, являющихся тождествами,
число оставшихся уравнений может быть либо равно числу
переменных r=n, либо меньше числа переменных. В первом случае
матрица имеет треугольный вид, а во втором — ступенчатый. Переход от системы уравнений (2.4) к равносильной ей системе (2.11)
называется прямым ходом метода Гаусса, а нахождение переменных из системы (2.11) — обратным ходом.
Пример:
Методом Гаусса решить систему уравнений
Решение:
Расширенная матрица этой системы имеет вид
Шаг 1. Расширенную матрицу первого шага получаем за счет
умножения первой строки на —2 и сложения результата со второй
строкой, а также за счет умножения первой строки на -1 и сложения
результата с третьей строкой:
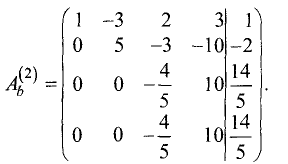
Ш а г 2. Расширенную матрицу первого шага получаем за счет
умножения второй строки на -3 и сложения результата с третьей строкой:
Эта матрица имеет треугольную форму и соответствует системе
линейных уравнений
Отсюда последовательно находим
Пример:
Методом Гаусса решить систему уравнений
Решение:
Расширенная матрица этой системы имеет вид
Ш а г 1. Расширенную матрицу первого шага получаем за счет
умножения первой строки на —2 и сложения результата со второй
строкой, а также за счет умножения первой строки на -4 и сложения результата с третьей строкой:
Ш а г 2. Расширенную матрицу первого шага получаем за счет
умножения второй строки на —1 и сложения результата с третьей строкой:
Уравнение,соответствующее третьей строке последней матрицы, противоречиво. Оно имеет вид 0 = -1. Следовательно, данная система несовместна. ►
Пример:
Методом Гаусса решить систему уравнений
Решение:
Расширенная матрица этой системы имеет вид
Ш а г 1. Первую строку последовательно умножаем на числа -2; —2;
-3 и складываем результат с соответствующими строками исходной
расширенной матрицы:
Ш а г 2. Умножаем вторую строку на 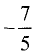
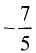
Шаг 3. Умножаем третью строку на -1.
После удаления последнего уравнения приведенная система
уравнений принимает вид
Из этой системы обратным ходом метода Гаусса находим
Так как 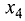
система имеет бесконечное множество решений. ►
Вычисление обратной матрицы методом Гаусса
Этот наиболее простой метод вычисления обратной матрицы
состоит в следующем. Пусть А — невырожденная матрица.
Припишем к ней справа единичную матрицу Е. Далее с помощью
элементарных преобразований над строками расширенной матрицы 
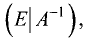
Пример:
Найти матрицу, обратную исходной:
Решение:
Составим расширенную матрицу:
Приведем левую половину этой матрицы к единичной матрице:
Последний столбец левой половины матрицы принял вид
последнего столбца единичной матрицы:
Последний и предпоследний столбцы левой половины матрицы
приняли вид последнего и предпоследнего столбцов единичной матрицы:
Правая половина этой расширенной матрицы является искомой
обратной матрицей, т.е.
Пример:
Найти матрицу, обратную исходной:
Решение:
Составим расширенную матрицу:
Приведем левую половину этой матрицы к единичной матрице:
Правая половина этой расширенной матрицы является искомой
обратной матрицей, т.е.
Видео:Система и совокупность. Как решать неравенстваСкачать

Система линейных однородных уравнений
Система m линейных уравнений с n переменными называется системой линейных однородных уравнений, если все ее свободные члены равны нулю.
Такая система имеет вид
Система линейных однородных уравнений всегда совместна, так
как она имеет, по крайней мере, нулевое (тривиальное) решение
Если система (2.13) имеет n линейных уравнений, а ее определитель отличен от нуля, то такая система имеет только нулевое решение. Это следует из правила Крамера. Ненулевое решение возможно для систем линейных однородных уравнений, у которых определитель равен нулю или m Собственные значения и собственные векторы матриц
Пусть матрица имеет порядок n или, что то же самое, размер n х n.
Вектор 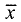
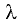
Число 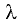
соответствующим вектору 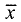
Перенеся правую часть (2.15) в левую и принимая во внимание
соотношение 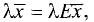
Уравнение (2.16) эквивалентно системе линейных однородных
уравнений
Для существования ненулевого решения системы линейных
однородных уравнений (2.17) необходимо и достаточно, чтобы
определитель коэффициентов этой системы равнялся нулю, т.е.
Этот определитель является многочленом n-й степени относительно
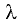
уравнение (2.18) — характеристическим уравнением матрицы А. Корни характеристического уравнения соответствуют собственным числам матрицы А. Определив набор этих чисел, для каждого из них можно найти собственный вектор.
Пример:
Найти собственные числа и собственные векторы
матрицы
Решение:
Характеристическое уравнение этой матрицы имеет вид
Корни характеристического уравнения
Для двух переменных система уравнений (2.17), эквивалентная
уравнению (2.15) собственного вектора, представляется в виде
Подставив сюда значения корней 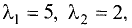
системы уравнений:
Каждая система является одним уравнением, что и следовало
ожидать. Это связано с тем, что определитель системы равен нулю.
Из первой системы для 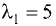
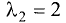
координаты собственных векторов связаны соотношениями
Поскольку 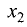
значению матрицы соответствует бесконечное множество собственных векторов различной длины. Положим 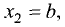
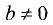
Решение заданий и задач по предметам:
Дополнительные лекции по высшей математике:




















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
🔍 Видео
Решение систем уравнений второго порядка. 8 класс.Скачать

Решение системы уравнений методом ГауссаСкачать

Решение систем линейных алгебраических уравнений методом Крамера.Скачать
§30 Системы линейных алгебраических уравненийСкачать

МЕТОД АЛГЕБРАИЧЕСКОГО СЛОЖЕНИЯ 😉 СИСТЕМЫ УРАВНЕНИЙ ЧАСТЬ II #математика #егэ #shorts #профильныйегэСкачать

Система с тремя переменнымиСкачать

Решение систем уравнений методом подстановкиСкачать

ФСР. Система однородных уравнений. Общее решениеСкачать

Урок 93. Системы и совокупности линейных неравенств с одной переменной (8 класс)Скачать

Решение систем уравнений методом сложенияСкачать

Алгебра 9. Урок 9 - Системы неравенствСкачать