Системы двух уравнений первой степени с двумя неизвестными 7 класс никольский

Презентация к уроку по теме «Системы двух уравнений первой степени с двумя неизвестными» в 7 классе

Просмотр содержимого документа
«Методическая разработка к уроку по теме: «Системы двух уравнений первой степени с двумя неизвестными»»

23.04.2020 Классная работа Системы двух уравнений первой степени с двумя неизвестными

Проверяем домашнее задание:

выполнить устно № 667* письменно № 674(г-е), 675(г), 676(д, е), 677(ж, з), 678(ж, з)

Ученик задумал два числа и сказал, что сумма этих чисел равна 12, а их разность равна 2. Какие числа задумал ученик?

Систему уравнений принято записывать с помощью фигурной скобки. Составленную систему уравнений можно записать так:

Обозначим первое число буквой х , а второе буквой у . По условию задачи сумма чисел равна 12, т.е.

Пара значений переменных х=7, у=5 служит решением каждого уравнения системы, так как оба равенства 7+5=12 и 7-5=2 являются верными.

Такую пару называют решением системы уравнений .

Мы составили два уравнения с двумя неизвестными. Чтобы ответить на вопрос задачи, надо найти такие значения неизвестных, которые обращают в верное числовое равенство каждое из уравнений х+у=12 и х-у=2 , т.е. найти общие решения этих уравнений.

В таких случаях говорят, что требуется решить систему уравнений.

Так как разность чисел равна 2, то

Что называется системой двух уравнений с двумя неизвестными?

Что называется решением системы двух уравнений с двумя неизвестными?

Решением системы двух уравнений с двумя неизвестными называется пара значений переменных, обращающая каждое уравнение системы в верное числовое равенство.

Что значит «решить систему уравнений»?

Решить систему уравнений – значит найти все её решения или установить, что решений нет .

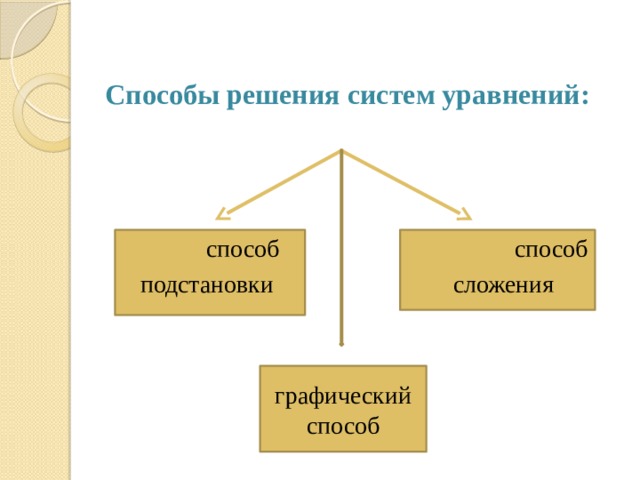
Способы решения систем уравнений:

• На уроке мне понравилось…
• На уроке мне не понравилось…
• Я узнал о…
• Я научился…

Ответьте на вопросы:

• Что такое система уравнений?
• Какие существуют способы решения систем уравнений?

Домашнее задание Изучить п.10.2; выполнить устно № 685, 686; письменно 689(г), 692(в, г), 693(б)

Видео:7 класс. Уравнения первой степени с двумя неизвестными.Скачать

Алгебра. 7 класс

Конспект урока

Системы двух уравнений первой степени с двумя неизвестными

Перечень рассматриваемых вопросов:

• Линейные уравнения.
• Корень уравнения;
• Решение линейных уравнений.

Уравнение – это равенство, включающее в себя переменную, значение которой нужно вычислить.

Корень уравнения – это число, при подстановке которого в уравнение получается верное равенство.

Переменная – символ, используемый для представления величины, которая может принимать любое из ряда значений.

Свободный член – член уравнения, не содержащий неизвестного.

Решить уравнение – значит найти все его корни или установить, что их нет.

Преобразование – это действия, выполняемые с целью замены исходного выражения на выражение, которое будет тождественно равным исходному.

Решить систему это значит найти все её решения.

Преобразование – это действия, выполняемые с целью замены исходного выражения на выражение, которое будет тождественно равным исходному.

Решение данной системы всякая пара значений неизвестных, удовлетворяющая обоим уравнениям, образующим систему.

Если отыскиваются общие решения двух или нескольких уравнений, то говорят, что эти уравнения образуют систему.

1. Никольский С. М. Алгебра: 7 класс. // Никольский С. М., Потапов М. К., Решетников Н. Н., Шевкин А. В. – М.: Просвещение, 2017. – 287 с.

1. Чулков П. В. Алгебра: тематические тесты 7 класс. // Чулков П. В. – М.: Просвещение, 2014 – 95 с.
2. Потапов М. К. Алгебра: дидактические материалы 7 класс. // Потапов М. К., Шевкин А. В. – М.: Просвещение, 2017. – 96 с.
3. Потапов М. К. Рабочая тетрадь по алгебре 7 класс: к учебнику С. М. Никольского и др. «Алгебра: 7 класс». 1, 2 ч. // Потапов М. К., Шевкин А. В. – М.: Просвещение, 2017. – 160 с.

Теоретический материал для самостоятельного изучения.

Пусть даны 2 уравнения с двумя неизвестными, например: x + 2y = 15 и x + 2y = 7.

Каждое из них имеет бесконечное множество решений. Поставим вопрос: среди всех этих решений не будут ли общие для обоих уравнений?

Такие общие решения могут быть, а могут и не быть. Так, общим решением данных уравнений будет то, что легко проверить подстановкой. (Дальше будет показано, что других общих решений эти уравнения иметь не могут).

Но, уравнения не имеют ни одного общего решения. В самом деле, какие бы значения мы ни подставляли, при любых x и y выражение x + 2y не может одновременно равняться 15 и 7. Поэтому ни одно решение первого уравнения не может быть решением второго и ни одно решение второго уравнения не может быть решением первого.

Если отыскиваются общие решения двух или нескольких уравнений, то говорят, что эти уравнения образуют систему.

Всякая пара значений неизвестных, удовлетворяющая обоим уравнениям, образующим систему, называется решением данной системы.

Решить систему это значит найти все её решения.

Решать системы двух уравнений можно с помощью:

• способа подстановки;
• способа уравнивания коэффициентов.

Способ подстановки состоит в том, что:

1) из одного уравнения мы находим выражение одного из неизвестных, например x, через известные величины и другое неизвестное у;

2) найденное выражение подставляем во второе уравнение, в котором после этой подстановки будет содержаться только одно неизвестное у;

3) решаем полученное уравнение и находим значение у;

4) подставляя найденное значение у в выражение неизвестного x, найденное в начале решения, получаем значение х.

Способ уравнивания коэффициентов:

1) обе части одного уравнения умножаются на некоторый множитель; обе части второго уравнения умножаются на другой множитель. Эти множители подбираются так, чтобы коэффициенты при одном из неизвестных в обоих уравнениях после их умножения на эти множители имели одну, и ту же абсолютную величину;

2) складываем два уравнения или вычитаем их друг из друга, смотря по тому, имеют ли уравненные коэффициенты различные или одинаковые знаки; этим одно из неизвестных исключается;

3) решаем полученное уравнение с одним неизвестным;

4) другое неизвестное можно найти тем же приемом, но обычно, проще всего, подставить найденное значение первого неизвестного в любое из данных уравнений и решить получившееся уравнение с одним неизвестным.

В элементарной математике рассматривают только некоторые простые частные случаи систем уравнений второй или высшей степени. Такова в частности, система

Разбор заданий тренировочного модуля

Решим систему, используя метод уравнивания коэффициентов. В данной системе коэффициенты уже уравнены, потому просто сложим почленно оба уравнения, получаем:

Задание 2. Какие значения переменных удовлетворяют системе уравнений:

Решим данную систему, используя метод уравнивания коэффициентов. В данной системе коэффициенты уже уравнены, потому просто вычтем почленно из первого уравнения второе, получаем:

Видео:Алгебра 7 класс (Урок№46 - Системы двух уравнений первой степени с двумя неизвестными.)Скачать

Презентация «Линейные уравнения первой степени с двумя неизвестными» 7 класс (Учебник С.М. Никольского и др.)

Код для использования на сайте:

Скопируйте этот код и вставьте себе на сайт

Для скачивания поделитесь материалом в соцсетях

После того как вы поделитесь материалом внизу появится ссылка для скачивания.

Подписи к слайдам:

§10. Системы линейных уравнений

Мурастова А.В., учитель математики

МБОУ СОШ №3 г. Ноябрьск

Алгебра. 7 класс.

Учебник С.М.Никольского и др.

В нашем учебнике уравнение записано в таком виде:

a, b, c – данные числа;

хотя бы одно из чисел а и b не равно 0;

а и b – коэффициенты при неизвестных;

с – свободный член;

х и у – неизвестные (переменные).

Перепишите уравнение в заданном виде

• Перепишите уравнение в заданном виде
• Назовите а, b и с

Разбор типичных заданий

Возьмём пару чисел (х0 ; у0)

Подставим их в уравнение:

2 · 1 – 1 · (-1) – 3 = 2+1-3 =0

Тогда 2·(- 2) –у – 3 = 0

или – 4 – у – 3 = 0 – получилось линейное уравнение с одной переменной. Решив его, найдем у.

Видео:Алгебра 7 класс (Урок№45 - Уравнения первой степени с двумя неизвестными.)Скачать

Урок алгебры в 7 классе на тему «Системы двух уравнений первой степени с двумя неизвестными»

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Рабочие листы и материалы для учителей и воспитателей

Более 2 500 дидактических материалов для школьного и домашнего обучения

Столичный центр образовательных технологий г. Москва

Получите квалификацию учитель математики за 2 месяца

от 3 170 руб. 1900 руб.

Количество часов 300 ч. / 600 ч.

Успеть записаться со скидкой

Форма обучения дистанционная

Видеолекции для
профессионалов

• Свидетельства для портфолио
• Вечный доступ за 120 рублей
• 311 видеолекции для каждого

6. Тема и номер урока в теме

Сахокия Дильбар Абдумавлоновна

МОУ Гимназия №1 г. Ярославля

Системы двух уравнений первой степени с двумя неизвестными

Алгебра. 7 класс: учебник для общеобразоват. организаций/ ( С.М. Никольский, М.К.Потапов, Н.Н.Решетников, А.В.Шевкин).- 3-е изд. -М.: Просвещение, 2016.- 287 с.: ил. – (МГУ – школе).

приобретение новых знаний с использованием ранее изученного материала при решении систем двух уравнений первой степени с двумя неизвестными , выработка умений и навыков в решении систем уравнений методом подстановки, их применение к решению систем двух уравнений первой степени с двумя неизвестными и решению задач.

9. Планируемые результаты:

предметные: уметь в процессе реальной ситуации использовать навыки решения систем двух уравнений первой степени с двумя неизвестными

личностные: умение работать в парах, слушать собеседника и вести диалог, аргументировать свою точку зрения

метапредметные: уметь обрабатывать информацию; формировать коммуникативную компетенцию учащихся; выбирать способы решения задач в зависимости от конкретных условий; контролировать и оценивать процесс и результаты своей деятельности

10. Задачи урока:

образовательные (формирование познавательных УУД): обеспечить осознанное усвоение способа подстановки при решении систем двух уравнений первой степени с двумя неизвестными; закрепить навыки и умения применять алгоритмы при решении систем двух уравнений первой степени с двумя неизвестными, создание условий для систематизации, обобщения и углубления знаний учащихся при решении систем двух уравнений первой степени с двумя неизвестными.

воспитательные (формирование коммуникативных и личностных УУД): формировать умение слушать и вступать в диалог, внимательность и аккуратность в вычислениях; воспитывать чувство взаимопомощи, уважительное отношение к чужому мнению, культуру учебного труда, требовательное отношение к себе и своей работе.

развивающие (формирование регулятивных УУД): способствовать развитию творческой активности учащихся; повысить познавательный интерес к предмету; развитие навыков и способностей критического мышления (навыков сопоставления, формулирования и проверки гипотез — правил решения систем уравнений, умений анализировать способы решения систем уравнений); развитие не только логического, но и образного мышления, фантазии детей и их способности рассуждать.

11. Тип урока: Урок открытия нового знания.

12. Формы работы учащихся: фронтальная, работа в парах, индивидуальная

13. Необходимое оборудование: доска, экран, проектор, компьютер, документ камера, карточки самооценки.

14. Структура и ход урока

Коммуникативные: планирование учебного сотрудничества с учителем и сверстниками.

Регулятивные: организация своей учебной деятельности

Личностные: мотивация учения, уважение личности и её достоинства, доброжелательное отношение к окружающим

2. Постановка цели и задач урока. Мотивация учебной деятельности учащихся.

Обеспечение мотивации учения детьми, принятие ими целей урока.

Мотивирует учащихся, вместе с ними определяет цель урока через решение систем двух уравнений первой степени с двумя неизвестными подбором, с выходом к решению систем двух уравнений первой степени с двумя неизвестными методом подстановки, акцентирует внимание учащихся на значимость темы

Работают устно, повторяют пройденный ранее материал. Формулируют тему урока. Записывают дату в тетрадь, тему и цель урока.

Познавательные: умение осознанно и произвольно строить речевое высказывание в устной форме, умение самостоятельно формулировать цели.

Регулятивные: целеполагание, планирование

Коммуникативные: умение вступать в диалог, участвовать в коллективном обсуждении вопроса.

3. Применение знаний и умений в новой ситуации

Показать разнообразие систем двух уравнений первой степени с двумя неизвестными

Организация и контроль за процессом решения систем двух уравнений первой степени с двумя неизвестными методом подстановки

Решают систему двух уравнений совместно с учителем. Формулируют алгоритм решения систем двух уравнений первой степени с двумя неизвестными методом подстановки. Работают в парах над поставленными задачами. Защита и представление решения.

Познавательные: формирование интереса к данной теме.

Личностные: формирование готовности к самообразованию.

Коммуникативные: умение высказывать свою точку зрения, с уважением относиться к мнению других;

умение договариваться, находить общее решение практической задачи;

умение оформлять свои мысли в устной и письменной форме;

Регулятивные: планирование своей деятельности для решения поставленной задачи и контроль полученного результата.

4.Выполнение упражнений, закрепление навыков

Работа у доски и на местах

Познавательные: умение осознанно и произвольно строить речевое высказывание в устной форме.

Регулятивные: планирование своей деятельности для решения поставленной задачи и контроль полученного результата.

5. Контроль усвоения, обсуждение допущенных ошибок и их коррекция.

Дать качественную оценку работы класса и отдельных обучаемых.

Выявляет качество и уровень усвоения знаний, а также устанавливает причины выявленных ошибок.

Учащиеся анализируют свою работу, выражают вслух свои затруднения и обсуждают правильность решения систем двух уравнений первой степени с двумя неизвестными методом подстановки

Личностные: формирование позитивной самооценки

Коммуникативные: умение с достаточной полнотой и точностью выражать свои мысли в соответствии с задачами и условиями коммуникации;

Регулятивные: умение выделить и осознать то, что уже усвоено и что еще подлежит усвоению, осознание качества и уровня усвоения;

6. Информация о домашнем задании

Обеспечение понимания детьми содержания и способов выполнения домашнего задания

Дает комментарий к домашнему заданию

Учащиеся записывают в дневники задание.

7 . Рефлексия (подведение итогов урока)

Дать количественную оценку работы учащихся

Подводит итоги работы групп и класса в целом.

Учащиеся сдают карточки самооценки.

Регулятивные: оценивание собственной деятельности на уроке

1. Организационный этап

Учитель приветствует учащихся, проверяет их готовность к уроку.

У каждого из вас на столах лежат карточки самооценки. Подпишите их. В течение урока мы с вами будем выполнять различные задания. По окончанию решения каждой задачи, вы должны оценить свою работу

Учащиеся слушают учителя, оформляют карточки.

2. Постановка цели и задач урока. Мотивация учебной деятельности учащихся.

1.Что нового мы узнали на предыдущих уроках? Приведите примеры уравнений первой степени с двумя неизвестными. Назовите коэффициенты при неизвестных и свободный член. Что называют решением уравнения первой степени с двумя неизвестными?

2. Составьте уравнение первой степени с двумя неизвестными по данным

_{3. Покажите, что пара чисел является решением уравнения}

_{4. Назовите коэффициенты при неизвестных и свободные члены уравнений системы:}

_{5. Какая пара чисел , является решением системы:}

6. Каким способом мы решили задачу из предыдущего пункта о возрасте брата и сестры? (Слайд №2)

Возможно ли таким способом, решить например такую систему уравнений? Удобен ли этот способ? Чему вы хотели бы научиться на этом уроке?

Итак, тема нашего урока: (Слайд №3)

Решение систем двух уравнений первой степени с двумя неизвестными методом подстановки

Наша цель на уроке?

Научится решать системы двух уравнений первой степени с двумя неизвестными, составить алгоритм решения системы двух уравнений первой степени с двумя неизвестными, научиться использовать его при решении упражнений

Итак, приступаем к решению системы двух уравнений первой степени с двумя неизвестными.

Решить в классе:

_{Пример 2.} Метод решения остаётся тем же.

Выведем алгоритм решения системы двух уравнений первой степени с двумя неизвестными способом подстановки

Алгоритм решения системы двух уравнений первой степени с двумя неизвестными методом подстановки

Одно из неизвестных ( например у ), выразить через другое ( выбираем удобную неизвестную, с коэффициентом 1 или 2 ) неизвестное из любого уравнения системы

Подставляем полученное выражение вместо у , в другое уравнение системы

Решаем полученное уравнение с одним неизвестным х

Подставив найденное значение в формулу, для у , найдем

Пара чисел и будет единственным решением системы.

(Слайд №4) выдать каждому ученику

1.Уравнение первой степени с двумя неизвестными и системы двух уравнений первой степени с двумя неизвестными. Приводят примеры, называют коэффициенты

Решением уравнения называют пару чисел _{, которая обращает уравнение в верное равенств}

2,3,4,5,6 учащиеся предлагают свои решения. По окончании работы над каждым примером, оценивают результат своей деятельности на листах самооценки.

Отвечают на поставленные вопросы

Предполагаемый ответ: методом подбора.

Нет, не очень удобен.

Решать системы двух уравнений первой степени с двумя неизвестными

Формулируют тему и цель урока, записывают в тетради дату и тему урока.

Предполагаемый ответ: н аучится решать системы двух уравнений первой степени с двумя неизвестными, составить алгоритм решения системы двух уравнений первой степени с двумя неизвестными методом подстановки, научиться использовать его при решении упражнений

Учащиеся решают систему,

записывают решение задачи в тетрадь.

По окончании работы над каждой системой, оценивают результат своей деятельности на листах самооценки.

Выводят алгоритм решения системы двух уравнений первой степени с двумя неизвестными

3. Применение знаний и умений в новой ситуации

Ну а теперь — работа в парах.

Решают системы уравнений на выбор самостоятельно в парах (слайд №5)

Решаем из учебника: №698 (б, г,е )

Учащиеся в группах выполняют решение выбранных задач.

Ребятам предлагается работа в парах, предлагаются на выбор несколько систем

В классе 12 пар. Задачу необходимо решить, оформить решение и «защитить» свое решение (используется документ камера)

По окончании работы над каждым примером, оценивают результат своей деятельности на листах самооценки.

У доски отвечает один ученик, остальные оформляют решение задачи в тетради

оценивают результат своей деятельности на листах самооценки.

4 . Контроль усвоения, обсуждение допущенных ошибок и их коррекция

Наш урок подходит к концу. Давайте обсудим: какие задачи вызвали у вас затруднения и почему?

Учащиеся анализируют свою работу, выражают вслух свои затруднения и обсуждают правильность решения задач.

5. Информация о домашнем задании

Домашнее задание: (Слайд №6)

на выбор и по желанию один пример из №699

2. Придумать и решить задачу, при решении которой надо будет применить систему двух уравнений

Учащиеся получают домашнее задание, записывают в дневник, выбирают задание.

6. Рефлексия (подведение итогов урока)

1. Понятен ли способ подстановки при решении систем двух уравнений первой степени с двумя неизвестными?

2. Что вызвало затруднения?

3. Что сегодня на уроке было интересно?

4. Где можно встретиться с необходимостью решать такие системы?

Собираются карточки самооценки и выставляются оценки за работу на уроке.

🎬 Видео

Алгебра 7 класс (Урок№48 - Решение систем двух линейных уравнений с двумя неизвестными.)Скачать

7 класс, 37 урок, Системы двух линейных уравнения с двумя переменными. Основные понятияСкачать

Системы двух уравнений первой степени с двумя неизвестнымиСкачать

Урок по теме СПОСОБ ПОДСТАНОВКИ 7 классСкачать

Решение систем уравнений методом подстановкиСкачать

Уравнения первой степени с двумя неизвестнымиСкачать

Алгебра.7 класс (Урок№42 - Уравнения первой степени с одним неизвестным.)Скачать

Урок СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ С ДВУМЯ ПЕРЕМЕННЫМИ 7 КЛАСССкачать

Линейное уравнение с двумя переменными. 7 класс.Скачать

7 класс. Система уравнений первой степени с 2 неизвестнымиСкачать

Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

Графический способ исследования систем двух уравнений первой степени с двумя неизвестнымиСкачать

Решение систем уравнений. Методом подстановки. Выразить YСкачать

7 класс, 40 урок, Системы двух линейных уравнений с двумя переменными как математические моделиСкачать

Графический способ решения систем двух уравнений первой степени с двумя неизвестнымиСкачать

Системы двух уравнений первой степени с двумя неизвестнымиСкачать

Уравнения первой степени с двумя неизвестными, 7 класс, 190423Скачать