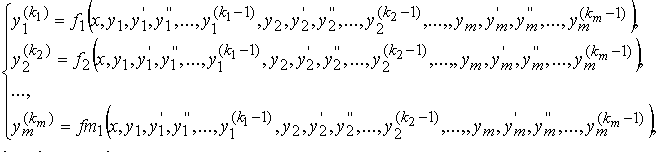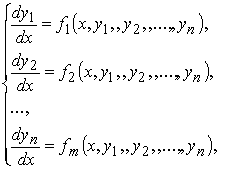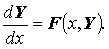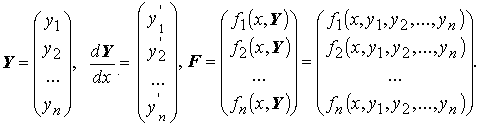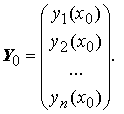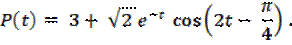Системы дифференциальных уравнений векторная запись

СИСТЕМЫ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ. ОСНОВНЫЕ ПОНЯТИЯ

Высшая математика

Система обыкновенных дифференциальных уравнений n –го порядка

может быть записана в канонической форме :

в нормальной форме

или в векторной форме

При описании систем дифференциальных уравнений удобнее пользоваться векторной формой записи.

Решением системы обыкновенных дифференциальных уравнений Y ‘ = F ( x , Y ) называется вектор–функция Y ( x ) = Φ ( x ) , которая определена и непрерывно дифференцируема на промежутке ( a ; b ) и удовлетворяет системе Y ‘ = F ( x , Y ) на этом промежутке.

Задачей Коши для системы обыкновенных дифференциальных уравнений называется следующая задача: найти решение Y ( x ) системы Y ‘ = F ( x , Y ) такое, что Y ( x ₀) = Y ₀ . Здесь

Частным решением системы дифференциальных уравнений называется решение какой–нибудь ее задачи Коши.

Вектор–функция Y = Y ( x , C ) = Y ( x , C ₁, C ₂, … , C _n) , зависящая от n произвольных постоянных C ₁, C ₂, … , C _n называется общим решением системы дифференциальных уравнений на [ a ; b ] , если:

— при любых допустимых значениях постоянных C ₁, C ₂, … , C _n функция Y ( x , C ) является решением системы на [ a ; b ] ;

— какова бы ни была начальная точка ( x ₀, Y ₀) из области определения правой части системы, существуют такие значения C *₁, C *₂, … , C *_n постоянных C ₁, C ₂, … , C _n , что функция

Y ( x , C *₁, C *₂, … , C *_n ) является решением задачи Коши Y ( x ₀) = Y ₀ .

Пусть Y ( x ) = Φ ( x ) — решение системы, определенное на [ a , b ] . Тогда множество точек , x ∈ [ a , b ] — кривая в пространстве R _n .

Эту кривую называют фазовой траекторией или просто траекторией системы, а пространство R _n , в котором расположены фазовые траектории, фазовым пространством системы .

Пусть Y ( x ) = Φ ( x ) — решение системы Y ‘ = F ( x , Y ) , определенное на [ a , b ] .

Интегральная кривая системы определяется уравнением Y = Φ ( x ) и изображается в ( n + 1)–мерном пространстве R _n+1

Фазовая траектория — проекция интегральной кривой на пространство R _n.

Нормальная система дифференциальных уравнений. Векторная запись нормальной системы.

Общий вид дифференциального уравнения первого порядка есть F(x,y,y¢)=0. Если это уравнение можно разрешить относительно у¢, т.е. записать в виде у¢=f(x,y), то говорят, что уравнение записано в нормальной форме (или в форме Коши).

Рассмотрим геометрическую трактовку нахождения решений уравнения. Возьмём некоторую точку (x₀,y₀) из области определения D функции f(x,y). Пусть у=j(х) – интегральная кривая, проходящая через эту точку. Из уравнения вытекает, что j¢(х₀)=(х₀,у₀). Таким образом, угловой коэффициент касательной к интегральной кривой, проходящей через точку (х₀,у₀) равен (прих=х₀) числу f(х_0,у₀).

Построим теперь для каждой точки (х₀,у₀) из области определения прямую, проходящую через эту точку и имеющую угловой коэффициент, равный f(х₀,у₀). В этом случае принято говорить, что эта прямая определяет направление в точке (х₀,у₀), а на множестве D задано поле направлений.

Если каждое уравнение, входящее в систему, является дифференциальным, т.е. имеет вид соотношения, связывающего неизвестные функции и их производные, то говорят о системе дифференциальных уравнений. Так система дифференциальных уравнений первого порядка с двумя неизвестными функциями записывается обычно в виде

На системы дифференциальных уравнений естественным образом обощается постановка задачи Коши для одного уравнения. Например, в случае данной системы задача Коши состоит в нахождении решения х₁(t),x₂(t), удовлетворяющих начальным условиям х₁(t₀)= х₁ 0 , x₂(t₀)= x₂ 0 , где t_0, х₁ 0 , x₂ 0 – заданные числа. Для случая системы может быть доказана теорема существования и единственности решения задачи Коши, аналогичная теореме для одного уравнения.

Теорема существования и единственности решения задачи Коши.

Если в некоторой окрестности точки (х₀,у₀) функция f(х,у) определена, непрерывна и имеет непрерывную частную производную f¢_y, то существует такая окрестность точки (х₀,у₀), в которой задача Коши имеет решение, притом единственное. (приводится без доказательства)

Задача о нахождении решений дифференциального уравнения у¢=f(x,y), удовлетворяющих начальному условию у(х₀)=у₀ , называется задачей Коши.

К системам дифференциальных уравнений первого порядка в известном смысле сводятся уравнения (и системы уравнений) любого порядка. Пример.

Пусть дано уравнение у¢¢¢=f(x,y,y¢,y¢¢). Если обозначить функцию y¢и y¢¢ соответственно через m и n, то уравнение можно заменить системой

состоящей из трёх уравнений первого порядка с тремя неизвестными функциями.

Векторная запись нормальной системы. (со слов Гончаренко)

Пусть дана нормальная система из n уравнений с n неизвестными.

Представим набор решений как вектор х= (x₁,x₂,…,x_n) в проистранстве R n .

Функцию также можно записать в векторном виде f=(f(x),f(x),…,f(x)).

Векторная запись всей системы будет выглядеть следующия образом:

Системы дифференциальных уравнений векторная запись

Lv 1 = f, Lv 2 = f,

То есть сумма решений линейного однородного и линейного неоднородного уравнений (с тем же L) есть решение того же неоднородного уравнения; разность двух решений линейного неоднородного уравнения есть решение линейного однородного уравнения.

2.3. Линейная зависимость вектор-функций.

Вектор-функции x 1 (t), . x k (t) называются линейно зависимыми на интервале (или на множестве) М , если найдутся такие постоянные числа c₁. c_k, из которых хотя бы одно не равно нулю, что при всех t Î M имеем

Вектор-функции линейно независимы на M , если они не являются линейно зависимыми на M, то есть если равенство (12) (при всех t Î M одновременно) возможно лишь в случае c₁ = . = с_k = 0.

Понятие линейной зависимости вектор-функций на данном множестве M, содержащем более одной точки, отличается от известного из алгебры понятия линейной зависимости векторов.

Если вектор-функции x 1 (t), . x k (t) линейно зависимы на M, то при каждом t Î M их значения являются линейно зависимыми векторами, это следует из (12). Обратное неверно.

x 1 (t) = (1,1) и x 2 (t) = (t, t)

при любом t являются линейно зависимыми векторами.

Но как вектор-функции, они на любом интервале ( α, β) линейно независимы, так как при постоянных с₁ и c₂ равенство

на всем интервале ( α, β) возможно лишь при с₁ = с₂ = 0.

Действительно, c₁x 1 (t) + c₂ x 2 (t) = 0 эквивалентно выполнению равенства

2.3. Детерминант Вронского.

Детерминант Вронского W (t) или вронскиан для n-мерных вектор-функций

х 1 (t). , x n ( t ) — это детерминант n-го порядка, столбцы которого состоят из координат этих вектор-функций.

Если вектор-функции x 1 (t), . x n (t) линейно зависимы, то их вронскиан W(t) ≡ 0.

Если вронскиан W(t) ≠ 0 ( $ t ), то вектор-функции x 1 (t), . x n (t) линейно независимы.

Если вектор-функции x 1 (t), . x n (t) являются решениями системы х’ = A(t)x с непрерывной матрицей A ( t ), и их вронскиан равен нулю хотя бы при одном значении t , то эти вектор-функции линейно зависимы и их вронскиан W(t) ≡ 0.

Для вектор-функций, не являющихся решениями, утверждение леммы 3 неверно. В частности, для вектор-функций примера 2

x 1 (t) = (1,1) и x 2 (t) = (t, t)

имеем: W(t) ≡ 0, а они линейно независимы.

Далее рассматриваются решения линейной системы

Фундаментальной системой решений называется любая система n линейно независимых решений.

Покажем, что фундаментальные системы существуют. Возьмем t₀ Î ( α, β) и любые n линейно независимых векторов b 1 , …, b n Î R n

Пусть х 1 (t). ,x n (t) — решения системы х’ = A(t)x с начальными условиями x j (t 0 ) = b j , j = 1. ,n.

Эти решения линейно независимы, так как при t = t₀ их значения — линейно независимые векторы b 1 . b n , и равенство (12) возможно только при c₁ = . = c_n = 0.

Общим решением системы дифференциальных уравнений называют множество функций, содержащее все решения этой системы и только их (или формулу, представляющую это множество при всевозможных значениях произвольных постоянных).

Теорема 5 (об общем решении).

Пусть x l (t). x n (t) — какие-нибудь n линейно независимых решений системы

Общее решение системы есть

Теорема 5 означает, что множество решений системы х’ = A(t)x (х Î R n ) есть n-мерное линейное пространство.

Базисом в этом пространстве служит любая фундаментальная система решений. Равенство (13) есть представление любого элемента этого пространства в виде линейной комбинации элементов базиса.

Фундаментальной матрицей системы х’ = A(t)x называется матрица X(t), столбцы которой составляют фундаментальную систему решений.

Из леммы 3 следует, что det X(t) = W(t) ≠ 0.

С помощью фундаментальной матрицы X(t) общее решение (13) записывается в виде

где с — вектор-столбец с произвольными координатами c₁. с_n (так как X(t)c — линейная комбинация столбцов матрицы X(t), равная правой части (13) с коэффициентами с₁. с_n.

Найти линейно независимые решения и фундаментальную матрицу для системы

Из второго уравнения имеем у = с₁ (произвольная постоянная). Подставляя в первое уравнение, получаем х’ = с₁. Отсюда х = c₁t + c₂.

Общее решение есть х = c₁t + c₂,

Полагая с₁ = 1, с₂ = 0, находим частное решение х₁ = t,

y₁ = 1, а полагая с₁ = 0, с₂ = 1, находим другое решение х₂ = 1,

y₂ = 0. Их вронскиан W(t) = -1 ≠ 0. И в силу следствия леммы 2 эти решения линейно независимы. Поэтому фундаментальной является матрица

X T = x 1 x 2 y 1 y 2 .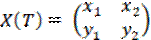

Теорема 6 (переход от одной фундаментальной матрицы к другой).

Пусть X(t) — фундаментальная матрица, С — неособая (det С ≠ 0) постоянная матрица n x n. Тогда Y(t) = X(t)C — фундаментальная матрица той же системы. По этой формуле из данной фундаментальной матрицы X(t) можно получить любую фундаментальную матрицу Y(t), подбирая матрицу С.

Теорема 7 . Общее решение линейной неоднородной системы (10)

есть сумма ее частного решения и общего решения линейной однородной системы

3. ПРИМЕНЕНИЕ ТЕОРИИ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ В ЗАДАЧАХ ЭКОНОМИКИ.

Дифференциальные уравнения занимают особое место в ма­тематике и имеют многочисленные приложения в большом спектре наук. Исследования природных процессов и изучение закономерностей общественных процессов приводят к построе­нию математических моделей, основой которых являются диф­ференциальные уравнения.

В дифференциальных уравнениях неизвестная функция со­держится вместе со своими производными. Основной задачей теории дифференциальных уравнений является изучение функ­ций, представляющих собой решения этих уравнений.

На этой лекции мы рассмотрим пример примене­ния теории дифференциальных уравнений в непрерывной мо­дели экономики, где независимой переменной является вре­мя t . Такие модели достаточно эффективны при исследовании эволюции экономических систем на длительных интервалах времени; они являются предметом исследования экономичес­кой динамики.

3.1. Модель рынка с прогнозируемыми ценами.

Рассмотрим модель рынка с прогнозируемыми ценами. В простых моделях рынка спрос и предложение обычно полагают зависящими только от текущей цены на товар. Однако спрос и предложение в реальных ситуациях зависят еще и от тен­денции ценообразования и темпов изменения цены. В моделях с непрерывными и дифференцируемыми по времени t функци­ями эти характеристики описываются соответственно первой и второй производными функции цены P ( t ).

Рассмотрим конкретный пример. Пусть функции спроса D и предложения S имеют следующие зависимости от цены Р и ее производных:

D(t) = 3P′′ – P′ – 2P +18,

S(t) = 4P′′ + P′ + 3P + 3. (14)

Принятые в (14) зависимости вполне реалистичны: поясним это на слагаемых с производными функции цены.

1. Спрос «подогревается» темпом изменения цены: если темп растет ( Р» > 0), то рынок увеличивает интерес к то­вару, и наоборот. Быстрый рост цены отпугивает покупателя, поэтому слагаемое с первой производной функции цены входит со знаком минус.

2. Предложение в еще большей мере усиливается темпом изменения цены, поэтому коэффициент при Р» в функции S ( t ) больше, чем в D ( t ) . Рост цены также увеличивает предложе­ние, потому слагаемое, содержащее Р’ , входит в выражение для S ( t ) со знаком плюс.

Требуется установить зависимость цены от времени. По­скольку равновесное состояние рынка характеризуется равен­ством D = S , приравняем правые части уравнений (14). После приведения подобных получаем

Соотношение (15) представляет линейное неоднородное дифференциальное уравнение второго порядка относительно функции P ( t ) . Как было установлено в предыдущем пункте, общее решение такого уравнения состоит из суммы какого-либо его частно­го решения и общего решения соответствующего однородного уравнения

Характеристическое уравнение имеет вид

Его корни — комплексно-сопряженные числа: k _1,2 = -1 ± 2 i, и, следовательно, общее решение уравнения (16) дается фор­мулой

где С₁ и С₂ — произвольные постоянные.

В качестве частно­го решения неоднородного уравнения (15) возьмем решение Р = P _st — постоянную величину как установившуюся цену. Подстановка в уравнение (15) дает значение P _st :

Таким образом, общее решение уравнения (15) имеет вид

Нетрудно видеть, что P ( t ) 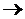P _st = 3 при t , т.е. все интегральные кривые имеют горизонтальную асимптоту Р = 3 и колеблются около нее. Это означает, что все цены стремятся к установившейся цене P _st с колебаниями около нее, причем амплитуда этих колебаний затухает со временем.

3.2. Частные решения: задача Коши и смешанная задача.

Приведем частные решения этой задачи в двух вариантах: задача Коши и смешанная задача.

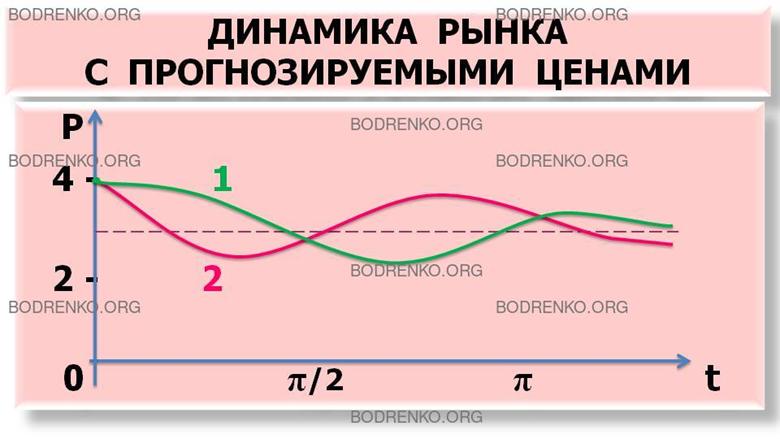
1. Задача Коши. Пусть в начальный момент времени из­вестна цена, а также тенденция ее изменения: При t =0

Подставляя первое условие в формулу общего решения (17), получаем

P(t) = 3 + e –t (cos 2t + C₂ sin 2t). (18)

Дифференцируя , имеем отсюда

Теперь реализуем второе условие задачи Коши:

Р’ (0) = 2 C₂ — 1 = 1, откуда C ₂ = 1 . Окончательно получаем, что решение задачи Коши имеет вид

P(t) = 3 + e –t (cos 2t + sin 2t).

или в более удобной форме:

P t = 3+ 2 e — t cos 2 t — π 4 .

2. Смешанная задача. Пусть в начальный момент времени известны цена и спрос:

Поскольку первое начальное условие такое же, как и в преды­дущем случае, то имеем и здесь решение (18). Тогда произ­водные функции Р( t ) выражаются формулами

Отсюда Р’(0) =2 C ₂ — 1 и Р»( 0 ) = —4 C ₂ — 3 . Подставляя эти равенства во второе условие задачи, т.е. D ( 0 ) = 16 , имеем с учетом вида D ( t ) из первой формулы (14): С₂ = -1. Итак, решение данной задачи имеет вид

или в более удобной форме:

P t = 3- 2 e — t sin 2 t — π 4 .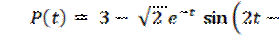

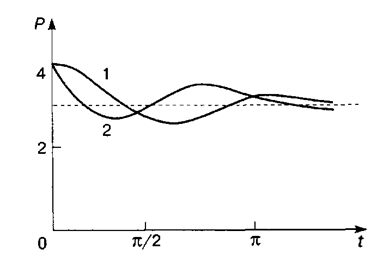
Интегральные кривые, соответствующие задачам 1 и 2, изоб­ражены на рисунке 1.

СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ

[1] Клюшин В. Л. Высшая математика для экономистов: Учебное пособие. — М.: ИНФРА-М, 2009. — 448 с. — (Учебники РУДН).

[2] Колемаев В. А. Экономико-математическое моделирование. Моделирование макроэкономических процессов и систем: Учебник. М.: ЮНИТИ-ДАНА, 2005. — 295 с.

[3] Красс М.С., Чупрынов Б.П. Основы математики и ее приложения в экономическом образовании: Учебник. — 2-е изд., испр. — М.: Дело, 2001. — 688 с.

[4] Красс М.С., Чупрынов Б.П. Математика для экономистов. СПб.: Питер, 2005. – 464, ил. (Серия «Учебное пособие»).

[5] Филиппов А. Ф. Введение в теорию дифференциальных уравнений: Учебник. Изд. 2-е, испр. М.: КомКнига, 2007. — 240 с.

🔍 Видео