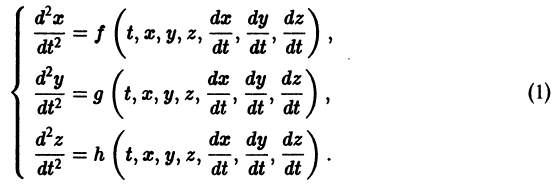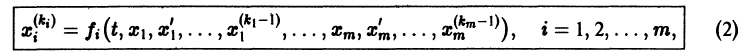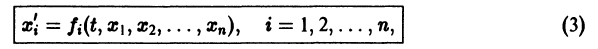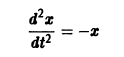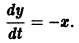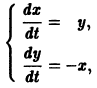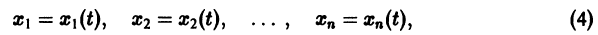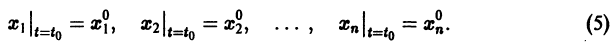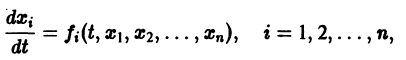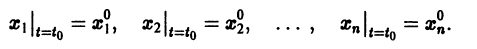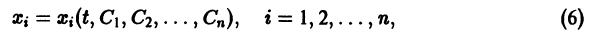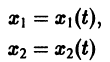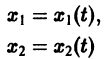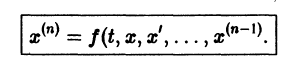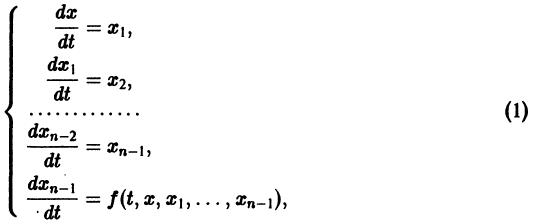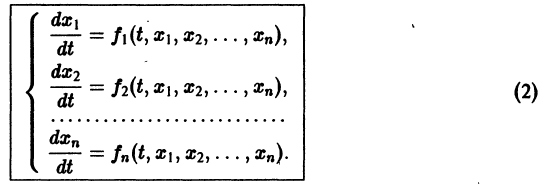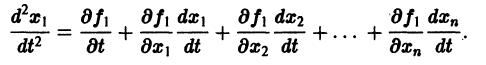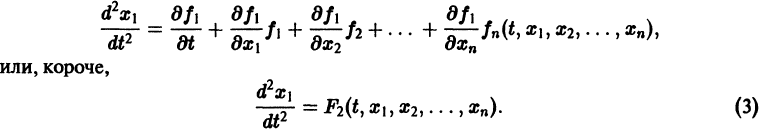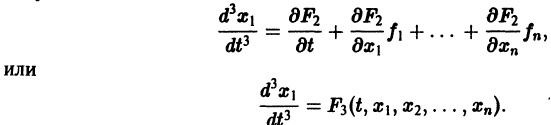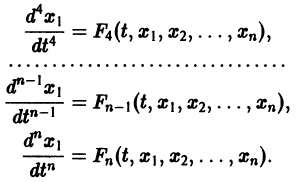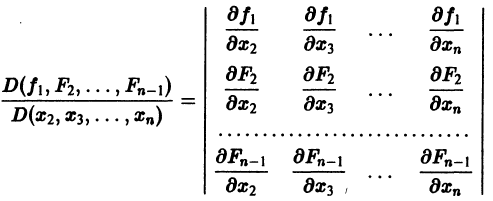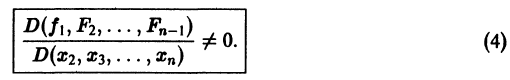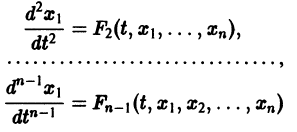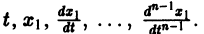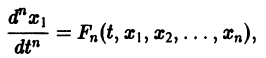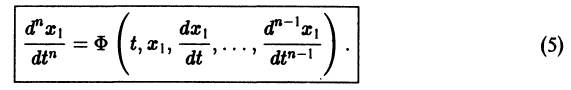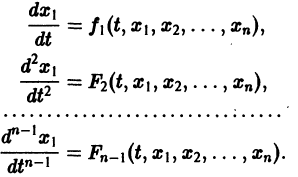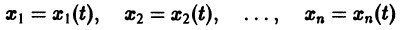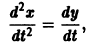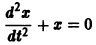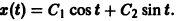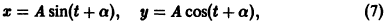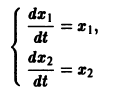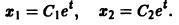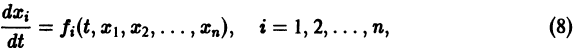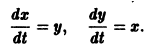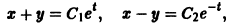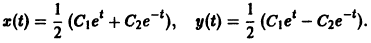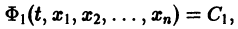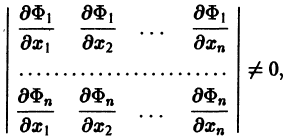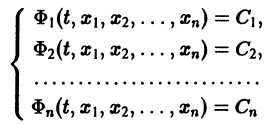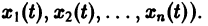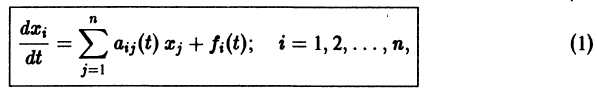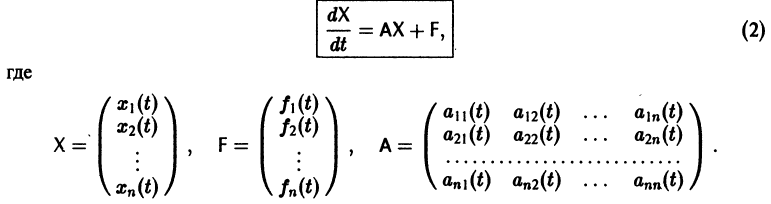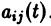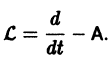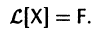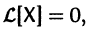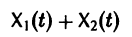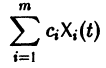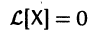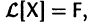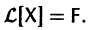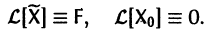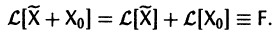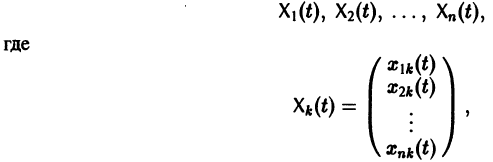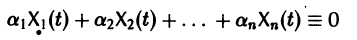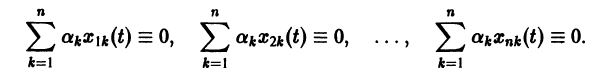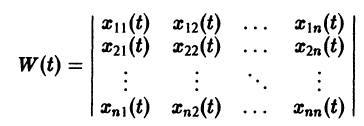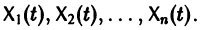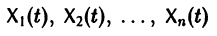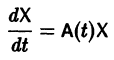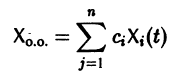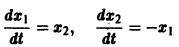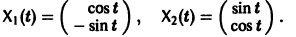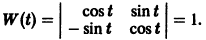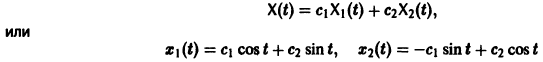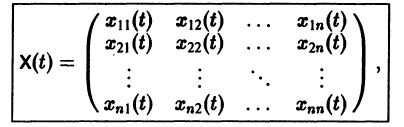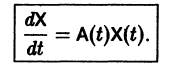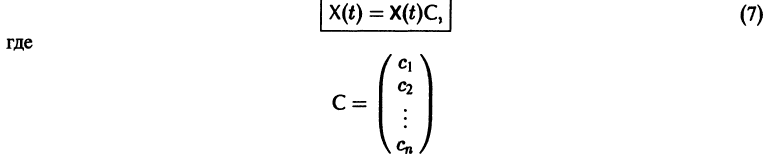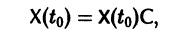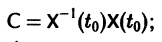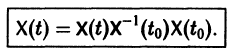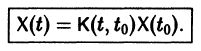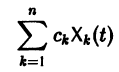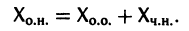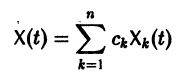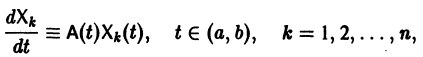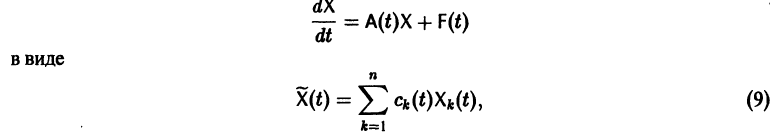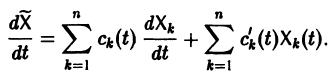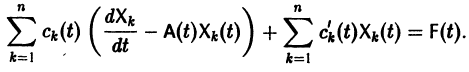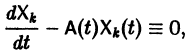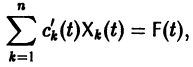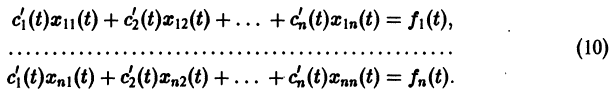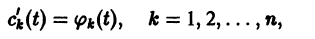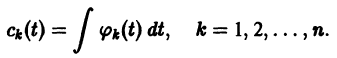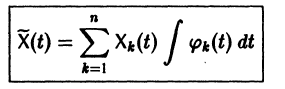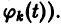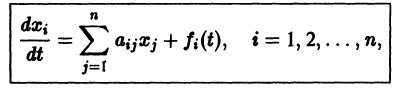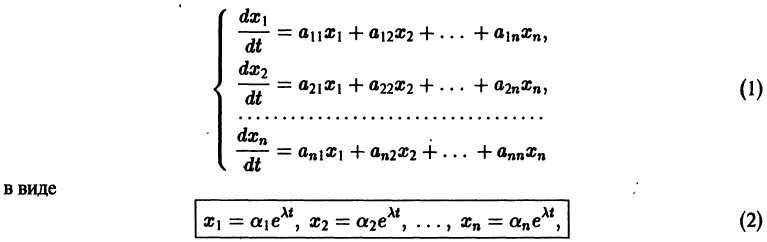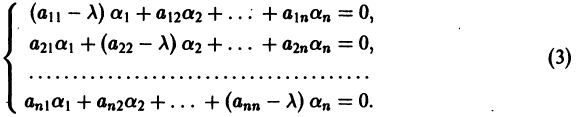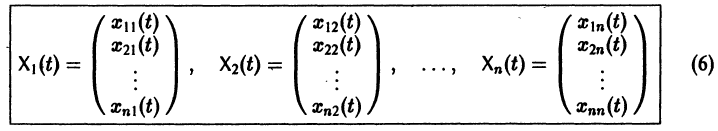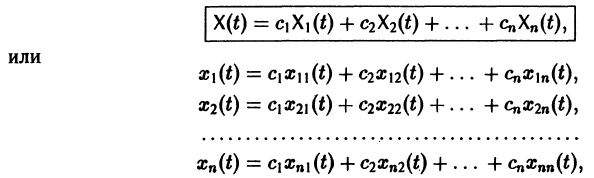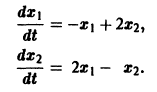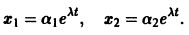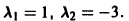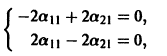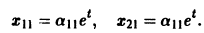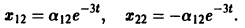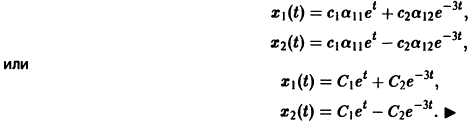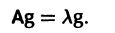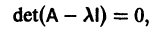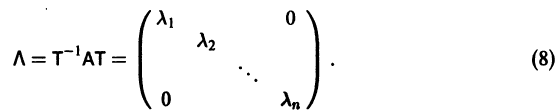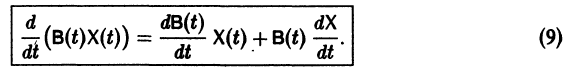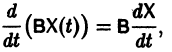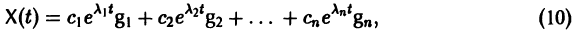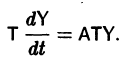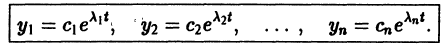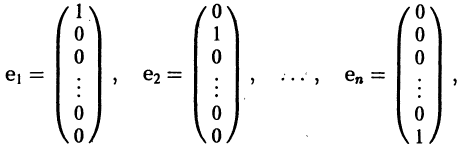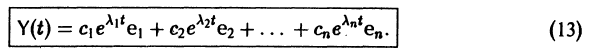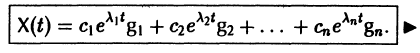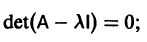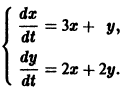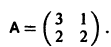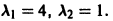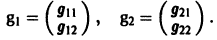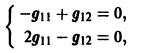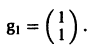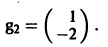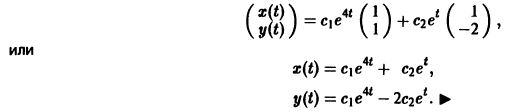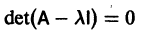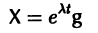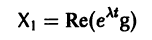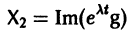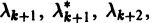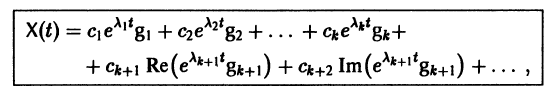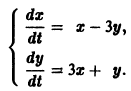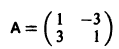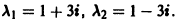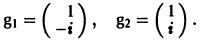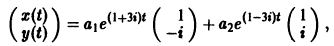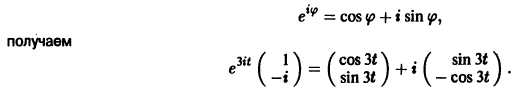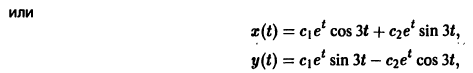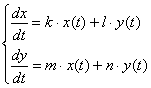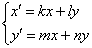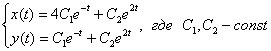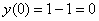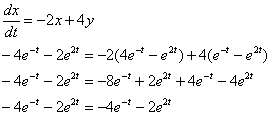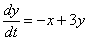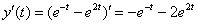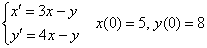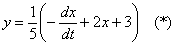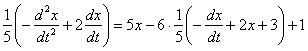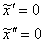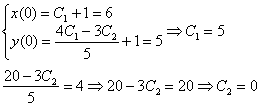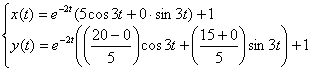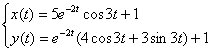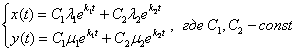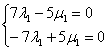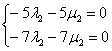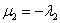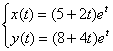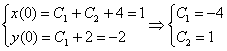Системы дифференциальных уравнений собственные векторы

Видео:Решение системы дифференциальных уравнений методом ЭйлераСкачать

СИСТЕМЫ ЛИНЕЙНЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ. СВЯЗЬ С УРАВНЕНИЯМИ n-ГО ПОРЯДКА. МЕТОД СОБСТВЕННЫХ ВЕКТОРОВ

Дадим основные определения, связанные с системами линейных дифференциальных уравнений.

1. Если система к дифференциальных уравнений, связывающая независимую переменную х и к функций уДх), . у_А(х), разрешена относительно старших производных этих функций yf A) (x), . у[ Рк х), т.е. имеет вид

то она называется канонической, причем число п = р₁ + р₂ +. + р_к называется порядком системы.

Каноническая система (17.33) при р_х = р₂ = . = p_k = 1, т.е. система дифференциальных уравнений 1-го порядка

называется нормальной системой порядка п.

• 2. Решением системы (17.34) на интервале а ^

Пример 17.35. Решить систему уравнений У У7 сведя

ее к одному уравнению второго порядка.

? Выразим у₂ из первого уравнения: у₂ = 4у _{, =} или = .Получаем

собственный вектор = f^l и соответствующее корню Х _{ке ь .}

Если же для кратного корня X кратности к имеется только т линейно независимых собственных векторов, и т 2t :

Приравнивая коэффициенты при одинаковых степенях /, получаем

Итак, общее решение исходной системы имеет вид

Описанный метод нахождения решения системы линейных однородных дифференциальных уравнений (17.41) носит название метод собственных векторов.

Пример 17.43. Найти частное решение системы дифференциальных уравнений

удовлетворяющее начальному условию х(0) = 0, у(0) = 1, z(0) = -2.

• -Х -1 1
• ? Характеристическое уравнение 1 1 — X -1=0 имеет
• 2 -1 -X

Видео:Собственные векторы и собственные значения матрицыСкачать

Системы дифференциальных уравнений с примерами решения и образцами выполнения

Также как и обыкновенные дифференциальные уравнения, системы дифференциальных уравнений применяются для описания многих процессов реальной действительности. В частности, к ним относятся различного рода физические и химические процессы, процессы нефте- и газодобычи, геологии, экономики и т.д. Действительно, если некоторые физические величины (перемещение тела, пластовое давление жидкости в фиксированной точке с тремя координатами, концентрация веществ, объемы продаж продуктов) оказываются меняющимися со временем под воздействием тех или иных факторов, то, как правило, закон их изменения по времени описывается именно системой дифференциальных уравнений, т.е. системой, связывающей исходные переменные как функции времени и производные этих функций. Независимой переменной в системе дифференциальных уравнений может выступать не только время, но и другие физические величины: координата, цена продукта и т.д.

Видео:Собственные значения и собственные векторы матрицы (4)Скачать

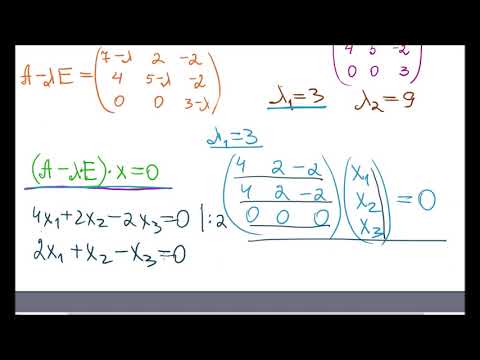
Решение систем дифференциальных уравнений

К системе дифференциальных уравнений приводит уже простейшая задача динамики точки: даны силы, действующие на материальную точку; найти закон движения, т. е. найти функции 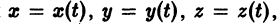выражающие зависимость координат движущейся точки от времени. Система, которая при этом получается, в общем случае имеет вид

Здесь x, у, z — координаты движущейся точки, t — время, f, g, h — известные функции своих аргументов.

Система вида (1) называется канонической. Обращаясь к общему случаю системы т дифференциальных уравнений с т неизвестными функциями 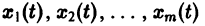аргумента t, назовем канонической систему вида

разрешенную относительно старших производных. Система уравнений первого порядка, разрешенных относительно производных от искомых функций,

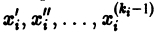
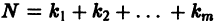
Если в (2) принять за новые вспомогательные функции, то общую каноническую систему (2) можно заменить эквивалентной ей нормальной системой, состоящей из уравнений. Поэтому достаточно рассматривать лишь нормальные системы.

Например, одно уравнение

является мастным случаем канонической системы. Положив 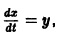в силу исходного уравнения будем иметь

В результате получаем нормальную систему уравнений

эквивалентную исходному уравнению.

Определение:

Решением нормальной системы (3) на интервале (а, Ь) изменения аргумента t называется всякая система n функций

дифференцируемых на интервале а

Теорема:

Существования и единственности решения задачи Коши. Пусть имеем нормальную систему дифференциальных уравнений

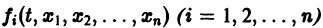
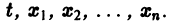
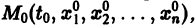
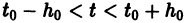
и пусть функции определены в некоторой (n + 1) — мерной области D изменения переменных Если существует окрестность точки в которой функции fi непрерывны по совокупности аргументов и имеют ограниченные частные производные по переменным то найдется интервал изменения t, на котором существует единственное решение нормальной системы (3), удовлетворяющее начальным условиям

Определение:

Система n функций

зависящих от t и n произвольных постоянных называется общим решением нормальной системы (3) в некоторой области существования и единственности решения задачи Коши, если

1) при любых допустимых значениях система функций (6) обращает уравнения (3) в тождества,

2) в области функции (6) решают любую задачу Коши.

Решения, получающиеся из общего при конкретных значениях постоянных называются частными решениями.

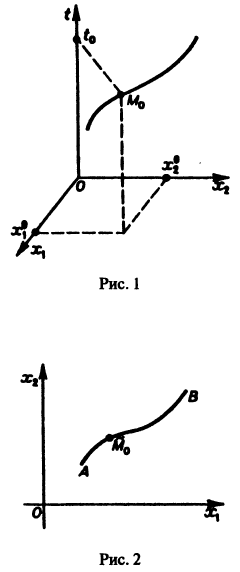
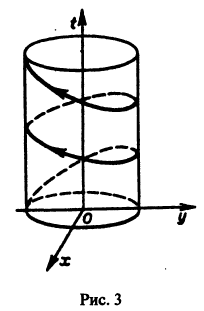
Обратимся для наглядности к нормальной системе двух уравнений,

Будем рассматривать систему значений t, x1, х2 как прямоугольные декартовы координаты точки трехмерного пространства, отнесенного к системе координат 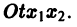Решение

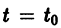
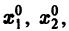
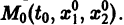
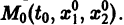
системы (7), принимающее при значения определяет в пространстве некоторую линию, проходящую через точку Эта линия называется интегральной кривой нормальной системы (7). Задача Коши для системы (7) получает следующую геометрическую формулировку: в пространстве переменных t, x1, х2 найти интегральную кривую, проходящую через данную точку (рис. 1). Теорема 1 устанавливает существование и единственность такой кривой.

Нормальной системе (7) и ее решению можно придать еще такое истолкование: будем независимую переменную t рассматривать как параметр, а решение

системы — как параметрические уравнения кривой на плоскости Эту плоскость переменных х1х2 называют фазовой плоскостью. В фазовой плоскости решение системы (7), принимающее при t = to начальные значения изображается кривой АВ, проходящей через точку (рис. 2). Эту кривую называют траекторией системы (фазовой траекторией). Траектория системы (7) есть проекция интегральной кривой на фазовую плоскость. По интегральной кривой фазовая траектория определяется однозначно, но не наоборот.

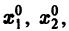
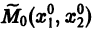
Методы интегрирования систем дифференциальных уравнений

Метод исключения

Один из методов интегрирования — метод исключения. Частным случаем канонической системы является одно уравнение n-го порядка, разрешенное относительно старшей производной

Введя новые функции 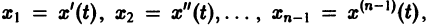заменим это уравнение следующей нормальной системой n уравнений:

т. е. одно уравнение n-го порядка эквивалентно нормальной системе (1)

Можно утверждать и обратное, что, вообще говоря, нормальная система п уравнений первого порядка эквивалентна одному уравнению порядка n. На этом и основан метод исключения для интегрирования систем дифференциальных уравнений.

Делается это так. Пусть имеем нормальную систему

Продифференцируем первое из уравнений (2) по t. Имеем

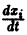
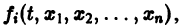
Заменяя в правой части производные их выражениями получим

Уравнение (3) снова дифференцируем по t. Принимая во внимание систему (2), получим

Продолжая этот процесс, найдем

Предположим, что определитель

(якобиан системы функций отличен от нуля при рассматриваемых значениях

Тогда система уравнений, составленная из первого уравнения системы (2) и уравнений

будет разрешима относительно неизвестных При этом выразятся через

Внося найденные выражения в уравнение

получим одно уравнение n-го порядка

Из самого способа его построения следует, что если 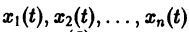есть решения системы (2), то функция х1(t) будет решением уравнения (5).

Обратно, пусть Х1(t) — решение уравнения (5). Дифференцируя это решение по t, вычислим 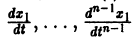и подставим найденные значения как известные функции

от t в систему уравнений

По предположению эту систему можно разрешить относительно т. е найти как функции от t.

Можно показать, что так построенная система функций

составляет решение системы дифференциальных уравнений (2). Пример:

Требуется проинтегрировать систему

Дифференцируя первое уравнение системы, имеем

откуда, используя второе уравнение, получаем

— линейное дифференциальное уравнение второго порядка с постоянными коэффициентами с одной неизвестной функцией. Его общее решение имеет вид

В силу первого уравнения системы находим функцию

Найденные функции x(t), y(t), как легко проверить, при любых значениях С1 и С2 удовлетворяют заданной системе.

Функции x(t), y(t) можно представить в виде

откуда видно, что интегральные кривые системы (6) — винтовые линии с шагом 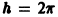и с общей осью х = у = 0, которая также является интегральной кривой (рис. 3).

Исключая в формулах (7) параметр t, получаем уравнение

так что фазовые траектории данной системы суть окружности с центром в начале координат — проекции винтовых линий на плоскость хОу.

При А = 0 фазовая траектория состоит из одной точки х = 0, у = 0, называемой точкой покоя системы.

Замечание:

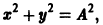
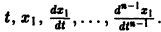
Может оказаться, что функции нельзя выразить через Тогда уравнения n-го порядка, эквивалентного исходной системе, мы не получим. Вот простой пример. Систему уравнений

нельзя заменить эквивалентным уравнением второго порядка относительно х1 или x2. Эта система составлена из пары уравнений 1-го порядка, каждое из которых интегрируется независимо, что дает

Метод интегрируемых комбинаций

Интегрирование нормальных систем дифференциальных уравнений

иногда осуществляется методом интегрируемых комбинаций.

Интегрируемой комбинацией называется дифференциальное уравнение, являющееся следствием уравнений (8), но уже легко интегрирующееся.

Пример:

Складывая почленно данные уравнения, находим одну интегрируемую комбинацию:

Вычитая почленно из первого уравнения системы второе, получаем вторую интегрируемую комбинацию:

Мы нашли два конечных уравнения

из которых легко определяется общее решение системы:

Одна интегрируемая комбинация дает возможность получить одно уравнение

связывающее независимую переменную t и неизвестные функции Такое конечное уравнение называется первым интегралом системы (8). Иначе: первым интегралом системы дифференциальных уравнений (8) называется дифференцируемая функция не равная тождественно постоянной, но сохраняющая постоянное значение на любой интегральной кривой этой системы.

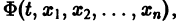
Если найдено п первых интегралов системы (8) и все они независимы, т. е. якобиан системы функций отличен от нуля:

то задача интефирования системы (8) решена (так как из системы

определяются все неизвестные функции

Системы линейных дифференциальных уравнений

Система дифференциальных уравнений называется линейной, если она линейна относительно неизвестных функций и их производных, входящих в уравнение. Система n линейных уравнений первого порядка, записанная в нормальной форме, имеет вид

или, в матричной форме,

Теорема:

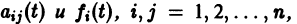
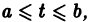
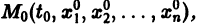
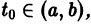
Если все функции непрерывны на отрезке то в достаточно малой окрестности каждой точки где выполнены условия теоремы существования и единственности решения задачи Коши, следовательно, через каждую такую точку проходит единственная интегральная кривая системы (1).

Действительно, в таком случае правые части системы (1) непрерывны по совокупности аргументов t, и их частные производные по ограничены, так как эти производные равны непрерывным на отрезке [а,b] коэффициентам

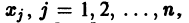
Введем линейный оператор

Тогда система (2) запишется в виде

Если матрица F — нулевая, т. е. 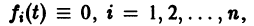на интервале (а,b), то система (2) называется линейной однородной и имеет вид

Приведем некоторые теоремы, устанавливающие свойства решений линейных систем.

Теорема:

Если X(t) является решением линейной однородной системы

то cX(t), где с — произвольная постоянная, является решением той же системы.

Теорема:

двух решений 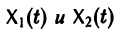однородной линейной системы уравнений является решением той же системы.

Следствие:

с произвольными постоянными коэффициентами сi решений 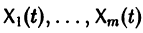линейной однородной системы дифференциальных уравнений

является решением той же системы.

Теорема:

Если 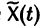есть решение линейной неоднородной системы

a Xo(t) — решение соответствующей однородной системы

будет решением неоднородной системы

Действительно, по условию,

Пользуясь свойством аддитивности оператора 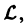получаем

Это означает, что сумма 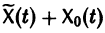есть решение неоднородной системы уравнений

Определение:

называются линейно зависимыми на интервале a

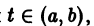
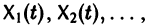
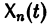
при причем по крайней мере одно из чисел аi, не равно нулю. Если тождество (5) справедливо только при то векторы называются линейно независимыми на (а, b).

Заметим, что одно векторное тождество (5) эквивалентно n тождествам:

называется определителем Вронского системы векторов

Определение:

Пусть имеем линейную однородную систему

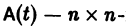
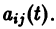
где матрица с элементами Система n решений

линейной однородной системы (6), линейно независимых на интервале а

с непрерывными на отрезке коэффициентами является линейная комбинация п линейно независимых на интервале а

() — произвольные постоянные числа).

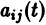
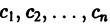
Пример:

имеет, как нетрудно проверить, решения

Эти решения линейно независимы, так как определитель Вронского отличен от нуля:

Общее решение системы имеет вид

(с1, с2 — произвольные постоянные).

Фундаментальная матрица

Квадратная матрица

столбцами которой являются линейно независимые решения 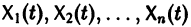системы (6), называется фундаментальной матрицей этой системы. Нетрудно проверить, что фундаментальная матрица удовлетворяет матричному уравнению

Если Х(t) — фундаментальная матрица системы (6), то общее решение системы можно представить в виде

— постоянная матрица-столбец с произвольными элементами. Полагая в (7) t = t0, имеем

Матрица 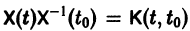называется матрицей Коши. С ее помощью решение системы (6) можно представить так:

Теорема:

О структуре общего решения линейной неоднородной системы дифференциальных уравнений. Общее решение в области 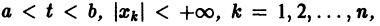линейной неоднородной системы дифференциальных уравнений

с непрерывными на отрезке коэффициентами aij(t) и правыми частями fi(t) равно сумме общего решения

соответствующей однородной системы и какого-нибудь частного решения 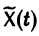неоднородной системы (2):

Метод вариации постоянных

Если известно общее решение линейной однородной системы (6), то частное решение неоднородной системы можно находить методом вариации постоянных (метод Лагранжа).

есть общее решение однородной системы (6), тогда

причем решения Xk(t) линейно независимы.

Будем искать частное решение неоднородной системы

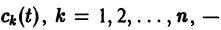
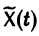
где неизвестные функции от t. Дифференцируя по t, имеем

Подставляя 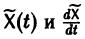в (2), получаем

то для определения 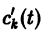получаем систему

или, в развернутом виде,

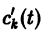
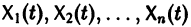
Система (10) есть линейная алгебраическая система относительно определителем которой является определитель Вронского W(t) фундаментальной системы решений . Этот определитель отличен от нуля всюду на интервале a

где 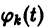— известные непрерывные функции. Интегрируя последние соотношения, находим

Подставляя эти значения 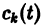в (9), находим частное решение системы (2)

(здесь под символом 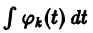понимается одна из первообразных для функции

Системы линейных дифференциальных уравнений с постоянными коэффициентами

Рассмотрим линейную систему дифференциальных уравнений

в которой все коэффициенты 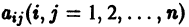— постоянные. Чаще всего такая система интегрируется сведением ее к одному уравнению более высокого порядка, причем это уравнение будет также линейным с постоянными коэффициентами. Другой эффективный метод интегрирования систем с постоянными коэффициентами — метод преобразования Лапласа.

Мы рассмотрим еще метод Эйлера интегрирования линейных однородных систем дифференциальных уравнений с постоянными коэффициентами. Он состоит в следующем.

Метод Эйлера

Будем искать решение системы

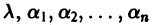
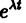
где — постоянные. Подставляя Xk в форме (2) в систему (1), сокращая на и перенося все члены в одну часть равенства, получаем систему

Для того, чтобы эта система (3) линейных однородных алгебраических уравнений с n неизвестными имела нетривиальное решение, необходимо и достаточно, чтобы ее определитель был равен нулю:

Уравнение (4) называется характеристическим. В его левой части стоит многочлен относительно степени n. Из этого уравнения определяются те значения , при которых система (3) имеет нетривиальные решения . Если все корни характеристического уравнения (4) различны, то, подставляя их по очереди в систему (3), находим соответствующие им нетривиальные решения этой системы n, следовательно, находим п решений исходной системы дифференциальных уравнений (1) в виде

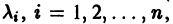
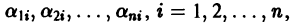
где второй индекс указывает номер решения, а первый — номер неизвестной функции. Построенные таким образом п частных решений линейной однородной системы (1)

образуют, как можно проверить, фундаментальную систему решений этой системы.

Следовательно, общее решение однородной системы дифференциальных уравнений (1) имеет вид

где произвольные постоянные.

Случай, когда характеристическое уравнение имеет кратные корни, мы рассматривать не будем.

Пример:

Ищем решение в виде

имеет корни

Система (3) для определения a1, а2 выглядит так:

Подставляя в (*) 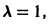получаем

откуда а21 = а11. Следовательно,

Полагая в 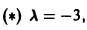находим a22 = — a12, поэтому

Общее решение данной системы:

Матричный метод

Изложим еще матричный метод интегрирования однородной системы (1). Запишем систему (1) в виде

матрица с постоянными действительными элементами

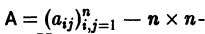
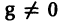
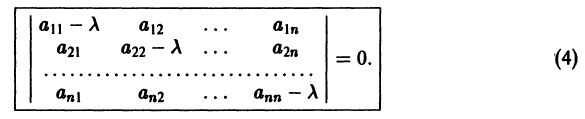
Напомним некоторые понятия из линейной алгебры. Вектор называется собственным вектором матрицы А, если

Число называется собственным значением матрицы А, отвечающим собственному вектору g, и является корнем характеристического уравнения

где I — единичная матрица.

Будем предполагать, что все собственные значения матрицы А различны. В этом случае собственные векторы g1, g2, …gn линейно независимы и существует матрица Т, приводящая матрицу А к диагональному виду, т. е. такая, что

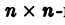
Столбцами матрицы Т являются координаты собственных векторов g1, g2 …, gn матрицы А.

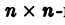
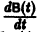
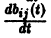
Введем еще следующие понятия. Пусть В(t) — матрица, элементы которой суть функции аргумента t, определенные на множестве . Матрица В(t) называется непрерывной на , если непрерывны на все ее элементы . Матрица В(t) называется дифференцируемой на , если дифференцируемы на все элементы этой матрицы. При этом производной матрицы называется матрица, элементами которой являются производные у соответствующих элементов матрицы В(t).

Пусть B(t) — n х n-матрица,

— вектор-столбец. Учитывая правила алгебры матриц, непосредственной проверкой убеждаемся в справедливости формулы

В частности, если В — постоянная матрица, то

так как 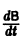есть нуль-матрица.

Теорема:

Если собственные значения матрицы А различны, то общее решение системы (7) имеет вид

где g1, g2,…, gn — собственные векторы-столбцы матрицы А, произвольные постоянные числа.

Введем новый неизвестный вектор-столбец Y(t) по формуле

где Т — матрица, приводящая матрицу А к диагональному виду. Подставляя X(t) из (11) в (7), получим систему

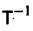
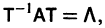
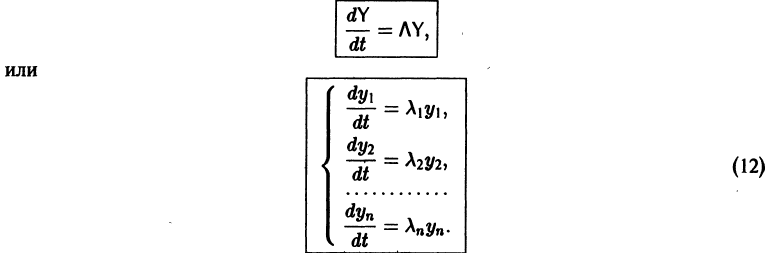
Умножая обе части последнего соотношения слева на и учитывая, что придем к системе

Мы получили систему из n независимых уравнений, которая без труда интегрируется:

Здесь 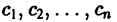— произвольные постоянные числа.

Вводя единичные n-мерные векторы-столбцы

решение Y(t) можно представить в виде

В силу (11) Х(t) = TY(t). Так как столбцы матрицы Т есть собственные векторы матрицы 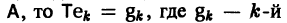собственный вектор матрицы А. Поэтому, подставляя (13) в (11), получим формулу (10):

Таким образом, если матрица А системы дифференциальных уравнений (7) имеет различные собственные значения, для получения общего решения этой системы:

1) находим собственные значения матрицы как корни алгебраического уравнения

2) находим все собственные векторы g1, g2,…, gn;

3) выписываем общее решение системы дифференциальных уравнений (7) по формуле (10).

Пример:

Матрица А системы имеет вид

1) Составляем характеристическое уравнение

Корни характеристического уравнения

2) Находим собственные векторы

Для = 4 получаем систему

откуда g11 = g12, так что

Аналогично для = 1 находим

3) Пользуясь формулой (10), получаем общее решение системы дифференциальных уравнений

Корни характеристического уравнения могут быть действительными и комплексными. Так как по предположению коэффициенты 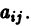системы (7) действительные, то характеристическое уравнение

будет иметь действительные коэффициенты. Поэтому наряду с комплексным корнем оно будет иметь и корень *, комплексно сопряженный с . Нетрудно показать, что если g — собственный вектор, отвечающий собственному значению , то * — тоже собственное значение, которому отвечает собственный вектор g*, комплексно сопряженный с g.

При комплексном решение

системы (7) также будет комплексным. Действительная часть

этого решения являются решениями системы (7). Собственному значению * будет отвечать пара действительных решений X1 и -Х2, т. е. та же пара, что и для собственного значения . Таким образом, паре , * комплексно сопряженных собственных значений отвечает пара действительных решений системы (7) дифференциальных уравнений.

Пусть — действительные собственные значения, — комплексные собственные значения. Тогда всякое действительное решение системы (7) имеет вид

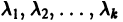
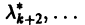
где сi — произвольные постоянные.

Пример:

1) Характеристическое уравнение системы

Его корни

2) Собственные векторы матриц

3) Решение системы

где а1, а2 — произвольные комплексные постоянные.

Найдем действительные решения системы. Пользуясь формулой Эйлера

Следовательно, всякое действительное решение системы имеет

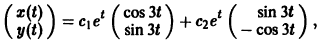
где с1, с2 — произвольные действительные числа.

Видео:ДУ Линейные системыСкачать

Понятие о системах дифференциальных уравнений

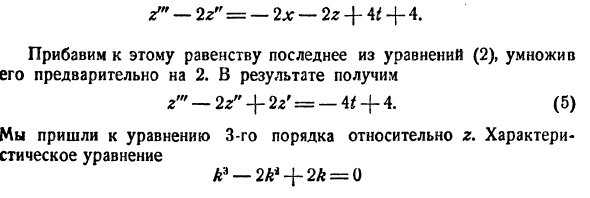
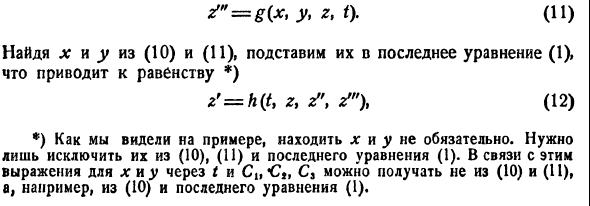
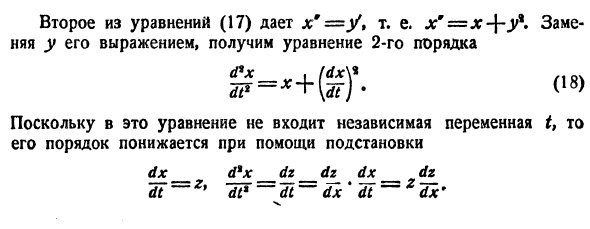
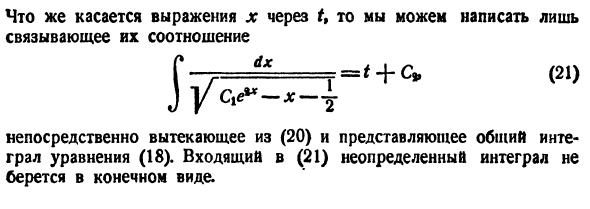
Решение заданий и задач по предметам:

Дополнительные лекции по высшей математике:

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

Видео:Овчинников А. В. - Линейная алгебра - Собственные значения и собственные векторы линейного оператораСкачать

Как решить систему дифференциальных уравнений?

Системы дифференциальных уравнений – традиционный «хедлайнер» темы диффуров, то есть, системы ДУ обычно изучаются в последнюю очередь. Всё начинается и всё заканчивается. Первый урок по теме назывался Дифференциальные уравнения первого порядка. Примеры решений, и вот настала пора заключительной статьи. Слава те Даже прослезился. …Впрочем, это, конечно же, оказалось неправдой – через некоторое время я просто не смог себя сдержать и разобрал задачи с диффурами, а также некоторые методы приближённых вычислений =)

Предполагается, что читатель уже неплохо умеет решать дифференциальные уравнения, в частности, однородные уравнения второго порядка и неоднородные уравнения второго порядка с постоянными коэффициентами. В системах дифференциальных уравнений нет ничего сложного, и если вы уверенно расправляетесь с вышеуказанными типами уравнений, то освоение систем не составит особого труда.

Существуют два основных типа систем дифференциальных уравнений:

– Линейные однородные системы дифференциальных уравнений
– Линейные неоднородные системы дифференциальных уравнений

И два основных способа решения системы дифференциальных уравнений:

– Метод исключения. Суть метода состоит в том, что в ходе решения система ДУ сводится к одному дифференциальному уравнению.

– С помощью характеристического уравнения (так называемый метод Эйлера).

В подавляющем большинстве случаев систему дифференциальных уравнений требуется решить первым способом. Второй способ в условиях задач встречается значительно реже, за всю мою практику я решил им от силы 10-20 систем. Но и его тоже коротко рассмотрим в последнем параграфе данной статьи.

Сразу прошу прощения за теоретическую неполноту материала, но зато я включил в урок только те задания, которые реально могут встретиться на практике. То, что выпадает метеоритным дождем раз в пятилетку, вы вряд ли здесь найдете, и с такими нежданчиками следует обратиться к специализированным кирпичам по диффурам.

Видео:15. Однородная система линейных уравнений / фундаментальная система решенийСкачать

Линейные однородные системы дифференциальных уравнений

Простейшая однородная система дифференциальных уравнений имеет следующий вид:

Собственно, почти все практические примеры такой системой и ограничиваются =)

– это числа (числовые коэффициенты). Самые обычные числа. В частности, один, несколько или даже все коэффициенты могут быть нулевыми. Но такие подарки подкидывают редко, поэтому числа чаще всего не равны нулю.

и – это неизвестные функции. В качестве независимой переменной выступает переменная – это «как бы икс в обычном дифференциальном уравнении».

и – первые производные неизвестных функций и соответственно.

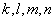
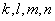
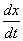
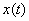
Что значит решить систему дифференциальных уравнений?

Это значит, найти такие функции 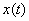и , которые удовлетворяют и первому и второму уравнению системы. Как видите, принцип очень похож на обычные системы линейных уравнений. Только там корнями являются числа, а здесь – функции.

Найденный ответ записывают в виде общего решения системы дифференциальных уравнений:

В фигурных скобках! Эти функции находятся «в одной упряжке».

Для системы ДУ можно решить задачу Коши, то есть, найти частное решение системы, удовлетворяющее заданным начальным условиям. Частное решение системы тоже записывают с фигурными скобками.

Более компактно систему можно переписать так:

Но в ходу традиционно более распространен вариант решения с производными, расписанными в дифференциалах, поэтому, пожалуйста, сразу привыкайте к следующим обозначениям:
и – производные первого порядка;
и – производные второго порядка.

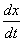
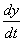
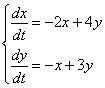
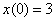
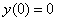
Решить задачу Коши для системы дифференциальных уравнений с начальными условиями , .

Решение: В задачах чаще всего система встречается с начальными условиями, поэтому почти все примеры данного урока будут с задачей Коши. Но это не важно, поскольку общее решение по ходу дела все равно придется найти.

Решим систему методом исключения. Напоминаю, что суть метода – свести систему к одному дифференциальному уравнению. А уж дифференциальные уравнения, надеюсь, вы решаете хорошо.

Алгоритм решения стандартен:

1) Берем второе уравнение системы 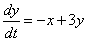и выражаем из него :

Данное уравнение нам потребуется ближе к концу решения, и я помечу его звёздочкой. В учебниках, бывает, натыкают 500 обозначений, а потом ссылаются: «по формуле (253)…», и ищи эту формулу где-нибудь через 50 страниц сзади. Я же ограничусь одной единственной пометкой (*).

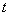
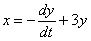
2) Дифференцируем по обе части полученного уравнения :

Со «штрихами» процесс выглядит так:

Важно, чтобы этот простой момент был понятен, далее я не буду на нём останавливаться.

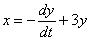
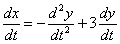
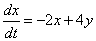
3) Подставим и в первое уравнение системы :

И проведём максимальные упрощения:

Получено самое что ни на есть обычное однородное уравнение второго порядка с постоянными коэффициентами. Со «штрихами» оно записывается так: .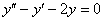

Составим и решим характеристическое уравнение: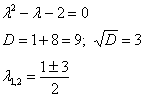

– получены различные действительные корни, поэтому:
.

Одна из функций найдена, пол пути позади.

Да, обратите внимание, что у нас получилось характеристическое уравнение с «хорошим» дискриминантом, а значит, мы ничего не напутали в подстановке и упрощениях.

4) Идём за функцией . Для этого берём уже найденную функцию и находим её производную. Дифференцируем по :

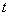
Подставим и в уравнение (*):

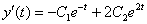
Или короче:

5) Обе функции найдены, запишем общее решение системы:

6) Найдем частное решение, соответствующее начальным условиям , :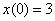

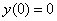
Здесь из первого уравнения я почленно вычел второе уравнение, более подробно о методе можно прочитать в статье Как решить систему линейных уравнений?

Ответ: частное решение:

Полученный ответ достаточно легко проверить, проверку осуществим в три шага:

1) Проверяем, действительно ли выполняются начальные условия , :

Оба начальных условия выполняются.

2) Проверим, удовлетворяет ли найденный ответ первому уравнению системы .

Берём из ответа функцию 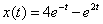и находим её производную:

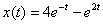
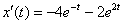
Подставим , и в первое уравнение системы:

Получено верное равенство, значит, найденный ответ удовлетворяет первому уравнению системы.

3) Проверим, удовлетворяет ли ответ второму уравнению системы

Берём из ответа функцию и находим её производную:

Подставим , и во второе уравнение системы:

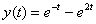
Получено верное равенство, значит, найденный ответ удовлетворяет второму уравнению системы.

Проверка завершена. Что проверено? Проверено выполнение начальных условий. И, самое главное, показан тот факт, что найденное частное решение 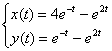удовлетворяет каждому уравнению исходной системы .

Аналогично можно проверить и общее решение , проверка будет даже еще короче, так как не надо проверять выполнение начальных условий.

Теперь вернемся к прорешанной системе и зададимся парой вопросов. Решение начиналось так: мы взяли второе уравнение системы и выразили из него . А можно ли было выразить не «икс», а «игрек»? Если мы выразим , то это нам ничего не даст – в данном выражении справа есть и «игрек» и «икс», поэтому нам не удастся избавиться от переменной и свести решение системы к решению одного дифференциального уравнения.

Вопрос второй. Можно ли было начать решение не со второго, а с первого уравнения системы? Можно. Смотрим на первое уравнение системы: . В нём у нас два «икса» и один «игрек», поэтому необходимо выразить строго «игрек» через «иксы»: . Далее находится первая производная: . Потом следует подставить и во второе уравнение системы. Решение будет полностью равноценным, с тем отличием, что сначала мы найдем функцию , а затем .

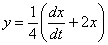
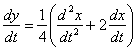
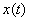
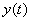
И как раз на второй способ будет пример для самостоятельного решения:

Найти частное решение системы дифференциальных уравнений, удовлетворяющее заданным начальным условиям.

В образце решения, который приведен в конце урока, из первого уравнения выражен и вся пляска начинается от этого выражения. Попытайтесь самостоятельно по пунктам провести зеркальное решение, не заглядывая в образец.

Можно пойти и путём Примера №1 – из второго уравнения выразить (заметьте, что выразить следует именно «икс»). Но этот способ менее рационален, по той причине, что у нас получилась дробь, что не совсем удобно.

Видео:Собственные значения и собственные векторыСкачать

Линейные неоднородные системы дифференциальных уравнений

Практически то же самое, только решение будет несколько длиннее.

Неоднородная система дифференциальных уравнений, которая в большинстве случаев может встретиться вам в задачах, имеет следующий вид:

По сравнению с однородной системой в каждом уравнении дополнительно добавляется некоторая функция, зависящая от «тэ». Функции 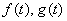могут быть константами (причем, по крайне мере одна из них не равна нулю), экспонентами, синусами, косинусами и т.д.

Найти частное решение системы линейных ДУ, соответствующее заданным начальным условиям

Решение: Дана линейная неоднородная система дифференциальных уравнений, в качестве «добавок» выступают константы. Используем метод исключения, при этом сам алгоритм решения полностью сохраняется. Для разнообразия я начну как раз с первого уравнения.

1) Из первого уравнения системы выражаем:

Это важная штуковина, поэтому я её снова замаркирую звёздочкой. Скобки лучше не раскрывать, зачем лишние дроби?

И еще раз заметьте, что из первого уравнения выражается именно «игрек» – через два «икса» и константу.

2) Дифференцируем по обе части:

Константа (тройка) исчезла, ввиду того, что производная константы равна нулю.

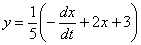
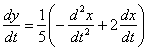
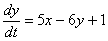
3) Подставим и во второе уравнение системы :

Сразу после подстановки целесообразно избавиться от дробей, для этого каждую часть уравнения умножаем на 5:

Теперь проводим упрощения:

В результате получено линейное неоднородное уравнение второго порядка с постоянными коэффициентами. Вот, по сути, и всё отличие от решения однородной системы уравнений, разобранного в предыдущем параграфе.

Примечание: Тем не менее, в неоднородной системе иногда может получиться и однородное уравнение.

Найдем общее решение соответствующего однородного уравнения:

Составим и решим характеристическое уравнение: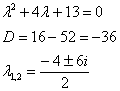

– получены сопряженные комплексные корни, поэтому:
.

Корни характеристического уравнения опять получились «хорошими», значит, мы на верном пути.

Частное решение неоднородного уравнения ищем в виде .
Найдем первую и вторую производную:

Подставим в левую часть неоднородного уравнения:

Таким образом:

Следует отметить, что частное решение легко подбирается устно, и вполне допустимо вместо длинных выкладок написать: «Очевидно, что частное решение неоднородного уравнения: ».

В результате:

4) Ищем функцию . Сначала находим производную от уже найденной функции :

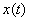
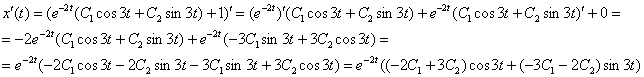
Не особо приятно, но подобные производные в диффурах приходится находить часто.

Шторм в самом разгаре, и сейчас будет девятый вал. Привяжите себя канатом к палубе.

Подставим
и в уравнение (*):

5) Общее решение системы:

6) Найдем частное решение, соответствующее начальным условиям :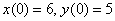

Окончательно, частное решение:

Вот видите, какая история со счастливым концом, теперь можно безбоязненно плавать на шлюпках по безмятежному морю под ласковым солнцем.

Ответ: частное решение:

Кстати, если начать решать эту систему со второго уравнения, то вычисления получатся заметно проще (можете попробовать), но многие посетители сайта просили разбирать и более трудные вещи. Как тут откажешь? =) Пусть будут и более серьезные примеры.

Пример проще для самостоятельного решения:

Найти частное решение линейной неоднородной системы дифференциальных уравнений, соответствующее заданным начальным условиям

Данная задача решена мной по образцу Примера №1, то есть, из второго уравнения выражен «икс». Решение и ответ в конце урока.

В рассмотренных примерах я не случайно использовал различные обозначения, применял разные пути решения. Так, например, производные в одном и том же задании записывались тремя способами: 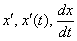. В высшей математике не нужно бояться всяких закорючек, главное, понимать алгоритм решения.

Видео:Видеоурок "Системы дифференциальных уравнений"Скачать

Метод характеристического уравнения (метод Эйлера)

Как уже отмечалось в начале статьи, с помощью характеристического уравнения систему дифференциальных уравнений требуют решить довольно редко, поэтому в заключительном параграфе я рассмотрю всего лишь один пример.

Дана линейная однородная система дифференциальных уравнений

Найти общее решение системы уравнений с помощью характеристического уравнения

Решение: Смотрим на систему уравнений и составляем определитель второго порядка: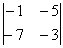

По какому принципу составлен определитель, думаю, всем видно.

Составим характеристическое уравнение, для этого из каждого числа, которое располагается на главной диагонали, вычитаем некоторый параметр :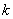

На чистовике, естественно, сразу следует записать характеристическое уравнение, я объясняю подробно, по шагам, чтобы было понятно, что откуда взялось.

Раскрываем определитель:

И находим корни квадратного уравнения:

Если характеристическое уравнение имеет два различных действительных корня, то общее решение системы дифференциальных уравнений имеет вид:

Коэффициенты в показателях экспонент 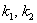нам уже известны, осталось найти коэффициенты

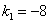
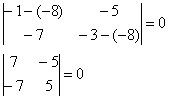
1) Рассмотрим корень и подставим его в характеристическое уравнение:

(эти два определителя на чистовике тоже можно не записывать, а сразу устно составить нижеприведенную систему)

Из чисел определителя составим систему двух линейных уравнений с двумя неизвестными:

Из обоих уравнений следует одно и то же равенство:

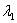
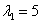
Теперь нужно подобрать наименьшее значение , такое, чтобы значение было целым. Очевидно, что следует задать . А если , то

2) Всё аналогично. Рассмотрим корень 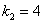и устно подставим его в характеристическое уравнение:

Из чисел определителя составим систему:

Из обоих уравнений следует равенство:

Подбираем наименьшее значение , таким образом, чтобы значение было целым. Очевидно, что .

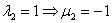
Все четыре коэффициента найдены, осталось их подставить в общую формулу

Ответ: общее решение:

Для тренировки можете с помощью характеристического уравнения решить Пример 1 (подходит только он) данного урока, тем более, есть известный ответ.

Что делать, когда корни характеристического уравнения являются кратными или сопряженными комплексными? В своей коллекции искал-искал примеры, да так и не нашел. Потом стал вспоминать, а встречались ли мне такие уравнения вообще? Да, встречалось. Один раз много лет назад.

Но что делать, если вам таки попался раритет? Порекомендую неплохую, вполне доступную книгу по диффурам: М.Л. Краснов, А.И. Киселев, Г.И. Макаренко Дифференциальные уравнения. Можно прямо выделить мышкой авторов, название книги и скопировать их в поисковик. Лично не закачивал (у меня есть бумажная версия книги), но весь серп забит бесплатными предложениями о закачке. В разделе про системы дифференциальных уравнений рассмотрены все случаи решения системы методом характеристического уравнения (методом Эйлера).

Учитывая крайне низкую вероятность встречи с такими уравнениями, не считаю нужным включать их в урок, при необходимости юзайте рекомендованную мной книгу.

Так же редко встречаются системы из трех дифференциальных уравнений с тремя переменными (вспомнил от силы 2-3 примера из личной практики). Поэтому они тоже здесь отсутствуют, переписывать же единичные примеры из каких-то сторонних источников, смысла вообще не вижу.

Надеюсь, ваше плавание в дифференциальных уравнениях было успешным!

Решения и ответы:

Пример 2: Решение: Выразим из первого уравнения системы :

Дифференцируем по :
.
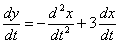
Подставим и во второе уравнение системы:

Характеристическое уравнение:


– кратные действительные корни, поэтому .
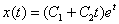
Дифференцируем по :

Подставим и в уравнение (*):

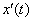
Общее решение системы:

Найдем частное решение, соответствующее заданным начальным условиям:

Ответ: частное решение:

Пример 4: Решение: Выразим их второго уравнения системы:

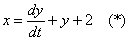
Дифференцируем по :
.
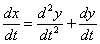
Подставим и в первое уравнение:


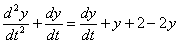
Найдем общее решение соответствующего однородного уравнения: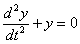

Характеристическое уравнение:

– сопряженные комплексные корни, поэтому общее решение:

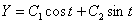
Очевидно, что частное решение неоднородного уравнения: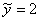
Таким образом: .
Дифференцируем по :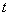

Подставим и в уравнение (*):

Общее решение системы:

Найдем частное решение, соответствующее заданным начальным условиям:

Ответ: частное решение:

Автор: Емелин Александр

(Переход на главную страницу)

Zaochnik.com – профессиональная помощь студентам

cкидкa 15% на первый зaкaз, при оформлении введите прoмoкoд: 5530-hihi5

🎥 Видео

Денисов А. М. - Дифференциальные уравнения. Лекции - Лекция 14Скачать

ОДУ. 4 Системы дифференциальных уравненийСкачать

Асташова И. В. - Дифференциальные уравнения. Часть 2 - Лекция 4Скачать

Асташова И. В. - Дифференциальные уравнения. Часть 2 - Фазовый портретСкачать

Видеоурок "Системы диф. уравнений. Метод Эйлера"Скачать

Асташова И. В. - Дифференциальные уравнения. Часть 2 - Системы дифференциальных уравненийСкачать

Математика без Ху!ни. Метод Гаусса. Совместность системы. Ранг матрицы.Скачать

Особые точки 4 ЗадачаСкачать

Система дифференциальных уравнений векторная формаСкачать

Асташова И. В. - Дифференциальные уравнения. Часть 2 - Решение систем уравненийСкачать