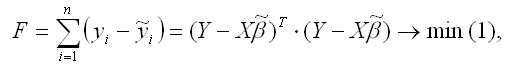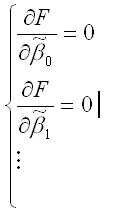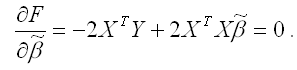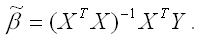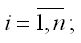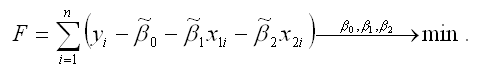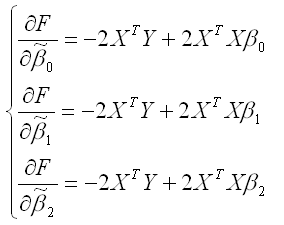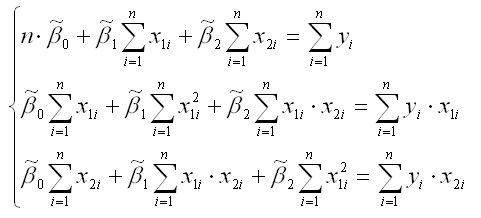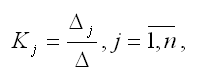В общем виде линейную модель множественной регрессии можно записать следующим образом:
где yi – значение i-ой результативной переменной,
x1i…xmi – значения факторных переменных;
β0…βm – неизвестные коэффициенты модели множественной регрессии;
εi – случайные ошибки модели множественной регрессии.
В результате оценивания данной эконометрической модели определяются оценки неизвестных коэффициентов. Классический подход к оцениванию параметров линейной регрессии основан на методе наименьших квадратов (МНК). Суть метода наименьших квадратов состоит в том, чтобы найти такой вектор β оценок неизвестных коэффициентов модели, при которых сумма квадратов отклонений (остатков) наблюдаемых значений зависимой переменной у от расчётных значений y˜ (рассчитанных на основании построенной модели регрессии) была бы минимальной.
Матричная форма функционала F метода наименьших квадратов:
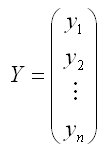

В процессе минимизации функции (1) неизвестными являются только значения коэффициентов β0…βm, потому что значения результативной и факторных переменных известны из наблюдений. Для определения минимума функции (1) необходимо вычислить частные производные этой функции по каждому из оцениваемых параметров и приравнять их к нулю. Результатом данной процедуры будет стационарная система уравнений для функции (1):
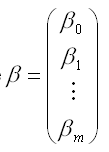
Общий вид стационарной системы уравнений для функции (1):
Решением стационарной системы уравнений будут МНК-оценки неизвестных параметров линейной модели множественной регрессии:
Оценим с помощью метода наименьших квадратов неизвестные параметры линейной модели двухфакторной регрессии:
Чтобы рассчитать оценки неизвестных коэффициентов β0,β1 и β2данной двухфакторной модели регрессии, необходимо минимизировать функционал F вида:
Для определения экстремума функции нескольких переменных, частные производные по этим переменным приравниваются к нулю. Результатом данной процедуры будет стационарная система уравнений для модели множественной линейной регрессии с двумя переменными:
В результате элементарных преобразований данной стационарной системы уравнений получим систему нормальных уравнений:
Данная система называется системой нормальных уравнений относительно коэффициентов 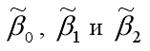
Полученная система нормальных уравнений является квадратной, т. к. количество уравнений равняется количеству неизвестных переменных, поэтому коэффициенты 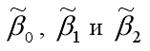
Рассмотрим подробнее метод Крамера решения квадратных систем нормальных уравнений.
Единственное решение квадратной системы линейных уравнений определяется по формуле:
где Δ – основной определитель квадратной системы линейных уравнений;
Δj – определитель, полученный из основного определителя путём замены j-го столбца на столбец свободных членов.
При использовании метода Крамера возможно возникновение следующих ситуаций:
1) если основной определитель системы Δ равен нулю и все определители Δj также равны нулю, то данная система имеет бесконечное множество решений;
2) если основной определитель системы Δ равен нулю и хотя бы один из определителей Δj также равен нулю, то система решений не имеет.
- Множественная линейная регрессия. Улучшение модели регрессии
- Понятие множественной линейной регрессии
- Уравнение множественной линейной регрессии и метод наименьших квадратов
- МНК-оценка коэффиентов уравнения множественной регрессии в скалярном виде
- МНК-оценка коэффиентов уравнения множественной регрессии в матричном виде
- Построение наилучшей (наиболее качественной) модели множественной линейной регрессии
- Оценка качества модели множественной линейной регрессии в целом
- Анализ значимости коэффициентов модели множественной линейной регрессии
- Исключение резко выделяющихся наблюдений
- Исключение незначимых переменных из модели
- Нелинейные модели для сравнения
- Применение пошаговых алгоритмов включения и исключения переменных
- Выбор самой качественной модели множественной линейной регрессии
- Оценка параметров линейного регрессионного уравнения
- 📸 Видео
Видео:Метод наименьших квадратов. Линейная аппроксимацияСкачать

Множественная линейная регрессия. Улучшение модели регрессии
Видео:Метод наименьших квадратов, урок 1/2. Линейная функцияСкачать
Понятие множественной линейной регрессии
Множественная линейная регрессия — выраженная в виде прямой зависимость среднего значения величины Y от двух или более других величин X 1 , X 2 , . X m . Величину Y принято называть зависимой или результирующей переменной, а величины X 1 , X 2 , . X m — независимыми или объясняющими переменными.
В случае множественной линейной регрессии зависимость результирующей переменной одновременно от нескольких объясняющих переменных описывает уравнение или модель

где 

Функция множественной линейной регрессии для выборки имеет следующий вид:

где 

Видео:11 4 Применение МНК к решению систем линейных уравненийСкачать

Уравнение множественной линейной регрессии и метод наименьших квадратов
Коэффициенты модели множественной линейной регресии, так же, как и для парной линейной регрессии, находят при помощи метода наименьших квадратов.
Разумеется, мы будем изучать построение модели множественной регрессии и её оценивание с использованием программных средств. Но на экзамене часто требуется привести формулы МНК-оценки (то есть оценки по методу наименьших квадратов) коэффициентов уравнения множественной линейной регрессии в скалярном и в матричном видах.
МНК-оценка коэффиентов уравнения множественной регрессии в скалярном виде
Метод наименьших квадратов позволяет найти такие значения коэффициентов, что сумма квадратов отклонений будет минимальной. Для нахождения коэффициентов решается система нормальных уравнений
Решение системы можно получить, например, методом Крамера:

Определитель системы записывается так:
МНК-оценка коэффиентов уравнения множественной регрессии в матричном виде
Данные наблюдений и коэффициенты уравнения множественной регрессии можно представить в виде следующих матриц:
Формула коэффициентов множественной линейной регрессии в матричном виде следующая:

где 


Решая это уравнение, мы получим матрицу-столбец b, элементы которой и есть коэффициенты уравнения множественной линейной регрессии, для нахождения которых и был изобретён метод наименьших квадратов.
Видео:Математика это не ИсламСкачать

Построение наилучшей (наиболее качественной) модели множественной линейной регрессии
Пусть при обработке данных некоторой выборки в пакете программных средств STATISTICA получена первоначальная модель множественной линейной регрессии. Предстоит проанализировать полученную модель и в случае необходимости улучшить её.
Качество модели множественной линейной регрессии оценивается по тем же показателям качества, что и в случае модели парной линейной регрессии: коэффициент детерминации 

Важный показатель качества модели линейной регрессии — проверка на выполнение требований Гаусса-Маркова к остаткам. В качественной модели линейной регрессии выполняются все условия Гаусса-Маркова:
- условие 1: математическое ожидание остатков равно нулю для всех наблюдений ( ε(e i ) = 0 );
- условие 2: теоретическая дисперсия остатков постоянна (равна константе) для всех наблюдений ( σ²(e i ) = σ²(e i ), i = 1, . n );
- условие 3: отсутствие систематической связи между остатками в любых двух наблюдениях;
- условие 4: отсутствие зависимости между остатками и объясняющими (независимыми) переменными.
В случае выполнения требований Гаусса-Маркова оценка коэффициентов модели, полученная методом наименьших квадратов является
Затем необходимо провести анализ значимости отдельных переменных модели множественной линейной регрессии с помощью критерия Стьюдента.
В случае наличия резко выделяющихся наблюдений (выбросов) нужно последовательно по одному исключить их из модели и проанализировать наличие незначимых переменных в модели и, в случае необходимости исключить их из модели по одному.
В исследованиях поведения человека, как и во многих других, чтобы они претендовали на объективность, важно не только установить зависимость между факторами, но и получить все необходимые статистические показатели для результата проверки соответствующей гипотезы.
Кроме того, требуется на основе тех же данных построить две нелинейные модели регрессии — с квадратами двух наиболее значимых переменных и с логарифмами тех же наиболее значимых переменных. Они также будут сравниваться с линейными моделями, полученных на разных шагах.
Также требуется построить модели с применением пошаговых процедур включения (FORWARD STEPWISE) и исключения (BACKWARD STEPWISE).
Все полученные модели множественной регрессии нужно сравнить и выбрать из них наилучшую (наиболее качественную). Теперь разберём перечисленные выше шаги последовательно и на примере.
Видео:Метод наименьших квадратовСкачать

Оценка качества модели множественной линейной регрессии в целом
Пример. Задание 1. Получено следующее уравнение множественной линейной регрессии:
и следующие показатели качества описываемой этим уравнением модели:
 | adj. | RSS | SEE | F | p-level |
| 0,426 | 0,279 | 2,835 | 1,684 | 2,892 | 0,008 |
Сделать вывод о качестве модели в целом.
Ответ. По всем показателям модель некачественная. Значение 

Для анализа на выполнение условий Гаусса-Маркова воспользуемся диаграммой рассеивания наблюдений (для увеличения рисунка щёлкнуть по нему левой кнопкой мыши):
Результаты проверки графика показывают: условие равенства нулю математического ожидания остатков выполняется, а условие на постоянство дисперсии — не выполняется. Достаточно невыполнения хотя бы одного условия Гаусса-Маркова, чтобы заключить, что оценка коэффициентов модели линейной регрессии не является несмещённой, эффективной и состоятельной.
Видео:Решение системы линейных уравнений графическим методом. 7 класс.Скачать

Анализ значимости коэффициентов модели множественной линейной регрессии
С помощью критерия Стьюдента проверяется гипотеза о том, что соответствующий коэффициент незначимо отличается от нуля, и соответственно, переменная при этом коэффициенте имеет незначимое влияние на зависимую переменную. В свою очередь, в колонке p-level выводится вероятность того, что основная гипотеза будет принята. Если значение p-level больше уровня значимости α, то основная гипотеза принимается, иначе – отвергается. В нашем примере установлен уровень значимости α=0,05.
Пример. Задание 2. Получены следующие значения критерия Стьюдента (t) и p-level, соответствующие переменным уравнения множественной линейной регрессии:
| Перем. | Знач. коэф. | t | p-level |
| X1 | 0,129 | 2,386 | 0,022 |
| X2 | -0,286 | -2,439 | 0,019 |
| X3 | -0,037 | -0,238 | 0,813 |
| X4 | 0,15 | 1,928 | 0,061 |
| X5 | 0,328 | 0,548 | 0,587 |
| X6 | -0,391 | -0,503 | 0,618 |
| X7 | -0,673 | -0,898 | 0,375 |
| X8 | -0,006 | -0,07 | 0,944 |
| X9 | -1,937 | -2,794 | 0,008 |
| X10 | -1,233 | -1,863 | 0,07 |
Сделать вывод о значимости коэффициентов модели.
Ответ. В построенной модели присутствуют коэффициенты, которые незначимо отличаются от нуля. В целом же у переменной X8 коэффициент самый близкий к нулю, а у переменной X9 — самое высокое значение коэффициента. Коэффициенты модели линейной регрессии можно ранжировать по мере убывания незначимости с возрастанием значения t-критерия Стьюдента.
Видео:Эконометрика. Линейная парная регрессияСкачать

Исключение резко выделяющихся наблюдений
Пример. Задание 3. Выявлены несколько резко выделяющихся наблюдений (выбросов, то есть наблюдений с нетипичными значениями): 10, 3, 4 (соответствуют строкам исходной таблицы данных). Эти наблюдения следует последовательно исключить из модели и по мере исключения заполнить таблицу с показателями качества модели. Исключили наблюдение 10 — заполнили значение показателей, далее исключили наблюдение 3 — заполнили и так далее. По мере исключения STATISTICA будет выдавать переменные, которые остаются значимыми в модели множественной линейной регрессии — они будут выделены красном цветом. Те, что не будут выделены красным цветом — незначимые переменные и их также нужно внести в соответствующую ячейку таблицы. По завершении исключения выбросов записать уравнение конечной множественной линейной регрессии.
| № | adj. | SEE | F | p- level | незнач. пер. |
| 10 | 0,411 | 2,55 | 2,655 | 0,015 | X3, X4, X5, X6, X7, X8, X10 |
| 3 | 0,21 | 2,58 | 2,249 | 0,036 | X3, X4, X5, X6, X7, X8, X10 |
| 4 | 0,16 | 2,61 | 1,878 | 0,082 | X3, X4, X5, X6, X7, X8, X10 |
Уравнение конечной множественной линейной регрессии:
Случается однако, когда после исключения некоторого наблюдения исключение последующих наблюдений приводит к ухудшению показателей качества модели. Причина в том, что с исключением слишком большого числа наблюдений выборка теряет информативность. Поэтому в таких случаях следует вовремя остановиться.
Видео:Суть метода наименьших квадратов с примерами. Основы эконометрики в RСкачать

Исключение незначимых переменных из модели
Пример. Задание 4. По мере исключения из модели множественной линейной регрессии переменных с незначимыми коэффициентами (получены при выполнении предыдущего задания, занесены в последнюю колонку таблицы) заполнить таблицу с показателями качества модели. Последняя колонка, обозначенная звёздочкой — список переменных, имеющих значимое влияние на зависимую переменную. Эти переменные STATISTICA будет выдавать выделенными красным цветом. По завершении исключения незначимых переменных записать уравнение конечной множественной линейной регрессии.
| Искл. пер. | adj. | SEE | F | p- level | * |
| X3 | 0,18 | 1,71 | 2,119 | 0,053 | X4, X5, X6, X7, X8, X10 |
| X4 | 0,145 | 1,745 | 1,974 | 0,077 | X5, X6, X7, X8, X10 |
| X5 | 0,163 | 2,368 | 2,282 | 0,048 | X6, X7, X8, X10 |
| X6 | 0,171 | 2,355 | 2,586 | 0,033 | X7, X8, X10 |
| X7 | 0,167 | 2,223 | 2,842 | 0,027 | X8, X10 |
| X8 | 0,184 | 1,705 | 3,599 | 0,013 | X10 |
Когда осталась одна переменная, имеющая значимое влияние на зависимую переменную, больше не исключаем переменные, иначе получится, что в модели все переменные незначимы.
Уравнение конечной множественной линейной регрессии после исключения незначимых переменных:
Переменные X1 и X2 в задании 3 не вошли в список незначимых переменных, поэтому они вошли в уравнение конечной множественной линейной регрессии «автоматически».
Видео:Что такое параметр? Уравнения и неравенства с параметром. 7-11 класс. Вебинар | МатематикаСкачать

Нелинейные модели для сравнения
Пример. Задание 5. Построить две нелинейные модели регрессии — с квадратами двух наиболее значимых переменных и с логарифмами тех же наиболее значимых переменных.
Так как в наблюдениях переменных X9 и X10 имеется 0, а натуральный логарифм от 0 вычислить невозможно, то берутся следующие по значимости переменные: X1 и X2.
Полученное уравнение нелинейной регрессии с квадратами двух наиболее значимых переменных:
Показатели качества первой модели нелинейной регрессии:
 | adj. | RSS | SEE | F | p-level |
| 0,17 | 0,134 | 159,9 | 1,845 | 4,8 | 0,0127 |
Вывод: модель некачественная, так как RSS и SEE принимают высокие значения, p-level стремится к нулю, коэффициент детерминации незначимо отличается от нуля.
Полученное уравнение нелинейной регрессии с логарифмами двух наиболее значимых переменных:
Показатели качества второй модели нелинейной регрессии:
 | adj. | RSS | SEE | F | p-level |
| 0,182 | 0,148 | 157,431 | 1,83 | 5,245 | 0 |
Вывод: модель некачественная, так как RSS и SEE принимают высокие значения, p-level стремится к нулю, коэффициент детерминации незначимо отличается от нуля.
Видео:Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

Применение пошаговых алгоритмов включения и исключения переменных
Пример. Задание 6. Настроить пакет STATISTICA для применения пошаговых процедур включения (FORWARD STEPWISE) и исключения (BACKWARD STEPWISE). Для этого в диалоговом окне MULTIPLE REGRESSION указать Advanced Options (stepwise or ridge regression). В поле Method выбрать либо Forward Stepwise (алгоритм пошагового включения), либо Backward Stepwise (алгоритм пошагового исключения). Необходимо настроить следующие параметры:
- в окне Tolerance необходимо установить критическое значение для уровня толерантности (оставить предложенное по умолчанию);
- в окне F-remove необходимо установить критическое значение для статистики исключения (оставить предложенное по умолчанию);
- в окне Display Results необходимо установить режим At each step (результаты выводятся на каждом шаге процедуры).
Построить, как описано выше, модели множественной линейной регрессии автоматически.
В результате применения пошагового алгоритма включения получено следующее уравнение множественной линейной регрессии:
Показатели качества модели нелинейной регрессии, полученной с применением пошаговой процедуры включения:
 | adj. | RSS | SEE | F | p-level |
| 0,41 | 0,343 | 113,67 | 1,61 | 6,11 | 0,002 |
В результате применения пошагового алгоритма исключения получено следующее уравнение множественной линейной регрессии:
Показатели качества модели нелинейной регрессии, полученной с применением пошаговой процедуры исключения:
 | adj. | RSS | SEE | F | p-level |
| 0,22 | 0,186 | 150,28 | 1,79 | 6,61 | 0 |
Видео:Решение систем уравнений методом подстановкиСкачать

Выбор самой качественной модели множественной линейной регрессии
Пример. Задание 7. Сравнить модели, полученные на предыдущих шагах и определить самую качественную.
| Модель | Ручная | Кв. перем. | Лог. перем. | forward stepwise | backward stepwise |
 | 0,255 | 0,17 | 0,182 | 0,41 | 0,22 |
adj. | 0,184 | 0,134 | 0,148 | 0,343 | 0,186 |
| RSS | 122,01 | 159,9 | 157,43 | 113,67 | 150,28 |
| SEE | 1,705 | 1,845 | 1,83 | 1,61 | 1,79 |
| F | 3,599 | 4,8 | 5,245 | 6,11 | 6,61 |
| p-level | 0,013 | 0,0127 | 0 | 0,002 | 0 |
Самая качественная модель множественной линейной регрессии — модель, построенная методом FORWARD STEPWISE (пошаговое включение переменных), так как коэффициент детерминации у неё самый высокий, а RSS и SEE наименьшие в сравнении значений оценок качества других регрессионных моделей.
Видео:Графический способ решения систем уравнений. Алгебра, 9 классСкачать

Оценка параметров линейного регрессионного уравнения
Для оценки параметров регрессионного уравнения наиболее часто используют метод наименьших квадратов (МНК), в основе которого лежит предположение о независимости наблюдений исследуемой совокупности. Сущность данного метода заключается в нахождении параметров модели (α, β), при которых минимизируется сумма квадратов отклонений эмпирических (фактических) значений результативного признака от теоретических, полученных по выбранному уравнению регрессии:
В итоге получаем систему нормальных уравнений:
Эту систему можно записать в виде:
Решая данную систему линейных уравнений с двумя неизвестными получаем оценки наименьших квадратов:
В уравнениях регрессии параметр α показывает усредненное влияние на результативный признак неучтенных факторов, а параметр β – коэффициент регрессии показывает, насколько изменяется в среднем значение результативного признака при увеличении факторного на единицу.
Между линейным коэффициентом корреляции и коэффициентом регрессии существует определенная зависимость, выражаемая формулой:
где – коэффициент регрессии в уравнении связи;
– среднее квадратическое отклонение соответствующего статистически существенного факторного признака.
Имеются следующие данные о размере страховой суммы и страховых возмещений на автотранспортные средства одной из страховых компаний.
Зависимость между размером страховых возмещений и страховой суммой на автотранспорт
Объем страхового возмещения (тыс.долл.), Yi
Стоимость застрахованного автомобиля (тыс.долл.), X i
📸 Видео
ПОСМОТРИ это видео, если хочешь решить систему линейных уравнений! Метод ПодстановкиСкачать

Способы решения систем нелинейных уравнений. 9 класс.Скачать

Построить график ЛИНЕЙНОЙ функции и найти:Скачать

Системы линейных уравнений с параметром.Скачать

Математика | Система уравнений на желтую звездочку (feat Золотой Медалист по бегу)Скачать

МНК линейный тренд в MS ExcelСкачать

Решение системы линейных уравнений с двумя переменными способом подстановки. 6 класс.Скачать

Метод наименьших квадратов. ТемаСкачать