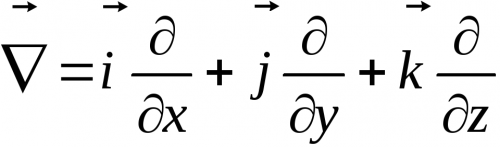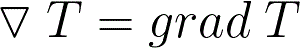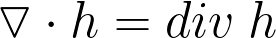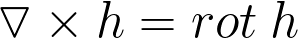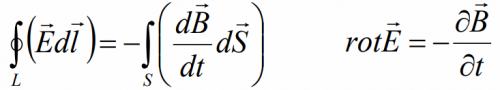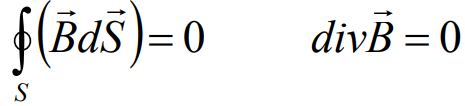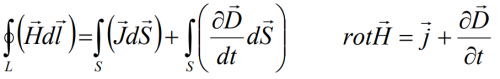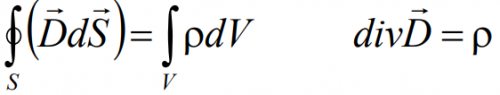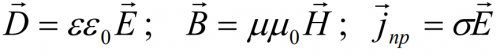Уравнения Максвелла в диэлектрической среде

Уравнения Максвелла в произвольной среде таковы

(1a)

система (1a) замыкается материальными соотношениями . Здесь — векторы электрической и магнитной индукции; — плотность токов проводимости; — плотность электрических зарядов; — величины, характеризующие свойства среды и считающиеся при этом заданными функциями точки, но не времени; — сторонние электродвижущие силы – заданные функции точки и времени.

Заметим, что в приведенном, общепринятом виде (1a) формулировка уравнений принадлежит Герцу (Максвелл уравнения приводил в интегральной форме).

Заметим также, что система (1a) – это постулат, обобщающий все известные до Максвелла явления электричества и магнетизма (Кулон 1785 г. – закон взаимодействия электрических зарядов; Эрстед 1820 г. – магнитное действие тока, существование связи между магнитными и электрическими явлениями; Ампер – все магнитные явления в природе вызваны электрическими токами (теория молекулярных токов Ампера); Фарадей 1831 г. – электромагнитная индукция; и т. д.)

Волновое уравнение. Электромагнитная природа света.

Для интересующих нас в дальнейшем диэлектриков с , система Максвелла принимает вид

(1.1)

.

откуда, если диэлектрическая проницаемость не зависит от времени, получаем

(1.2)

Из векторного анализа известно

,

тогда (1.2) принимает вид

(1.3)

Далее, из условия находим

, (1.4)

В результате, вместо (1.3) имеем

(1.5)

Аналогично, для найдем

(1.6)

В случае однородных диэлектриков , и (1.5),(1.6) принимают вид

(1.7)

Уравнения (1.7) называются волновыми. Их справедливость ограничена лишь требованием однородности среды и отсутствия в ней токов проводимости и свободных зарядов.

К ним относятся как граничные условия на поверхностях разделов сред, так и условия на границах рассматриваемой области пространства. Последние полностью определяются конкретными условиями задачи (например, условия на бесконечности).

Условия на границах разделов для диэлектриков (отсутствие поверхностных зарядов и токов проводимости) эквивалентны уравнениям

, , (1.8)

где индексы 1 и 2 относятся к двум граничащим средам, а t означает любое направление, касательное к поверхности раздела.

Плоские электромагнитные волны

Видео:Физика. Лекция 8. Уравнения Максвелла и электромагнитные волны.Скачать

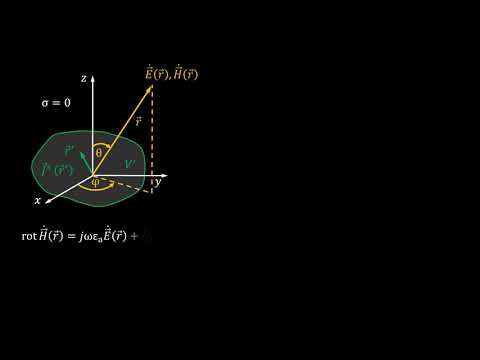
Одним из простейших решений волнового уравнения является плоская волна.

Волна называется плоской, если в любой момент времени во всех точках произвольной плоскости, перпендикулярной направлению распространения волны, векторы поля постоянны. Если этим направлением считать ось z, то компоненты поля плоской, монохроматической волны имеют вид

, , (1.9)

где — частота; векторы , вообще говоря, комплексные и зависят только от координаты z.

Подстановка (1.9) в волновые уравнения (1.7) дает

, , (1.10)

где — волновое число в диэлектрике.

Элементарно решив (1.10), найдем решения волновых уравнений в случае плоских волн в виде

, , (1.11)

каждое из которых представляет собой суперпозицию двух волн, распространяющихся в противоположных направлениях оси z. Здесь — произвольные постоянные интегрирования.

Обычно, в качестве решения рассматривается одна из волн, например,

, . (1.12)

С помощью найденного простейшего решения (1.12) можно продемонстрировать ряд важнейших общих свойств электромагнитных волн.

В частности, если ось z координатной системы не совпадает с направлением распространения волны, дифференцирование векторов поля по координатам сведется к их умножению на величину , где — единичный вектор в направлении распространения. Для однородных диэлектриков из уравнений Максвелла имеем

, , (1.13)

откуда следует, что векторы и перпендикулярны к , т. е. плоские электромагнитные волны – суть поперечные волны.

По аналогии, дифференцирование векторов поля по t сводится к их умножению на . В частности, из второго уравнения Максвелла (1.1) получаем

,

или, с учетом ,

. (1.14)

Последнее означает, что векторы и взаимно перпендикулярны, а три взаимно перпендикулярных вектора , и образуют правовинтовую систему.

Из (1.14) следует также, что , т. е. отношение числовых значений векторов и от времени не зависит, т. е. эти векторы обладают одинаковыми фазами и изменяются синхронно.

Всегда следует помнить, что физический смысл компонент поля, записанных в комплексной форме (см., например, запись (1.12)), несут лишь действительные части этих выражений. При этом каждая из декартовых компонент электрического и магнитного векторов поля плоской, монохроматической волны имеет вид

a>0. (1.15)

Здесь обозначает переменную часть фазового множителя, т. е.

, (1.16)

— направление распространения волны; — постоянная часть этого множителя.

Совместим ось z c . Тогда, в силу поперечности волны отличными от нуля будут только x — и y-компоненты векторов. Исследуем характер кривой, которую конец электрического (или магнитного) вектора описывает в произвольной точке пространства. Эта кривая – геометрическое место точек с координатами

(1.17)

a) Эллиптическая поляризация

После несложных математических операций исключим из (1.17) и получим

, (1.18)

где .

В аналитической геометрии показывается, что (1.18) представляет собой уравнение конического сечения, а более конкретно – уравнение эллипса. Этот эллипс вписан в прямоугольник, стороны которого параллельны координатным осям и имеют длины и . Таким образом, конец электрического вектора описывает эллипс в любой плоскости, перпендикулярной направлению распространения.

Аналогично показывается, что конец магнитного вектора поля также описывает эллипс, вписанный в прямоугольник со сторонами в раз большими. Последнее следует, в частности, из соотношения (1.14).

Из общих физических соображений следует также различать две возможные эллиптические поляризации в соответствии с направлением, в котором конец электрического вектора описывает эллипс. В литературе сформировалось определение, согласно которому правой поляризация называется, когда наблюдателю, смотрящему навстречу световому лучу, кажется, что конец электрического вектора движется по часовой стрелке. Для левой эллиптической поляризации справедливо обратное.

Поскольку параметры в предыдущем рассмотрении были произвольными, то эллиптическую поляризацию электромагнитных волн следует считать наиболее общим из состояний поляризации. Более частные типы поляризации соответствуют определенным соотношениям между этими параметрами.

b) Линейная и круговая поляризации

Перейдем к рассмотрению частных случаев.

,

то эллипс (1.18) превратится в прямую линию. В самом деле, уравнение (1.18) переходит при этом в

, (1.19)

а конец электрического вектора в прямоугольнике колеблется вдоль одной из его диагоналей.

Иногда эта линейная поляризация называется еще плоской поляризацией. Понятно, что в этой ситуации магнитный вектор также линейно поляризован.

Другим частным случаем эллиптической поляризации является круговая. Переход от эллиптической к круговой поляризации происходит тогда, когда, во-первых, и, во-вторых,

, .

Уравнение (1.18) переходит при этом в уравнение окружности

, (1.20)

где также различают правую и левую поляризации.

Видео:Билеты №32, 33 "Уравнения Максвелла"Скачать

Круговая поляризация иногда называется циркулярной.

Итак, во всех случаях поляризованного света концы векторов поля в каждой точке движутся периодически. В случае же неполяризованного света они движутся совершенно нерегулярно, и такие световые колебания не имеют никаких преимущественных направлений в плоскости, перпендикулярной направлению распространения.

Основные законы оптики – преломление света, отражение, полное внутреннее

Применим теперь найденные выше для плоских волн соотношения к исследованию распространения этих волн при наличии плоской границы, разделяющей два однородных, изотропных диэлектрика, занимающих два полупространства.

В задаче о преломлении волн на границе полубесконечной среды физический смысл имеет решение, основанное на предположении о наличии трех волн: падающей, отраженной и преломленной.

Падающая на границу волна порождает новый волновой процесс.

По определению плоская волна полностью определена, если известно ее поведение во времени в некоторой точке пространства. Вторичные поля, возникающие на границе, будут так же изменяться во времени, как и первичное поле падающей волны. Поэтому переменные части фазовых множителей трех волн в произвольной точке должны быть одинаковыми:

, (1.21)

где — единичные векторы в направлениях падающей, отраженной и преломленной волн; — скорости распростра

нения волн в обеих средах.

Выбрав в качестве границы раздела плоскость z=0, (1.21) запишем в виде

. (1.22)

Равенства должны выполняться для любых значений x и y на границе. Это дает

(1.23)

откуда следует, что все три вектора лежат в одной плоскости с нормалью к границе (в плоскости падения).

Выберем в качестве плоскости падения плоскость xz. Тогда y-компоненты векторов равны нулю, а прочие таковы:

(1.24)

где — углы, которые образуют с осью z (рис. 1).

Из (1.24) и (1.23) имеем

(1.25)

откуда , и из рис. 1 видно, что , т. е. угол падения равен углу отражения. В этом состоит закон отражения.

Из (1.25) следует также

(1.26)

Последнее соотношение вместе с утверждением, что нормаль к преломленной волне лежит в плоскости падения составляет закон преломления (или закон Снеллиуса).

Если > (луч падает из более плотной в менее оптически плотную среду), то из (1.26) видно, что для любого угла падения существует вещественный угол преломления ( воспользуемся им и положим

Тогда (1.27) примет вид

(1.28)

Ясно также, что физический смысл имеет лишь нижний знак перед корнем во втором сомножителе в (1.28).

Из (1.28) следует, и это подтверждается опытным путем, что электромагнитное поле в среде 2 все же не равно нулю. Волна (1.28) представляет собой неоднородную волну, распространяющуюся в плоскости падения вдоль x по поверхности раздела сред и с экспоненциально падающей с ростом z амплитудой. Эта волна не является поперечной, поскольку ее компонента электрического вектора . Эффективная глубина ее проникновения в обе стороны от поверхности раздела сред оказывается порядка длины волны.

1. . Электромагнитные волны. Сов. Радио, 1957.

2. М. Борн, Э. Вольф. Основы оптики. М., Наука, 1970.

Видео:О чем говорят уравнения Максвелла? Видео 1/2Скачать

3. . Основы теории электричества. М., Наука, 1989.

Уравнения Максвелла для электромагнитного поля — основные законы электродинамики

Система уравнений Максвелла обязана своим названием и появлением Джеймсу Клерку Максвеллу, сформулировавшему и записавшему данные уравнения в конце 19 века.

Максвелл Джемс Кларк (1831 — 1879) был известным британским физиком и математиком, профессором Кембриджского университета в Англии.

Он практически объединил в своих уравнениях все накопленные к тому времени экспериментально полученные результаты касательно электричества и магнетизма и придал законам электромагнетизма четкую математическую форму. Основные законы электродинамики (уравнения Максвелла) были сформулированы в 1873 году.

Максвелл развил учение Фарадея об электромагнитном поле в стройную математическую теорию, из которой вытекала возможность волнового распространения электромагнитных процессов. При этом оказалось, что скорость распространения электромагнитных процессов равна скорости света (величина которой была уже известна из опытов).

Это совпадение послужило для Максвелла основанием к тому, чтобы высказать идею об общей природе электромагнитных и световых явлений, т.е. об электромагнитной природе света.

Созданная Джеймсом Максвеллом теория электромагнитных явлений нашла первое подтверждение в опытах Герца, впервые получившего электромагнитные волны.

В итоге эти уравнения сыграли главную роль в формировании точных представлений классической электродинамики. Уравнения Максвелла могут быть записаны в дифференциальной или интегральной форме. Практически они описывают сухим языком математики электромагнитное поле и его связь с электрическими зарядами и токами в вакууме и в сплошных средах. К данным уравнениям можно добавить выражение для силы Лоренца, в этом случае мы получим полную систему уравнений классической электродинамики.

Чтобы понимать некоторые математические символы, использующиеся в дифференциальных формах уравнений Максвелла, для начала определим такую занятную вещь, как оператор набла.

Оператор набла (или оператор Гамильтона) — это векторный дифференциальный оператор, компоненты которого являются частными производными по координатам. Для нашего реального пространства, которое является трехмерным, адекватна прямоугольная система координат, для которой оператор набла определяется следующим образом:

где i, j и k – единичные координатные векторы

Оператор набла, будучи применен к полю тем или иным математическим образом, дает три возможные комбинации. Данные комбинации именуются:

Градиент — вектор, своим направлением указывающий направление наибольшего возрастания некоторой величины, значение которой меняется от одной точки пространства к другой (скалярного поля), а по величине (модулю) равный скорости роста этой величины в этом направлении.

Дивергенция (расхождение) — дифференциальный оператор, отображающий векторное поле на скалярное (то есть, в результате применения к векторному полю операции дифференцирования получается скалярное поле), который определяет (для каждой точки), «насколько расходится входящее и исходящее из малой окрестности данной точки поле», точнее, насколько расходятся входящий и исходящий потоки.

Видео:6.1 Решение уравнений Максвелла с заданным сторонним электрическим током методом ЭД потенциаловСкачать

Ротор (вихрь, ротация) — векторный дифференциальный оператор над векторным полем.

Теперь рассмотрим непосредственно уравнения Максвелла в интегральной (слева) и дифференциальной (справа) формах, содержащие в себе основные законы электрического и магнитного полей, включая электромагнитную индукцию.

Интегральная форма: циркуляция вектора напряженности электрического поля по произвольному замкнутому контуру прямо пропорциональна скорости изменения магнитного потока через площадь, ограниченную этим контуром.

Дифференциальная форма: при всяком изменении магнитного поля возникает вихревое электрическое поле, пропорциональное скорости изменения индукции магнитного поля.

Физический смысл: всякое изменение магнитного поля во времени вызывает появление вихревого электрического поля.

Интегральная форма: поток индукции магнитного поля через произвольную замкнутую поверхность равен нулю. Это означает, что в природе нет магнитных зарядов.

Дифференциальная форма: поток силовых линий индукции магнитного поля из бесконечного элементарного объёма равен нулю, так как поле вихревое.

Физический смысл: источники магнитного поля в виде магнитных зарядов в природе отсутствуют.

Интегральная форма: циркуляция вектора напряженности магнитного поля по произвольному замкнутому контуру прямо пропорциональна суммарному току, пересекающему поверхность, охватываемую этим контуром.

Дифференциальная форма: вокруг любого проводника с током и вокруг любого переменного электрического поля существует вихревое магнитное поле.

Физический смысл: протекание тока проводимости по проводникам и изменения электрического поля во времени приводят к появлению вихревого магнитного поля.

Интегральная форма: поток вектора электростатической индукции через произвольную замкнутую поверхность, охватывающую заряды, прямо пропорционален суммарному заряду, расположенному внутри этой поверхности.

Дифференциальная форма: поток вектора индукции электростатического поля из бесконечного элементарного объема прямо пропорционален суммарному заряду, находящемуся в этом объёме.

Физический смысл: источником электрического поля является электрический заряд.

Система данных уравнений может быть дополнена системой так называемых материальных уравнений, которые характеризуют свойства заполняющей пространство материальной среды:

Видео:Уравнения Максвелла. Вихревое электрическое поле. Ток смещенияСкачать

Если Вам понравилась эта статья, поделитесь ссылкой на неё в социальных сетях. Это сильно поможет развитию нашего сайта!

Не пропустите обновления, подпишитесь на наши соцсети:

§25. Ток смещения и система уравнений Максвелла

Мы установили, что изменяющееся магнитное поле порождает изменяющееся электрическое поле, которое в свою очередь порождает изменяющееся магнитное поле и т. д. В результате образуются сцепленные между собой электрическое и магнитное поля, составляющие электромагнитную волну. Она “отрывается” от зарядов и токов, которые ее породи­ли. Способ существования электромагнитной волны делает невозможным ее неподвижность в пространстве и постоянство напряженности во времени.

Постоянный ток не протекает в цепи с конденсатором, а в случае переменного напряжения в цепи ток протекает через конденсатор. Для постоянного тока конденсатор – разрыв в цепи, а для переменного этого разрыва нет. Поэтому необходимо заключить, что между обкладками конденсатора происходит некоторый процесс, который как бы замыкает ток проводимости. Этот процесс между обкладками конденсатора был назван током смещения. Напряженность поля между обкладками конденсатора . Из граничного условия для вектора следует, что диэлектрическое смещение между обкладками , а сила тока в цепи равна . Тогда

, (25.1)

А значит процессом, замыкающим ток проводимости в цепи, является изменение электрического смещения во времени. Плотность тока

. (25.2)

Существование тока смещения было постулировано Максвеллом в 1864 г. и затем экспериментально подтверждено другими учеными.

Почему скорость изменения вектора смещения называется плотностью тока? Само по себе математическое равенство величины , характеризующей процесс между обкладками конденсатора, т. е. равенство двух величин, относящихся к разным областям пространства и имеющим различную физическую природу, не содержит в себе, вообще говоря, какого-то физического закона. Поэтому называть ”током” можно только формально. Для того чтобы придать этому названию физический смысл, необходимо доказать, что обладает наиболее характерными свойствами тока, хотя и не представляет движения электрических зарядов, подобного току проводимости. Главным свойством тока проводимости является его способность порождать магнитное поле. Поэтому решающим является вопрос о том, порождает ли ток смещения магнитное поле так же, как его порождают ток проводимости, или, более точно, порождает ли величина (25.2) такое же магнитное поле, как равная ей объемная плотность тока проводимости? Максвелл дал утвердительный ответ на этот вопрос. Однако наиболее ярким подтверждением порождения магнитного поля током смещения является существование электромагнитных волн. Если бы ток смещения не создавал магнитного поля, то не могли бы существовать электромагнитные волны.

Уравнение Максвелла с током смещения.

Порождение магнитного поля токами проводимости описывается уравнением

(25.3)

Учитывая порождение поля током смещения, необходимо обобщить это уравнение в виде

(25.4)

Тогда, принимая во внимание (25.2), окончательно получаем уравнение

, (25.5)

Являющееся одним из уравнений Максвелла.

Система уравнений Максвелла.

Полученная в результате обобщения экспериментальных данных, эта система имеет вид:

, (25.6)

Эти уравнения называются полевыми и справедливы при описании всех макроскопических электромагнитных явлений. Учет свойств среды достигается уравнениями

, (25.7)

Называемыми обычно Материальными уравнениями среды. Среды линейны, если и нелинейны если . Материальные уравнения, как правило, имеют вид функционалов.

Рассмотрим физический смысл уравнений.

Видео:Уравнения Максвелла 2021Скачать

Уравнение I выражает закон, по которому магнитное поле порождается токами проводимости и смещения, являющимися двумя возможными источниками магнитного поля. Уравнение II выражает закон электромагнитной индукции и указывает на изменяющееся магнитное поле как на один из возможных источников, порождающих электрическое поле. Вторым источником электрического поля являются электрические заряды (уравнение IV). Уравнение III говорит о том, что в природе нет магнитных зарядов.

Полнота и совместность системы. Единственность решения.

В случае линейной среды можно исключить из полевых уравнений (25.6) величины в результате чего они становятся уравнениями относительно векторов и , т. е. относительно шести неизвестных (у каждого вектора по 3 проекции). С другой стороны число скалярных уравнений в (25.6) равно восьми. Получается, что система состоит из 8 уравнений для 6 неизвестных. Однако в действительности система не переполнена. Это обусловлено тем, что уравнения I и IV, а также II и III имеют одинаковые дифференциальные следствия и поэтому связаны между собой.

Чтобы в этом убедиться возьмем от уравнения II и производную по времени от уравнения III. Получим:

,

Т. е. получили одинаковые дифференциальные следствия. Аналогично возьмем от уравнения I:

.

С из уравнения непрерывности следует, что . Тогда

или . Из IV следует, что

Наличие двух дифференциальных связей и делает систему уравнений Максвелла совместной. Более подробный анализ показывает, что система является полной, а ее решение однозначно при заданных начальных и граничных условиях.

Доказательство единственности решения в общих чертах сводится к следующему. Если имеется два различных решения, то их разность вследствие линейности системы тоже является решением, но при нулевых зарядах и токах и нулевых начальных и граничных условиях. Отсюда, пользуясь выражением для энергии электромагнитного поля и законом сохранения энергии заключаем, что разность решений тождественно равна нулю, т. е. решения одинаковы. Тем самым единственность решения уравнений Максвелла доказана.

📸 Видео

Билет №31 "Ток смещения"Скачать

Урок 383. Вихревое электрическое поле. Ток смещенияСкачать

Вывод уравнений МаксвеллаСкачать

Уравнения Максвелла и соответствующие уравнения Волновой МоделиСкачать

ЧК_МИФ: 4.1.1.ДФ_1 Физический смысл уравнений МаксвеллаСкачать

60. Уравнения МаксвеллаСкачать

1.1. Решение системы уравнений Максвелла методом интегральных преобразованийСкачать

3 14 Уравнения МаксвеллаСкачать

Лекция №14 "Электричество и магнетизм" (Попов П.В.): Уравнения МаксвеллаСкачать

Лекция №9. Уравнения МаксвеллаСкачать

Урок 213. Электрические заряды и их взаимодействие. Закон КулонаСкачать

Поляков П. А. - Электромагнетизм - Полная система уравнений Максвелла как результат обобщения опытовСкачать

Вся электростатика для ЕГЭ по физике за 3 часаСкачать

7. Ограниченность уравнений Максвелла. Уточнения уравнений электродинамики. Ацюковский В.А.Скачать