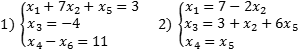Система уравнения определенная или неопределенная (7 видео)

Системы линейных уравнений: основные понятия

— это объединение из n линейных уравнений, каждое из которых содержит k переменных. Записывается это так:

Многие, впервые сталкиваясь с высшей алгеброй, ошибочно полагают, что число уравнений обязательно должно совпадать с числом переменных. В школьной алгебре так обычно и бывает, однако для высшей алгебры это, вообще говоря, неверно.

— это последовательность чисел ( k ₁, k ₂, . k_n ), которая является решением каждого уравнения системы, т.е. при подстановке в это уравнение вместо переменных x ₁, x ₂, . x_n дает верное числовое равенство.

Соответственно, решить систему уравнений — значит найти множество всех ее решений или доказать, что это множество пусто. Поскольку число уравнений и число неизвестных может не совпадать, возможны три случая:

Система несовместна, т.е. множество всех решений пусто. Достаточно редкий случай, который легко обнаруживается независимо от того, каким методом решать систему.
Система совместна и определена, т.е. имеет ровно одно решение. Классический вариант, хорошо известный еще со школьной скамьи.
Система совместна и не определена, т.е. имеет бесконечно много решений. Это самый жесткий вариант. Недостаточно указать, что «система имеет бесконечное множество решений» — надо описать, как устроено это множество.

Переменная x_i называется , если она входит только в одно уравнение системы, причем с коэффициентом 1. Другими словами, в остальных уравнениях коэффициент при переменной x_i должен быть равен нулю.

Если в каждом уравнении выбрать по одной разрешенной переменной, получим набор разрешенных переменных для всей системы уравнений. Сама система, записанная в таком виде, тоже будет называться разрешенной. Вообще говоря, одну и ту же исходную систему можно свести к разным разрешенным, однако сейчас нас это не волнует. Вот примеры разрешенных систем:

Обе системы являются разрешенными относительно переменных x ₁, x ₃ и x ₄. Впрочем, с тем же успехом можно утверждать, что вторая система — разрешенная относительно x ₁, x ₃ и x ₅. Достаточно переписать самое последнее уравнение в виде x ₅ = x ₄.

Теперь рассмотрим более общий случай. Пусть всего у нас k переменных, из которых r являются разрешенными. Тогда возможны два случая:

Число разрешенных переменных r равно общему числу переменных k : r = k . Получаем систему из k уравнений, в которых r = k разрешенных переменных. Такая система является совместной и определенной, т.к. x ₁ = b ₁, x ₂ = b ₂, . x_k = b_k ;
Число разрешенных переменных r меньше общего числа переменных k : r k . Остальные ( k − r ) переменных называются свободными — они могут принимать любые значения, из которых легко вычисляются разрешенные переменные.

Так, в приведенных выше системах переменные x ₂, x ₅, x ₆ (для первой системы) и x ₂, x ₅ (для второй) являются свободными. Случай, когда есть свободные переменные, лучше сформулировать в виде теоремы:

Обратите внимание: это очень важный момент! В зависимости от того, как вы запишете итоговую систему, одна и та же переменная может быть как разрешенной, так и свободной. Большинство репетиторов по высшей математике рекомендуют выписывать переменные в лексикографическом порядке, т.е. по возрастанию индекса. Однако вы совершенно не обязаны следовать этому совету.

Теорема. Если в системе из n уравнений переменные x ₁, x ₂, . x_r — разрешенные, а x _{r + 1}, x _{r + 2}, . x _k — свободные, то:

Если задать значения свободным переменным ( x _{r + 1} = t _{r + 1}, x _{r + 2} = t _{r + 2}, . x_k = t_k ), а затем найти значения x ₁, x ₂, . x_r , получим одно из решений.
Если в двух решениях значения свободных переменных совпадают, то значения разрешенных переменных тоже совпадают, т.е. решения равны.

В чем смысл этой теоремы? Чтобы получить все решения разрешенной системы уравнений, достаточно выделить свободные переменные. Затем, присваивая свободным переменным разные значения, будем получать готовые решения. Вот и все — таким образом можно получить все решения системы. Других решений не существует.

Вывод: разрешенная система уравнений всегда совместна. Если число уравнений в разрешенной системе равно числу переменных, система будет определенной, если меньше — неопределенной.

И все бы хорошо, но возникает вопрос: как из исходной системы уравнений получить разрешенную? Для этого существует метод Гаусса.

Содержание

Системы линейных уравнений
Классификация систем линейных уравнений
Исследование СЛАУ. Общие сведения
Общие сведения (определения, условия, методы, виды)
Ранг матрицы и его свойства
🌟 Видео

Видео:Совместные и несовместные, определенные и неопределенные системы линейных уравненийСкачать

Системы линейных уравнений

Видео:Определенные и неопределенные системы уравненийСкачать

Классификация систем линейных уравнений

Определение. Две системы называются эквивалентными, если решение первой является решением второй и наоборот.

Определение. Система, имеющая хотя бы одно решение, называется совместной. Система, не имеющая ни одного решения, называется несовместной.

Определение. Система, имеющая единственное решение, называется определенной, а имеющая более одного решения – неопределенной.

Видео:Математика без Ху!ни. Метод Гаусса. Совместность системы. Ранг матрицы.Скачать

Исследование СЛАУ. Общие сведения

В данной статье мы расскажем о методах, видах, условиях и определениях исследований решений систем линейных уравнений, что такое метод Кронекера-Капели, а также приведем примеры.

Видео:Решение системы уравнений методом ГауссаСкачать

Общие сведения (определения, условия, методы, виды)

Системы линейных алгебраических уравнений с n неизвестными могут иметь:

единственное решение;
бесконечное множество решение (неопределенные СЛАУ);
ни одного решения (несовместные СЛАУ).

Пример 1

Система x + y + z = 1 2 x + 2 y + 2 z = 3 не имеет решений, поэтому она несовместна.

Система x + y = 1 2 x + 7 y = — 3 имеет единственное решение x = 2 ; y = 1 .

Система x + y = 1 2 x + 2 y = 2 3 x + 3 y = 3 имеет бесконечное множество решений x = t y = 1 — t при — ∞ t ∞ .

Перед решением системы уравнений необходимо исследовать систему, т.е. ответить на следующие вопросы:

Совместна ли система?
Если система совместна, то, какое количество решений она имеет — одно или несколько?
Как найти все решения?

Если система малоразмерна при m = n , то ответить на поставленные вопросы можно при помощи метода Крамера:

если основной определитель системы, то система совместна и имеет единственное решение, которое вычисляется методом Крамера;
если, и один из вспомогательных определителей, то система не является совместной, т.е. не имеет решений;
если и все, и один из коэффициентов СЛАУ, то система не является определенной и имеет бесконечное множество решений.

Видео:Математика без Ху!ни. Метод Гаусса.Скачать

Ранг матрицы и его свойства

Бывают случаи, которые выбиваются из представленных вариантов решения СЛАУ, например, линейные уравнения с большим количеством уравнений и неизвестных.

Для такого варианта решения существует ранг матрицы, который представляет собой алгоритм действий в случае решения системы матрицы, когда

В математике выделяют следующие подходы к определению ранга матрицы:

при помощи понятия линейной зависимости/независимости строк/столбцов матрицы. Ранг равен максимальному количеству независимых строк (столбцов) матрицы
при помощи понятия минора матрицы в качестве наивысшего порядка минора, который отличается от нуля. Минор матрицы порядка k — определитель k-го порядка, составленный из элементов, которые стоят на пересечении вычеркиваемых k-строк и k-столбцов матрицы;
при помощи метода Гаусса. По завершении прямого хода ранг матрицы равняется количеству ненулевых строк.

Обозначение ранга матрицы: r ( A ) , r g ( A ) , r A .

Свойства ранга матрицы:

квадратная невырожденная матрица обладает рангом, который отличается от нуля;
если транспонировать матрицу, то ранг матрицы не изменяется;
если поменять местами 2 параллельные строки или 2 параллельных столбца, ранг матрицы не изменяется;
при удалении нулевого столбца или строки ранг матрицы не изменяется;
ранг матрицы не изменяется, если удалить строку или столбец, которые являются линейной комбинацией других строк;
при умножении все элементов строки/столбца на число k н е р а в н о н у л ю ранг матрицы не изменяется;
ранг матрицы не больше меньшего из ее размеров: r ( А ) ≤ m i n ( m ; n ) ;
когда все элементы матрицы равны нулю, то только тогда r ( A ) = 0 .

Пример 2

А 1 = 1 1 1 2 2 2 3 3 3 , B 1 = 1 0 0 0 0 0

r ( A 1 ) = 1 , r ( B 1 ) = 1

А 2 = 1 2 3 4 0 5 6 7 0 0 0 0 ; В 2 = 1 1 3 1 2 1 4 3 1 2 5 0 5 4 13 6