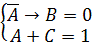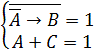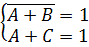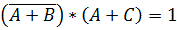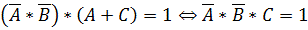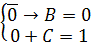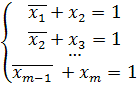Система уравнений в алгебре логики

Можно выделить различные способы решения систем логических уравнений. Это сведение к одному уравнению, построение таблицы истинности и декомпозиция.

Задача: Решить систему логических уравнений:

Рассмотрим метод сведения к одному уравнению. Данный метод предполагает преобразование логических уравнений, таким образом, чтобы правые их части были равны истинностному значению (то есть 1). Для этого применяют операцию логического отрицания. Затем, если в уравнениях есть сложные логические операции, заменяем их базовыми: «И», «ИЛИ», «НЕ». Следующим шагом объединяем уравнения в одно, равносильное системе, с помощью логической операции «И». После этого, следует сделать преобразования полученного уравнения на основе законов алгебры логики и получить конкретное решение системы.

Решение 1: Применяем инверсию к обеим частям первого уравнения:

Представим импликацию через базовые операции «ИЛИ», «НЕ»:

Поскольку левые части уравнений равны 1, можно объединить их с помощью операции “И” в одно уравнение, равносильное исходной системе:

Раскрываем первую скобку по закону де Моргана и преобразовываем полученный результат:

Полученное уравнение, имеет одно решение: A =0, B=0 и C=1.

Следующий способ – построение таблиц истинности. Поскольку логические величины имеют только два значения, можно просто перебрать все варианты и найти среди них те, при которых выполняется данная система уравнений. То есть, мы строим одну общую таблицу истинности для всех уравнений системы и находим строку с нужными значениями.

Решение 2: Составим таблицу истинности для системы:

Полужирным выделена строчка, для которой выполняются условия задачи. Таким образом, A=0, B=0 и C=1.

Способ декомпозиции. Идея состоит в том, чтобы зафиксировать значение одной из переменных (положить ее равной 0 или 1) и за счет этого упростить уравнения. Затем можно зафиксировать значение второй переменной и т.д.

Решение 3: Пусть A = 0, тогда:

Из первого уравнения получаем B =0, а из второго – С=1. Решение системы: A = 0, B = 0 и C = 1.

В ЕГЭ по информатике очень часто требуется определить количество решений системы логических уравнений, без нахождения самих решений, для этого тоже существуют определенные методы. Основной способ нахождения количества решений системы логических уравнений – замена переменных . Сначала необходимо максимально упростить каждое из уравнений на основе законов алгебры логики, а затем заменить сложные части уравнений новыми переменными и определить количество решений новой системы. Далее вернуться к замене и определить для нее количество решений.

Задача: Сколько решений имеет уравнение ( A → B ) + ( C → D ) = 1? Где A, B, C, D – логические переменные.

Решение: Введем новые переменные: X = A → B и Y = C → D . С учетом новых переменных уравнение запишется в виде: X + Y = 1.

Дизъюнкция верна в трех случаях: (0;1), (1;0) и (1;1), при этом X и Y является импликацией, то есть является истинной в трех случаях и ложной – в одном. Поэтому случай (0;1) будет соответствовать трем возможным сочетаниям параметров. Случай (1;1) – будет соответствовать девяти возможным сочетаниям параметров исходного уравнения. Значит, всего возможных решений данного уравнения 3+9=15.

Следующий способ определения количества решений системы логических уравнений – бинарное дерево. Рассмотрим данный метод на примере.

Задача: Сколько различных решений имеет система логических уравнений:

Приведенная система уравнений равносильна уравнению:

Предположим, что x ₁ – истинно, тогда из первого уравнения получаем, что x ₂ также истинно, из второго — x ₃=1, и так далее до x_m = 1. Значит набор (1; 1; …; 1) из m единиц является решением системы. Пусть теперь x ₁=0, тогда из первого уравнения имеем x ₂ =0 или x ₂ =1.

Когда x ₂ истинно получаем, что остальные переменные также истинны, то есть набор (0; 1; …; 1) является решением системы. При x ₂=0 получаем, что x ₃=0 или x ₃=, и так далее. Продолжая до последней переменной, получаем, что решениями уравнения являются следующие наборы переменных ( m +1 решение, в каждом решении по m значений переменных):

Такой подход хорошо иллюстрируется с помощью построения бинарного дерева. Количество возможных решений – количество различных ветвей построенного дерева. Легко заметить, что оно равно m +1.

Видео:Системы логических уравнений содержащие НЕОДНОТИПНЫЕ УРАВНЕНИЯ [Алгебра логики] #8Скачать

Решение систем логических уравнений — Основы логики

В алгебре логики изучаются логические операции, производимые над высказываниями. Такие высказывания могут быть истинными или ложными. Применяя к простым высказываниям логические операции, можно строить составные высказывания.

Основные логические операции

• Отрицание (инверсия, логическое НЕ)

Смысл операции: результат меняется на противоположный (вместо истины — ложь, вместо лжи — истина).

• Логическое сложение (дизъюнкция, логическое ИЛИ)

Смысл операции: результат — истина, если хотя бы один операнд — истина (операндом называется то значение или та переменная, над которым (которой) осуществляется операция).

Обозначения: V или +.

• Логическое умножение (конъюнкция, логическое И)

Смысл операции: результат — истина, если оба операнда — истина.

Обозначения: Λ или &.

• Исключающее ИЛИ (сложение по модулю 2, строгая дизъюнкция)

Смысл операции: результат — истина, если операнды различны.

Смысл операции: из лжи может следовать что угодно, а из истины — только истина.

Смысл операции: результат — истина, если операнды одинаковы.

Если в логическом выражении используется несколько логических операций, то их порядок определяется приоритетами логических операций:

Операцию “импликация” можно выразить через “ИЛИ” и “НЕ”:

Операцию “эквиваленция” также можно выразить через “ИЛИ” и “НЕ”:

Поразрядные (побитовые) логические операции

Кроме обычных логических операций, применимых по отношению к логическим переменным, возможны поразрядные (побитовые) логические операции, выполняемые для пар “одноименных” (соответствующих одним и тем же разрядам) битов двух целых чисел. При этом двоичное значение 1 рассматривается как “истина”, а значение 0 — как “ложь”. Результатом выполнения поразрядной логической операции является целое число.

Для каждой пары битов выполняется логическая операция “И”.

Для каждой пары битов выполняется логическая операция “ИЛИ”.

Основные законы алгебры логики

Закон непротиворечия (высказывание не может быть одновременно истинным и ложным)

Закон исключения третьего (либо высказывание, либо его отрицание должно быть истинным)

Закон двойного отрицания

Законы де Моргана

Законы рефлексивности (идемпотенции)

Свойства логических констант 1 и 0

Полезно запомнить следующее правило: если известно количество решений уравнения F(x₁, х₂, . х_n) = 1, то количество возможных решений “противоположного” уравнения F(x₁, х₂, . х_n) = 0 равно разности количества всех возможных комбинаций значений переменных х₁, х₂. х_n (которое равно 2 n ) и количества решений уравнения F(x₁, х₂, . х_n) = 1 (и, соответственно, наоборот):

Это правило легко доказать, рассмотрев полную таблицу истинности логической функции F(x₁, х₂, . х_n): если исключить из нее строки, соответствующие значению F = 1, то останутся строки, соответствующие значению F = 0,и наоборот.

Разбор типовых задач

Задача 1. Сколько различных решений имеет система уравнений

В ответе не нужно перечислять все различные наборы значений х₁, х₂, . х₁₀, при которых выполнена данная система равенств. В качестве ответа вам нужно указать количество таких наборов.

1) Анализируется первое уравнение:

Последняя выполняемая операция здесь — И, поэтому:

Следует обратить внимание: в обеих частях записаны одни и те же тождества, только в первом случае они записаны “как есть”, а во втором — с отрицаниями. Тогда, если (х₁ ≡ х₂) = 1 и (х₃ ≡ х₄) = 1, то первая запись будет истинной, но тогда ¬(x₁ ≡ х₂) и ¬(х₃ ≡ х₄) оба будут ложными, и вторая запись ложна. И наоборот, при (х₁ ≡ х₂) = 0 и (х₃ ≡ х₄) = 0 первая запись будет ложной, а вторая (с отрицаниями) — истинной. Не подходит ни тот, ни другой вариант. “Спасает положение” то, что тождества в обеих записях соединены операцией ИЛИ, т.е. оба раза достаточно, чтобы единице было равно хотя бы одно из этих тождеств.

Вывод: чтобы первое уравнение системы было равно 1, нужно, чтобы либо (х₁ ≡ х₂) = 1 и (х₃ ≡ х₄) = 0, либо, наоборот, (х₁ ≡ х₂) = 0 и (х₃ ≡ х₄) = 1.

Первое из этих “либо” даёт такие варианты значений переменных, когда х₁ и х₂ одинаковы, а х₃ и х₄ различны:

Второе “либо”, аналогично, даёт варианты, в которых, наоборот, х₁ и х₂ различны, а х₃ и х₄ одинаковы:

Всего — 8 вариантов.

2) Добавляется в анализ второе уравнение:

Рассуждая аналогично и учитывая, что для х₃ и х₄ возможные варианты “унаследованы” от предыдущего уравнения, получается, что в вариантах значений х₅, х₆, добавленных этим вторым уравнением, для одинаковых значений х₃ и х₄ должны быть разными значения х₅ и х₆, а для различных значений х₃ и х₄ — одинаковые значения х₅ и х₆:

Итого из 8 предыдущих вариантов благодаря второму уравнению получается 16 (вдвое больше).

3) Очевидно, такая тенденция сохранится и дальше, ведь уравнения системы — типовые. Значит, добавление в рассмотрение третьего уравнения, пропущенного в записи системы и использующего переменные х₅, х₆, х₇, x₈, снова удвоит количество вариантов значений переменных: из 16 их получится 32.

Аналогично, последнее, четвёртое уравнение системы (переменные х₇, х₈, х₉, х₁₀) снова удваивает количество вариантов, “унаследованное” от предыдущего уравнения. В итоге для всей системы уравнений получается 64 возможных варианта значений переменных x₁ — x₁₀.

Ответ: 64 варианта значений переменных.

Задача 2. Сколько существует различных наборов значений логических переменных x₁, х₂, х₃, х₄, х₅, у₁, у₂, у₃, у₄, у₅, которые удовлетворяют всем перечисленным ниже условиям?

В ответе не нужно перечислять все различные наборы значений переменных x₁, х₂, х₃, х₄, х₅, y₁, у₂, у₃, у₄, у₅, при которых выполнена данная система равенств. В качестве ответа вам нужно указать количество таких наборов.

Как и всегда при решении задач с системами логических уравнений, нужно сначала проанализировать каждое уравнение в отдельности. При этом, первое и второе уравнения заданной системы практически идентичны (с точностью до имён переменных — “игреки” вместо “иксов”), и это существенно облегчает работу.

Анализируя первое уравнение:

Таблица истинности логической операции следования: единственная ситуация, при которой её результат равен нулю, — когда из единицы следует нуль, а во всех других случаях эта операция возвращает единицу:

Кроме того, поскольку все отдельные операции следования в первом уравнении соединены операцией И, для выполнения заданного в нём равенства требуется, чтобы все операции следования давали в результате единицу.

Чтобы найти все возможные комбинации значений переменных, задействованных в первом уравнении, удобнее всего выполнить построение дерева решений: это позволит не запутаться и не пропустить какие-то варианты. При построении дерева на каждом его очередном шаге анализируется очередная пара переменных и для каждой имеющейся ветви определяются дальнейшие варианты ветвления. Слева указываются логические операции следования, которые и анализируются на соответствующих шагах (уровнях дерева). Ключевым моментом при построении дерева является уже отмеченный выше факт, что для получения единичного результата из нуля может следовать любое значение второй переменной, а из единицы — только единица.

Основную идею при построении данного дерева можно условно выразить фразой: “размножаются только нули”. То есть если имеется начало набора значений пяти переменных, которое на данный момент завершается нулём, то продолжить его можно как нулём, так и единицей (в дереве имеется ветвление), но если текущая последовательность заканчивается единицей, то продолжать её можно только единицей, и в дереве не будет никакого ветвления, а только продолжение уже существующей ветви.

Полный набор возможных значений переменных, удовлетворяющих первому уравнению, тогда содержится в самой нижней строке построенного дерева (в его “листьях”): (х₁х₂х₃х₄х₅) = (00000), (00001), (00011), (00111), (01111), (11111).

Второе уравнение по структуре полностью совпадает с первым. Поэтому анализировать его нет необходимости, и можно сразу записать набор возможных для него значений переменных: (y₁y₂y₃y₄y₅) = (00000), (00001), (00011), (00111), (01111), (11111).

Если бы в условии задачи присутствовали только рассмотренные два уравнения, то, поскольку в них нет общих переменных, решением этой системы уравнений были бы все возможные попарные сочетания найденных наборов значений “иксов” и “игреков”. Именно третье уравнение, в котором одной логической операцией связаны один из “иксов” и один из “игреков”, является “ключом”, определяющим выбор: какие из найденных комбинаций наборов значений (х₁х₂х₃х₄х₅) и (y₁y₂y₃y₄y₅) подходят, а какие — нет.

Запись этого третьего уравнения:

Согласно ему, из всех найденных пар наборов значений “иксов” и “игреков” для решения подходят только такие, в которых значения указанных переменных соответствуют истинности заданной логической операции, т.е.:

• когда в наборе значений (y₁y₂y₃y₄y₅) пятая цифра равна нулю, в пару с ним годятся любые наборы значений (х₁х₂х₃х₄х₅), поскольку, что бы в них ни стояло в пятой позиции (0 или 1), результат операции у₅→ х₅ = 1 в любом случае будет равен 1 (см. таблицу истинности для этой операции);

• когда в наборе значений (y₁y₂y₃y₄y₅) пятая цифра равна единице, в пару с ним годятся только такие наборы значений (х₁х₂х₃х₄х₅), в которых пятая цифра равна 1.

Удобнее и нагляднее всего расписать все получаемые комбинации значений х и y виде таблицы (“матрицы решений”). Анализируемые цифры в ней выделены подчеркиванием.

Видео:Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

Решение систем логических уравнений

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Описание презентации по отдельным слайдам:

14.06.2005 (формальная) Математическая логика Часть 5. Решение систем логических уравнений

Системы логических уравнений (ЕГЭ-2011) Три типа задач: I тип — В уравнениях используется операции дизъюнкции (конъюнкции), одна переменная входит в 2 уравнения. II тип — В уравнениях используется операции дизъюнкции (конъюнкции), сложные переменные представлены тождеством, одна сложная переменная входит в 2 уравнения. III тип — В уравнениях используется операции дизъюнкции (конъюнкции), сложные переменные, которые могут быть упрощены путем введения независимых новых переменных и применения законов логических преобразований. IV тип — В уравнениях используется операции дизъюнкции (конъюнкции), сложные переменные, которые не могут быть упрощены путем введения независимых новых переменных. V тип – Одна переменная входит в одно слагаемое во всех уравнениях VI, VII тип – Одна переменная входит во все слагаемые в уравнении одним из наиболее известных проектов создания компьютеров пятого поколения пред­полагается использование логических исчислений в качестве ос­новной системы программирования. Поэтому специалисты, ра­ботающие в различных областях информатики, проявляют все большее внимание и интерес к математической логике. Проник­новение методов математической логики в информатику уже привело к новым результатам, имеющим первостепенное практичес­кое значение. В частности, к созданию нового языка программи­рования ПРОЛОГ — языка, принципиально отличающегося от всех созданных ранее.

I тип Сколько различных решений имеет система уравнений ¬X1  X2 = 1 ¬X2  X3 = 1 . ¬X9  X10 = 1 где x1, x2, …, x10 – логические переменные? В ответе не нужно перечислять все различные наборы значений переменных, при которых выполнено данное равенство. В качестве ответа нужно указать количество таких наборов. ¬X1  X2 = 1 Ответ: 11 вариантов решений Типы уравнений I Решаем второе уравнение http://krolyakov.narod.ru ¬X1 = 0 X2 = 1 ¬X1 = 1 X2 = 0 ¬X1 = 1 X2 = 1 X1 = 1 X2 = 1 X1 = 0 X2 = 0 X1 = 0 X2 = 1 X2 = 1 X3 = 1 X2 = 0 X3 = 0 X2 = 0 X3 = 1 X2 X1 0 0 1 0 1 1 X3 X2 X1 0 0 0 1 0 0 1 1 0 1 1 1 Кол-во уравнений Кол-вопеременных Кол-во вариантов решений 1 2 3 2 3 4 3 4 5 Решаем по очереди уравнения и ищем закономерности накопления вариантов решений:

Сколько различных решений имеет система уравнений X1  ¬ X2 = 1 X2  ¬ X3 = 1 . X9  ¬ X10 = 1 где x1, x2, …, x10 – логические переменные? Решаем самостоятельно Первое уравнение: X1  ¬ X2 = 1 Второе уравнение: X2  ¬ X3 = 1 Ответ: 11 вариантов решений http://krolyakov.narod.ru X1 = 0 ¬ X2 = 1 X1 = 1 ¬ X2 = 0 X1 = 1 ¬ X2 = 1 X1 = 0 X2 = 0 X1 = 1 X2 = 1 X1 = 1 X2 = 0 X2 = 0 X3 = 0 X2 = 1 X3 = 1 X2 = 1 X3 = 0 X2 X1 0 0 0 1 1 1 X3 X2 X1 0 0 0 0 0 1 0 1 1 1 1 1 Кол-вопеременных Кол-во вариантов решений 2 3 3 4 4 5

Сколько различных решений имеет система уравнений ¬X1  X2 = 0 ¬X2  X3 = 0 . ¬X9  X10 = 0 где x1, x2, …, x10 – логические переменные? Сколько различных решений имеет система уравнений ¬X1  X2 = 0 ¬X2  X3 = 0 . ¬X9  X10 = 0 где x1, x2, …, x10 – логические переменные? Сколько различных решений имеет система уравнений ¬X1  X2 = 1 ¬X2  X3 = 1 . ¬X9  X10 = 1 где x1, x2, …, x10 – логические переменные? Нет решения I 11 вариантов Нет решения Решаем по очереди уравнения и ищем закономерности накопления вариантов решений:

Вывод: Система уравнений типа ¬X1  X2 = 1, где используются операции дизъюнкции и одна переменная входит в 2 уравнения, имеют решение только в случае, когда дизъюнкция двух переменных равна 1. Кол-во вариантов решений = кол-во уравнений + 2, или Кол-во вариантов решений = кол-во переменных + 1. I

Задача 1. Следующие два высказывания истинны: Неверно, что если корабль А вышел в море, то корабль С – нет. В море вышел корабль В или корабль С, но не оба вместе. Какие корабли вышли в море. А= «корабль А вышел в море» В= «корабль В вышел в море» С= «корабль С вышел в море» А→ ¬ С = 0 А  В = 1 Последовательное решение уравнений: А  В = 1 А = 1 В = 0 А = 0 В = 1 А→ ¬ С = 0 А = 1 ¬ С = 0 А = 1 С = 1 А = 1 В = 0 С=1 Ответ:

II тип Сколько различных решений имеет система уравнений ¬(X1  X2)  (X3  X4) = 1 ¬(X3  X4)  (X5  X6) = 1 ¬(X5  X6)  (X7  X8) = 1 ¬(X7  X8)  (X9  X10) = 1 где x1, x2, …, x10 – логические переменные? В ответе не нужно перечислять все различные наборы значений переменных, при которых выполнено данное равенство. В качестве ответа нужно указать количество таких наборов. Введем обозначение сложных переменных: Y1 = (X1  X2) Y2= (X3  X4) Y3 = (X5  X6) Y4 = (X7  X8) Y5 = (X9  X10) Запишем систему уравнений: ¬Y1  Y2 = 1 ¬Y2  Y3 = 1 ¬Y3  Y4 = 1 ¬Y4  Y5 = 1 Cистема имеет 6 вариантов решений. Переменные Y — независимые II http://krolyakov.narod.ru Y5 Y4 Y3 Y2 Y1 0 0 0 0 0 1 0 0 0 0 1 1 0 0 0 1 1 1 0 0 1 1 1 1 0 1 1 1 1 1

Найдем варианты решений для исходных переменных Кол-во комбинаций для одного варианта решений: N=25=32 Всего решений: 32*6=192 Алгоритм 1. Ввести обозначения для сложных переменных. 2. Записать систему для новых переменных. 3. Найти количество вариантов решений для системы с новыми переменными (m). 4. Определить число состояний (k) исходных переменных для одного варианта решения. 5. Определить число комбинаций (N) с учетом всего количества введенных переменных (n): N=kn 6. Определить итоговое количество вариантов решения системы: N*m II http://krolyakov.narod.ru Y1 = 0; Y1 = 1; X1 =1; X2=0; X1 =0; X2=1; X1 =0; X2=0; X1 =1; X2=1; X1  X2=0; X1  X2=1;

III. Сколько различных решений имеет система уравнений (X1  X2)  (¬X1  ¬X2)  (¬X3  X4)  (X3  ¬X4) = 1 (X3  X4)  (¬X3  ¬X4)  (¬X5  X6)  (X5  ¬X6) = 1 (X5  X6)  (¬X5  ¬X6)  (¬X7  X8)  (X7  ¬X8) = 1 (X7  X8)  (¬X7  ¬X8)  (¬X9  X10)  (X9  ¬X10) = 1 где x1, x2, …, x10 – логические переменные? Используется закон замены эквивалентности: A  B = (A  B)  (¬ A  ¬B) и замены инверсии эквивалентности: ¬ (A  B) = ¬((A  B)  (¬ A  ¬B)) = ¬(A  B)  ¬(¬ A  ¬B) = (¬ A ¬ B)  (A  B) = ¬ A  A  ¬ A  B  A ¬ B  ¬ B  B = (¬ A  B)  (A ¬ B ) III (X1  X2)  ¬ (X3  X4) =1 (X3  X4)  ¬ (X5  X6) =1 (X5  X6)  ¬ (X7  X8) =1 (X7  X8)  ¬ (X9  X10) =1 Упростим уравнения: Решить самостоятельно. Проверка http://krolyakov.narod.ru

Замена эквивалентности Закон замены эквивалентности: A  B = (A  B)  (¬ A  ¬B) Замена инверсии эквивалентности: ¬ (A  B) = ¬((A  B)  (¬ A  ¬B)) = ¬(A  B)  ¬(¬ A  ¬B) = (¬ A ¬ B)  (A  B) = ¬ A  A  ¬ A  B  A ¬ B  ¬ B  B = (¬ A  B)  (A ¬ B )

Введем обозначение сложных переменных: Y1 = (X1  X2) Y2= (X3  X4) Y3 = (X5  X6) Y4 = (X7  X8) Y5 = (X9  X10) Запишем систему уравнений: Y1  ¬Y2 = 1 Y2  ¬Y3 = 1 Y3  ¬Y4 = 1 Y4  ¬Y5 = 1 Cистема имеет 6 вариантов решений. III Найдем варианты решений для исходных переменных N=25=32 Всего решений: 32*6=192 http://krolyakov.narod.ru Y1 = 0; Y1 = 1; X1  X2=0; X1  X2=1; X1 =1; X2=0; X1 =0; X2=1; X1 =0; X2=0; X1 =1; X2=1; Y5 Y4 Y3 Y2 Y1 0 0 0 0 0 0 0 0 0 1 0 0 0 1 1 0 0 1 1 1 0 1 1 1 1 1 1 1 1 1

Сколько различных решений имеет система уравнений ((X1  X2)  (X3  X4))  (¬(X1  X2)  ¬(X3  X4)) = 1 ((X3  X4)  (X5  X6))  (¬(X3  X4)  ¬(X5  X6)) = 1 ((X5  X6)  (X7  X8))  (¬(X5  X6)  ¬(X7  X8)) = 1 ((X7  X8)  (X9  X10))  (¬(X7  X8)  ¬(X9  X10)) = 1 где x1, x2, …, x10 – логические переменные? IV Алгоритм решения: Вводим обозначения сложных высказываний и переписываем уравнения. Упрощаем уравнения, используя замену эквивалентности и инверсии эквивалентности. Определяем количество вариантов решения для веденных переменных. Определяем количество комбинаций исходных переменных для одного варианта. Определяем итоговое количество вариантов решения Решаем самостоятельно http://krolyakov.narod.ru

Введем обозначение сложных переменных: Y1 = (X1  X2) Y2= (X3  X4) Y3 = (X5  X6) Y4 = (X7  X8) Y5 = (X9  X10) Запишем систему уравнений: (Y1  Y2)  (¬ Y1  ¬ Y2) = 1 (Y2  Y3)  (¬ Y2  ¬ Y3) = 1 (Y3  Y4)  (¬ Y3  ¬ Y4) = 1 (Y4  Y5)  (¬ Y4  ¬ Y5) = 1 Cистема имеет 2 варианта решения. IV Упростим уравнения: Y1  Y2 = 1 Y2  Y3 = 1 Y3  Y4 = 1 Y4  Y5 = 1 Кол-во комбинаций для одного варианта решений: N=25=32 Всего решений: 32*2=64 http://krolyakov.narod.ru Y5 Y4 Y3 Y2 Y1 0 0 0 0 0 1 1 1 1 1

Сколько различных решений имеет система уравнений (X2  X1)  (X2  X3)  (¬X2 ¬ X3)= 1 (X3  X1)  (X3  X4)  (¬X3 ¬ X4)= 1 . (X9  X1)  (X9  X10)  (¬X9 ¬ X10)= 1 (X10  X1) = 0 где x1, x2, …, x10 – логические переменные? V Используется закон замены эквивалентности: (X2  X1)  (X2  X3) = 1 (X3  X1)  (X3  X4) = 1 . (X9  X1)  (X9  X10)= 1 (X10  X1) = 0 http://krolyakov.narod.ru Применить замену переменных нельзя, так как не получится независимых переменных. Решаем табличным способом по уравнению.

V (X2  X1)  (X2  X3) = 1 Решаем второе уравнение: (X3  X1)  (X3  X4) = 1 Решаем первое уравнение: X2  X1=0 X2  X3=1 X2  X1=1 X2  X3=0 X2  X1=1 X2  X3=1 X1=0 X2 =1 X3=1 X1=1 X2 =0 X3=0 X1=1 X3 =1 X4=0 X1=0 X2 =0 X3=1 X1=1 X2 =1 X3=1 X1=0 X2 =0 X3=0 X3  X1=0 X3  X4=1 X3  X1=1 X3  X4=0 X3  X1=1 X3  X4=1 X1=0 X3 =1 X4=1 X1=1 X3 =0 X4=0 X1=1 X2 =1 X3=0 X1=0 X3 =0 X4=1 X1=1 X3 =1 X4=1 X1=0 X3 =0 X4=0 X1 X3 X2 0 0 0 0 1 0 1 0 0 0 1 1 1 0 1 1 1 1 X1 X4 X3 X2 0 0 0 0 0 1 0 0 0 1 1 0 1 0 0 0 0 1 1 1 1 0 0 1 1 1 1 1 1 0 1 1 Кол-вопере-менных Кол-во вариантов решений 3 6 4 8 5 10 6 12 7 14 8 16 9 18 10 20

V (X10  X1) = 0 X10 X1 Подключаем последнее уравнение: Ответ: Кол-во решений = 20-2=18 http://krolyakov.narod.ru X1 X4 X3 X2 0 0 0 0 0 1 0 0 0 1 1 0 1 0 0 0 0 1 1 1 1 0 0 1 1 1 1 1 1 0 1 1

VI. Сколько различных решений имеет система уравнений (X1  X2)  (¬X1  ¬X2)  (X1  X3) = 1 (X2  X3)  (¬X2  ¬X3)  (X2  X4) = 1 . (X8  X9)  (¬X8  ¬X9)  (X8  X10) = 1 где x1, x2, …, x10 – логические переменные? VI Решаем самостоятельно Применим закон замены эквивалентности: (X1  X2)(X1  X3)=1 (X2  X3)(X2  X4)=1 . (X8  X9)(X8  X10)=1 http://krolyakov.narod.ru Независимые переменные ввести нельзя, решаем по уравнению

Решаем первое уравнение: (X1  X2)(X1  X3)=1 Решаем второе уравнение: (X2  X3)(X2  X4)=1 VI http://krolyakov.narod.ru X1  X2=0 X1  X3=1 X1=0 X2 =1 X3=0 X1=1 X2 =0 X3=1 X1=0 X2 =0 X3=1 X1=1 X2 =1 X3=1 X1=0 X2 =0 X3=0 X1=1 X2 =1 X3=0 X1  X2=1 X1  X3=0 X1  X2=1 X1  X3=1 X2  X3=0 X2  X4=1 X2  X3=1 X2  X4=0 X2  X3=1 X2  X4=1 X2=0 X3 =1 X4=0 X2=1 X3 =0 X4=1 X2=0 X3 =0 X4=1 X2=1 X3 =1 X4=1 X2=0 X3 =0 X4=0 X2=1 X3 =1 X4=0 X3 X2 X1 0 0 0 1 0 0 0 1 0 1 0 1 0 1 1 1 1 1 X4 X3 X2 X1 0 0 0 0 1 0 0 0 1 0 1 0 1 0 1 1 1 1 1 1 X4 X3 X2 X1 0 0 0 0 1 0 0 0 0 1 0 0 1 0 1 0 0 1 0 1 1 0 1 1 0 1 1 1 1 1 1 1

Ответ: 20 вариантов VI http://krolyakov.narod.ru X3 X2 X1 0 0 0 1 0 0 0 1 0 1 0 1 0 1 1 1 1 1 X4 X3 X2 X1 0 0 0 0 1 0 0 0 0 1 0 0 1 0 1 0 0 1 0 1 1 0 1 1 0 1 1 1 1 1 1 1 Кол-вопеременных Кол-во вариантов решений 3 6 4 8 5 10 6 12 7 14 8 16 9 18 10 20 i Xi=Xi-1 XiXi-1 всего решений 3 2 4 6 4 2 2+4=6 8 5 2 2+6=8 10 6 2 2+8=10 12 7 2 2+10=12 14 8 2 2+12=14 16 9 2 2+14=16 18 10 2 2+16=18 20

(X1  X2)(X1  X3)=1 (X2  X3)(X2  X4)=1 . (X8  X9)(X8  X10)=1 Решение при помощи графа: дерево 1 0 X1 X2 1 X3 1 0 0 1 1 0 1 0 0 2 4 6 1 0 X4 1 0 0 1 0 1 8 Ответ: 20 вариантов VI X1=0 X2 =1 X3=0 X1=1 X2 =0 X3=1 X1=0 X2 =0 X3=1 X1=1 X2 =1 X3=1 X1=0 X2 =0 X3=0 X1=1 X2 =1 X3=0 X2=0 X3 =1 X4=0 X2=1 X3 =0 X4=1 X2=0 X3 =0 X4=1 X2=1 X3 =1 X4=1 X2=0 X3 =0 X4=0 X2=1 X3 =1 X4=0

VII Сколько различных решений имеет система уравнений (X1  X2)  (¬X1  ¬X2)  (X2  X3)  (¬X2  ¬X3) = 1 (X2  X3)  (¬X2  ¬X3)  (X3  X4)  (¬X3  ¬X4) = 1 . (X8  X9)  (¬X8  ¬X9)  (X9  X10)  (¬X9  ¬X10) = 1 где x1, x2, …, x10 – логические переменные? Применим закон замены эквивалентности: (X1  X2)(X2  X3)=1 (X2  X3)(X3 X4)=1 . (X8  X9)(X9  X10)=1 Решаем самостоятельно Ответ: 178 вариантов 1 0 X1 X2 1 X3 1 0 0 0 1 0 1 0 1 2 4 6 1 0 X4 0 0 1 1 0 1 10 1 0 0 1 0 0 1 1 0 1 0 1 1 0 1 0 0 1 X5 16

VII i всего решений 3 4 2 6 4 4+2=6 4 10 5 6+4=10 6 16 6 10+6=16 10 26 7 16+10=26 16 42 8 26+16=42 26 68 9 42+26=68 42 110 10 68+42=110 68 178

🎬 Видео

Системы логических уравнений содержащие ОДНОТИПНЫЕ УРАВНЕНИЯ [Алгебра логики] #9Скачать

Математика | Система уравнений на желтую звездочку (feat Золотой Медалист по бегу)Скачать

КАК РЕШАТЬ СИСТЕМЫ ЛОГИЧЕСКИХ УРАВНЕНИЙ. ЕГЭ по информатике. Задание 23Скачать

Решение систем уравнений второго порядка. 8 класс.Скачать

Решить систему логических уравнений. Метод декомпозицииСкачать

Сколько решений имеет лог. уравнение (!(A *B) + C) IMP (!A * !B + D) = 1. Информатика, ЕГЭ, логикаСкачать

Сколько решений имеет логическое уравнение: (A импликация В) ИЛИ (C импликация D). ЕГЭ(информатика)Скачать

9 класс, 11 урок, Методы решения систем уравненийСкачать

Построение таблиц истинностиСкачать

Информатика. Алгебра логики: Таблицы истинности. Центр онлайн-обучения «Фоксфорд»Скачать

Преобразование логических выражений / Упрощение выражений (практика) [Алгебра логики] #6Скачать

Система уравнений VS Система неравенств. ОГЭ по математике №9, 13| Математика TutorOnlineСкачать

Построение таблиц истинностиСкачать

Конъюнкция, дизъюнкция, импликация, эквиваленция, отрицание. На примерах из жизни. Логика.Скачать

Решение систем уравнений методом подстановкиСкачать

Системы логический уравненийСкачать

Система уравнений. Метод алгебраического сложенияСкачать