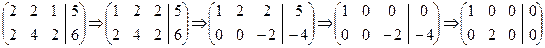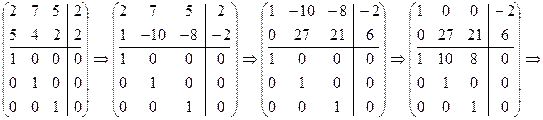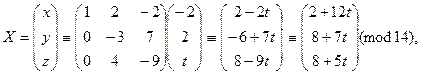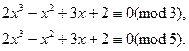Система уравнений сравнения по модулю (7 видео)

Системы линейных сравнений по модулю. Китайская теорема об остатках

Определение 1.Системой m линейных cравнений с n неизвестными x₁, x₂,…, x_n (СЛCУ) называется система cравнений вида:

(1)

Определение 2.Решением системы сравнений (1) называется такой вектор , состоящий из классов вычетов по некоторому модулю m, для которого любой вектор целых чисел

удовлетворяет всем сравнениям системы (1).

Рассмотрим сначала случай, когда все модули m₁,…, m_k в системе (1) равны и система (1) имеет вид:

(2)

Если p простое число, то множество классов вычетов Z_p по модулю p является полем и для системы сравнений применимы все методы решений и основные теоремы, которые имеют место для теории СЛУ над полем.

Пример 1.Решить СЛС

Способ 1. Метод Гаусса:

Все операции выполняются по модулю 7 или в роле Z₇.

Способ 2. Правило Крамера:

Тогда система равносильна системе

Ответ: .

В общем случае для решению системы сравнений вида (2) можно применить методы, изложенные в лекции 2 для решения систем линейных диофантовых уравнений, учитывая следующие замечания:

Нельзя умножать или делить сравнения системы на числа, которые не взаимно простые с модулем, так как при этом может получиться не равносильная система сравнений. Такие преобразования системы назовем элементарными целочисленными приведенными преобразованиями.

Определение 3. Целая матрица D = (d_ij) размерности m´n называется матрицей канонического вида, если она обладает свойствами:

Элементы d_ij, i = 1, 2,…,k, где k = min <m, n>, называем диагональными элементами канонической матрицы. Обозначим число ненулевых диагональных элементов канонической матрицы через r. Очевидно, что r = rang D.

Теорема 1.Любую целую матрицу конечным числом целочисленных приведенных элементарных преобразований строк и столбцов можно привести к матрице канонического вида, при этом r = rang A.

Диагональные элементы d₁₁,…, d_rr, r = rang A, матрицы канонического вида, эквивалентной матрице A, называются элементарными делителями матрицы A.

Теорема 2.Система ЛC (2) разрешима тогда и только тогда, когда НОД(d_ii, m), элементарных делителей d_ii матрицы A делит соответствующие элементарные делители расширенной матрицы СЛС.

Пример 2. Выяснить разрешимость данной СЛС

Решение. Приводим матрицу и расширенную матрицу СЛС к каноническому виду.

Так как элементарные делители матриц равны, то данная СЛДУ разрешима.

Алгоритм решения СЛС Пусть дана СЛС (2). Запишем ее в матричном виде:

Расширенную матрицу СЛДУ (2) расширим вторично, приписав к ней снизу единичную матрицу размерности n´n и нулевую матрицу размерности n´1. Получим дважды расширенную матрицу СЛДУ:

Преобразуем матрицу A к каноническому виду D, выполняя элементарные целочисленные приведенные преобразования над первыми m строками и первыми столбцами n матрицы . Тогда матрица B перейдет в матрицу F = U₁B, где U₁ — произведение элементарных матриц, соответствующих элементарным преобразованиям строк. Единичная матрица E¢ перейдет в матрицу U₂, где U₂ — произведение элементарных матриц, соответствующих элементарным преобразованиям столбцов. Получим матрицу:

Полученной матрице соответствует матричное уравнение:

(5)

Если хотя бы один из элементов f_r _{+ 1} ,…, f_m не сравним с нулем по mod m, или хотя бы одно из чисел f_k не делится на D_k =НОД(d_kk, m), (k =1, 2, …, r), то система (5), а поэтому и система (2) не имеют решений. Если же

Так как Y = U₂ -1 X, то отсюда находим

Пример 3. Решить СЛC:

Решение. Составим дважды расширенную матрицу и приведем ее к каноническому виду:

Отсюда приходим к системе сравнений вида (5):

где t Î Z₁₂. Таким образом, получаем решения сравнения:

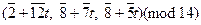
Случай, когда дана СЛУ с различными модулями решается более сложно. Рассмотрим СЛС простейшего вида с одним неизвестным:

(6)

но с различными и попарно взаимно простыми модулями.

Тогда совокупность всех значений x, удовлетворяющих системе (5), определяется сравнением

Доказательство.Для любого j ¹ s все M_j делятся на m_s. Тогда отсюда и из (7) следует, что

Тогда система (6) равносильна системе:

Так как числа m₁,…, m_k – попарно взаимно простые, то система (10) равносильна сравнению (9).ÿ

Из теоремы 3 следует, что для любых попарно взаимно простых целых чисел m₁,…, m_k и любых целых чисел r₁,…, r_k где 0 £ r₁ n + a₁x n — 1 +…+a_n Î Z[x], a₀ T 0(mod p). Рассмотрим сравнение

Так как кольцо классов вычетов Z_p по простому модулю p является полем, то рассматривая сравнение (1) как уравнение над конечным полем Z_p, можем применить к сравнению (1) всю теорию многочленов над конечным полем и получаем следующие теоремы.

Теорема 1.Любое сравнение вида (1) равносильно нулевому сравнению или сравнению степени не большей p-1.

Доказательство.Разделим многочлен f (x) на многочлен x p – x с остатком

где – нулевой многочлен или многочлен степени не выше p-1. Так как по теореме Ферма для любого целого числа a

то сравнение (1) равносильно сравнению

Теорема 2.Число x₀ удовлетворяет сравнению (1) тогда и только тогда, когда

Теорема 3.Если число решений сравнения (1) больше чем n решений, то все его коэффициенты делятся на p.

Доказательство.Допустим, что сравнение (1) имеет, по крайней мере, n + 1 решений. Обозначим числами x₁, x₂, …, x_n₊₁ вычеты этих решений. Деля многочлен f (x) с остатком последовательно на двучлены x — x₁, x — x₂, …, x — x_n представим многочлен f (x) в виде:

Следствие.Если a₀ T 0(mod p), то число решений сравнения (1) не больше степени сравнения.

Доказательство.Допустим, что сравнение (1) имеет более чем n решений, то все его коэффициенты делятся на p. Тогда a₀ º 0(mod p), и получили противоречие с условием.ÿ

Теорема 4(теорема Вильсона).Число p простое, тогда и только тогда, когда справедливо сравнение

Доказательство.Длячисла p = 2 сравнение выполняется. Пусть p – нечетное простое число. Тогда по малой теореме Ферма следует, что сравнение

имеет p -1 решений `0, `1 ,…, `p-1. Тогда по теореме 2 получим:

Отсюда при x º 0(mod p) следует формула (4).ÿ

равносильно системе сравнений

(6)

при этом, число T решений сравнения (5) равно

где T₁,…, T_k – обозначают соответственно число отдельных решений сравнений системы (6).

Доказательство.Первая часть теоремы 1 следует из свойства делимости на взаимно простые числа:число a делится на m тогда и только тогда, когда оно делится на каждый из взаимно простых множителей m₁,…, m_k числа m.

Пусть теперь все попарно различные решения соответственно сравнений системы (6). Тогда для каждого набора чисел ; i=1,…,T₁;…; j=1,…,T_k по формуле (8) предыдущего параграфа находится число, удовлетворяющее всем сравнениям системы (6), т.е. удовлетворяющее системе (5). При этом все полученные числа попарно несравнимы по модулю m. Таким образом система (6) имеет T = T₁… T_k решений.ÿ

Пусть — каноническое разложение числа m. В виду теоремы 5 исследование и решение сравнения

(7)

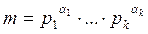
сводится к исследованию и решению сравнений:

. (8)

Поэтому рассмотрим сравнение вида:

, (9)

где p – простое число. Покажем, что решение этого сравнения сводиться к решению сравнения (1).

Теорема 6.Всякое решение x º x₁ (mod p) сравнения (1) при условии, что f´(x₁) не делится на p, даст одно решение сравнения (9):

(10)

Доказательство.Так как всякое число x, удовлетворяющее сравнению (9) удовлетворяет и сравнению (1), то x º x₁ (mod p), где x₁ – какое-нибудь решение сравнения (1).

Обратно, пусть x₁ – любое решение сравнения (1), x º x₁ (mod p). Тогда x = x₁ + pt₁, где t₁ – целое число. Подставляем это значение x в сравнение

(11)

и применяем формулу Тейлора n-го порядка, получим:

Заметим, что в этой формуле все коэффициенты в формуле целые числа и последние n – 2 членов делятся на p. Тогда сравнение (11) принимает вид:

Так как f´(x₁) не делится на p, то последнее сравнение имеет единственное решение

где t₂ – целое число. Тогда выражение для x принимает вид

где t₂ – целое число. Подставляя это значение x в сравнение

(12)

где t₃ – целое число. Тогда выражение для x принимает вид

Продолжая эти рассуждения, получим справедливость утверждения теоремы.ÿ

Пример 1. Решить сравнение

f(x) = 2x 3 — x 2 + 3x +2 º 0 (mod 225). (13)

Так как 225 = 3 2 5 2 , то сравнение равносильно системе сравнений:

(14)

методом испытаний, выполняя проверку по схеме Горнера:

a	-1
-1	mod 3
mod 3
mod 3
-1	mod 5
mod 5
mod 5
mod 5
mod 5

Первое сравнение имеет 1 решение x º 1(mod 3), второе сравнение имеет 1 решение x º 2(mod 5). Далее

f´ (1) = 7 º 1 T 0(mod 3),

f´ (2) = 24 – 4 + 3 = 23 º 3 T 0(mod 5),

то каждое из сравнений (14) и сравнение (13) имеет по одному решению.

Решая первое из сравнений (14) положим x = 1 + 3t₁, где t₁ – целое число. Подставляем это значение x в сравнение, получим

Решая второе из сравнений (14) положим x = 2 + 5t₁, где t₁ – целое число. Подставляем это значение x в сравнение, получим

Все решения сравнения (13) являются решениями системы сравнений:

M₂´ º 9 19 º 9× (9 2 ) 9 º 9×6× (6 2 ) 4 º 4× (11 2 ) 2 º 4× 4 2 º -4×9 º -11 (mod 25),

Тогда число x₀ вычислим о формуле:

Ответ: .

Видео:✓ Сравнение по модулю. Арифметика остатков | Ботай со мной #034 | Борис ТрушинСкачать

Онлайн НОД и НОК, разложение на множители, сравнения по модулю

С помощью данного онлайн-калькулятора можно вычислить НОД и НОК нескольких чисел, разложить число на простые множители, решить линейные и нелинейные сравнения, системы сравнений.

Наибольший общий делитель (НОД, англ. GCD) нескольких целых чисел есть наибольшее из натуральных чисел, которое делит каждое из данных чисел.

Наименьшее общее кратное (НОК, англ. LCM) нескольких целых чисел есть наименьшее из натуральных чисел, которое делится на каждое из данных чисел.

Запишите свои числа через запятую и/или пробел и нажмите кнопку.

Видео:Теория чисел. 6. Методы решения сравнений 1 й степениСкачать

Сравнение чисел по модулю

Определение 1. Если два числа 1 ) a и b при делении на p дают один и тот же остаток r, то такие числа называются равноостаточными или сравнимыми по модулю p.

Утверждение 1. Пусть p какое нибудь положительное число. Тогда всякое число a всегда и притом единственным способом может быть представлено в виде

a=sp+r,

(1)

где s — число, и r одно из чисел 0,1, . p−1.

1 ) В данной статье под словом число будем понимать целое число.

Действительно. Если s получит значение от −∞ до +∞, то числа sp представляют собой совокупность всех чисел, кратных p. Рассмотрим числа между sp и (s+1)p=sp+p. Так как p целое положительное число, то между sp и sp+p находятся числа

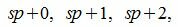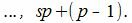Но эти числа можно получить задав r равным 0, 1, 2. p−1. Следовательно sp+r=a получит всевозможные целые значения.

Покажем, что это представление единственно. Предположим, что p можно представить двумя способами a=sp+r и a=s₁p+r₁. Тогда

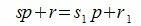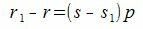(2)

Так как r₁ принимает один из чисел 0,1, . p−1, то абсолютное значение r₁−r меньше p. Но из (2) следует, что r₁−r кратно p. Следовательно r₁=r и s₁=s.

Число r называется вычетом числа a по модулю p (другими словами, число r называется остатком от деления числа a на p).

Утверждение 2. Если два числа a и b сравнимы по модулю p, то a−b делится на p.

Действительно. Если два числа a и b сравнимы по модулю p, то они при делении на p имеют один и тот же остаток p. Тогда

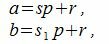где s и s₁ некоторые целые числа.

Разность этих чисел

(3)

делится на p, т.к. правая часть уравнения (3) делится на p.

Утверждение 3. Если разность двух чисел делится на p, то эти числа сравнимы по модулю p.

Доказательство. Обозначим через r и r₁ остатки от деления a и b на p. Тогда

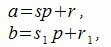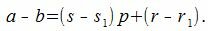По утверждению a−b делится на p. Следовательно r−r₁ тоже делится на p. Но т.к. r и r₁ числа 0,1. p−1, то абсолютное значение |r−r₁| Свойство 1. Для любого a и p всегда

a≡a mod (p).

Свойство 2. Если два числа a и c сравнимы с числом b по модулю p , то a и c сравнимы между собой по тому же модулю, т.е. если

a≡b mod (p), b≡c mod (p).

a≡c mod (p).

Действительно. Из условия свойства 2 следует a−b и b−c делятся на p. Тогда их сумма a−b+(b−c)=a−c также делится на p.

a≡b mod (p) и m≡n mod (p),

a+m≡b+n mod (p) и a−m≡b−n mod (p).

Действительно. Так как a−b и m−n делятся на p, то

(a−b)+ (m−n)=(a+m)−(b+n) ,

(a−b)−(m−n)=(a−m)−(b−n)

также делятся на p.

Это свойство можно распространить на какое угодно число сравнений, имеющих один и тот же модуль.

a≡b mod (p) и m≡n mod (p),

am≡bn mod (p).

Действительно.Так как a−b делится на p, то (a−b)m также делится на p, следовательно

am≡bm mod (p).

Далее m−n делится на p, следовательно b(m−n)=bm−bn также делится на p, значит

bm≡bn mod (p).

Таким образом два числа am и bn сравнимы по модулю с одним и тем же числом bm, следовательно они сравнимы между собой (свойство 2).

a≡b mod (p).

a k ≡b k mod (p).

где k некоторое неотрицательное целое число.

Действительно. Имеем a≡b mod (p). Из свойства 4 следует

a·a≡b·b mod (p).

a·a·a≡b·b·b mod (p).

a k ≡b k mod (p).

Все свойства 1-5 представить в следующем утверждении:

Утверждение 4. Пусть f(x₁, x₂, x₃, . ) целая рациональная функция с целыми коэффициентами и пусть

a₁≡b₁, a₂≡b₂, a₃≡b₃, . mod (p).

f(a₁, a₂, a₃, . )≡f(b₁, b₂, b₃, . ) mod (p).

При делении все обстоит иначе. Из сравнения

am≡bm mod (p)

не всегда следует сравнение

a≡b mod (p).

Утверждение 5. Пусть

am≡bm mod (p),

a≡b mod (p/λ),

Доказательство. Пусть λ наибольший общий делитель чисел m и p. Тогда

m=m₁λ и k=k₁λ.

Так как m(a−b) делится на k, то

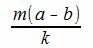имеет нулевой остаток. Тогда

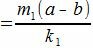имеет нулевой остаток, т.е. m₁(a−b) делится на k₁. Но числа m₁ и k₁ числа взаимно простые. Следовательно a−b делится на k₁=k/λ и, тогда, a≡b mod (p/λ).

Утверждение 6. Если

a≡b mod (p)

и m является один из делителей числа p, то

a≡b mod (m).

Действительно. a−b делится на p. p делится на m. Следовательно a−b делится на m.

Утверждение 7. Если

a≡b mod (p), a≡b mod (q), a≡b mod (s)

a≡b mod (h),

где h наименьшее общее кратное чисел p,q,s.

Действительно. Разность a≡b должна быть числом, кратным p,q,s. и, следовательно должна быть кратным h.

В частном случае, если модули p,q,s взаимно простые числа, то

a≡b mod (h),

Заметим, что можно допустить сравнения по отрицательным модулям, т.е. сравнение a≡b mod (p) означает и в этом случае, что разность a−b делится на p. Все свойства сравнений остаются в силе и для отрицательных модулей.