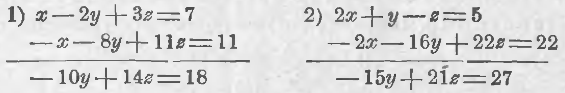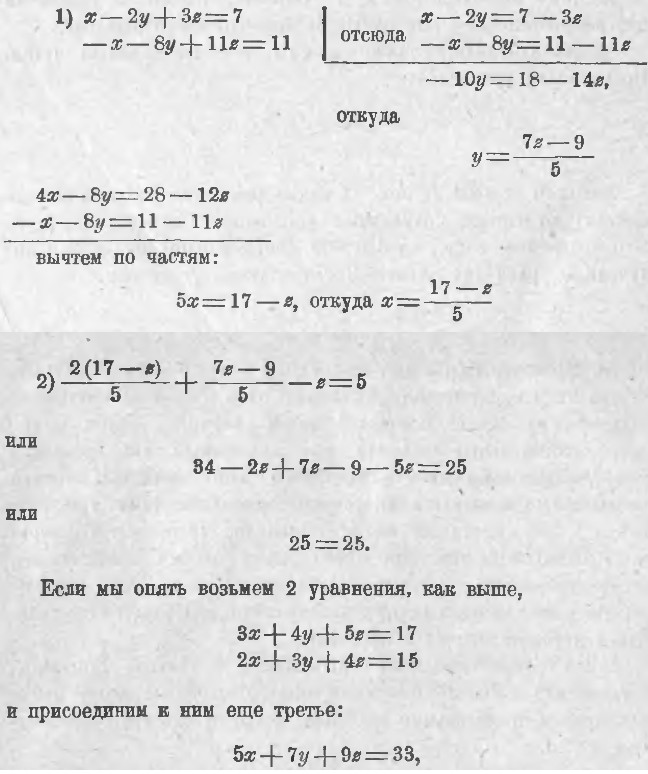Система уравнений с тремя неизвестными метод сложения

Видео:Решение систем уравнений методом сложенияСкачать

Системы линейных уравнений с тремя переменными

Линейным уравнением называется уравнение вида:

В этом уравнении — неизвестные, а — действительные (или комплексные) числа. При этом называются коэффициентами уравнения, а — свободным членом.

Рассмотрим систему трех линейных уравнений с тремя неизвестными:

Из трех способов решения этих систем: графического, способа подстановки и способа сложения остается два последних способа. Графический способ уже не проходит, так как пришлось бы находить точку пересечения трех плоскостей. А это трудно изобразить.

Способ подстановки для трех уравнений похож на способ подстановки для двух уравнений с двумя неизвестными, только у этого способа на один шаг больше. Первое: выражаем одно из неизвестных из одного уравнения через два остальных неизвестных и подставляем это выражение в оставшиеся два уравнения. Эти оставшиеся два уравнения составляют систему из двух уравнений с двумя неизвестными. А дальше решаем эту полученную систему и находим два неизвестных, а затем, зная их, и третье неизвестное.

Пример 1 Решить систему уравнений: способом подстановки.

Выразим из первого уравнения через остальные неизвестные и свободный член. Найденное выражение подставим в остальные уравнения.

Далее, оставляя первое уравнение в покое, решаем систему из двух получившихся уравнений с неизвестными и (предварительно разделив обе части второго уравнения на ).

Получили единственное решение системы

Рассмотрим теперь способ сложения. Так же как и для двух уравнений с двумя неизвестными, нужно при помощи сложения уравнений добиться, чтобы одно из неизвестных пропало.Приведем пример.

Пример 2 Решить систему уравнений: способом сложения.

Постараемся получить два уравнения с двумя неизвестными. Избавимся от неизвестной . Для этого удвоенное первое уравнение сложим почленно с удвоенным вторым уравнением, а удвоенное второе уравнение прибавим к третьему уравнению:

Далее производим почленное сложение двух уравнений с двумя неизвестными, исключая неизвестную :

Из последнего уравнения системы находим . Подставляя найденное значение во второе уравнение, находим . Наконец из первого уравнения находим . Итак — единственное решение системы.

В заключении решим задачу, которая приводится к системе с тремя неизвестными.

Задача В трех урнах — шариков. В первой урне шариков больше чем во второй на столько, сколько шариков в третьей урне. Число шариков во второй урне относится к числу шариков в третьей урне как . Сколько шариков в каждой урне?

Обозначим число шариков в 1-й, 2-й и 3-й урнах через соответственно. Тогда первое условие задачи дает уравнение , второе условие — , а третье условие — . Запишем три полученные уравнения в систему, сделав предварительно третье уравнение линейным:

Складывая почленно первые два уравнения находим .Решаем систему из двух оставшихся уравнений:

Итак, в урнах соответственно и шариков.

Длины волн инфракрасного света достаточно велики, чтобы перемещаться сквозь облака, которые в противном случае блокировали бы наш обзор. Используя большие инфракра сные телескопы, астрономы смогли заглянуть в ядро нашей галактики. Большое количество звезд излучают часть своей электромагнитной энергии в виде видимого света, крошечной части спектра, к которой чувствительны наши глаза.

Так как длина волны коррелирует с энергией, цвет звезды говорит нам, насколько она горячая. Используя телескопы, чувствительные к различным диапазонам длин волн спектра, астрономы получают представление о широком круге объектов и явлений во вселенной.

Пример №1 Постройте центральную симметрию тетраэдра, относительно точки O, изображенных на рисунке 3.

Для построения такой центральной симметрии сначала проведем через все точки тетраэдра прямые, каждая из которых будет проходить через точку O. На них построим отрезки, удовлетворяющие условиям |AO|=|A?O|, |BO|=|B?O|, |CO|=|C?O|, |DO|=|D?O| Таким образом, и получим искомую симметрию (рис. 4).

В ряду разных механических движений особенным значением обладают колебания. Это движения и процессы, имеющие периодичность во времени.

В среде электромагнитных явлений также значительное место заняли электромагнитные колебания. В этих колебаниях заряды, токи, электрические и магнитные поля изменяются согласно периодическим законам.

Совет №1 Велосипедист, имеющий скорость 300 м/с, или идеальный газ, оказывающий давление 100 паскалей в большой тепловой машине — это странно.

Нужна помощь с курсовой или дипломной работой?

Видео:Система с тремя переменнымиСкачать

Система линейных уравнений с тремя переменными

Линейное уравнение с тремя переменными и его решение

Уравнение вида ax+by+cz = d , где a, b, c, d — данные числа, называется линейным уравнением с тремя переменными x, y и z.

Например: $2x+5y+z = 8; -x+1, 5y+2z = 0; frac x-8y-5z = 7$

Уравнение с тремя переменными может быть не только линейным, т.е. содержать не только первые степени переменных x,y и z.

Например: $2x^2+xz+y^2+yz^2 = 3,x-5y^2+z^3 = 1, 7x^3+y+xyz = 7$

Решением уравнения с тремя переменными называется упорядоченная тройка значений переменных (x,y,z), обращающая это уравнение в тождество.

О тождествах – см. §3 данного справочника

Например: для уравнения 2x+5y+z=8 решениями являются тройки x = -2, y = 1, z = 7; x = -1, y = 1, 6 , z = 2; x = -3, y = 2, 4, z = 2 и т.д. Уравнение имеет бесконечное множество решений.

Геометрическим представлением линейного уравнения с тремя переменными является плоскость в трёхмерном координатном пространстве .

Решение системы линейных уравнений с тремя переменными методом подстановки

Алгоритм метода подстановки для системы уравнений с тремя переменными аналогичен алгоритму для двух переменных (см.§45 данного справочника)

Например: решить систему

$$ <left< begin 3x+2y-z = 8 \ x-y+z = -2 \ 2x-3y-5z = 1 end right.> Rightarrow <left< begin 3(y-z-2)+2y-z = 8 \ x = y-z-2 \ 2(y-z-2)-3y-5z = 1 end right.> Rightarrow $$

$$ Rightarrow <left< begin x = y-z-2 \ 5y-4z = 14 \ -y-7z = 5 end right.> Rightarrow <left< begin x = y-z-2 \ y = -7z-5 \ 5(-7z-5)-4z = 14 end right.> Rightarrow <left< begin x = y-z-2 \ y = -7z-5 \ -39z = 39 end right.> Rightarrow $$

$$ Rightarrow <left< begin x = 2-(-1)-2 = 1 \ y = -7cdot(-1)-5 = 2 \ z = -1 end right.> Rightarrow <left< begin x = 1 \ y = 2 \ z = -1 end right.> $$

Решение системы линейных уравнений с тремя переменными методом Крамера

Для системы с 3-мя переменными действуем по аналогии.

Дана система 3-х линейных уравнений с 3-мя переменными:

$$ <left< begin a_1 x+b_1 y+c_1 z = d_1 \ a_2 x+b_2 y+c_2 z = d_2 \ a_3 x+b_3 y+c_3 z = d_3 end right.> $$

Определим главный определитель системы:

$$ Delta = begin a_1 & b_1 & c_1 \ a_2 & b_2 & c_2 \ a_3 & b_3 & c_3 end $$

и вспомогательные определители :

$$ Delta_x = begin d_1 & b_1 & c_1 \ d_2 & b_2 & c_2 \ d_3 & b_3 & c_3 end, Delta_y = begin a_1 & d_1 & c_1 \ a_2 & d_2 & c_2 \ a_3 & d_3 & c_3 end, Delta_z = begin a_1 & b_1 & d_1 \ a_2 & b_2 & d_2 \ a_3 & b_3 & d_3 end $$

Тогда решение системы:

Соотношение значений определителей, расположения плоскостей и количества решений:

Три плоскости пересекаются в одной точке

Три плоскости параллельны

Две или три плоскости совпадают или пересекаются по прямой

Бесконечное множество решений

Осталось определить правило вычисления определителя 3-го порядка.

Таких правил несколько, приведём одно из них (так называемое «раскрытие определителя по первой строке»):

$$ Delta = begin a_1 & b_1 & c_1 \ a_2 & b_2 & c_2 \ a_3 & b_3 & c_3 end = a_1 = begin b_2 & c_2 \ b_3 & c_3 end — b_1 = begin a_2 & c_2 \ a_3 & c_3 end + c_1 = begin a_2 & b_2 \ a_3 & b_3 end = $$

$$ = a_1 (b_2 c_3-b_3 c_2 )-b_1 (a_2 c_3-a_3 c_2 )+c_1 (a_2 b_3-a_3 b_2 )$$

Примеры

Пример 1. Найдите решение системы уравнений методом подстановки:

$$<left< begin z = 3x+2y-13 \ 2x-y+3(3x+2y-13) = -2 \ x+2y-(3x+2y-13) = 9 end right.> Rightarrow <left< begin z = 3x+2y-13 \ 11x+5y = 37 \ -2x = -4 end right.> Rightarrow $$

$$Rightarrow <left< begin z = 3cdot2+2cdot3-13 = -1 \ y = frac = 3 \ x = 2 end right.> Rightarrow <left< begin x = 2 \ y = 3 \ z = -1 end right.> $$

$$ <left< begin x = -y-3z+6 \ 2(-y-3z+6)-5y-z = 5\ (-y-3z+6)+2y-5z = -11 end right.> Rightarrow <left< begin x = -y-3z+6 \ -7y-7z = -7 |:(-7) \ y-8z = -17 end right.> Rightarrow $$

$$ Rightarrow <left< begin x = -y-3z+6 \ y+z = 1 \ y-8z = -17 end right.> Rightarrow <left< begin x = -y-3z+6 \ 9z = 18 \ y = 1-z end right.> Rightarrow <left< begin x = 1-6+6 = 1 \ z = 2 \ y = 1-2 = -1 end right.> Rightarrow$$

Пример 2. Найдите решение системы уравнений методом Крамера:

$$ Delta = begin 3 & 2 & -1 \ 2 & -1 & 3\ 1 & 2 & -1 end = 3 = begin -1 & 3 \ 2 & -1 \ end — 2 = begin 2 & 3 \ 1 & -1 \ end — 1 = begin 2 & -1 \ 1 & 2 \ end = $$

$$ Delta_x = begin 13 & 2 & -1 \ -2 & -1 & 3 \ 9 & 2 & -1 \ end = 13 = begin -1 & 3 \ 2 & -1 \ end — 2 = begin -2 & 3 \ 9 & -1 \ end — 1 = begin -2 & -1 \ 9 & 2 \ end = $$

$$ Delta_y = begin 3 & 13 & -1 \ 2 & -2 & 3 \ 1 & 9 & -1 \ end = 3 = begin -2 & 3 \ 9 & -1 \ end — 13 = begin 2 & 3 \ 1 & -1 \ end — 1 = begin 2 & -2 \ 1 & 9 \ end = $$

$$ Delta_z = begin 3 & 2 & 13 \ 2 & -1 & -2 \ 1 & 2 & 9 \ end = 3 = begin -1 & -2 \ 2 & 9 \ end — 2 = begin 2 & -2 \ 1 & 9 \ end + 13 = begin 2 & -1 \ 1 & 2 \ end = $$

$$ Delta = begin 1 & 1 & 3 \ 2 & -5 & -1\ 1 & 2 & -5 end = 1 = begin -5 & -1 \ 2 & -5 \ end — 1 = begin 2 & -1 \ 1 & -5 \ end + 3 = begin 2 & -5 \ 1 & 2 \ end = $$

$$ Delta_x = begin 6 & 1 & 3 \ 5 & -5 & -1 \ -11 & 2 & -5 \ end = 6 = begin -5 & -1 \ 2 & -5 \ end — 1 = begin 5 & -1 \ -11 & -5 \ end + 3 = begin 5 & -5 \ -11 & 2 \ end = $$

$$ = 6(25+2)—(-25-11)+3(10-55) = 162+36-135 = 63 $$

$$ Delta_y = begin 1 & 16 & 3 \ 2 & 5 & -1 \ 1 & -11 & -5 \ end = 1 = begin 5 & -1 \ -11 & -5 \ end — 6 = begin 2 & -1 \ 1 & -5 \ end + 3 = begin 2 & 5 \ 1 & -11 \ end = $$

$$ Delta_z = begin 1 & 1 & 6 \ 2 & -5 & 5 \ 1 & 2 & -11 \ end = 1 = begin -5 & 5 \ 2 & -11 \ end — 1 = begin 2 & 5 \ 1 & -11 \ end + 6 = begin 2 & -5 \ 1 & 2 \ end = $$

Пример 3*. Решите систему уравнений относительно x,y,и z:

$$ a neq b, b neq c, a neq c $$

Решаем методом замены:

$$ <left< begin z = -(a^3+a^2 x+ay)\ b^3+b^2 x+by-(a^3+a^2 x+ay) = 0 \ c^3+c^2 x+cy-(a^3+a^2 x+ay) = 0 end right.> Rightarrow <left< beginz = -(a^3+a^2 x+ay)\ (b^2-a^2 )x+(b-a)y = a^3-b^3 \ (c^2-a^2 )x+(c-a)y = a^3-c^3 end right.> $$

Т.к. $ a neq b$ второе уравнение можно сократить на $(a-b) neq 0$

Т.к.$ a neq c$ третье уравнение можно сократить на $(a-с) neq 0 $. В третьем уравнении после сокращения поменяем знаки:

Из второго уравнения получаем:

Т.к. $b neq c$ можно сократить на $(b-c) neq 0$:

$$ z = -(a^3+a^2 x+ay) = -a^3+a^2 (a+b+c)-a(ab+ac+bc) = $$

$$ = -a^3+a^3+a^2 b+a^2 c-a^2 b-a^2 c-abc = -abc $$

Видео:Решение систем уравнений методом сложенияСкачать

Математика

67. Особенные случаи систем уравнений с тремя неизвестными . Возьмем следующую систему уравнений:

3x + 4y + 5z = 17
2x + 3y + 4z = 15
5x + 7y + 9z = 32

Наблюдательный человек здесь может подметить, что третье уравнение вовсе не является новым, а является следствием двух первых: каждый член 3-го уравнения получается от сложения соответствующих членов 1-го и 2-го уравнения (5x = 3x + 2x, 7y = 4y + 3y; 9z = 5z + 4z; 32 = 17 + 15), и само собою понятно, что если
3x + 4y + 5z должно равняться 17,
2x + 3y + 4z должно равняться 15,
то (3x + 4y + 5z) + (2x + 3y + 4z) должно равняться 32.

Поэтому мы здесь имеем, в сущности, только 2 уравнения с 3 неизвестными, и они имеют бесконечно много решений.

Можно составлять такие системы и более сложным путем. Возьмем два уравнения:

x – 2y + 3z = 7
2x + y – z = 5

Умножим каждое из них на какое-либо число и сложим (или вычтем) по частям полученные уравнения. Умножим обе части 1-го уравнения, например, на 3 и обе части второго на (–2) и полученные уравнения сложим. Тогда получим уравнения:

Это уравнение является следствием двух первых и поэтому все три уравнения, взятые вместе, должны иметь бесконечно много решений.

Попробуем решать эти уравнения: 1) из 1-го и 3-го сложением по частям исключим x; 2) из 2-го и 3-го, умножив предварительно третье на 2, также исключим x:

Если теперь разделить обе части 1-го из полученных уравнений на 2 и обе части 2-го на 3, то получим одно и то же уравнение, а именно:

Это обстоятельство и является признаком того, что наша система имеет бесконечно много решений.

Если мы изберем такой план: 1) из 1-го и, напр., 3-го уравнений определим x и y через z; 2) подставим полученные выражения в 3-е уравнение, то должны получить само собою очевидное равенство, вроде 0 = 0 или 7 = 7 или 15 = 15 или –11 = –11 и т. п.

то после предыдущего становится ясным, что эти 3 уравнения совместно решить нельзя. В самом деле, ведь левая часть 3-го уравнения получается от сложения левых частей 1-го и 2-го уравнений, а в таком случае эта сумма должна равняться 17 + 15 или 32, но не может равняться 33.

Также точно можно, взяв 2 уравнения произвольно, составить третье, несовместимое с ними, умножением каждого из взятых двух уравнений на какое-нибудь число и сложением (или вычитанием) полученных уравнений, причем известный член должно как-либо изменить. Например, если первое из взятых уравнений умножим на 2 (получим: 6x + 8y + 10z = 34), второе на 3 (получим: 6x + 9y + 12z = 45), сложим полученные уравнения по частям, но вторую часть как-либо изменим (напр., вместо получающейся суммы 79 возьмем 100), то полученное уравнение

12x + 17y + 22z = 100

не совместимо с первыми двумя.

Если кто-либо стал бы решать систему несовместимых уравнений, то пришел к результату явно нелепому, например:

📺 Видео

Как ЛЕГКО РЕШАТЬ Систему Линейный Уравнений — Метод СложенияСкачать

Решение системы линейных уравнений с двумя переменными способом сложения. 6 класс.Скачать

Система уравнений. Метод алгебраического сложенияСкачать

7 класс, 39 урок, Метод алгебраического сложенияСкачать

Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

Решение системы линейных уравнений с двумя переменными способом подстановки. 6 класс.Скачать

СИСТЕМЫ УРАВНЕНИЙ В ЕГЭ ЧАСТЬ I #shorts #математика #егэ #огэ #профильныйегэСкачать

9 класс, 11 урок, Методы решения систем уравненийСкачать

Решение системы уравнений методом ГауссаСкачать

Математика | Система уравнений на желтую звездочку (feat Золотой Медалист по бегу)Скачать

6 способов в одном видеоСкачать

Системы уравнений с тремя переменнымиСкачать

ПОСМОТРИ это видео, если хочешь решить систему линейных уравнений! Метод ПодстановкиСкачать

Решение систем линейных уравнений методом сложения - 7 класс. Как решать систему уравненийСкачать

Решение систем уравнений методом подстановкиСкачать

МЕТОД СЛОЖЕНИЯ | 7 класс алгебра | решение систем уравненийСкачать

Системы уравнений Метод сложения (вычитания)Скачать