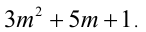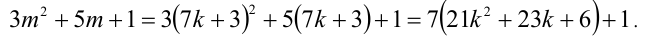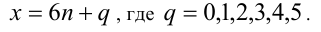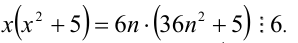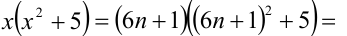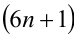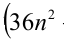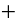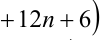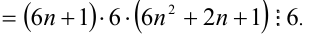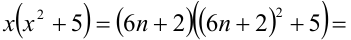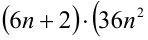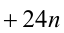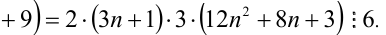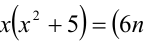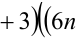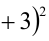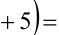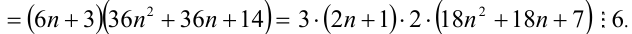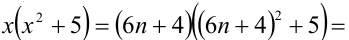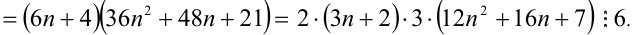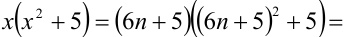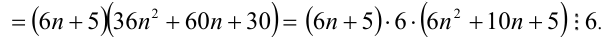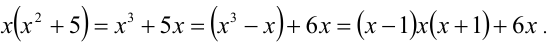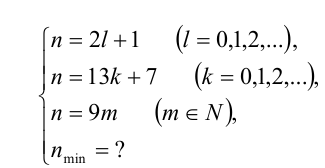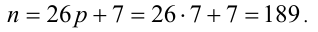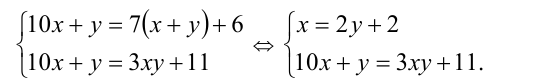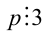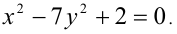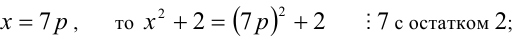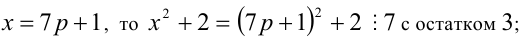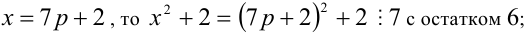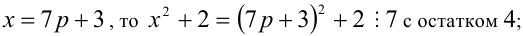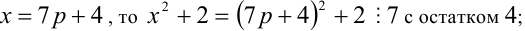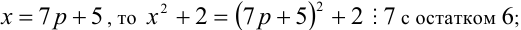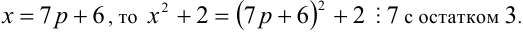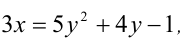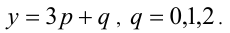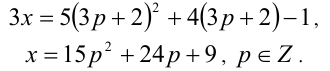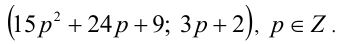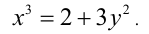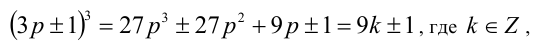Система уравнений с остатком от деления (4 видео)

Метод анализа остатков

Содержание

Метод анализа остатков
Пример №19.
Пример №20.
Пример №21.
Пример №22.
Пример №23.
Пример №24.
Пример №25.
Пример №26.
Пример №27.
Пример №28.
Пример №29.
Введение в модулярную арифметику
Прямое преобразование
Арифметические операции
Обратное преобразование
Задача №16. Поиск основания системы по окончанию числа, уравнения и различные кодировки, арифметические действия в различных системах.
📸 Видео

Метод анализа остатков

В основе метода анализа остатков, который используется при решении ряда задач с целочисленными неизвестными, лежит формула деления с остатком. Суть метода состоит в рассмотрении случаев различных остатков от деления на заданное число, что позволяет в конечном итоге решить поставленную задачу.

В первых трёх примерах, приведённых ниже, в явном виде ищутся остатки от деления одних целых чисел на другие.

Пример №19.

Найти частное и остаток от деления числа (— 23) на 7.

Решение:

Согласно формуле деления с остатком, получаем:

— 23 = — 4 • 7 + 5 , т.е. частное равно — 4, а остаток равен 5.

Пример №20.

Найти сумму остатков, получающихся при делении числа 7263544587435873 на 2, 4, 5, 9, 10, 25.

Решение:

Используя признаки делимости нацело на числа 2,4,5,9,10 и 25, находим остатки:

остаток от деления на 2 равен 1;
остаток от деления на4 равен 1;
остаток от деления на 5 равен 3;
остаток от деления на 9 равен 0;
остаток от деления на 10 равен 3;
остаток от деления на 25 равен 23.

Суммируя остатки 1 + 1+3+0+3+23, получаем в ответе 31.

Пример №21.

Пусть остаток от деления натурального числа m на 7 равен 3. Найти остаток от деления на 7 числа

Решение:

Из условия следует, что число m имеет вид: 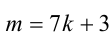. Тогда

Таким образом, остаток от деления числа 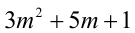на 7 равен 1.

Пример №22.

Доказать, что при любых целых X число 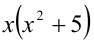делится нацело на 6.

Решение:

Разобьём множество всех целых X на 6 групп в зависимости от остатка при делении на 6, т.е. рассмотрим 6 случаев:

1) Пусть 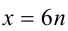, тогда

2) Пусть 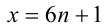, тогда

3) Пусть 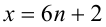, тогда

4) Пусть 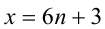, тогда

5) Пусть 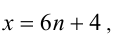тогда

6) Пусть 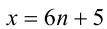, тогда

Таким образом, мы рассмотрели все целые числа X и доказали, что всегда (в каждом из шести случаев) выражение 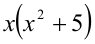кратно 6.

Замечание. Эту задачу можно было решить иначе. Преобразуем данное в условии задачи выражение:

Каждое из двух слагаемых делится нацело на 6 (первое как произведение трёх последовательных целых чисел), поэтому их сумма кратна 6.

Пример №23.

Учительница принесла в класс счётные палочки. Дети раскладывали их в пакетики. Когда разложили по 2 палочки в каждый пакетик, то осталась 1 лишняя палочка. Затем разложили по 13 штук в пакетик, и тогда осталось 7 лишних палочек. Когда же палочки разложили по 9 штук в пакетик, то лишних не осталось. Сколько, самое меньшее, было счётных палочек?

Решение:

Пусть всего было n счётных палочек. Тогда условия задачи приводят к системе

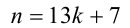
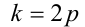
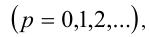
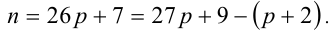
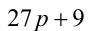
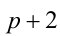
Таким образом, требуется найти наименьшее натуральное нечётное число п , делящееся на 9 и дающее при делении на 13 остаток 7. Заметим, что в силу нечётности число k должно быть чётным, т.е. причём меньшему n соответствует меньшее р , но тогда имеем Поскольку числа п и делятся нацело на 9, то, следовательно, число также должно быть кратно 9 (и при этом быть минимальным). Наименьшее целое неотрицательное р , для которого выполняются эти условия, равно 7, откуда находим

Ответ: самое меньшее — 189 счётных палочек.

Пример №24.

После деления некоторого двузначного числа на сумму его цифр получается 7 и в остатке 6. После деления этого же двузначного числа на произведение его цифр в частном получается 3 и в остатке 11. Найти это двузначное число.

Решение:

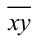
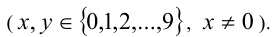
Обозначим — искомое число Тогда, по условию, имеем систему уравнений

Решая систему методом подстановки, находим единственное решение, удовлетворяющее всем условиям задачи: x= 8, y = 3 . Ответ: 83.

Пример №25.

Целые числа m, n,k не делятся нацело на 3. Доказать, что число 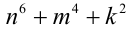делится на 3.

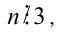
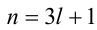
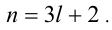
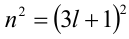
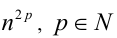
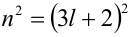
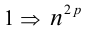
Доказательство. Если то возможны два случая: и . В первом случае — делится на 3 с остатком 1, а значит, , также делится на 3 с остатком 1. Аналогично во втором случае: делится на 3 с остатком делится на 3 с остатком 1. Таким образом, если целое число не делится нацело на 3, то его квадрат (любая чётная степень) при делении на 3 дают остаток 1. Но тогда сумма трёх таких чётных степеней кратна 3.

Пример №26.

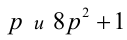
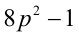
Доказать, что если — простые числа, то — тоже простое число.

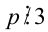
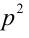
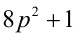
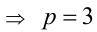
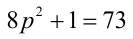
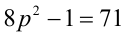
Доказательство. Если , то остаток от деления на 3 равен 1. Но тогда делилось бы на 3, что противоречит условию. Следовательно, , тогда действительно — простое число, и при этом тоже является простым.

Пример №27.

Решить уравнение в целых числах

Решение:

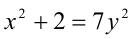
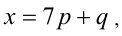
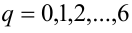
Перепишем уравнение в виде: . Заметим, что правая часть уравнения при любом целом Y делится нацело на 7. Выясним, какие остатки при делении на 7 даёт левая часть данного уравнения. Для этого разобьём множество всех целых X на 7 групп в зависимости от остатка при делении на 7: где , и рассмотрим каждый из этих случаев в отдельности.

1) Если

2) если

3) если

4) если

5) если

6) если

7) если

Итак, правая часть уравнения делится на 7 нацело (т.е. с остатком 0), а левая часть при этом — с остатками 2, 3, 4, 6. Однако равные числа при делении на одно и то же целое число 7 должны давать одинаковые остатки. Полученное противоречие говорит о том, что данное уравнение не имеет решений в целых числах.

Пример №28.

Найти все пары целых чисел (x;y), удовлетворяющие уравнению

и доказать, что для каждой такой пары сумма 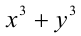является нечётным числом.

Решение:

Заметим, что левая часть уравнения кратна 3, следовательно, и правая часть должна делиться на 3 нацело. Разобьём множество всех целых y на три группы в зависимости от остатка при делении на 3:

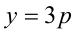
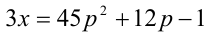
1) Если , то уравнение примет вид . Это равенство невозможно, так как его левая часть кратна 3, а правая — нет.

2) Если 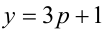, то получим аналогичную ситуацию.

3) Наконец, если 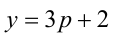, то, подставляя в уравнение, получим

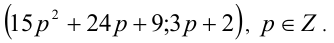
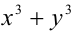
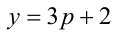
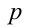
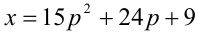
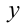
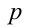
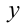
Следовательно, общий вид решений:Осталось показать, что — нечётно. В самом деле, если чётно, то — чётно и, значит, — нечётно. Если, наоборот, — нечётно, то также нечётно, а значит, — чётно. Таким образом, числа и , а значит и их кубы, имеют всегда разную чётность, поэтому их сумма есть нечётное число.

Ответ:

Пример №29.

Решить в целых числах уравнение

Решение:

Так как произвольное целое число представимо в виде , или где , а

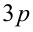
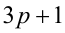
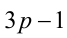
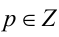
то любое число в кубе или делится нацело на 9, или даёт при делении на 9 в остатке 1 или 8. Аналогично, так как 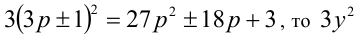даёт при делении на 9 остаток 0 или 3. Итак, правая часть уравнения может делиться на 9 с остатками 2 или 5, а левая — 0, 1 или 8. Следовательно, уравнение не имеет решений в целых числах.

Эта лекция взята со страницы, где размещён подробный курс лекций по предмету математика:

Эти страницы возможно вам будут полезны:

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

Видео:ЕГЭ по математике. Деление многочлена на двучленСкачать

Введение в модулярную арифметику

Для любой системы взаимно простых чисел p₁, … p_n, любое число X из диапазона [0; M), где M = p₁*p₂*…*p_n взаимооднозначно представимо в виде вектора (a₁, a₂, …, a_n), где a_i = X%p_i (здесь и далее «%» — операция взятия остатка от целочисленного деления X на p_i).
p₁, … p_n – модули системы
a₁, a₂, …, a_n – остатки (вычеты) числа по заданной системе модулей

На первый взгляд непонятно какое преимущество может дать такая система, однако существует 2 свойства, которые позволяют эффективно использовать модулярную арифметику в некоторых областях микроэлектроники:

Отсутствие переноса разрядов в сложении и умножении. Пусть нам дано два числа X₁ и X₂, представленные в виде системы остатков (x₁₁, x₁₂, …, x_1n) и (x₂₁, x₂₂, …, x_2n) по системе взаимнопростых чисел (p₁, p₂, …, p_n). В этом случае:
X₃ = X₁ + X₂ = ((x₁₁+x₂₁)%p₁, (x₁₂+x₂₂)%p₂, …, (x_1n+x_2n)%p_n)
X₄ = X₁ * X₂ = ((x₁₁*x₂₁)%p₁, (x₁₂*x₂₂)%p₂, …, (x_1n*x_2n)%p_n)
То есть что бы сложить или умножить два числа, достаточно сложить или умножить соответствующие элементы вектора, что для микроэлектроники означает, что это можно сделать параллельно и из-за малых размерностей p₁, p₂, …, p_n сделать очень быстро.
Ошибка в одной позиции вектора не влияет на расчеты в других позициях вектора. В отличие от позиционной системы счисления все элементы вектора равнозначны и ошибка в одном из них ведет всего лишь к сокращению динамического диапазона. Этот факт позволяет проектировать устройства с повышенной отказоустойчивостью и коррекцией ошибок.

Обычное умножение	Модулярное умножение

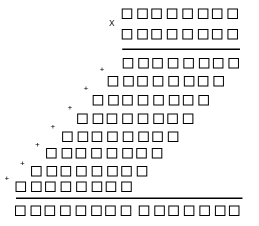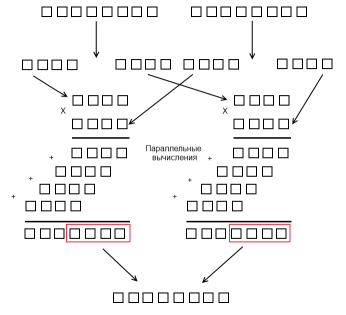Но не всё так гладко, как хотелось бы. В отличие от позиционной системы счисления, следующие операции (называемые «немодульными») выполняются сложнее, чем в позиционной системе счисления: сравнение чисел, контроль переполнения, деление, квадратный корень и.т.д. Первые успешные попытки применения модулярной арифметики в микроэлектронике были предприняты ещё в 1950-х годах, но из-за сложностей с немодульными операциями интерес несколько утих. Однако в настоящее время модулярная арифметика снова возвращается в микроэлектронику по следующим причинам:

большое распространение мобильных процессоров, в которых требуется высокая скорость при маленьком потреблении энергии. Отсутствие переноса в арифметических операциях сложения/умножения позволяет снизить потребление энергии.
увеличивающаяся плотность элементов на кристалле в некоторых случаях не позволяет провести полное тестирование, поэтому растет важность устойчивости процессоров к возможным ошибкам.
появление специализированных процессоров с большим числом операций над векторами, которые требуют высокой скорости и включают в себя преимущественно сложение и умножение чисел (как пример умножение матриц, скалярное произведение векторов, преобразования Фурье и.т.д).

В данный момент модулярная арифметика применяется в следующих областях: цифровая обработка сигналов, криптография, обработка изображений/аудио/видео и.т.д.

Видео:Как решать уравнения с остатком. Математика 5 классСкачать

Прямое преобразование

Прямое преобразование из позиционной системы счисления (обычно в двоичном виде) в систему счисления в остатках заключается в нахождении остатков от деления по каждому из модулей системы.

Пример: Пусть требуется найти представление числа X = 25 по системе модулей (3, 5, 7). X = (25%3, 25%5, 25%7) = (1, 0, 4).

Реализация нахождения вычета в микроэлектронике по заданному модулю строится на следующих свойствах вычетов:
(a+b) % p = (a%p + b%p)%p
(a*b) % p = (a%p * b%p)%p

Любое число X можно записать в виде X%p = (x_n-1*2 n-1 + x_n-2*2 n-2 + x₀*2 0 )%p = ((x_n-1)%p*2 n-1 %p) + ((x_n-2)%p*2 n-2 %p) + … + x₀%p)%p. Поскольку в данном случае x_n-1, … x₀ равны 0 или 1, то фактически нам требуется сложить вычеты вида (2 i %p).

Пример: пусть задано число 25 или в двоичной системе счисления 11001 и требуется найти остаток по модулю 7.
25%7 = (1*2 4 + 1*2 3 + 0*2 2 + 0* 1 + 1*2 0 )%7 = (2 4 %7 + 2 3 %7 + 1%7)%7 = (2 + 1 + 1)%7 = 4

Систему используемых модулей подбирают под конкретную задачу. Например, для представления 32-х битных чисел достаточно следующей системы модулей: (7, 11, 13, 17, 19, 23, 29, 31) – все они взаимнопросты друг с другом, их произведение равно 6685349671 > 4294967296. Каждый из модулей не превышает 5 бит, то есть операции сложения и умножения будут производиться над 5-битными числами.
Особое значение так же имеет система модулей вида: (2 n -1, 2 n , 2 n +1) в связи с тем, что прямое и обратное преобразование для них выполняется простейшим образом. Что бы получить остаток от деления на 2 n достаточно взять последние n цифр двоичного представления числа.

Видео:Как работает процент () / остаток от деления в программировании?Скачать

Арифметические операции

Пример: пусть задана система модулей (3, 5, 7), то есть мы можем выполнять операции, результат которых не превышает 3*5*7 = 105. Умножим два числа 8 и 10.
8 = (8%3, 8%5, 8%7) = (2, 3, 1)
10 = (10%3, 10%5, 10%7) = (1, 0, 3)
8*10 = ((2*1)%3, (3*0)%5, (1*3)%7) = (2, 0, 3)
Проверяем
80 = (80%3, 80%5, 80%7) = (2, 0, 3)

Видео:9 класс, 11 урок, Методы решения систем уравненийСкачать

Обратное преобразование

Обратное преобразование из системы счисления в остаточных классах в позиционную систему счисления производится одним из двух способов:

На базе Китайской теоремы об остатках или системы ортогональных базисов
На базе полиадического кода (другие названия mixed-radix system, система, со смешанным основанием)

Остальные предложенные в различной литературе способы, по сути, являются смесью этих двух.

Способ, основанный на Китайской теореме об остатках, базируется на следующей идее:
X = (x₁, x₂, … x_n) = (x₁, 0, …, 0) + (0, x₂, …, 0) + … + (0, 0, …., x_n) = x₁*(1, 0, …, 0) + x₂*(0, 1, …, 0) + … + x_n*(0, 0, …, 1).
То есть для обратного преобразования требуется найти систему ортогональных базисов B1 = (1, 0, …, 0), B2 = (0, 1, …, 0), …, BN = (0, 0, …, 1). Эти вектора находятся один раз для заданного базиса, а для их поиска требуется решить уравнение вида: (M_i*b_i)%p_i = 1, где M_i = M/p_i, а b_i – искомое число. В этом случае позиционное представление B_i = M_i*b_i и
X = (x₁*(M₁*b₁) + x₂*(M₂*b₂) + … + x_n*(M_n*b_n))%M

Пример: пусть задана система модулей (3, 5, 7), найдем значения M_i и b_i (0 b₁ = 2
(21*b₂)%5 = 1 => b₂ = 1
(15*b₃)%7 = 1 => b₃ = 1
Теперь преобразуем какое-нибудь число в системе остаточных классов. Положим
X = (2, 3, 1) = (2*35*2 + 3*21*1 + 1*15*1)%105 = (140 + 63 + 15)%105 = 218%105 = 8

Минус этого метода заключается в том, что для обратного преобразования требуется умножение и сложение больших чисел (M₁, …, M_n), а так же операция взятия остатка по модулю большого числа M.

Видео:Задача #11.Найдите остаток от деления 10 в 2021 степени плюс 5 на 9.Скачать

Задача №16. Поиск основания системы по окончанию числа, уравнения и различные кодировки, арифметические действия в различных системах.

Перед тем, как приступить к решению задач, нам нужно понять несколько несложных моментов.

Рассмотрим десятичное число 875. Последняя цифра числа (5) – это остаток от деления числа 875 на 10. Последние две цифры образуют число 75 – это остаток от деления числа 875 на 100. Аналогичные утверждения справедливы для любой системы счисления:

Последняя цифра числа – это остаток от деления этого числа на основание системы счисления.

Последние две цифры числа – это остаток от деления числа на основание системы счисления в квадрате.

Например, . Разделим 23 на основание системы 3, получим 7 и 2 в остатке (2 – это последняя цифра числа в троичной системе). Разделим 23 на 9 (основание в квадрате), получим 18 и 5 в остатке (5 = ).

Вернемся опять к привычной десятичной системе. Число = 100000. Т.е. 10 в степени k– это единица и k нулей.

Аналогичное утверждение справедливо для любой системы счисления:

Основание системы счисления в степени k в этой системе счисления записывается как единица и k нулей.

1. Поиск основания системы счисления

Пример 1.

В системе счисления с некоторым основанием десятичное число 27 записывается в виде 30. Укажите это основание.

Решение:

Обозначим искомое основание x. Тогда .Т.е. x = 9.

Пример 2.

В системе счисления с некоторым основанием десятичное число 13 записывается в виде 111. Укажите это основание.

Решение:

Обозначим искомое основание x. Тогда

Решаем квадратное уравнение, получаем корни 3 и -4. Поскольку основание системы счисления не может быть отрицательным, ответ 3.

Ответ: 3

Пример 3

Укажите через запятую в порядке возрастания все основания систем счисления, в которых запись числа 29 оканчивается на 5.

Решение:

Если в некоторой системе число 29 оканчивается на 5, то уменьшенное на 5 число (29-5=24) оканчивается на 0. Ранее мы уже говорили, что число оканчивается на 0 в том случае, когда оно без остатка делится на основание системы. Т.е. нам нужно найти все такие числа, которые являются делителями числа 24. Эти числа: 2, 3, 4, 6, 8, 12, 24. Заметим, что в системах счисления с основанием 2, 3, 4 нет числа 5 (а в формулировке задачи число 29 оканчивается на 5), значит остаются системы с основаниями: 6, 8, 12,

Ответ: 6, 8, 12, 24

Пример 4

Укажите через запятую в порядке возрастания все основания систем счисления, в которых запись числа 71 оканчивается на 13.

Если в некоторой системе число оканчивается на 13, то основание этой системы не меньше 4 (иначе там нет цифры 3).

Уменьшенное на 3 число (71-3=68) оканчивается на 10. Т.е. 68 нацело делится на искомое основание системы, а частное от этого при делении на основание системы дает в остатке 0.

Выпишем все целые делители числа 68: 2, 4, 17, 34, 68.

2 не подходит, т.к. основание не меньше 4. Остальные делители проверим:

68:4 = 17; 17:4 = 4 (ост 1) – подходит

68:17 = 4; 4:17 = 0 (ост 4) – не подходит

68:34 = 2; 2:17 = 0 (ост 2) – не подходит

68:68 = 1; 1:68 = 0 (ост 1) – подходит

2. Поиск чисел по условиям

Пример 5

Укажите через запятую в порядке возрастания все десятичные числа, не превосходящие 25, запись которых в системе счисления с основанием четыре оканчивается на 11?

Решение:

Для начала выясним, как выглядит число 25 в системе счисления с основанием 4.

. Т.е. нам нужно найти все числа, не больше , запись которых оканчивается на 11. По правилу последовательного счета в системе с основанием 4,
получаем числа и . Переводим их в десятичную систему счисления:

3. Решение уравнений

Пример 6

Ответ запишите в троичной системе (основание системы счисления в ответе писать не нужно).

Переведем все числа в десятичную систему счисления:

Квадратное уравнение имеет корни -8 и 6. (т.к. основание системы не может быть отрицательным). .

Ответ: 20

4. Подсчет количества единиц (нулей) в двоичной записи значения выражения

Для решения этого типа задач нам нужно вспомнить, как происходит сложение и вычитание «в столбик»:

При сложении происходит поразрядное суммирование записанных друг под другом цифр, начиная с младших разрядов. В случае, если полученная сумма двух цифр больше или равна основанию системы счисления, под суммируемыми цифрами записывается остаток от деления этой суммы на основание системы, а целая часть от деления этой суммы на основание системы прибавляется к сумме следующих разрядов.

При вычитании происходит поразрядное вычитание записанных друг под другом цифр, начиная с младших разрядов. В случае, если первая цифра меньше второй, мы «занимаем» у соседнего (большего) разряда единицу. Занимаемая единица в текущем разряде равна основанию системы счисления. В десятичной системе это 10, в двоичной 2, в троичной 3 и т.д.

Пример 7

Сколько единиц содержится в двоичной записи значения выражения: ?

Представим все числа выражения, как степени двойки:

В двоичной записи двойка в степени n выглядит, как 1 и n нулей. Тогда суммируя и , получим число, содержащее 2 единицы: