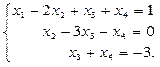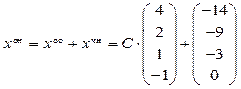Система уравнений с матрицей и вектором правых частей имеет вид

Матричный метод решения СЛАУ применяют к решению систем уравнений, у которых количество уравнений соответствует количеству неизвестных. Метод лучше применять для решения систем низкого порядка. Матричный метод решения систем линейных уравнений основывается на применении свойств умножения матриц.

Этот способ, другими словами метод обратной матрицы, называют так, так как решение сводится к обычному матричному уравнению, для решения которого нужно найти обратную матрицу.

Матричный метод решения СЛАУ с определителем, который больше или меньше нуля состоит в следующем:

Предположим, есть СЛУ (система линейных уравнений) с n неизвестными (над произвольным полем):

Значит, её легко перевести в матричную форму:

AX=B, где A — основная матрица системы, B и X — столбцы свободных членов и решений системы соответственно:

Умножим это матричное уравнение слева на A −1 — обратную матрицу к матрице A: A −1 (AX)=A −1 B.

Т.к. A −1 A=E, значит, X=A −1 B. Правая часть уравнения дает столбец решений начальной системы. Условием применимости матричного метода есть невырожденность матрицы A. Необходимым и достаточным условием этого есть неравенство нулю определителя матрицы A:

Для однородной системы линейных уравнений, т.е. если вектор B=0, выполняется обратное правило: у системы AX=0 есть нетривиальное (т.е. не равное нулю) решение лишь когда detA=0. Эта связь между решениями однородных и неоднородных систем линейных уравнений называется альтернатива Фредгольма.

Т.о., решение СЛАУ матричным методом производится по формуле . Либо, решение СЛАУ находят при помощи обратной матрицы A −1 .

Известно, что у квадратной матрицы А порядка n на n есть обратная матрица A −1 только в том случае, если ее определитель ненулевой. Таким образом, систему n линейных алгебраических уравнений с n неизвестными решаем матричным методом только в случае, если определитель основной матрицы системы не равен нулю.

Не взирая на то, что есть ограничения возможности применения такого метода и существуют сложности вычислений при больших значениях коэффициентов и систем высокого порядка, метод можно легко реализовать на ЭВМ.

Видео:Матричный метод решения систем уравненийСкачать

Пример решения неоднородной СЛАУ.

Для начала проверим, не равен ли нулю определитель матрицы коэффициентов у неизвестных СЛАУ.

Далее вычисляем алгебраические дополнения для элементов матрицы, которая состоит из коэффициентов при неизвестных. Эти коэффициенты нужны будут для вычисления обратной матрицы.

Теперь находим союзную матрицу, транспонируем её и подставляем в формулу для определения обратной матрицы.

Подставляем переменные в формулу:

Теперь находим неизвестные, перемножая обратную матрицу и столбик свободных членов.

При переходе от обычного вида СЛАУ к матричной форме будьте внимательными с порядком неизвестных переменных в уравнениях системы. Например:

НЕЛЬЗЯ записать как:

Необходимо, для начала, упорядочить неизвестные переменные в кадом уравнении системы и только после этого переходить к матричной записи:

Кроме того, нужно быть внимательными с обозначением неизвестных переменных, вместо x₁, x₂, …, x_n могут оказаться другие буквы. К примеру:

в матричной форме записываем так:

Матричным методом лучше решать системы линейных уравнений, в которых количество уравнений совпадает с числом неизвестных переменных и определитель основной матрицы системы не равен нулю. Когда в системе более 3-х уравнений, на нахождение обратной матрицы потребуется больше вычислительных усилий, поэтому, в этом случае целесообразно использовать для решения метод Гаусса.

Видео:Математика без Ху!ни. Метод Гаусса.Скачать

Основные определения и понятия

Рассмотрим систему m уравнений с n неизвестными

. (1)

Матрица A,составленная из коэффициентов при неизвестных системы, называется матрицей системы уравнений (1)

называют расширенной матрицей системы, ее последний столбец отделяют вертикальной чертой.

и .

называют соответственно вектором неизвестных и вектором правых частей системы (1). В этих обозначениях векторно-матричная запись системы (1) выглядит так:

(2)

Если вектор , то система называется однородной, если же (хотя бы один из элементов отличен от нуля), то система называется неоднородной.

Решением системы (1) называется такой вектор , что при подстановке чисел в систему (1) получаются верные равенства (тождества).

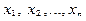
Система, имеющая хотя бы одно решение, называется совместной, в противном случае – несовместной.

Две системы называются эквивалентными, если множества их решений совпадают. Если к некоторому уравнению системы прибавить другое, умноженное на число, то решения системы не меняются. Заметим, что операции над системой уравнений сводятся к элементарным преобразованиям над расширенной матрицей . Таким образом, элементарные преобразования над не меняют совокупности ее решений.

Однородные системы

Рассмотрим однородную систему

(3)

Заметим, что однородная система всегда совместна, поскольку нуль-вектор – ее решение.

Вопрос лишь в том, единственно ли это решение и если нет, то что представляет собой совокупность всех ее решений.

Теорема. Множество всех решений однородной системы образует подпространство в

Действительно, если – решения системы (3), т.е. и , то , где – числа, также является решением системы (3):

.

Итак, решения однородной системы можно складывать, умножать на число, новый вектор вновь будет решением этой системы. Мы знаем, что в любом подпространстве (кроме ) можно выделить базис и любой вектор подпространства представить в виде линейной комбинации векторов базиса.

Обозначим V – подпространство решений однородной системы (3), а – некоторый базис в V.

Любой базис подпространства V решений однородной системы называют фундаментальной системой решений (ФСР).

Число векторов ФСР , где – число неизвестных системы (3), а r – ранг матрицы A. Таким образом, размерность подпространства решений .

Любой вектор-решение (общее решение) является линейной комбинацией векторов ФСР: .

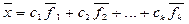
Научимся находить общее решение однородной системы. Для этого применяется метод Гаусса. Метод Гаусса для решения систем уравнений состоит из прямого и обратного хода. Прямым ходом заданную систему приводят к эквивалентной ступенчатой системе, которая легко поддается исследованию. Решение системы находится обратным ходом метода Гаусса.

Проиллюстрируем алгоритм метода на примере системы:

Все преобразования системы сводятся к преобразованиям матрицы системы.

Прямой ход метода Гаусса.

1. Приведем матрицы системы к ступенчатому виду:

Матрица ступенчатая, ее ранг .

2. Выпишем соответствующую систему уравнений:

.

Мы отбросили последнее уравнение, все коэффициенты которого равны нулю. Заметим, что угловые элементы матрицы являются коэффициентами при в ступенчатой системе.

3. Назовем переменные 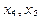, не связанные с угловыми элементами, свободными, а – зависимыми переменными (несвободными). Зависимыми переменными всегда объявляются переменные, коэффициентами которых являются угловые элементы. Заметим, что при другом способе приведения матрицы к ступенчатому виду свободными переменными могут оказаться переменные с другими индексами. Однако число свободных переменных всегда равно
В данном примере

Обратный ход метода Гаусса.

1. Выразим зависимые переменные через свободные из ступенчатой системы, начиная с последнего уравнения и «поднимаясь» вверх к первому. В результате получим

. (*)

Полученные выражения дают описание всего множества решений однородной системы (3). Давая свободным переменным произвольные значения (они играют роль параметров для множества решений) и вычисляя значения зависимых переменных, получаем некоторое частное решение системы. Так можно получить все решения системы, поэтому выражения (*) называют общим решением системы в координатной форме.

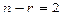
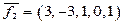
2. Запишем общее решение в векторной форме. Выберем из общего решения (*) линейно независимых решений и составим из них ФСР. Для этого придадим свободным переменным значения , тогда из (*) получим и ; затем , вычислим из (*) и .

Векторы линейно независимы (в силу выбора свободных переменных) и образуют ФСР.

Общее решение системы, записанное в векторной форме, имеет вид

.

Итак, размерность подпространства есть , где . Если (т.е. A имеет «полный ранг»), , т.е. имеет нулевую размерность ( ), а значит, состоит лишь из нулевого вектора . В этом случае однородная система имеет единственное нулевое (тривиальное) решение.

Неоднородные системы

Мы научились находить общее решение однородной системы. Перейдем теперь к неоднородным системам. Процедура получения общего решения (в координатной и векторной формах) для них будет похожей.

Пусть дана система или в координатной форме

.

Соответствующая этой системе однородная система имеет ту же матрицу системы , а вектор правых частей , т.е. .

Справедливо следующее утверждение.

Пусть – некоторое частное решение неоднородной системы , а – решение соответствующей однородной системы. Тогда вектор будет решением неоднородной системы. Действительно, .

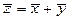
Это означает, что к решениям однородной системы можно прибавить решение неоднородной системы, в результате получим решение неоднородной системы.

Чтобы получить общее решение неоднородной системы, нужно к общему решению соответствующей однородной системы прибавить некоторое частное решениенеоднородной.

В отличие от однородной системы неоднородная не всегда совместна, поэтому прежде чем находить решение системы необходимо выяснить вопрос, существует ли хотя бы одно решение, т.е. совместна ли система. Ответ на этот вопрос дает теорема Кронекера-Капелли (критерий совместности неоднородной системы): система совместна тогда и только тогда, когда ранг основной матрицы A равен рангу расширенной матрицы .

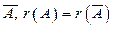
Рассмотрим метод Гаусса для решения неоднородной системы уравнений на примере системы

Прямой ход метода Гаусса.

1. Приведем расширенную матрицу системы к ступенчатому виду

Здесь , система совместна.

2. Запишем эквивалентную ступенчатую систему:

Переменные являются зависимыми, а – свободной переменной.

Обратный ход метода Гаусса.

1. Выразим зависимые переменные через свободные. Запишем общее решение неоднородной системы в координатной форме.

Выразим переменные через свободную переменную :

(*)

Полученные равенства задают общее решение исходной системы в координатной форме. Заметим, что для получения общего решения однородной системы нет нужды повторять заново всю процедуру. Достаточно в формулах (*) заменить свободные члены нулями. Получим общее решение однородной системы в координатной форме:

(**)

Размерность подпространства V решений однородной системы , а значит, ФСР содержит лишь один вектор. Найдем его из равенств (**), придавая свободной переменной любое отличное от нуля значение, например, пусть , тогда , , и базисный вектор .

Общее решение однородной системы в векторной форме выглядит так: , здесь – произвольная постоянная (сокращение «оо» означает общее «однородного»).

Остается найти частное решение неоднородной системы. Для этого в формулах (*) свободной переменной придадим произвольное (например, нулевое) значение, получаем: .

.

– общее решение в векторной форме.

Пример.

, ; ;

Таким образом, ранги расширенной и основной матриц системы не равны, теорема Кронекера-Капелли не выполняется, система несовместна. Итак, всякое решение неоднородной системы ( – «общее неоднородной») есть сумма частного решения неоднородной ( ) и общего решения однородной ( ): , или , где – фундаментальная система решений (базис подпространства решений однородной системы). Можно показать, что множество решений неоднородной системы не является подпространством (проверьте это самостоятельно). Множество представляет собой сдвиг пространства V на произвольный вектор . Результат сдвига не зависит от выбора частного решения .

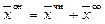
Говорят, что множество является «параллельным сдвигом» подпространства V. Понимать это нужно так: любой вектор – решение неоднородной системы может быть получен по формуле соответствующим подбором постоянных .

Видео:Математика без Ху!ни. Метод Гаусса. Совместность системы. Ранг матрицы.Скачать

Системы линейных алгебраических уравнений: основные понятия, виды

Видео:15. Однородная система линейных уравнений / фундаментальная система решенийСкачать

Определение СЛАУ

Системой линейных алгебраических уравнений (СЛАУ) называется система вида:

$$left<begin a_ cdot x_+a_ cdot x_+ldots+a_ cdot x_=b_ \ a_ cdot x_+a_ cdot x_+ldots+a_ cdot x_=b_ \ ldots ldots ldots ldots ldots ldots ldots ldots ldots ldots ldots ldots ldots ldots . . \ a_ cdot x_+a_ cdot x_+ldots+a_ cdot x_=b_ endright.$$

Упорядоченный набор значений $$left<x_^, x_^, ldots, x_^right>$$ называется решением системы, если при подстановке в уравнения все уравнения превращаются в тождество.

Задание. Проверить, является ли набор $$ решением системы $left<begin 3 x-2 y=-6 \ 5 x+y=3 endright.$

Решение. Подставляем в каждое из уравнений системы $x=0$ и $y=3$:

$$5 x+y=3 Rightarrow 5 cdot 0+3=3 Rightarrow 3=3$$

Так как в результате подстановки получили верные равенства, то делаем вывод, что заданный набор является решением указанной СЛАУ.

Ответ. Набор $$ является решением системы $left<begin 3 x-2 y=-6 \ 5 x+y=3 endright.$

Видео:ФСР. Система однородных уравнений. Общее решениеСкачать

Виды систем

СЛАУ называется совместной, если она имеет, хотя бы одно решение.

В противном случае система называется несовместной.

Система $left<begin 3 x-2 y=-6 \ 5 x+y=3 endright.$ является совместной, так как она имеет, по крайней мере, одно решение $x=0$, $y=3$

Система $left<begin 5 x+y=-6 \ 5 x+y=3 endright.$ является несовместной, так как выражения, стоящие в левых частях уравнений системы равны, но правые части не равны друг другу. Ни для каких наборов $$ это не выполняется.

Система называется определённой, если она совместна и имеет единственное решение.

В противном случае (т.е. если система совместна и имеет более одного решения) система называется неопределённой.

Система называется однородной, если все правые части уравнений, входящих в нее, равны нулю одновременно.

Система называется квадратной, если количество уравнений равно количеству неизвестных.

Система $left<begin 3 x-2 y=-6 \ 5 x+y=3 endright.$ квадратная, так как неизвестных две и это число равно количеству уравнений системы.

Видео:Решение матричных уравненийСкачать

Матричная запись систем уравнений

Исходную СЛАУ можно записать в матричном виде:

Задание. Систему $left<begin x-y+z-4 t=0 \ 5 x+y+t=-11 endright.$ записать в матричной форме и выписать все матрицы, которые ей соответствуют.

Решение. Заданную СЛАУ записываем в матричной форме $A. X=B$ , где матрица системы:

$$A=left(begin 1 & -1 & 1 & -4 \ 5 & 1 & 0 & 1 endright)$$

то есть, запись СЛАУ в матричной форме:

$$left(begin 1 & -1 & 1 & -4 \ 5 & 1 & 0 & 1 endright)left(begin x \ y \ z \ t endright)=left(begin 0 \ -11 endright)$$

Видео:Решение системы уравнений методом ГауссаСкачать

Расширенная матрица системы

Задание. Записать матрицу и расширенную матрицу системы $left<begin 2 x_+x_-x_=4 \ x_-x_=5 endright.$

Решение. Матрица системы $A=left(begin 2 & 1 & -1 \ 1 & -1 & 0 endright)$ , тогда расширенная матрица $tilde=(A mid B)=left(begin 2 & 1 & -1 & 4 \ 1 & -1 & 0 & 5 endright)$

Видео:Решение системы уравнений методом обратной матрицы.Скачать

Система линейных алгебраических уравнений. Основные термины. Матричная форма записи.

Видео:Система линейных уравнений. Метод обратной матрицы. Матричный метод.Скачать

Определение системы линейных алгебраических уравнений. Решение системы. Классификация систем.

Под системой линейных алгебраических уравнений (СЛАУ) подразумевают систему

содержащую $m$ уравнений и $n$ неизвестных ($x_1,x_2,ldots,x_n$). Прилагательное «линейных» означает, что все неизвестные (их еще называют переменными) входят только в первой степени.

Параметры $a_$ ($i=overline$, $j=overline$) называют коэффициентами, а $b_i$ ($i=overline$) – свободными членами СЛАУ. Иногда, чтобы подчеркнуть количество уравнений и неизвестных, говорят так «$mtimes n$ система линейных уравнений», – тем самым указывая, что СЛАУ содержит $m$ уравнений и $n$ неизвестных.

Если все свободные члены $b_i=0$ ($i=overline$), то СЛАУ называют однородной. Если среди свободных членов есть хотя бы один, отличный от нуля, СЛАУ называют неоднородной.

Решением СЛАУ (1) называют всякую упорядоченную совокупность чисел ($alpha_1, alpha_2,ldots,alpha_n$), если элементы этой совокупности, подставленные в заданном порядке вместо неизвестных $x_1,x_2,ldots,x_n$, обращают каждое уравнение СЛАУ в тождество.

Любая однородная СЛАУ имеет хотя бы одно решение: нулевое (в иной терминологии – тривиальное), т.е. $x_1=x_2=ldots=x_n=0$.

Если СЛАУ (1) имеет хотя бы одно решение, ее называют совместной, если же решений нет – несовместной. Если совместная СЛАУ имеет ровно одно решение, её именуют определённой, если бесконечное множество решений – неопределённой.

Имеем систему линейных алгебраических уравнений, содержащую $3$ уравнения и $5$ неизвестных: $x_1$, $x_2$, $x_3$, $x_4$, $x_5$. Можно, сказать, что задана система $3times 5$ линейных уравнений.

Коэффициентами системы (2) есть числа, стоящие перед неизвестными. Например, в первом уравнении эти числа таковы: 3, -4, 1, 7, -1. Свободные члены системы представлены числами 11, -65, 0. Так как среди свободных членов есть хотя бы один, не равный нулю, то СЛАУ (2) является неоднородной.

Упорядоченная совокупность $(4;-11;5;-7;1)$ является решением данной СЛАУ. В этом несложно убедиться, если подставить $x_1=4$, $x_2=-11$, $x_3=5$, $x_4=-7$, $x_5=1$ в уравнения заданной системы:

Естественно, возникает вопрос том, является ли проверенное решение единственным. Вопрос о количестве решений СЛАУ будет затронут в соответствующей теме.

Система (3) является СЛАУ, содержащей $5$ уравнений и $3$ неизвестных: $x_1$, $x_2$, $x_3$. Так как все свободные члены данной системы равны нулю, то СЛАУ (3) является однородной. Несложно проверить, что совокупность $(0;0;0)$ является решением данной СЛАУ. Подставляя $x_1=0$, $x_2=0$, $x_3=0$, например, в первое уравнение системы (3), получим верное равенство:

$$4x_1+2x_2-x_3=4cdot 0+2cdot 0-0=0.$$

Подстановка в иные уравнения делается аналогично.

Видео:Метод Крамера за 3 минуты. Решение системы линейных уравнений - bezbotvyСкачать

Матричная форма записи систем линейных алгебраических уравнений.

С каждой СЛАУ можно связать несколько матриц; более того – саму СЛАУ можно записать в виде матричного уравнения. Для СЛАУ (1) рассмотрим такие матрицы:

Матрица $A$ называется матрицей системы. Элементы данной матрицы представляют собой коэффициенты заданной СЛАУ.

Матрица-столбец $B$ называется матрицей свободных членов, а матрица-столбец $X$ – матрицей неизвестных.

Используя введённые выше обозначения, СЛАУ (1) можно записать в форме матричного уравнения: $Acdot X=B$.

Матрицы, связанные с системой, можно записать различными способами: всё зависит от порядка следования переменных и уравнений рассматриваемой СЛАУ. Но в любом случае порядок следования неизвестных в каждом уравнении заданной СЛАУ должен быть одинаков (см. пример №4).

Записать СЛАУ $ left < begin& 2x_1+3x_2-5x_3+x_4=-5;\ & 4x_1-x_3=0;\ & 14x_2+8x_3+x_4=-11. end right. $ в матричной форме и указать расширенную матрицу системы.

Имеем четыре неизвестных, которые в каждом уравнении следуют в таком порядке: $x_1$, $x_2$, $x_3$, $x_4$. Матрица неизвестных будет такой: $left( begin x_1 \ x_2 \ x_3 \ x_4 end right)$.

Свободные члены данной системы выражены числами -5, 0, -11, посему матрица свободных членов имеет вид: $B=left( begin -5 \ 0 \ -11 end right)$.

Перейдем к составлению матрицы системы. В первую строку данной матрицы будут занесены коэффициенты первого уравнения: 2, 3, -5, 1.

Во вторую строку запишем коэффициенты второго уравнения: 4, 0, -1, 0. При этом следует учесть, что коэффициенты системы при переменных $x_2$ и $x_4$ во втором уравнении равны нулю (ибо эти переменные во втором уравнении отсутствуют).

В третью строку матрицы системы запишем коэффициенты третьего уравнения: 0, 14, 8, 1. Учитываем при этом равенство нулю коэффициента при переменной $x_1$ (эта переменная отсутствует в третьем уравнении). Матрица системы будет иметь вид:

$$ A=left( begin 2 & 3 & -5 & 1\ 4 & 0 & -1 & 0 \ 0 & 14 & 8 & 1 end right) $$

Чтобы была нагляднее взаимосвязь между матрицей системы и самой системой, я запишу рядом заданную СЛАУ и ее матрицу системы:

В матричной форме заданная СЛАУ будет иметь вид $Acdot X=B$. В развернутой записи:

$$ left( begin 2 & 3 & -5 & 1\ 4 & 0 & -1 & 0 \ 0 & 14 & 8 & 1 end right) cdot left( begin x_1 \ x_2 \ x_3 \ x_4 end right) = left( begin -5 \ 0 \ -11 end right) $$

Запишем расширенную матрицу системы. Для этого к матрице системы $ A=left( begin 2 & 3 & -5 & 1\ 4 & 0 & -1 & 0 \ 0 & 14 & 8 & 1 end right) $ допишем столбец свободных членов (т.е. -5, 0, -11). Получим: $widetilde=left( begin 2 & 3 & -5 & 1 & -5 \ 4 & 0 & -1 & 0 & 0\ 0 & 14 & 8 & 1 & -11 end right) $.

Записать СЛАУ $ left <begin& 3y+4a=17;\ & 2a+4y+7c=10;\ & 8c+5y-9a=25; \ & 5a-c=-4. endright.$ в матричной форме и указать расширенную матрицу системы.

Как видите, порядок следования неизвестных в уравнениях данной СЛАУ различен. Например, во втором уравнении порядок таков: $a$, $y$, $c$, однако в третьем уравнении: $c$, $y$, $a$. Перед тем, как записывать СЛАУ в матричной форме, порядок следования переменных во всех уравнениях нужно сделать одинаковым.

Упорядочить переменные в уравнениях заданной СЛАУ можно разными способами (количество способов расставить три переменные составит $3!=6$). Я разберу два способа упорядочивания неизвестных.

Введём такой порядок: $c$, $y$, $a$. Перепишем систему, расставляя неизвестные в необходимом порядке: $left <begin& 3y+4a=17;\ & 7c+4y+2a=10;\ & 8c+5y-9a=25; \ & -c+5a=-4. endright.$

Матрица системы имеет вид: $ A=left( begin 0 & 3 & 4 \ 7 & 4 & 2\ 8 & 5 & -9 \ -1 & 0 & 5 end right) $. Матрица свободных членов: $B=left( begin 17 \ 10 \ 25 \ -4 end right)$. При записи матрицы неизвестных помним о порядке следования неизвестных: $X=left( begin c \ y \ a end right)$. Итак, матричная форма записи заданной СЛАУ такова: $Acdot X=B$. В развёрнутом виде:

$$ left( begin 0 & 3 & 4 \ 7 & 4 & 2\ 8 & 5 & -9 \ -1 & 0 & 5 end right) cdot left( begin c \ y \ a end right) = left( begin 17 \ 10 \ 25 \ -4 end right) $$

Расширенная матрица системы такова: $left( begin 0 & 3 & 4 & 17 \ 7 & 4 & 2 & 10\ 8 & 5 & -9 & 25 \ -1 & 0 & 5 & -4 end right) $.

Введём такой порядок: $a$, $c$, $y$. Перепишем систему, расставляя неизвестные в необходимом порядке: $left < begin& 4a+3y=17;\ & 2a+7c+4y=10;\ & -9a+8c+5y=25; \ & 5a-c=-4. endright.$

Матрица системы имеет вид: $ A=left( begin 4 & 0 & 3 \ 2 & 7 & 4\ -9 & 8 & 5 \ 5 & -1 & 0 end right)$. Матрица свободных членов: $B=left( begin 17 \ 10 \ 25 \ -4 end right)$. При записи матрицы неизвестных помним о порядке следования неизвестных: $X=left( begin a \ c \ y end right)$. Итак, матричная форма записи заданной СЛАУ такова: $Acdot X=B$. В развёрнутом виде:

$$ left( begin 4 & 0 & 3 \ 2 & 7 & 4\ -9 & 8 & 5 \ 5 & -1 & 0 end right) cdot left( begin a \ c \ y end right) = left( begin 17 \ 10 \ 25 \ -4 end right) $$

Расширенная матрица системы такова: $left( begin 4 & 0 & 3 & 17 \ 2 & 7 & 4 & 10\ -9 & 8 & 5 & 25 \ 5 & -1 & 0 & -4 end right) $.

Как видите, изменение порядка следования неизвестных равносильно перестановке столбцов матрицы системы. Но каким бы этот порядок расположения неизвестных ни был, он должен совпадать во всех уравнениях заданной СЛАУ.

Заметили ошибку, опечатку, или некорректно отобразилась формула? Отпишите, пожалуйста, об этом в данной теме на форуме (регистрация не требуется).

🌟 Видео

Решение систем уравнений второго порядка. 8 класс.Скачать

2 минуты на формулы Крамера ➜ Решение систем уравнений методом КрамераСкачать

Матан за час. Шпаргалка для первокурсника. Высшая математикаСкачать

Решение системы линейных алгебраических уравнений (СЛАУ) в Excel МАТРИЧНЫМ МЕТОДОМСкачать

Решение системы уравнений методом Крамера.Скачать

Решение системы уравнений методом Крамера 2x2Скачать

Математика это не ИсламСкачать

Обратная матрицаСкачать

Решение системы уравнений методом обратной матрицы - bezbotvyСкачать