При изучении основ электротехники приходится сталкиваться с необходимостью расчета тех или иных параметров различных схем. И самое простое, что приходится делать – это расчет токов ветвей в цепях постоянного тока.
Существует несколько наиболее применяемых методов расчетов для таких цепей: с помощью законов Кирхгофа, методом контурных токов, узловых потенциалов, методом эквивалентного генератора, эквивалентного источника тока, методом наложения. Для расчета более сложных цепей, например, в нелинейных схемах, могут применяться метод аппроксимации, графические методы и другие.
В данном разделе рассмотрим один из методов определения токов в цепи постоянного тока – метод узловых потенциалов.
- Метод узловых потенциалов примеры решения задач
- Уравнения узловых напряжений
- Содержание
- Описание
- Вывод уравнений узловых напряжений
- В прямоугольной системе координат
- В полярной системе координат
- Методы решения
- Расчёт электрических цепей по методу узловых потенциалов: методика
- Рекомендуемые записи
- Добавить комментарий Отменить ответ
- 🎦 Видео
Метод узловых потенциалов примеры решения задач
Для того, чтобы лучше разобраться в этом вопросе, рассмотрим конкретный пример схемы, показанной на рис.1.




Для начала обозначают направления токов в ветвях. Направление можно выбирать любым. Если в результате вычислений какой-то из токов получится с отрицательным значением, значит, его направление в действительности будет направлено в противоположную сторону относительно ранее обозначенного. Если в ветви имеется источник, то для удобства лучше обозначить направление тока в этой ветви совпадающим с направлением источника в этой ветви, хотя и не обязательно. Далее один из узлов схемы заземляем. Заземленный узел будет называться опорным, или базисным. Такой метод заземления на общее токораспределение в схеме влияния не оказывает.
Каждый из этих узлов будет обладать своим значением потенциала относительно узла 4. Именно значения этих потенциалов для дальнейшего определения токов и находят. Соответственно, для удобства этим потенциалам присваивают номера в соответствии с номером узла, т.е. φ1, φ2, φ3. Далее составляется система уравнений для оставшихся узлов 1, 2, 3.
В общем виде система имеет вид:
Использованные в этой системе уравнений буквенно-цифровые обозначения
имеют следующий смысл:





Аналогично находятся и остальные проводимости:
J11 – узловой ток узла 1, в котором участвуют ветви, подходящие именно к этому узлу, и содержащие в своем составе ЭДС. При этом, если ЭДС ветви, входящий в узел, направлена к рассматриваемому узлу (в данном случае к узлу 1), то такой узловой ток записывается с плюсом, если от узла, то с минусом. В данном случае
В результате всех ранее приведенных вычисленных значений исходная система уравнений примет вид:
Решать данную систему можно всеми доступными методами, мы же для упрощения решим ее в пакете Mathcad:
В результате получены следующие значения потенциалов в узлах цепи:
Токи в ветвях находятся в соответствии с законом Ома. Поясним это простыми словами.
В ветви с сопротивлением и источником, учитывая ранее обозначенное направление тока в рассматриваемой ветви, необходимо из потенциала узла, находящегося у начала стрелки направления тока, вычесть потенциал узла, находящегося у конца стрелки направления тока, а затем прибавить значение ЭДС в этой ветви. Далее все это разделить на сопротивление, имеющееся в ветви. Если бы ток и ЭДС в рассматриваемой ветви не совпадали по направлению, тогда значение ЭДС вычиталось. В ветви без ЭДС действует то же самое правило, только ЭДС в числителе, разумеется, отсутствует. В нашем примере получим, что
Значение тока первой ветви, как видно из расчета, получилось отрицательным. Значит, в действительности, этот ток направлен в противоположную сторону относительно его обозначенного направления на рис.1.
Правильность расчетов можно проверить, например, составлением баланса мощностей либо, к примеру, моделированием, схемы. Выполним моделирование в программе Multisim.

Как видим, результаты моделирования совпадают с расчетными значениями. Незначительная разница в тысячных долях из-за округлений промежуточных вычислений.
Видео:Метод узловых потенциалов. Самое простое и понятное объяснение этого методаСкачать

Уравнения узловых напряжений
Уравнения узловых напряжений (УУН) — система нелинейных (иногда линейных) алгебраических уравнений, в которых неизвестными являются напряжения в узлах электрической сети, наиболее часто применяемая для расчёта установившегося режима электрической сети.
Видео:Метод узловых потенциалов - определение токов. ЭлектротехникаСкачать

Содержание
Видео:Метод узловых и контурных уравненийСкачать

Описание
Установившийся режим электрических систем можно рассчитывать при различных способах задания исходных данных в зависимости от физической сути и цели расчёта. В статье рассмотрен наиболее часто встречающийся и наиболее простой случай, когда известны сопротивления и проводимости всех пассивных элементов электрической сети. Кроме того, заданы постоянные величины всех значений токов (мощности) во всех узлах, кроме балансирующего и все ЭДС, а также напряжение одного узла — базисного. При этом необходимо определить напряжения всех [math](n-1)[/math] узлов и токи во всех m ветвях.
В общем случае базисный по напряжению и балансирующий узлы могут не совпадать. Как правило, при расчётах режимов электрических систем предполагают, что эти узлы совпадают, в дальнейшем для простоты изложения предполагается, что базисным по напряжению и балансирующим является один и тот же [math]n[/math] -й узел. Число независимых уравнений по первому закону Кирхгофа равно числу независимых узлов [math](n-1)[/math] . Уравнение первого закона Кирхгофа для [math]n[/math] -го узла является следствием уравнений для остальных [math](n-1)[/math] узлов и не входит в число независимых уравнений.
Если в качестве неизвестных принять [math](n-1)[/math] узловых напря¬жений, то установившийся режим можно описать только узловыми уравнениями, вытекающими из первого закона Кирхгофа и закона Ома [1] , [2] , [3] , [4] . Уравнения узловых напряжений следуют из первого закона Кирхгофа, если все токи в ветвях выразить через узловые напряжения и проводимости ветвей. Число уравнений узловых напряжений равно числу независимых узлов [math](n-1)[/math] .
Уравнения баланса токов представляют собой простейшую форму уравнений, описывающих установившиеся режимы. Существуют две математические модели уравнений узловых напряжений:
Отличительной особенностью этих моделей является то, что линейная модель предполагает задание комплексных значений токов, в отличие от нелинейной модели, которая предполагает задание активной и реактивной мощностей. В большинстве задач нагрузки в узлах задаются активной и реактивной мощностями, по этой причине обычно используется нелинейная модель.
Видео:Лекция 020-4. Метод узловых напряженийСкачать

Вывод уравнений узловых напряжений
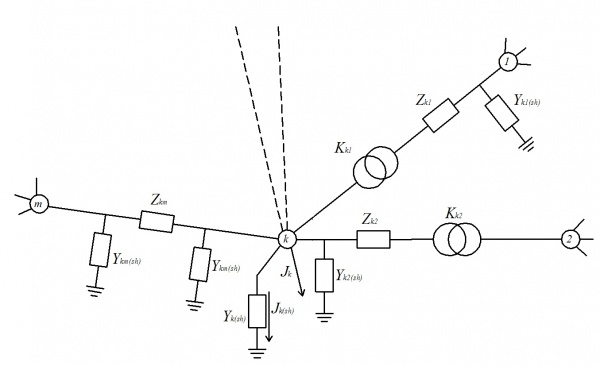
Для формирования УУН рассмотрим представленную на рис. 1 часть схемы замещения:
Первый закон Кирхгофа для к-го узла:
Наличие знака сопряжения в этом выражении обусловлено тем, что для идеального двухобмоточного трансформатора выполняется закон сохранения мощности [math]dot=dot=hatdot=hatdot[/math] , где индексами «Н» и «В» обозначены соответственно низшая и высшая обмотки трансформатора, поэтому, если [math]dot=dotdot<K_>[/math] , то из закона сохранения следует:
Подстановка полученных выражений в уравнение (1.1) с приведением подобных членов позволяет получить уравнение для k-го узла в виде:
Видео:Метод узловых потенциаловСкачать

В прямоугольной системе координат
В данной системе комплексные величины [math]displaystyle underline_, dot<U_>, dot<J_>[/math] представляются в виде
для проводимости справедливо следующее:
получаем, что [math]displaystyle underline=g-jb,[/math]
но для удобства расчёта матрицы проводимостей будем использовать соотношение
Запишем УУН для линейной ЭЭС:
левая часть данной системы характеризует токи, втекающие в k-й узел, правая часть — токи, вытекающие из того же узла, но с учетом влияния токов базы.
Подставляем (1), (2), (3) в (4), [math]dot_б[/math] представим аналогично уравнению (1), тогда имеем следующее:
[math]displaystyle begin sum_^ left( g_ + j b_ right) left( U_’ + j U_» right) = J_‘ + j J_»- left( g_ + j b_ right) left(U_’ + j U_»right), i = 1 ldots N end.[/math]
Сгруппируем и приведем подобные:
Сгруппируем относительно [math]j[/math] левую и правую части системы (5). Два комплексных числа равны, если равны их действительные и мнимые составляющие. Распишем в новой системе отдельно действительные и мнимые части. Получаем:
Представим данную систему (6) в матричной форме:
В случае, если [math]dot_б=U_б+j0,[/math] система (6) преобразуется к виду:
Соответственно упрощается матричная форма записи системы (8):
Вернемся к нелинейной модели ЭЭС. Для этого перенесем составляющую токов базы системы (4) в левую часть, изменив при этом диапазон [math]i=1 ldots (N-1)[/math] . Получаем:
Добавим, что [math]dot = P + j Q.[/math] (12)
Подставляем (11) в выражение (10), получаем следующее:
Подставляем (1), (3), (12) в (13), получаем:
[math]displaystyle begin sum_^ left( g_ + j b_ right) left( U_’ + j U_» right) = frac
, i = 1 ldots (N-1)end.[/math]
Раскрываем скобки, домножаем правую часть на сопряженное и группируем относительно [math]j[/math] :
Вынесем [math]j[/math] за знак суммы в левой части, а в правой части разобьем дробное выражение на две составляющие относительно [math]j[/math] , получим:
Преобразуем систему (14) к виду, аналогичному системе (8), и получаем нелинейную систему УУН для сети переменного тока в прямоугольных координатах в форме баланса токов:
Выведем систему нелинейных УУН для сети переменного тока в прямоугольных координатах в форме баланса мощностей. Для этого домножим систему (13) на [math]hat[/math] , получаем:
[math]displaystyle beginleft(U_i’-jU_i»right)sum_^left(g_+jb_right)left(U_’+jU_»right)=P_i-jQ_iend, i=1 ldots (N-1).[/math]
Вносим сопряженный комплекс напряжения под знак суммы и группируем относительно [math]j[/math] , имеем:
Преобразуем систему (17) к виду, аналогичному системе (15), и получаем нелинейную систему УУН для сети переменного тока в прямоугольных координатах в форме баланса мощностей:
Видео:Метод узловых напряжений.Этапы 1—4 (видео 17) | Анализ цепей | ЭлетротехникаСкачать

В полярной системе координат
Комплексное число можно представить в алгебраической, показательной и тригонометрической формах:
[math]displaystyle dot=U_k’+jU_k» = V_k cdot e^ = V_k big(cos(δ_k)+j sin(δ_k)big).[/math]
Для того, чтобы вывести УУН в форме баланса мощностей в полярной системе координат, необходимо в систему (16) подставить показательную запись комплексного числа [math]dot[/math] . Выполнив это, получим:
[math]displaystyle begin V_i e^ sum_ limits^ (g_ + j b_) cdot V_k cdot e^ = P_i — j Q_i end, i= overline.[/math]
Переносим экспоненты в одну сторону:
[math]displaystyle begin V_isum_limits^V_k(g_+jb_) cdot e^ cdot e^=P_i-jQ_iend, i= overline.[/math]
Используя свойство степеней, выполним преобразования:
[math]displaystyle begin V_isum_limits^ V_k (g_+jb_) cdot e^ = P_i — jQ_iend, i= overline.[/math]
Переходим к тригонометрической форме:
[math]displaystyle begin V_isum_limits^ V_k bigg( big(g_ + jb_ big) big( cos(δ_k-δ_i) + j cdot sin(δ_k-δ_i) big) bigg) = P_i-jQ_i end, i= overline.[/math]
Группируем относительно [math]j[/math] :
Преобразуем систему (19) к виду, аналогичному системе (15), и получаем нелинейную систему УУН для сети переменного тока в полярных координатах в форме баланса мощностей:
Видео:Метод контурных токов - определение токов. ЭлектротехникаСкачать

Методы решения
Основные методы решения системы уравнений узловых напряжений:
- Метод Гаусса-Зейделя — это один из самых первых разработанных методов. Обычно показывает более медленную сходимость по сравнению с другими итерационными методами. Основными особенности — это малое использование памяти и не требуется матричная алгебра.
- Метод Якоби.
- Метод Z-матриц.
- Метод Ньютона-Рафсона — один из самых популярных методов решения, основанный на разложении в ряд Тейлора.
- Метод голоморфного встраивания — прямой метод расчёта на основе комплексного анализа.
Видео:1 4 3 Метод узловых напряжениеСкачать

Расчёт электрических цепей по методу узловых потенциалов: методика
В дополнение к выводу метода рассмотрим методику расчёта электрических цепей по методу узловых потенциалов.
Воспользуйтесь программой онлайн-расчёта электрических цепей. Программа позволяет рассчитывать электрические цепи по закону Ома, по законам Кирхгофа, по методам контурных токов, узловых потенциалов и эквивалентного генератора, а также рассчитывать эквивалентное сопротивление цепи относительно источника питания.
Последовательность расчёта следующая.
- Пронумеровать все узлы и задать произвольное направление токов в схеме.
- Стянуть узлы с одинаковым потенциалом. Узлы будут иметь одинаковый потенциал, если между ними находится чистая ветвь с нулевым сопротивлением – закоротка (ветви между узлами 2 − 4 и 3 − 5 на рис. 1). Перерисовывать схему со стянутыми узлами не обязательно, но тогда следует учесть, что потенциалы узлов по концам закоротки будут одинаковыми.
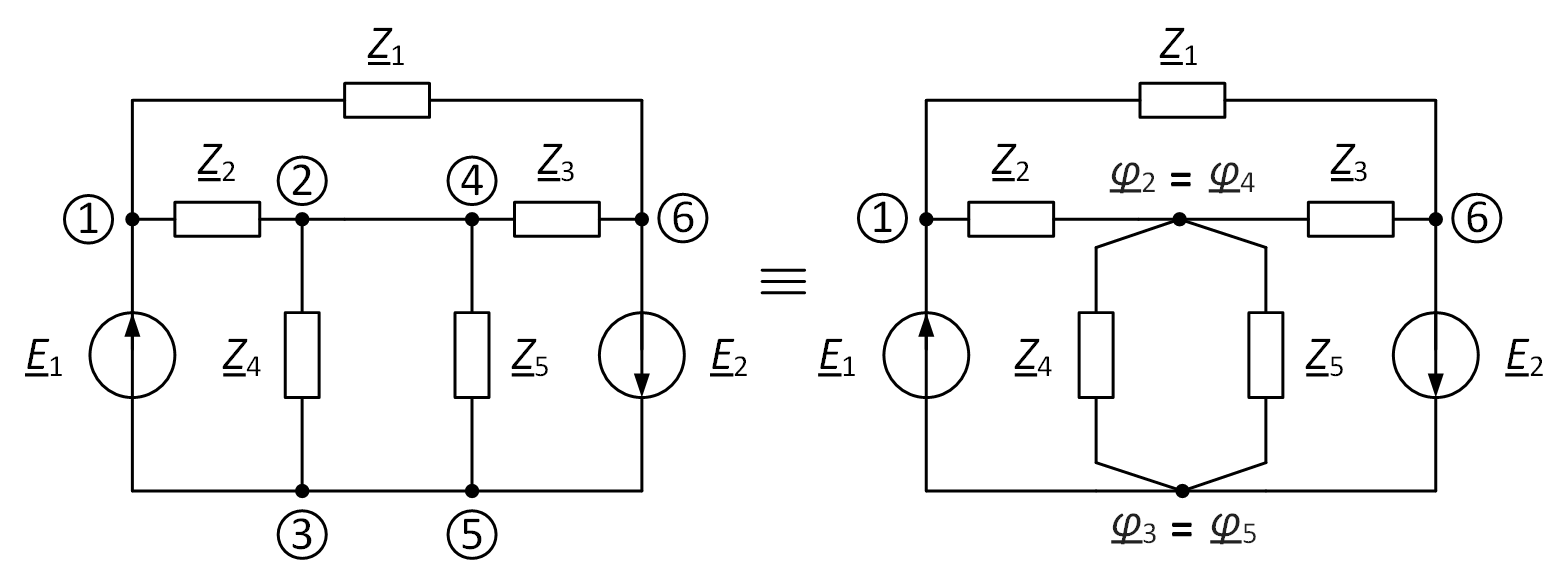
Рис. 1. Пример объединения узлов с одинаковым потенциалом
- Выбрать базисный узел (рис. 2) и приравнять его потенциал нулю $ underline_ = 0 space textrm $. В качестве базисного узла можно выбрать любой, за исключением случая, когда имеются особые ветви. Если в схеме есть хотя бы одна особая ветвь, то за базисный узел следует принимать один из концов одной из таких ветвей. При этом потенциал другого конца будет равен ЭДС $ underline_ = underline_ $, если источник напряжения направлен в этот узел, и равен минус ЭДС $ underline_ =- underline_ $, если источник направлен к базисному узлу.
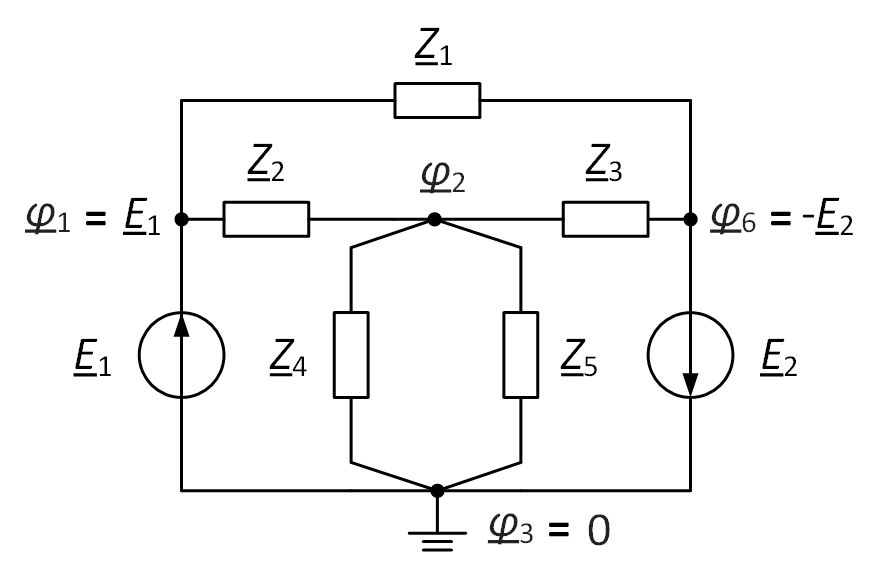
Рис. 2. Выбор базисного узла
Примечание. Зачастую для обозначения базисного узла используют символ заземления, так как принято считать, что «земля» имеет нулевой потенциал.
- Составить уравнения для узлов без особых ветвей, потенциалы которых неизвестны. Уравнения записываются по следующему принципу:
- потенциал рассматриваемого узла умножается на сумму проводимостей всех примыкающих к нему ветвей;
- вычитаются потенциалы узлов, находящихся на противоположных концах примыкающих ветвей, умноженные каждый на свою проводимость соединяющей их ветви;
- приравнивается алгебраической сумме примыкающих к данному узлу источников тока и источников ЭДС, последние умножаются на проводимость ветви, в которой они расположены.
Под алгебраической суммой подразумевается необходимость учёта направленности источников, если источник направлен в рассматриваемый узел, то он записывается со знаком «+», в противном случае со знаком «-».
В случае, если имеется более одной особой ветви, и они не имеют общие узлы, то уравнения для узлов, в состав которых входит особая ветвь, не примыкающая к базисному узлу, записываются следующим образом:
- потенциал рассматриваемого узла умножается на сумму проводимостей всех примыкающих к нему ветвей и проводимостей ветвей, примыкающих к узлу противоположного конца особой ветви;
- вычитаются потенциалы узлов, находящихся на противоположных концах примыкающих ветвей к узлам особой ветви, умноженные каждый на свою проводимость примыкающей ветви;
- приравнивается алгебраической сумме примыкающих к узлам особой ветви источников тока и источников ЭДС, последние умножаются на проводимость ветви, в которой они расположены, за исключением источника ЭДС особой ветви, который умножается на сумму проводимости ветвей, примыкающих к узлу противоположного конца особой ветви.
- При составлении уравнения проводимость особой ветви не учитывается ( 1 /0=∞). Следует также учитывать, что направление ЭДС особой ветви и соответственно её знак учитываются относительно рассматриваемого узла.
- Рассчитать токи в ветвях по закону Ома как алгебраическую сумму разности потенциалов и ЭДС в ветви с искомым током, делённую на сопротивление этой ветви. Вычитаемым будет тот потенциал, в который направлен ток, а знак ЭДС выбирается в зависимости от направления: в случае сонаправленности с током ЭДС берётся со знаком «+», в противном случае со знаком «-». Ток в закоротке следует искать по первому закону Кирхгофа, составленному для одного из узлов рассматриваемой ветви в исходной схеме, после расчета всех остальных токов в схеме.
- Правильность расчёта по методу узловых потенциалов проще всего проверить по первому закону Кирхгофа для уникальных узлов без особых ветвей, подставив полученные значения токов. Под уникальными узлами подразумеваются те узлы, при рассмотрении которых имеется хотя бы одна ветвь, не примыкающая к другим из рассмотренных узлов.
Пример решения. В качестве примера рассмотрим схему с двумя особыми ветвями и источником тока (рис. 3). Количество уравнений составляемых для нахождения узловых потенциалов равно
6 (всего узлов) – 1 (базисный узел) – 2 (узла особых ветвей) = 3.
Произвольно обозначим узлы и токи на схеме. Один из узлов одной из особой ветви (1-4 и 3-6) примем за базисный, к примеру узел 4, в таком случае $ underline_ = 0 $, а $ underline_ = underline_ $.
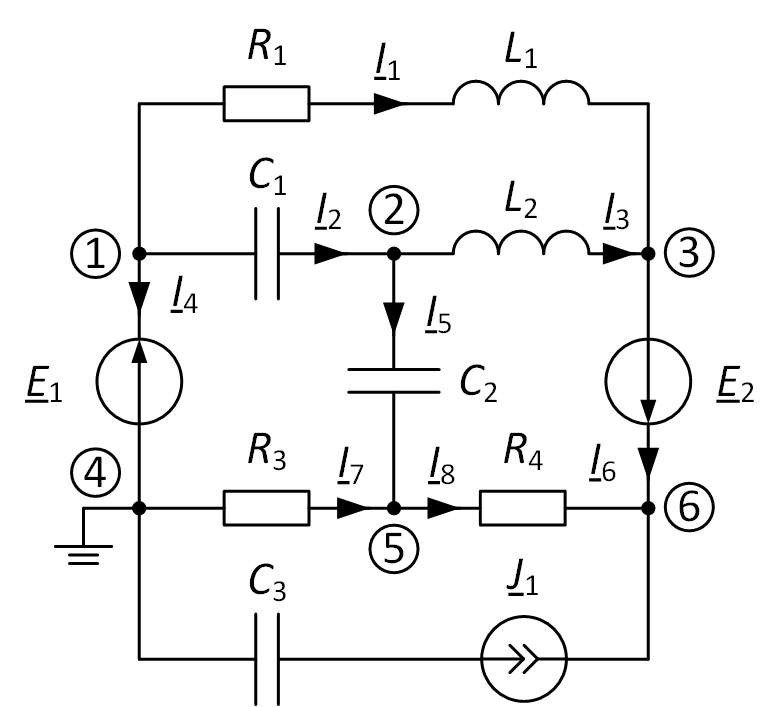
Рис. 3. Пример расчёта электрической схемы
В ветви 3-6 необходимо найти потенциал только одного из узлов (рассчитаем для узла 6), так как второй (потенциал узла 3) будет отличаться на значение ЭДС, т.е. $ underline_ = underline_- underline_ $. Далее необходимо составить уравнения для нахождения оставшихся потенциалов в узлах 2, 5 и 6. Следует отметить, что ёмкость ветви с источником тока не повлияет на расчёты, поскольку проводимость этой ветви бесконечно большая, а ток задаётся самим источником.
$$ begin underline_ cdot (underline_ + underline_ + underline_)- underline_ cdot underline_- underline_ cdot underline_- underline_ cdot underline_ = 0 \ underline_ cdot (underline_ + underline_ + underline_)- underline_ cdot underline_- underline_ cdot underline_- underline_ cdot underline_ = 0 \ underline_ cdot (underline_ + underline_ + underline_)- underline_ cdot underline_- underline_ cdot underline_- underline_ cdot underline_ = underline_ cdot (underline_ + underline_) + underline_ end $$
Подставим известные значения потенциалов, сократив количество неизвестных:
$$ begin underline_ cdot (underline_ + underline_ + underline_)- 0 cdot underline_- underline_ cdot underline_- underline_ cdot underline_ = 0 \ underline_ cdot (underline_ + underline_ + underline_)- underline_ cdot underline_- underline_ cdot underline_- (underline_- underline_) cdot underline_ = 0 \ underline_ cdot (underline_ + underline_ + underline_)- underline_ cdot underline_- underline_ cdot underline_- underline_ cdot underline_ = underline_ cdot (underline_ + underline_) + underline_ end $$
Перенесём все свободные составляющие в правую часть равенств и получим конечную систему уравнений с тремя неизвестными узловыми потенциалами:
$$ begin underline_ cdot (underline_ + underline_ + underline_)- underline_ cdot underline_- underline_ cdot underline_ = 0 \ underline_ cdot (underline_ + underline_ + underline_)- underline_ cdot underline_- underline_ cdot underline_ = underline_ cdot underline_- underline_ cdot underline_ \ underline_ cdot (underline_ + underline_ + underline_)- underline_ cdot underline_- underline_ cdot underline_ = underline_ cdot underline_ + underline_ cdot (underline_ + underline_) + underline_ end $$
Для решения системы уравнений с неизвестными узловыми потенциалами, можно воспользоваться Matlab. Для этого представим систему уравнений в матричной форме:
$$ begin underline_ + underline_ + underline_ & -underline_ & -underline_ \ -underline_ & underline_ + underline_ + underline_ & -underline_ \ -underline_ & -underline_ & underline_ + underline_ + underline_ end cdot begin underline_ \ underline_ \ underline_ end = \ = begin 0 \ underline_ cdot underline_- underline_ cdot underline_ \ underline_ cdot underline_ + underline_ cdot (underline_ + underline_) + underline_ end $$
Запишем скрипт в Matlab для нахождения неизвестных:
Примечание. Для решения в численном виде необходимо заменить символьное задание переменных реальными значениями проводимостей, ЭДС и тока источника.
В результате получим вектор-столбец $ underline<boldsymbol> $ из трёх элементов, состоящий из искомых узловых потенциалов, при этом токи в ветвях через потенциалы узлов:
Для проверки правильности расчёта можно воспользоваться уравнениями по первому закону Кирхгофа: если суммы токов в узлах 2 и 5 равны нулям, значит расчёт выполнен верно:
$$ underline_ + underline_- underline_ = 0, $$
$$ underline_ + underline_- underline_ = 0. $$
Итак, метод узловых потенциалов позволяет рассчитывать меньшее количество сложных уравнений для расчёта электрической цепи в сравнении с другими методами при меньшем числе узлов в сравнении с количеством контуров.
Рекомендуемые записи
Наряду с решением электрических схем по законам Кирхгофа и методом контурных токов используется метод узловых…
При исследовании электрических цепей и моделировании часто пользуются векторными диаграммами токов и напряжений. Под векторной…
При расчёте электрических цепей, помимо законов Кирхгофа, часто применяют метод контурных токов. Метод контурных токов…
Добавить комментарий Отменить ответ
Для отправки комментария вам необходимо авторизоваться.
Этот сайт использует Akismet для борьбы со спамом. Узнайте, как обрабатываются ваши данные комментариев.
🎦 Видео
Электротехника (ТОЭ). Лекция 5. Метод узловых потенциалов | Решение задачСкачать

Метод узловых потенциалов, задача 1Скачать

Урок 4. Расчет цепей постоянного тока. Законы КирхгофаСкачать

Метод узлового напряженияСкачать

Метод узловых потенциалов. Задача 2Скачать

Расчет электрической цепи постоянного тока методом узловых и контурных уравненийСкачать
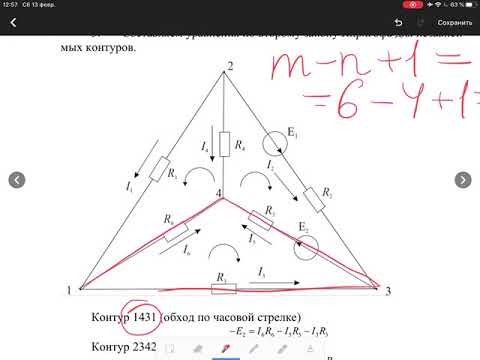
Законы Кирхгофа. Метод контурных уравненийСкачать

Метод узловых потенциаловСкачать

Метод узловых потенциалов. Решение задачи в программе mathcadСкачать

Метод узловых потенциалов. Как стать богом электрических цепей? | ЕГЭ 2024 по физикеСкачать

лекция 6. Метод узловых потенциалов.Скачать

Лекция 117. Правила КирхгофаСкачать