Система уравнений методом якоби онлайн

Видео:Метод простой итерации Пример РешенияСкачать

Решение СЛАУ методом простой итерации

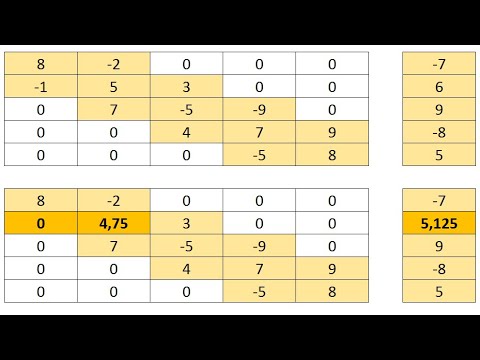
Назначение сервиса . Онлайн-калькулятор предназначен для решения СЛАУ методом простой итерации в онлайн режиме (см. пример решения). Для проверки решения генерируется шаблон в Excel .

• Шаг №1
• Шаг №2
• Видеоинструкция

Рассмотрим достаточные условия сходимости итерационной последовательности <x_n>.
Практически, для применения метода итерации систему линейных уравнений удобно «погрузить» в одну из трёх следующих метрик:
(3.4)
Для того, чтобы отображение F, заданное в метрическом пространстве соотношениями (3.2), было сжимающим, достаточно выполнение одного из следующих условий:
а) в пространстве с метрикой ρ₁: , т. е. максимальная из сумм модулей коэффициентов в правой части системы (3.2), взятых по строкам, должна быть меньше единицы.
б) в пространстве с метрикой ρ₂: , т. е. максимальная из сумм модулей коэффициентов в правой части системы (3.2), взятых по столбцам, должна быть меньше единицы.
в) в пространстве с метрикой ρ₃: , т. е. сумма квадратов при неизвестных в правой части системы (3.2) должна быть меньше единицы

Пример . Вычислить два приближения методом простой итерации. Оценить погрешность второго приближения. В качестве начального приближения выбрать x 0 =(0; 0; 0).

Так как диагональные элементы системы являются преобладающими, то приведем систему к нормальному виду:

Последовательные приближения будем искать по формулам:

Получаем:
x 1 =(-1.9022; 0.4889; 2.1456), x 2 =(-1.1720; 0.6315; 1.2389).
Для оценки погрешности в метрике ρ₁ вычисляем коэффициент μ
.
Вычисляем погрешность:

При большом числе неизвестных схема метода Гаусса, дающая точное решение, становится весьма сложной. В этом случае для решения СЛАУ иногда удобнее пользоваться методом простой итерации.

Видео:2.2 Итерационные методы решения СЛАУ (Якоби, Зейделя, релаксации)Скачать

Метод итераций для системы уравнений в Excel

Для вычисления точности epsilon .
Итерация №1: =ABS(B7)-ABS(B6);=ABS(C7)-ABS(C6);=ABS(D7)-ABS(D6)
Итерация №2: =ABS(B8)-ABS(B7);=ABS(C8)-ABS(C7);=ABS(D8)-ABS(D7)
Скачать шаблон решения.

Видео:Метод простых итераций пример решения нелинейных уравненийСкачать

Итерационные методы решения системы линейных алгебраических уравнений

В данной статье мы расскажем общие сведения об итерационных методах решения СЛАУ, познакомим с методом Зейделя и Якоби, а также приведем примеры решения систем линейных уравнений при помощи данных методов.

Видео:Метод Зейделя Пример РешенияСкачать

Общие сведения об итерационных методах или методе простой итерации

Метод итерации — это численный и приближенный метод решения СЛАУ.

Суть: нахождение по приближённому значению величины следующего приближения, которое является более точным. Метод позволяет получить значения корней системы с заданной точностью в виде предела последовательности некоторых векторов (итерационный процесс). Характер сходимости и сам факт сходимости метода зависит от выбора начального приближения корня x 0 .

Рассмотрим систему A x = b .

Чтобы применить итерационный метод, необходимо привести систему к эквивалентному виду x = B x + d . Затем выбираем начальное приближение к решению СЛАУ x ( 0 ) = ( x 1 0 , x 2 0 , . . . x m 0 ) и находим последовательность приближений к корню.

Для сходимости итерационного процесса является достаточным заданное условие В 1 . Окончание итерации зависит от того, какой итерационный метод применили.

Видео:Метод Ньютона (метод касательных) Пример РешенияСкачать

Метод Якоби

Метод Якоби — один из наиболее простых методов приведения системы матрицы к виду, удобному для итерации: из 1-го уравнения матрицы выражаем неизвестное x 1 , из 2-го выражаем неизвестное x 2 и т.д.

Результатом служит матрица В , в которой на главной диагонали находятся нулевые элементы, а все остальные вычисляются по формуле:

b i j = — a i j / a i i , i , j = 1 , 2 . . . , n

Элементы (компоненты) вектора d вычисляются по следующей формуле:

d i = b i / a i i , i = 1 , 2 , . . . , n

Расчетная формула метода простой итерации:

x ( n + 1 ) = B x ( x ) + d

Матричная запись (координатная):

x i ( n + 1 ) = b i 1 x n 1 + b i 2 x ( n ) 2 + . . . + b

Критерий окончания в методе Якоби:

x ( n + 1 ) — x ( n ) ε 1 , где ε 1 = 1 — B B ε

В случае если B 1 / 2 , то можно применить более простой критерий окончания итераций:

x ( n + 1 ) — x ( n ) ε

Решить СЛАУ методом Якоби:

10 x 1 + x 2 — x 3 = 11 x 1 + 10 x 2 — x 3 = 10 — x 1 + x 2 + 10 x 3 = 10

Необходимо решить систему с показателем точности ε = 10 — 3 .

Приводим СЛАУ к удобному виду для итерации:

x 1 = — 0 , 1 x 2 + 0 , 1 x 3 + 1 , 1 x 2 = — 0 , 1 x 1 + 0 , 1 x 3 + 1 x 3 = 0 , 1 x 1 — 0 , 1 x 2 + 1

Выбираем начальное приближение, например: x ( 0 ) = 1 , 1 1 1 — вектор правой части.

В таком случае, первая итерация имеет следующий внешний вид:

x 1 ( 1 ) = — 0 , 1 × 1 + 0 , 1 × 1 + 1 , 1 = 1 , 1 x 2 ( 1 ) = — 0 , 1 × 1 , 1 + 0 , 1 + 1 = 0 , 99 x 3 ( 1 ) = 0 , 1 × 1 , 1 — 0 , 1 × 1 + 1 = 1 , 01

Аналогичным способом вычисляются приближения к решению:

x ( 2 ) = 1 , 102 0 , 991 1 , 011 , x ( 3 ) = 1 , 102 0 , 9909 1 , 0111 , x ( 4 ) = 1 , 10202 0 , 99091 1 , 01111

Находим норму матрицы В , для этого используем норму B ∞ .

Поскольку сумма модулей элементов в каждой строке равна 0,2, то B ∞ = 0 , 2 1 / 2 , поэтому можно вычислить критерий окончания итерации:

x ( n + 1 ) — x ( n ) ε

Далее вычисляем нормы разности векторов:

x ( 3 ) — x ( 2 ) ∞ = 0 , 002 , x ( 4 ) — x ( 3 ) ∞ = 0 , 00002 .

Поскольку x ( 4 ) — x ( 3 ) ∞ ε , то можно считать, что мы достигли заданной точности на 4-ой итерации.

x 1 = 1 , 102 ; x 2 = 0 , 991 ; x 3 = 1 ,01 1 .

Видео:Математика без Ху!ни. Метод Гаусса.Скачать

Метод Зейделя

Метод Зейделя — метод является модификацией метода Якоби.

Суть: при вычислении очередного ( n + 1 ) — г о приближения к неизвестному x i при i > 1 используют уже найденные ( n + 1 ) — е приближения к неизвестным x 1 , x 2 , . . . , x i — 1 , а не n — о е приближение, как в методе Якоби.

x i ( n + 1 ) = b i 1 x 1 ( n + 1 ) + b i 2 x 2 ( n + 1 ) + . . . + b i , i — 1 x i — 2 ( n + 1 ) + b i , i + 1 x i + 1 ( n ) +

+ . . . + b i m x m ( n ) + d i

За условия сходимости и критерий окончания итераций можно принять такие же значения, как и в методе Якоби.

Решить СЛАУ методом Зейделя. Пусть матрица системы уравнений А — симметричная и положительно определенная. Следовательно, если выбрать начальное приближение, метод Зейделя сойдется. Дополнительных условий на малость нормы некоторой матрицы не накладывается.

Решим 3 системы уравнений:

2 x 1 + x 2 = 3 x 1 — 2 x 2 = 1 , x 1 + 2 x 2 = 3 2 x 1 — x 2 = 1 , 2 x 1 — 0 , 5 x 2 = 3 2 x 1 + 0 , 5 x 2 = 1

Приведем системы к удобному для итерации виду:

x 1 ( n + 1 ) = — 0 , 5 x 2 ( n ) + 1 , 5 x 2 ( n + 1 ) = 0 , 5 x 1 ( n + 1 ) + 0 , 5 , x 1 ( n + 1 ) = — 2 x 2 ( n ) + 3 x 2 ( n + 1 ) = 2 x 1 ( n + 1 ) — 1 , 2 x 1 — 0 , 5 x 2 = 3 2 x 1 + 0 , 5 x 2 = 1 .

Отличительная особенность, условие сходимости выполнено только для первой системы:

Вычисляем 3 первых приближения к каждому решению:

1-ая система: x ( 0 ) = 1 , 5 — 0 , 5 , x ( 1 ) = 1 , 75 0 , 375 , x ( 2 ) = 1 , 3125 0 , 1563 , x ( 3 ) = 1 , 4219 0 , 2109

Решение: x 1 = 1 , 4 , x 2 = 0 , 2 . Итерационный процесс сходится.

2-ая система: x ( 0 ) = 3 — 1 , x ( 1 ) = 5 9 , x ( 2 ) = — 15 — 31 , x ( 3 ) = 65 129

Итерационный процесс разошелся.

Решение: x 1 = 1 , x 2 = 2

3-я система: x ( 0 ) = 1 , 5 2 , x ( 1 ) = 2 — 6 , x ( 2 ) = 0 2 , x ( 3 ) = 0 2

Итерационный процесс зациклился.

Решение: x 1 = 1 , x 1 = 2

Видео:А.7.40 Метод Якоби поиска собственных векторов и значений симметричных матрицСкачать

Метод простой итерации

Если А — симметричная и положительно определенная, то СЛАУ приводят к эквивалентному виду:

x = x — τ ( A x — b ) , τ — итерационный параметр.

Расчетная формула имеет следующий внешний вид:

x ( n + 1 ) = x ( n ) — τ ( A x n — b ) .

Здесь B = E — τ A и параметр τ > 0 выбирают таким образом, чтобы по возможности сделать максимальной величину B 2 .

Пусть λ m i n и λ m a x — максимальные и минимальные собственные значения матрицы А .

τ = 2 / ( λ m i n + λ m a x ) — оптимальный выбор параметра. В этом случае B 2 принимает минимальное значение, которое равняется ( λ m i n + λ m a x ) / ( λ m i n — λ m a x ) .

Видео:Матричный метод решения систем уравненийСкачать

Система уравнений методом якоби онлайн

ADD THIS CALCULATOR ON YOUR WEBSITE:

Add Jacobian Calculator to your website to get the ease of using this calculator directly. Feel hassle-free to account this widget as it is 100% free, simple to use, and you can add it on multiple online platforms.

Download Jacobian Calculator App for Your Mobile, So you can calculate your values in your hand.

An online Jacobian calculator helps you to find the Jacobian matrix and the determinant of the set of functions. This Jacobian matrix calculator can determine the matrix for both two and three variables. So, let’s take a look at how to find the Jacobian matrix and its determinant.

Видео:Метод: Якоби, Зейделя, Ньютона(2 лекция)Скачать

What is the Jacobian matrix?

In calculus, the Jacobian matrix of a vector value function in multiple variables is the matrix of its first-order derivatives. The Jacobian matrix sums all the transformations of every part of the vector along with the coordinate axis. Usually, Jacobian matrixes are used to change the vectors from one coordinate system to another system.

Jacobian matrix of function (f) is defined to be a matrix (m x n), donated by J.

J = [ df/dx_1 …… dy/dx_n]

In other words, the Jacobian matrix of a function in multiple variables is the gradient of a scalar-valued function of a variable. If a function (f) is differentiable at a point, then its differential is given in the coordinates by the Jacobian matrix.

The jacobian matrix may be a square matrix with the same number of rows and columns of a rectangular matrix with a different number of rows and columns.

However, an Online Derivative Calculator helps to find the derivative of the function with respect to a given variable.

Jacobian Determinant:

If m = n, then f is a function from R^n to itself and the jacobian matrix is also known as a square matrix. And the determinant of a matrix is referred to as the Jacobian determinant.

The jacobian determinant at the given point provides information about the behavior of function (f). For example, the differentiable function (f) is invertible near the point P ER^n if the jacobian at point (p) is not zero.

Видео:8 Метод простой итерации Ручной счет Решение системы линейных уравнений СЛАУСкачать

How to Calculate Jacobian?

To calculate the Jacobian let’s see an example:

Example:

Jacobian matrix of [u^2-v^3, u^2+v^3] with respect to [x, y].

Solution:

Let’s find the Jacobian matrix for the equation:

We can find the matrix for these functions with an online Jacobian calculator quickly, otherwise, we need to take first partial derivatives for each variable of a function,

Jacobian Matrix is

Jacobian Determinant is

However, an Online Determinant Calculator helps you to compute the determinant of the given matrix input elements. This calculator determines the matrix determinant value up to 5×5 size of matrix.

Critical Points:

If f: R^n→R^mis a continuously differentiable function, then a critical point of a function f is a point where the rank of the jacobian matrix is not maximal. A point is critical when the jacobian determinant is equal to zero.

Видео:Решение системы уравнений методом ГауссаСкачать

How Jacobian Calculator Works?

An online Jacobian matrix calculator computes the matrix for the finite number of function with the same number of variables by following these steps:

Input:

• First, select the two or three vector value function.
• Now, substitute the values in the relevant fields.
• Hit the calculate button for results.

Output:

• The Jacobian calculator provides the matrix and its determinant with stepwise calculations.
• You can find the Jacobian matrix for two or three vector-valued functions Nemours time by clicking on recalculate button.

Видео:Метод Крамера за 3 минуты. Решение системы линейных уравнений - bezbotvyСкачать

FAQ:

What is Jacobian ratio?

Jacobian Ratio is the deviation of a given component from an ideally shaped component. The Jacobian value ranges from -1 to 1. If the jacobian range is equal to 1, then it represents a perfectly shaped component.

What is a Jacobian vector?

Jacobian is a matrix of partial derivatives. The matrix will have all partial derivatives of the vector function. The main use of Jacobian is can be found in the change of coordinates.

How we can find the inverse of Jacobian?

In a Cartesian manipulator, the inverse of the Jacobian is equal to the transpose of the Jacobian (JT = J^-1).

What is the negative Jacobian?

When the change of variables in reverse orientation, the Jacobian determinant is negative (-ve).

Is Jacobian matrix symmetric?

Usually, Jacobian matrixes (even the square ones) are not symmetric.

What is the rank of the Matrix?

In linear algebra, the rank of a matrix is the dimension of the vector space created by its columns. This corresponds to the number of linearly independent columns of the matrix.

Видео:Решение нелинейного уравнения методом простых итераций (программа)Скачать

Conclusion:

Use this online Jacobian calculator which is a defined matrix and determinant for the finite number of functions with the same number of variables. In the Jacobian matrix, every row consists of the partial derivative of the function with respect to their variables.

Видео:Решение систем линейных уравнений методом простой итерации в ExcelСкачать

Reference:

From the source of Wikipedia: Jacobian matrix and determinant, Inverse, Critical points, polar-Cartesian transformation.

From the source of ITCC Online: Definition of the Jacobian, Double Integration and the Jacobian, Integration and Coordinate Transformations, Jacobians and Triple Integrals.

From the source of SAS Online: JACOBIAN Statement, Jacobian matrix, Rosenbrock Function, GRADIENT statements.

💥 Видео

6. Количество итераций Метода Якоби. Вычислительная математика МФТИСкачать

Гальванические элементы. 1 часть. 10 класс.Скачать

Метод итераций решения СЛАУ с проверкой решения в ExcelСкачать

Метод итерацийСкачать

2.1 Точные методы решения СЛАУ (Крамера, Гаусса, Жордана, прогонки)Скачать

Лекция 4.005 по выч. методам ИВТ | Итерационные методы решения СЛАУ (форма Якоби). Метод Зейделя.Скачать