Система уравнений ламинарного пограничного слоя (8 видео)

Дифференциальные уравнения сжимаемого ламинарного пограничного слоя

Содержание

Дифференциальные уравнения сжимаемого ламинарного пограничного слоя
Ламинарный пограничный слой. Методы расчета ламинарного пограничного слоя
Страницы работы
Содержание работы
Г л а в а 2
ЛАМИНАРНЫЙ ПОГРАНИЧНЫЙ СЛОЙ
Пограничный слой
Общее понятие пограничного слоя
Ламинарный пограничный слой
Турбулентный пограничный слой
💥 Видео

Видео:3 Турбулентный и ламинарный отрыв пограничного слояСкачать

Дифференциальные уравнения сжимаемого ламинарного пограничного слоя

Для исследования процессов теплообмена не только на средних скоростях, но и в высокоскоростных потоках газа используется метод теории пограничного слоя(Глава 7). Таким же образом выводится система уравнений плоского (2-D) сжимаемого пограничного слоя (где плотность p-переменная). На основе анализа порядка величин из несжатых (p = const) (VI1-10) и (VII-316) уравнений (P-25 и P-26) и энергии (XI-16) получены следующие уравнения для сжимаемого пограничного слоя: уравнение движения для проекции на ось x (Си-17） проекция на ось Y Для сжимаемых 2D пограничных слоев уравнение неразрывности имеет следующий вид: д(Ри> х).?(П * М ДХ делать.

Уравнение энергии (Х1-18） сделайте dh. Необходимо добавить уравнение состояния в систему уравнений пограничного слоя. Для идеального газа форма (P-37) p = pRT. Теплоемкость c, коэффициент вязкости p и теплопроводность 1 зависят от температуры, поэтому вы должны знать следующее: Зависимости： с = с(7>、 Ч = Ч («1 = 1 (Д). (Си-20） Добавление граничных условий Γ к системе уравнений (XI-17, X1-18, XI-19, XI-20) и (П-37) дает замкнутую систему. Из 8 уравнений с 8 неизвестными.

Значимость этого уравнения (и его более общих вариантов) состоит в том, что оно представляет собой тот фундамент, на котором базируется весь математический аппарат. Людмила Фирмаль

Отметим еще одну важную особенность быстрого течения: абсолютная температура T должна содержаться в уравнении энергии пограничного слоя (XI-I9), а не в разнице температур F. Для умеренных скоростей течения(см. VI1-316) плотность p и физические константы p,1, c зависят от абсолютной температуры. Для дальнейшей работы требуется уравнение энергии для пограничного слоя иной формы, чем (XI-19). чтобы получить его, умножьте уравнение (X1-17) на скорость wₓ и добавьте результат к уравнению (XI-19 (Си-21） .

Полученное уравнение описывается для параметров пограничного слоя, а значения в скобках слева от него представляют температуру торможения пограничного слоя (см. уравнение XI-13). Учитывая X =и соотношение (XI-13), и игнорируя температурную зависимость числа растений, формула (XI-21) выражается в виде: Если Pr = 1, получим следующее ⁼⁽ХЬ23⁾ В результате исследования установлено, что если предположить, что ПР-1 в любой точке изолированной поверхности тела очищается высокоскоростным газовым потоком, то возникает застойная температура т0 (XI-13), причем не при понижающей температуре Тᵣ(X1-14), а при действительном состоянии ПР-1.

Поэтому предположение Pr = 1 значительно упрощает физическую ситуацию пограничного слоя. Поэтому именно формула (XI-23) выражает эту ситуацию. Необходимо обратить внимание на следующую ситуацию: уравнение энергии высокоскоростного потока (XI-23) может быть получено из уравнения энергии среднескоростного потока(VI1-36). в последнем избыточная температура O заменяется абсолютной температурой торможения TQ.

Очевидно, что этот факт очень важен в том смысле, что результат решения уравнения энергии потока средней скорости может быть расширен в случае быстрого течения, когда температура Φ заменяется на To на всех этапах решения. Конкретное решение уравнения энергии пограничного слоя при Pr = 1 Для уравнения энергии (XI-23) конкретное решение было найдено в виде[102） Т₀ = пост+ ^-= Конст. (Си-24） 2 воды Если сопротивление через пограничный слой не изменяет температуру, то выполняется уравнение энергии (XI-23).

Найти постоянную (XI-24), исходя из температуры потенциального потока, при условии, что температура внешней кромки пограничного слоя равна = Т’ОТ, РЕЗЮМЕ (Си-25） По всей толщине пограничного слоя скорость o> x уменьшается от скорости потенциального потока Hx на внешней кромке пограничного слоя до нуля стенки (^ I | y = o = 0), а термодинамическая температура T возрастает(XI-24), равная теплоизоляции стенки). Итак, если Pr = 1, то температура стенки равна (Си-26） .

Согласно закону Фурье, тепловой поток от теплопроводности пропорционален градиенту .Термодинамической temperature. In скоростной пограничный слой ламинарного течения можно найти, используя формулы (1-3) и (XI-25). Сре Ди Делать (Си-27） Из (X1-27) тепловой поток вблизи стенки (y = 0) равен нулю, так как здесь он равен 0. При 0 y 6 тепловой поток не равен нулю и направлен к внешнему краю пограничного слоя. СВ. Если > 0. Конкретное решение уравнения энергии (XI-25) позволяет проанализировать физическую ситуацию, возникающую в высокоскоростном ламинарном пограничном слое.

Однако удельное распределение скорости wx по температурам T и y неизвестно, поэтому информации, содержащейся в растворе (X1-25), недостаточно для определения теплового потока q (XI-27).Решение (XI-25) представляет собой градиент давления dr! Обратите внимание, что он действителен для любого значения DH. Конкретные решения уравнений пограничного слоя ПР = 1, др! дуплексный — ） Если температура торможения T0 и скорость wx линейно связаны, то установлено, что уравнение движения (XI-17) dr / dx = 0 и энергии (XI-23) удовлетворяют.

Из начал термодинамики следует, что полный дифференциал энтальпии имеет вид . Людмила Фирмаль

Два T₀= T + ^ =Awₓ+ B、 (ХІ-28） С. С. Где A и B-константы, определяемые с помощью границ Условие[102]. Температура и скорость линейно связаны и Pr-1, поэтому толщина динамического слоя 6 и теплового слоя D будет одинаковой. Определите константу в выражении (XI-28).Пограничный слой внешней кромке, температура потенциальный поток температуры, равной (см. диаграмму XI-2), в Т₀=Т₀>ooatwₓ=№х>₀О и То= ТВт atwₓ-0. Используя граничные условия (XI-28)、 И затем B = TW. Подставляя значения A и Bb(XI-28), получаем следующее: (Си-29） Учитывая (XI-9), мы представляем (XI-10) в виде: К ЛС… 1, г 1 _ г — — — 2 Вода КР переменного тока.

Помните » 2 Ш. сс. OI= Перепишите последнее отношение в виде (Си-30） Если сравнить (X1-28), (XI-29) и (XI-30), то можно увидеть связь между T и wₓ. Учитывая (XI-I1), можно представить (X1-31) в другом виде Т-м ^ — (т0, — JfzL МЛТ.(XI-32） Х> 2 МЕТЕОСВОДОК. О0 я. Теплопередача при Rg = 1, dr / dx = 0 сделайте производную Y (XI-3I)и подставьте результат в уравнение Фурье(1-3), получим уравнение теплового потока в виде: (Си-33） Здесь индекс относится к состоянию поверхности пластины. Анализируя формулу (XI-27), мы обнаружили, что в случае изолированной пластины тепловой поток направлен к внешнему краю пограничного слоя.

Однако на практике случаи неизолированных (для передачи тепла) плит встречаются очень часто. Анализируя формулу (XI-33), можно найти условия, определяющие направление теплового потока q. природа пограничного слоя такова, что условие dwjdy> 0 выполняется всегда, поэтому алгебраический код q зависит от знака квадратных скобок (XI-33). Если… (Си-34） Q имеет знак минус, и тепловой поток направлен от жидкости к стейку. Сервировочная (XI-34) тарелка называется холодной (рис. XI-3). Если… (^А) МК（-£-_ 1）、（XI-35) q имеет знак Далее тепловой поток направляется от стенки к жидкости.

Аналогии Рейнольдса Предыдущая Ч. VII,§ 6, обсуждалась гипотеза О. Рейнольдса о сходстве процессов передачи импульса и тепла в потоках несжимаемой жидкости (p = const).На этой основе были выведены формулы, определяющие коэффициент теплопередачи. Выясним, проводится ли аналогия Рейнольдса в высокоскоростном пограничном слое сжимаемого газа (переменная плотность p). Найти уравнение теплового потока с помощью (1-3) и (XI-32) Исключить из (XI-37) на основе равенства m = p В результате、 -На основании (XI-38) при 0 тепловой поток вблизи стенки равен X, OS 2-я часть уравнения (XI-39)、 ’AI press и Pr = 1 .

Согласно определению коэффициента трения, cf (VI1-25) условия свободного течения можно представить следующим образом: (Си-40） С (Си-39), коэффициент теплоотдачи а Подставьте значение (XI-40) в результирующую ratio. As итог、 При −2° ’ (Си-41） Учитывая (VI1-47), последняя формула может быть представлена следующим образом (ХІ-42） Полученное соотношение (XI-42) является математическим описанием аналогии Рейнольдса. Аналогичная зависимость была ранее получена для несжимаемых жидкостей (VI1-58). На основании (XI-42) можно утверждать, что аналогия Рейнольдса сохраняется в ламинарном пограничном слое сжимаемых жидкостей по крайней мере при Pr = 1.

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

Видео:Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

Ламинарный пограничный слой. Методы расчета ламинарного пограничного слоя

Страницы работы

Содержание работы

Видео:Урок гидравлики 16. Ламинарное и турбулентное течения Пограничный слойСкачать

Г л а в а 2

ЛАМИНАРНЫЙ ПОГРАНИЧНЫЙ СЛОЙ

2.1. Методы расчета ламинарного

прощающие допущения, положенные в основу вывода уравнений пограничного слоя, привели к тому, что стало возможным принимать давление поперек пограничного слоя постоянным: 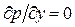,а давление вдоль стенки считать совпадающим с давлением внешнего течения и поэтому рассматривать его как заданную функцию. Эти обстоятельства сделали ненужным уравнение движения в направлении, перпендикулярном к стенке.

Хотя уравнения пограничного слоя значительно проще уравнений Навье – Стокса, все же в математическом отношении они остаются значительно трудными. Точные аналитические решения (с получением расчетных формул) выполнены лишь для сравнительно узкого класса задач, например для струи, см. [1].

Для решения более общих задач применяют численные методы. Если процесс вычисления становится очень трудоемким, имеет смысл попробовать решить задачу приближенными методами, например интегральными. Ниже мы рассмотрим некоторые из этих методов в приложении к задачам ламинарного пограничного слоя.

Автомодельные решения уравнений пограничного слоя. Упрощающие допущения, сделанные при выводе уравнений пограничного слоя, выполняются тем лучше, чем больше число Рейнольдса. Поэтому выясним, каким образом развитие пограничного слоя на заданном теле зависит от числа Рейнольдса. Уравнения движения пограничного слоя в безразмерном виде:

; (2.1)

. (2.2)

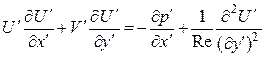
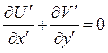
При этом граничными условиями будут:

U‘ = V‘ = 0при у’ = 0; 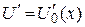при у = ¥.

Из уравнений (2.1) и (2.2) видим, что при заданной форме тела, а следовательно, при заданном потенциальном течении развитие пограничного слоя зависит от числа Rе.

Путем дальнейшего преобразования уравнений (2.1) и (2.2) можно привести их к такому виду, который не содержит числа Рейнольдса. В самом деле, положив

, получим вместо уравнений (2.1) и (2.2) следующие:

; (2.3)

; ( 2.4)

при у» = ¥.

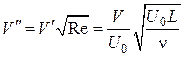
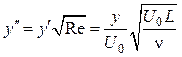
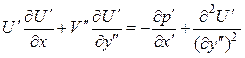
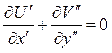
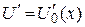
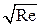
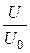
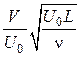
В уравнениях (2.3) и (2.4) число Rе отсутствует. Это означает, что решения системы уравнений (2.3) и (2.4) в координатах U‘(х’, у«) и V»(х’, у») также не зависят от числа Rе. Изменение числа Рейнольдса ведет за собой только аффинное преобразование пограничного слоя, изменяющее поперечную координату и скорость в поперечном направлении в раз. Иными словами, для заданного тела безразмерные составляющие скорости

и (2.5)

являются функциями безразмерных координат

и , так как

, (2.6)

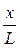
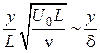
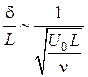
и эти функции в такой системе координат не зависят от числа Рейнольдса, или, как говорят, автомодельны по отношению к числу Рейнольдса (рис. 2.1).

Рис. 2.1. Пограничный слой на плоской стенке: а – схема течения;

в безразмерных координатах

Под автомодельными решениями уравнений пограничного слоя (в иностранной литературе часто используется термин «подобные решения») будем понимать такие, для которых продольная составляющая скорости обладает следующим свойством: профили скоростей U(х, у) в двух различных поперечных сечениях х отличаются один от другого только масштабом координат Uи у (см. рис. 2.1).

Следовательно, для автомодельных решений профили скоростей во всех сечениях х, перпендикулярных стенке, можно привести к совпадению, если построить их в безразмерном виде, разделив для этого координаты Uи у на соответствующие масштабы. Будем называть такие профили скоростей аффинно подобными профилями.

Приведенная схема развития пограничного слоя на пластине дает наглядное представление об этом. За масштаб скорости удобно принять скорость на внешней границе пограничного слоя U₀, тогда безразмерная скорость U/U₀ в каждом сечении будет изменяться от нуля до единицы. Масштабом для расстояния у в соответствии с соотношением (2.6) может служить некоторая величина, пропорциональная толщине пограничного слоя в рассматриваемом течении.

Вопрос об автомодельных решениях важен прежде всего с математической точки зрения. Если имеются подобные решения, то, как мы ниже увидим, дифференциальные уравнения пограничного слоя, представляющие собой систему уравнений в частных производных, могут быть сведены к одному обыкновенному дифференциальному уравнению, что в математическом отношении означает существенное упрощение.

Одним из примеров автомодельного в указанном смысле решения уравнений пограничного слоя является решение Блазиуса для плоской пластины.

2.2. Пограничный слой на плоской пластине.

Решение Блазиуса

Простейшим применением уравнений пограничного слоя является течение вдоль плоской пластины. Такое течение было исследовано Блазиусом, что явилось первой иллюстрацией применения уравнений Прандтля.

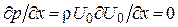
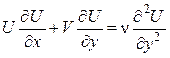
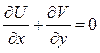
Так как в рассматриваемом случае скорость потенциального течения постоянна, U₀ = const, то согласно уравнению Бернулли . Тогда уравнения движения и неразрывности пограничного слоя принимают вид

; (2.7)

, (2.8)

причем граничными условиями будут

U = V = 0при у = 0; 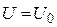при у = ¥.

В поставленной задаче обтекания бесконечной пластины нет характерной длины, поэтому можно предположить, что при определенным образом подобранных масштабах профили продольной скорости подобны между собой на различных расстояниях от передней кромки пластины.

Видео:Решение систем уравнений второго порядка. 8 класс.Скачать

Пограничный слой

Общее понятие пограничного слоя

Пограничный слой — область течения вязкой жидкости (газа) с малой по сравнению с продольными размерами поперечной толщиной, появляющаяся у поверхности обтекаемого твёрдого тела или у границы раздела двух потоков жидкости с разл. скоростями, температурамп или хим. составом. Возникновение пограничного слоя связано с явлением переноса в жидкости кол-ва движения, теплоты и массы, характеризуемых коэф. вязкости, теплопроводности и диффузии. Образование и развитие пограничного слоя можно проследить на примере динамического (скоростного) пограничного слоя поверхности
тела, обтекаемого потоком жидкостп или газа (рис. 1). Вследствие вязкости жидкости она «прилипает» к поверхности тела, т. е. на стенке продольная составляющая скорости жидкости раина нулю (если поверхность тела непроницаемая, то здесь равна пулю и поперечная составляющая скорости). Разрыв продольной составляющей скорости в вязкой жидкости существовать не может, поэтому возникает переходная область течения, т. е. пограничный слой, в к-ром происходит плавное изменение скорости от нуля на стенке до нек-рого конечного значения во внеш. потоке, где влияние вязкости исчезает.

Рис. 1. Профили скорости и температуры в пограничном слое на поверхности острого конуса в сверхзвуковом потоке газа.

Толщина такой переходной области и профиль скорости в ней определяются ур-ниями сохранения кол-ва движения. Помимо дпнамического пограничного слоя при обтекании тела можно выделить также тепловой (температурный) пограничный слой, образующийся в случае несовпадения температуры поверхности тела и температуры жидкости, а также концентрационный (диффузионный) пограничный слой, образующийся при протекании на стенке хим. реакции или же при вдуве инородного газа через проницаемую поверхность тела. В тепловом пограничном слое темп-pa жидкости непосредственно у стенки равна температуре поверхности тела. Если тело обтекается жидкостью с малой скоростью, то внутри теплового пограничного слоя происходит монотонное изменение температуры жидкости от температуры поверхности до температуры внеш. потока. Если же тело обтекается сверхзвуковым потоком газа, то внутри теплового пограничного слоя вследствие торможения газа и перехода кинетич. энергии во внутр. энергию молекул может возникать максимум температуры.
Другой часто встречающийся на практике случай пограничного слоя — это слой смешения, образующийся у границы струп, истекающей из сопла, напр. летат. аппарата с воздушно-реактивным или ракетным двигателем (рис. 2). В слое смешения скорость газа изменяется от скорости полёта до скорости истечения продуктов

Рис. 2. Слой смешения при истечении струи из сопла ракеты при полёте в атмосфере.

сгорания из сопла (в системе координат, связанной с летат. аппаратом), а темп-pa — от температуры атмосферы до температуры продуктов сгорания. Так же плавно изменяются концентрации компонент внеш. среды и продуктов сгорания.
Толщина динамического пограничного слоя определяется критерием Рейнольдса (см. Рейнольдса число Re), к-рый характеризует соотношение между инерц. силами и силами внутр. трения. Чем больше Re, тем меньше толщина пограничного слоя по сравнению с характерным размером тела. Обычно число Re намного превышает единицу, так что толщина пограничного слоя мала по сравнению с размерами тела. Кроме того, при этом оказывается несущественным изменение давления поперёк пограничного слоя. В результате параметры жидкости или газа на впеш. границе пограничного слоя могут быть определены так, как будто тело обтекается потоком идеальной (невязкой) жидкости. В более строгой постановке следует рассматривать обтекание идеальной жидкостью нек-рого эфф. тела, увеличенного на т. н. толщину вытеснения пограничного слоя. Это позволяет упростить методы расчёта трения и теплообмена между телом и обтекающей его жидкостью (газом). Для этого поток подразделяют на две части — область течения идеальной жидкости и тонкий пограничный слой у поверхности тела. Решая задачу об обтекании тела невязкнм потоком, находят распределение давления вдоль поверхности тела, а тем самым и давление в пограничномо слое. Течение внутри пограничного слоя рассчитывается после этого с учётом вязкости, теплопроводности и диффузии, что позволяет определить силы поверхностного трения и коэф. тепло- и массообмена.
Соотношение между толщинами динамич. и теплового пограничного слоя определяется Прапдтля числом Рr, а соотношение между толщинами динамич. и концентрац. пограничного слоя — Шмидта числом Sc. Для воды, воздуха и мн. др. непроводящих жидкостей и газов числа Рr и Sc близки к 1, вследствие чего толщины динамич., теплового и концентрационного пограничного слоя близки между собой.

Наличие вынужденного течения жидкости или газа не является обязательным для образования пограничного слоя у поверхности тела. Примером является пограничный слой образующийся у поверхности погружённого в жидкость тела или у стенок сосуда с жидкостью в случае свободной конвекции, возникающей при наличии разности температур жидкости и твёрдой стенки (рис. 3). В этом случае толщина пограничного слоя определяется Грасгофа числом Gr.

Рис. 3. Пограничный слой на стенках сосуда с жидкостью при подводе тепла сбоку.

Характер течения жидкости внутри пограничного слоя показывает, что при достаточно больших размерах тела (а точнее, при достаточно больших числах Re или Gr, рассчитываемых по длине тела) существуют два режима течения — ламинарное и турбулентное.

Ламинарный пограничный слой

В начальной части пограничного слоя течение является ламинарным, упорядоченным. Отд. частицы жидкости движутся по плавным траекториям, не пересекаясь и не перемешиваясь друг с другом. Форма этих траекторий близка к форме обтекаемого тела.
Днфференциальные уравнения течения вязкого теплопроводного однородного газа в ламинарном пограничном слое у поверхности тела произвольной формы могут быть получены нз Навье — Стокса уравнений, отбрасыванием членов, к-рые несущественны при достаточно больших числах Рейнольдса, когда толщина пограничного слоя мала по сравнению с размерами тела. Основы такого подхода были заложены Л. Прандтлем (L. Prandtl) в 1904. В случае стационарного двумерного течения эти упрощённые ур-ния На-вье — Стокса, известные как yp-ния пограничного слоя, или ур-ния Прандтля, представляют собой нелинейные днфференц. yp-ния параболич. типа и имеют вид: ур-нпе сохранения количества движения

ур-ние сохранения энергии

Здесь х и y — координаты, направленные вдоль поверхности тела и по нормали к ней, и и v — составляющие скорости вдоль этих координат, — плотность, р — давление, — козф. дпнамич. вязкости, Т — темп-pa, c_р — уд. теплоёмкость при пост. давлении, — коэф. теплопроводности.
Граничные условия к системе ур-ний (1) — (3) имеют вид: при y = 0 величины и = 0, v = v_w, Т = T_w; при yи Т T₁.
В случае смеси газов, в к-рой могут протекать хим. реакции, к ур-ниям (1) — (3) добавляются ур-ния неразрывности для отд. компонент

а ур-ние сохранения энергии удобнее записывать через энтальпию Н газа

где с_i — массовая концентрация i-й компоненты, Vi — скорость диффузии, w_i — массовая скорость образования i-й компоненты в единице объёма в результате хим. реакций, Н_i — энтальпия i-й компоненты и — теплота образования i-й компоненты при стандартных условиях. Скорость диффузии определяется градиентами концентраций отд. компонент (концентрац. диффузия), а также градиентом температуры (термодиффузия).
Для решения ур-ний пограничного слоя используются разл. методы, среди к-рых можно выделить две осн. группы — численные (конечно-разностные) и интегральные. Первая группа методов основана на численном интегрировании исходных ур-ний пограничного слоя методом сеток, или конечных разностей. Совр. ЭВМ позволяют это делать практически без внесения существенных упрощающих предположений, с учётом всех особенностей геометрии, физ—хим. процессов и т. п. Широкое распространение в численных расчётах получил анализ ур-ний пограничного слоя для разл. частных случаев, когда, вводя спец. переменные и опуская нек-рые несущественные члены, с одной стороны, получают упрощение исходной системы ур-ний, а с другой — сами результаты получаются в более обобщённом виде. К ним относятся разл. автомодельные решения, для к-рых имеет место понижение размерности задачи (напр., случай пограничного слоя на плоской пластине и конусе, в окрестности критич. точки затупленного тела, на клиновидных телах в дозвуковом потоке). См. Автомодельное течение.
Вторая группа методов основана на использовании уравнений пограничного слоя в интегральной форме. В этих ур-ниях в качестве зависимых переменных выступают нек-рые интегральные характеристики пограничного слоя: толщина вытеснения

толщина потери импульса

толщина потери энергии

(индексы «1» относятся к внеш. потоку, «01» — к границе пограничного слоя, «О» — к пограничному слою, а «w» — к обтекаемой поверхности). Интегральные ур-ния пограничного слоя получаются из дифференц. ур-ний типа (1) — (5) интегрированием последних по поперечной координате от 0 до внеш. границы пограничного слоя.

где — напряжение трения на поверхности тела, а — тепловой поток через его поверхность. Интегральные ур-ния позволяют учесть изменяющиеся условия течения вверх по потоку от рассматриваемой точки тела. Для решения интегральных ур-ний пограничного слоя (9) — (10) необходимо иметь сведения о профилях скорости и энтальпии (или температуры) внутри пограничного слоя. В основе различных приближённых методов решения ур-ний пограничного слоя лежит использование нек-рых наборов профилей скоростей и температур внутри пограничного слоя, напр. степенные профили. Знание профилей скорости и температуры позволяет связать между собой разл. характерные толщины пограничного слоя, входящие в ур-ния (9) — (10).

Турбулентный пограничный слой

По мере увеличения расстояния вдоль поверхности тела местное число Рейнольдса возрастает и начинает проявляться неустойчивость ламинарного течения по отношению к малым возмущениям. Такими возмущениями могут служить пульсации скорости во внеш. набегающем потоке, шероховатость поверхности и др. факторы. В результате ламинарная форма течения переходит в турбулентную, при этом на главное «осреднённое» движение жидкости или газа в продольном направлении накладываются хаотич., пульсац. движения отд. жидких конгломератов в поперечном направлении. В результате происходит интенсивное перемешивание жидкости, вследствие чего интенсивность переноса в поперечном направлении кол-ва движения, теплоты и массы резко увеличиваются. Потеря устойчивости и переход к турбулентному режиму течения внутри пограничного слоя происходят при нек-ром характерном числе Рейнольдса, к-рое наз. критическим. Величина Re_кр зависит от мн. факторов — степени турбулентности набегающего потока, шероховатости поверхности Маха числа М внеш. потока, относит. температуры поверхности, вдува или отсоса вещества через поверхность тела и др. Поскольку переход ламинарного режима течения в турбулентный связан с потерей устойчивости, то сам этот процесс не является достаточно стабильным, вследствие чего имеет место «перемежаемость» режима течения в пределах нек-рой области, к-рую называют областью перехода.
Изменение режима течения в пограничном слое сопровождается утолщением слоя и деформацией профилей скорости, температуры и концентраций. Одновременно возрастают коэф. поверхностного трения, тепло- и массообмена, а также изменяется характер их распределения вдоль поверхности тела (рис. 4).

Рис. 4. Изменение режима течения в пограничном слое и поверхностного трения на плоской пластине.

Течение внутри турбулентного пограничного слоя носит пульсационный, хаотич. характер: давление, плотность, скорость, темп-pa, концентрации и др. характеристики поля течения быстро изменяются, пульсируют, и притом хаотически. В этом случае при матем. описании течения каждый параметр можно представить в виде суммы осредпённого по времени, или среднего, значения и пульсационного. Напр.,Т =Интеграл по времени от пульсац. составляющей любого параметра за достаточно большой интервал времени (строго говоря, при) равен нулю

Однако осреднённые значения произведений пульсац. составляющих разл. параметров могут и не обращаться в нуль, что свидетельствует о корреляции между пульсациями. Именно корреляция между пульсациями разл. параметров объясняет нек-рый дополнит. механизм передачи кол-ва движения, энергии и диффузии в поперечном направлении.
Дифференц. ур-ния турбулентного пограничного слоя имеют тот же вид, что и ур-ния ламинарного пограничного слоя (1) — (5), с той лишь поправкой, что входящие в эти ур-ния коэф. вязкости, теплопроводности и диффузии представляются в виде суммы молекулярной и турбулентной составляющих. Вследствие наличия в этих ур-нпях турбулентных коэф. переноса вся система ур-ний турбулентного пограничного слоя оказывается незамкнутой. Поэтому для получения приближённых решений ур-нпй турбулентного пограничного слоя привлекаются дополнит. гипотезы и допущения. В частности, весьма плодотворной оказалась предложенная Л. Прандтлем гипотеза «пути перемешивания» l, позволяющая выразить коэф. турбулентной вязкостп через ср. плотность и градиент ср. скорости

С помощью аналогичных выражений могут быть представлены также коэф. турбулентной теплопроводности и коэф. турбулентной диффузии.
В общем случае турбулентный пограничный слой можно по высоте разделить на 3 области (рис. 5): пристеночный ламинарный подслой, где турбулентные пульсации затухаюти решающую роль играют молекулярные вязкость и теплопроводность; турбулентное ядро, в к-ром турбулентные вязкость и теплопроводность существенно превышают соответствующие молекулярные переносные свойства, и промежуточную переходную область. В результате многочисленных эксперпм. исследований установлено, что распределение скорости внутри турбулентного ядра описывается нек-рым универсальным эмпирич. законом

где — т. н. скорость сдвига, или динамич. скорость, а — кинематич. вязкость. Следует отметить, что логарифмич. закон распределения скорости внутри турбулентного ядра пограничного слоя может быть получен исходя из ф-лы Прандтля для турбулентной вязкости (11) в предположении, что входящий в эту ф-лу путь перемешивания l пропорц. расстоянию от стенки. При построении приближённых методов расчёта турбулентного пограничного слоя широко используются также степенные профили скорости и температуры

где Т₀, Т₀₁ и T_w — соответствующие температуры торможения в пограничном слое, на границе пограничного слоя и стенки. Значения показателей степени для дозвуковых скоростей изменяются от 1 /₇ до 1 /₉ при увеличении числа Рейнольдса и несущественно возрастают при больших числах Маха. В прикладных расчётах трения, тепло- и массообмена в турбулентном пограничном слое наиб. распространение получили полуэмпирич. методы, в частности метод, основанный на эксперим. данных по турбулентному трению на плоской пластине (аналогия процессов тепломассообмена и трения и введение понятия «эффективной длины»). Эксперпм. данные по турбулентному коэф. трения на плоской пластине, обтекаемой сверхзвуковым потоком, могут быть представлены аппроксимационной ф-лой

где — коэф. поверхностного трения, — число Рейнольдса, Т_е = Т₁ (1 + r (k — 1) М 2 /2) — равновесная темп-pa стенки, r — коэф. восстановления температуры, М₁ — число Маха внеш. потока, k = с_р/с_V — отношение теплоёмкостей при пост. давлении и пост. объёме.

Предположение об аналогии процессов тепломассообмена и трения, следующее из самого вида ур-ний пограничного слоя, позволяет для безразмерного коэф. теплообмена на пластине — Нуссельта числа Nu — записать ф-лу, к-рая хорошо согласуется с имеющимися эксперим. данными:

( — коэф. теплоотдачи, — коэф. теплопроводности газа на стенке). Для переноса этой зависимости на случай пограничного слоя на теле произвольной формы может быть использован предложенный В. С. Авдуевским метод «эффективной длины», предполагающий, что тепловой поток в рассматриваемой точке тела будет таким же, как в нек-рой точке на пластине при одинаковых местных параметрах течения и при условии, что в рассматриваемых точках тела и пластины толщины потери энергии (8) также одинаковы. Т. о., задача теплообмена сводится к определению эфф. длины пластины, для к-рой достигается необходимое значение толщины потери энергии. Если темп-pa стенки постоянна, то, напр., для осесимметричного тела при произвольном распределении давления вдоль поверхноста эфф. длина х_эф равна

где R — переменный радиус поперечного сечения тела, a u₁ — скорость жидкости или газа на внеш. границе пограничного слоя.

Рис. 5. Внутреннее строение турбулентного пограничного слоя.

Течение в пограничном слое оказывает решающее влияние на явление отрыва потока от поверхности обтекаемого тела как во внешних (напр., обтекание крыла), так и во внутренних (напр., течение в диффузоре) течениях. Отрыв происходит в результате совместного действия двух осн. факторов — торможения жидкости в пограничном слое и воздействия перепада давления. Внутри пограничного слоя скорость жидкости или газа уменьшается и её кинетич. энергии оказывается недостаточно для преодоления возрастающего давления. В результате вблизи поверхности возникает область возвратного течения, пограничный слой утолщается и, наконец, осн. поток отрывается от стенки (рис. 6) (см. Отрывное течение).
Способность течения в пограничном слое противостоять повышению давления имеет важное значение в случае падения на тело ударных волн, или скачков уплотнения. Существует критич. значение отношения давлений в скачке р₂/p₁(т. н. критич. перепад, где р₂ — давление за, а р₁ — перед скачком уплотнения), при к-ром взаимодействие скачка уплотнения с пограничным слоем приводит к отрыву последнего.

Рис. 6. Отрыв пограничного слоя при наличии положительного градиента давления.

Величина критич. перепада давления (р₂/р₁)_кр зависит от режима течения в пограничном слое, числа Маха, а для ламинарного пограничного слоя и от числа Рейнольдса. При воздействии достаточно сильного скачка уплотнения на тело пограничный слой отрывается и возникает конфигурация т. н.-скачка, у к-рого наклон передней «ножки» формируется таким образом, чтобы перепад давления на ней был равен критическому (рис. 7).