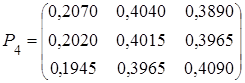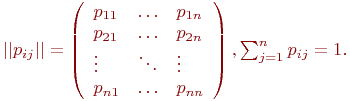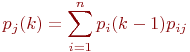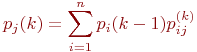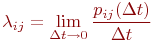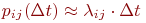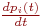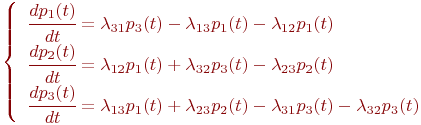Предельные вероятности состояний
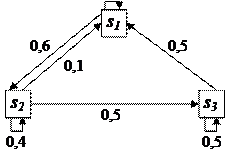
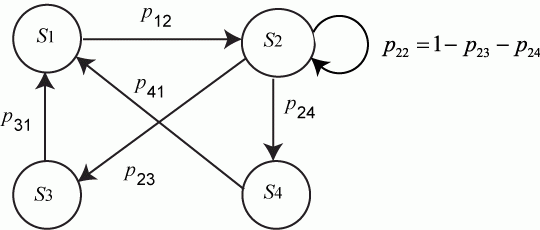
Рассмотрим математическое описание марковского процесса с дискретными состояниями и непрерывным временем* на примере случайного процесса из примера 1, граф которого изображен на рис. 1. Будем полагать, что все переходы системы из состояния в происходят под воздействием простейших потоков событий с интенсивностями ; так, переход системы из состояния в будет происходить под воздействием потока отказов первого узла, а обратный переход из состояния в — под воздействием потока «окончаний ремонтов» первого узла и т.п.
Граф состояний системы с проставленными у стрелок интенсивностями будем называть размеченным (см. рис. 1). Рассматриваемая система имеет четыре возможных состояния: .
Вероятностью i-го состояния называется вероятность того, что в момент система будет находиться в состоянии . Очевидно, что для любого момента сумма вероятностей всех состояний равна единице:
Рассмотрим систему в момент и, задав малый промежуток , найдем вероятность того, что система в момент будет находиться в состоянии . Это достигается разными способами.
1. Система в момент с вероятностью находилась в состоянии , а за время не вышла из него.
Вывести систему из этого состояния (см. граф на рис. 1) можно суммарным простейшим потоком с интенсивностью , т.е. в соответствии с формулой (7), с вероятностью, приближенно равной . А вероятность того, что система не выйдет из состояния , равна . Вероятность того, что система будет находиться в состоянии по первому способу (т.е. того, что находилась в состоянии и не выйдет из него за время ), равна по теореме умножения вероятностей:
2. Система в момент с вероятностями (или ) находилась в состоянии или и за время перешла в состояние .
Потоком интенсивностью (или — с- рис. 1) система перейдет в состояние с вероятностью, приближенно равной (или ). Вероятность того, что система будет находиться в состоянии по этому способу, равна (или ).
Применяя теорему сложения вероятностей, получим
Переходя к пределу при (приближенные равенства, связанные с применением формулы (7), перейдут в точные), получим в левой части уравнения производную (обозначим ее для простоты ):
Получили дифференциальное уравнение первого порядка, т.е. уравнение, содержащее как саму неизвестную функцию, так и ее производную первого порядка.
Рассуждая аналогично для других состояний системы , можно получить систему дифференциальных уравнений Колмогорова для вероятностей состояний:
Сформулируем правило составления уравнений Колмогорова . В левой части каждого из них стоит производная вероятности i-го состояния. В правой части — сумма произведений вероятностей всех состояний (из которых идут стрелки в данное состояние) на интенсивности соответствующих потоков событий, минус суммарная интенсивность всех потоков, выводящих систему из данного состояния, умноженная на вероятность данного (i-го состояния).
В системе (9) независимых уравнений на единицу меньше общего числа уравнений. Поэтому для решения системы необходимо добавить уравнение (8).
Особенность решения дифференциальных уравнений вообще состоит в том, что требуется задать так называемые начальные условия, т.е. в данном случае вероятности состояний системы в начальный момент . Так, например, систему уравнений (9) естественно решать при условии, что в начальный момент оба узла исправны и система находилась в состоянии , т.е. при начальных условиях .
Уравнения Колмогорова дают возможность найти все вероятности состояний как функции времени . Особый интерес представляют вероятности системы в предельном стационарном режиме , т.е. при , которые называются предельными (или финальными) вероятностями состояний.
В теории случайных процессов доказывается, что если число состояний системы конечно и из каждого из них можно (за конечное число шагов) перейти в любое другое состояние, то предельные вероятности существуют.
Предельная вероятность состояния имеет четкий смысл: она показывает среднее относительное время пребывания системы в этом состоянии . Например, если предельная вероятность состояния , т.е. , то это означает, что в среднем половину времени система находится в состоянии .
Так как предельные вероятности постоянны, то, заменяя в уравнениях Колмогорова их производные нулевыми значениями, получим систему линейных алгебраических уравнений, описывающих стационарный режим. Для системы с графом состояний, изображенном на рис. 1), такая система уравнений имеет вид:
Систему (10) можно составить непосредственно по размеченному графу состояний, если руководствоваться правилом , согласно которому слева в уравнениях стоит предельная вероятность данного состояния , умноженная на суммарную интенсивность всех потоков, ведущих из данного состояния, а справа — сумма произведений интенсивностей всех потоков, входящих в i-е состояние, на вероятности тех состояний, из которых эти потоки исходят.
Пример 2. Найти предельные вероятности для системы из примера 1, граф состояний которой приведен на рис. 1, при
Решение. Система алгебраических уравнений, описывающих стационарный режим для данной системы, имеет вид (10) или
(Здесь мы вместо одного «лишнего» уравнения системы (10) записали нормировочное условие (8)).
Решив систему (11), получим , т.е. в предельном, стационарном режиме система в среднем 40% времени будет находиться в состоянии (оба узла исправны), 20% — в состоянии (первый узел ремонтируется, второй работает), 27% — в состоянии (второй узел ремонтируется, первый работает) и 13% времени — в состоянии (оба узла ремонтируются)
Пример 3. Найти средний чистый доход от эксплуатации в стационарном режиме системы в условиях примеров 1 и 2, если известно, что в единицу времени исправная работа первого и второго узлов приносит доход соответственно в 10 и 6 ден.ед., а их ремонт требует затрат соответственно в 4 и 2 ден.ед. Оценить экономическую эффективность имеющейся возможности уменьшения вдвое среднего времени ремонта каждого из двух узлов, если при этом придется вдвое увеличить затраты на ремонт каждого узла (в единицу времени).
Решение. Из примера 2 следует, что в среднем первый узел исправно работает долю времени, равную , а второй узел — . В то же время первый узел находится в ремонте в среднем долю времени, равную , а второй узел — . Поэтому средний чистый доход в единицу времени от эксплуатации системы, т.е. разность между доходами и затратами, равен
Уменьшение вдвое среднего времени ремонта каждого из узлов в соответствии с (6) будет означать увеличение вдвое интенсивностей потока «окончаний ремонтов» каждого узла, т.е. теперь и система линейных алгебраических уравнений (10), описывающая стационарный режим системы , вместе с нормировочным условием (8) примет вид:
Решив систему, получим .
Учитывая, что , а затраты на ремонт первого и второго узла составляют теперь соответственно 8 и 4 ден.ед., вычислим средний чистый доход в единицу времени:
Так как больше (примерно на 20%), то экономическая целесообразность ускорения ремонтов узлов очевидна.
Видео:Матрица интенсивностей. Система уравнений КолмогороваСкачать

Процесс гибели и размножения
В теории массового обслуживания широкое распространение имеет специальный класс случайных процессов — так называемый процесс гибели и размножения . Название этого процесса связано с рядом биологических задач, где он является математической моделью изменения численности биологических популяций.
Граф состояний процесса гибели и размножения имеет вид, показанный на рис. 4.
Рассмотрим упорядоченное множество состояний системы . Переходы могут осуществляться из любого состояния только в состояния с соседними номерами, т.е. из состояния возможны переходы только либо в состояние , либо в состояние .
Предположим, что все потоки событий, переводящие систему по стрелкам графа, простейшие с соответствующими интенсивностями или .
По графу, представленному на рис. 4, составим и решим алгебраические уравнения для предельных вероятностей состояний (их существование вытекает из возможности перехода из каждого состояния в каждое другое и конечности числа состояний).
В соответствии с правилом составления таких уравнений (см. 13) получим: для состояния
для состояния имеем , которое с учетом (12) приводится к виду
Аналогично, записывая уравнения для предельных вероятностей других состояний, можно получить следующую систему уравнений:
к которой добавляется нормировочное условие
При анализе численности популяций считают, что состояние соответствует численности популяции, равной , и переход системы из состояния в состояние происходит при рождении одного члена популяции, а переход в состояние — при гибели одного члена популяции.
Решая систему (14), (15), можно получить
Легко заметить, что в формулах (17) для коэффициенты при есть слагаемые, стоящие после единицы в формуле (16). Числители этих коэффициентов представляют произведение всех интенсивностей, стоящих у стрелок, ведущих слева направо до данного состояния , а знаменатели — произведение всех интенсивностей, стоящих у стрелок, ведущих справа налево до состояния .
Пример 4. Процесс гибели и размножения представлен графом (рис. 5). Найти предельные вероятности состояний.
Видео:Предельные вероятности состоянийСкачать

Стационарный режим для цепи Маркова
В ряде задач практики нас интересует так называемый установившийся или стационарный режим работы системы, который в ней устанавливается, когда от начала процесса прошло достаточно большое время. Например, процесс изменения напряжения в сети питания технического устройства, пройдя сразу после включения через ряд колебаний, по прошествии времени устанавливается. Аналогично этому и в некоторых случайных процессах по прошествии достаточно большого времени устанавливается стационарный режим, во время которого состояния системы хотя и меняются случайным образом, но их вероятности pi(t) (i = 1, 2, …) остаются постоянными. Обозначим эти постоянные вероятности pi:
pi = 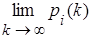
Вероятности pi (i = 1, 2, …), если они существуют, называются финальными (предельными) вероятностями состояний. Финальную вероятность pi можно понимать как среднюю долю времени, которую в стационарном режиме проводит система S в состоянии si.
Например, если рассматривать некое техническое устройство в двух состояниях: s1 – исправно, s2 – неисправно
 |
то имеет место следующая динамика изменения вероятностей при начальных условиях р1(0) = 0, р2(0) = 0: р1(1) = 0,7, р1(2) = 0,61, р1(3) = 0,583, р1(4) = 0,5749 (доказать самим). Ниже мы покажем, что в этом случае р1 = 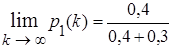
Можно убедиться, что в этом примере финальные вероятности не зависят от начальных условий.
Сформулируем условия существования стационарного режима для системы S с конечным числом состояний n, в котором протекает марковский случайный процесс с дискретным состоянием и дискретным временем (цепь Маркова):
1. Множество всех состояний W системы S должно быть эргодическим.
2. Цепь Маркова должна быть однородной, т.е. pij(k) = pij.
3. Цепь Маркова должна быть «достаточно хорошо перемешиваемой» (не должна быть «циклической»).
Цепи Маркова, отвечающие этим условиям, будем называть эргодическими цепями Маркова.
Первое условие означает, что из любого состояния 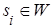

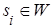
Если все условия стационарного режима выполняются, то финальные вероятности не зависят от того, каково было состояние системы S в момент времени t0 = 0 или каковым было распределение вероятностей в момент времени t0 = 0.
Условия наличия стационарного режима можно представить наглядно в виде размеченного графа состояний. Первое условие состоит в том, что размеченный граф системы должен иметь все состояния и все группы состояний транзитивными. Второе условие: все переходные вероятности должны быть постоянными: pij(k) = pij. Третье условие состоит в том, что необходимо, чтобы моменты попадания в отдельные состояния или группы состояний не образовывали циклов.
Например граф следующего вида
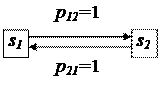 |
соответствует первым двум условиям, но третье условие не выполняется.
Если р1(0) = 1, то при k нечетном р1(k) = 0, р2(k) = 1, а при k четном р1(k)= 1, р2(k) = 0. Матрица переходных вероятностей для этого графа имеет вид 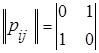
В общем случае не будет стационарного режима и у системы, размеченный граф состояний которой имеет следующий вид
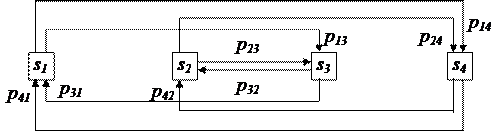 |
несмотря на то, что первые два условия выполняются. Действительно, если, например р1(0) + р2(0) = 1, то при k нечетном система будет находиться в подмножестве состояний <s3, s4>, а при k четном – в подмножестве состояний<s1, s2>:
Матрица переходных вероятностей, соответствующая данному графу, имеет вид
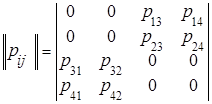
При этом выполняется условие: все переходные вероятности, указанные на размеченном графе, отличны от нуля и единицы.
В дальнейшем при рассмотрении стационарных режимов предполагается, что третье условие выполняется.
Будем считать, что условия существования финальных вероятностей выполнены и пределы
pi = 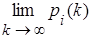
существуют и не зависят от начальных условий. Покажем, как найти эти вероятности.
Если цепь Маркова однородна, т.е. pij(k) = pij, то для стационарного режима (достигаемого при k → ∞) вероятность pj состояния sj на (k + 1)-м шаге должна быть такой же, как на k-м:
pj(k + 1) = 
где pj уже не зависит от k. Отсюда
pj = 
Сумма в правой части последнего равенства распространяется на все значения номера состояний i, включая i = j, при этом pjj – вероятность задержки системы в состоянии j. Разделим эту сумму на две части: в первой суммирование произведем по всем значениям i, кроме i = j, а во второй будет только один член, отвечающий условию i = j. Тогда
pj = 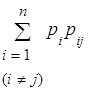
откуда при любом j получаем для pj линейное алгебраическое уравнение вида
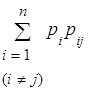
Придавая в этой формуле индексу j значения 1, 2, …, n, получим для n финальных вероятностей p1, p2, …, pn систему n линейных однородных алгебраических уравнений
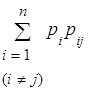
Как известно из алгебры, такая система уравнений имеет бесконечное множество решений. В рассматриваемом случае решение становится единственным, если добавить к системе (1) нормировочное условие

взамен которого можно устранить из системы (1) любое, например, первое. Получим систему уже n неоднородных линейных уравнений с n неизвестными
|
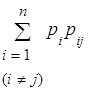

В курсе линейной алгебры доказывается, что такая система имеет единственное решение, т.е. однозначно определяет финальные вероятности p1, p2, …, pn, дающие в сумме единицу.
Таким образом, можно сформулировать следующую теорему.
Теорема. Если существуют финальные вероятности, то финальный вектор (р1, р2, …, рn) можно найти из уравнения
где Р – матрица переходных вероятностей.
При составлении системы линейных уравнений (2) для финальных вероятностей p1, p2, …, pn удобно пользоваться понятием «потока вероятностей». Назовем произведение pipij потоком вероятности, переводящим систему S из состояния si в состояние sj. Полная вероятность перехода системы S в состояние sj откуда бы то ни было равна сумме всех потоков вероятности, переводящих систему в это состояние, т.е. вероятность прийти в состояние sj откуда бы то ни было равна

Аналогично, сумма всех потоков вероятности, выводящих систему из состояния sj куда бы то ни было, равна
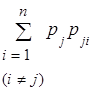

Очевидно, что в стационарном режиме вероятность войти в любое состояние должна быть равна вероятности из него выйти (иначе режим не был бы стационарным). Уравнения для финальных вероятностей можно записывать, исходя из следующего правила: для стационарного режима суммарный поток вероятности, переводящий систему S в состояние sj из других состояний, равен суммарному потоку вероятности, выводящему систему из состояния sj:
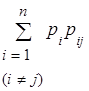

Условие (3) назовем балансовым условием для состояния sj. К этим условиям надо добавить нормировочное условие

отбросив одно любое уравнение из (3). Полученная система решается любым из известных методов из линейной алгебры.
Решение типовых задач
1. Совокупность семей некоторого региона можно разделить на три группы
1) Семьи, не имеющие автомобиля и не собирающиеся его покупать;
2) Семьи, не имеющие автомобиля, но намеревающиеся его приобрести;
3)Семьи, имеющие автомобиль.
Проведенное статистическое исследование показало, что матрица перехода за интервал один год имеет вид
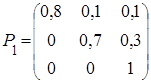
В этой матрице элемент р33 = 1 означает вероятность того, что семья, имеющая автомобиль через год также будет его иметь, а , например, элемент р23 = 0,3 – вероятность того, что семья, не имевшая автомобиля, не решившая его приобрести, осуществит свое намерение в следующем году, и т.д.
Найти вероятности того, что
а) Семья, не имевшая автомобиля и не собиравшаяся его приобрести, будет в такой же ситуации через два года.
Б) Семья, не имевшая автомобиля, но намеревающаяся его приобрести, будет иметь автомобиль через 2 года.
Решение. Найдем матрицу перехода Р2 через два года
Р2 = 
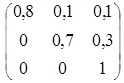
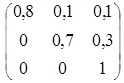
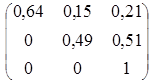
Отсюда искомые в а) и б) вероятности равны соответственно р11 = 0,64 и р23 = 0,51. ►

 |
Решение. Определим тип процесса. Так как множество состояний, в которых может находиться система, конечно – три состояния – то случайный процесс является дискретным.
С определенной долей погрешности можно предположить, что вероятность пребывания банка в одном из своих состояний в будущем не зависит от его состояний в прошлом, и зависит в существенном только от его состояния в настоящем. Поэтому случайный процесс можно считать марковским. В силу условий примера банк может переходить из состояния в состояние только в заранее определенные моменты времени — в начале каждого квартала. Следовательно, случайный процесс есть процесс с дискретным временем.
Так как зависимостью переходных вероятностей можно пренебречь, то рассматриваемый процесс будет однородным.
Следовательно, рассматриваемый случайный процесс является однородной цепью Маркова.
По размеченному графу состояний найдем значения вероятностей задержек.
Теперь составим матрицу переходных вероятностей за один квартал

Так как в конце предшествующего года процентная ставка составляла 3%, то можно считать, что в начальный момент времени система находилась в состоянии s2. Поэтому начальное распределение вероятностей имеет вид р1(0)=0, р2(0) = 1, р3 (0) = 0.
Вероятность состояний банка в конце года, т.е. по прошествии четырех кварталов, находим по формуле Р4 = Р1 4 , следовательно,
Чтобы найти вероятности состояний в конце года, надо вектор начальных состояний умножить на получившуюся матрицу:
= (0; 1; 0) ∙ 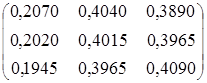
Итак, р1(4) = 0,2020, р2(4) = 0,4015, р3 (4) = 0,3965, т.е. в конце года вероятнее всего процентная ставка останется такой же, как и в предшествующем году, т.е. 3%.►

Спрогнозируйте, какая ставка будет к концу 2014 года, если в 2010 году процентная ставка была 5%, а размеченный граф состояний выглядит следующим образом:
 |
Ответ. Через 4 года процентные ставки 5%, 8% и 11% будут соответственно с вероятностями 0,2261; 0,4998 и 0,2741.Следовательно, в 2014 году ставка вероятнее всего будет 8%.

Р(1) = 
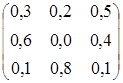
Р(3) = 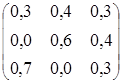

В конце предшествующего года процентная ставка была 4%. Какой будет процентная ставка в конце этого года? Изобразить размеченные графы состояний системы для каждого квартала.
Решение. Изобразим размеченные графы состояний системы, указывая только те стрелки, переходные состояния которых отличны от нуля.
|
Шаг k = 1.
 |
|
Шаг k = 2.
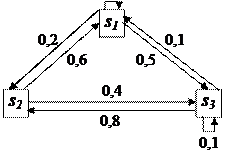 |
|
Шаг k =3.
|
Шаг k =4.
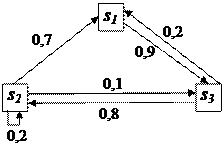
По условию вероятности состояний системы в начальный момент времени
Р(1)∙Р(2) = 
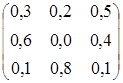
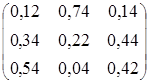
Р(1)∙Р(2)∙Р(3) = 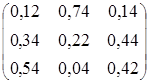
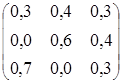
Р(1)∙Р(2)∙Р(3)∙Р(4) = 

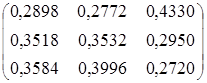
= (0, 0, 1)∙ 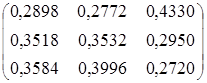
Таким образом p1(4) = 0,3584, p2(4) = 0,3696, p3(4) = 0,2720, и наиболее вероятной процентной ставкой в конце года будет 3%.►
 |
5. 



 |
и задана матрица переходных состояний 
В начальный момент времени (t0 = 0) система находится в состоянии s1. Составить для системы размеченный граф состояний Найти распределение вероятностей состояний системы для первых четырех шагов (k = 1, 2, 3, 4); убедиться, что вероятность поглощающего состояния p4(k) с увеличением k растет.
Решение. Составим для системы размеченный граф состояний.
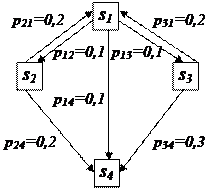 |
Так как в начальный момент времени (t0 = 0) система находится в состоянии s1, то p1(0) = 1, p2(0) = p3(0) = p4(0) = 0. По формуле
pj(k) = 
Снова применяя формулу, находим вероятности состояний на втором шаге
p1(4) = 0,421·0,7 + 0,131·0,2 + 0,113·0,2 = 0,3435;
Мы убедились в том, что с возрастанием k вероятность поглощающего состояния p4(k) растет, тогда как вероятность p1(k) состояния s1 растет. ►
6. Рассмотрим систему S – станок с числовым программным управлением, который может быть в следующих состояниях:
s1 – исправен и работает;
s2 – неисправен и неисправность не обнаружена;
s3 – неисправен, проводится средний ремонт;
s4 – не работает, находится на профилактике;
s5 – неисправен, проводится капитальный ремонт.
Размеченный граф состояний имеет следующий вид
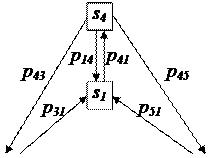 |
|
 |
Решение. Рассмотрим состояние s5 на графе. В это состояние направлено две стрелки, следовательно, в левой части уравнения (3) для j = 5 (состояние s5) будет два слагаемых. Из этого состояния выходит одна стрелка, следовательно, в правой части уравнения (3) для j = 5 будет одно слагаемое. Получаем первое уравнение
Аналогично запишем еще три уравнения:
В качестве пятого уравнения возьмем нормировочное условие
Перепишем полученную систему уравнений в таком виде:
Решим эту систему уравнений. Из 2) находим
Подставляя соответствующие значения вероятностей, получим
а2 = 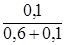

а4 = 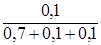
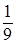
а3 = 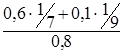

а5 = 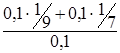
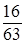
Подставляя полученные значения в равенство 5) получаем уравнение
р1 + 

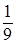
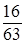
р1 = 
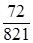
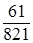
p4 = а4р1 = 
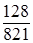
Обратим внимание, что для решения этого примера нам потребовались только те вероятности, которые приведены на размеченном графе, и не потребовались вероятности задержки р11, р22, р33, р44, р55.

s1 – один блок неисправен, остальные два работают,
s2 – два блока исправны, один работает,
s3 – все три блока неисправны.
Полагая r = 0,2, q = 0,3, построить размеченный граф состояний ВЦ и найти финальные вероятности.
Решение. Размеченный граф состояний имеет следующий вид
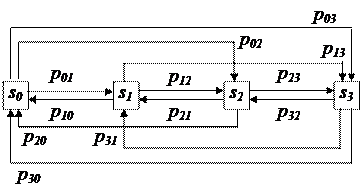 |
Вычислим переходные вероятности pij.
Чтобы система перешла из состояния s0 в состояние s1, нужно, чтобы один из блоков на время t вышла из строя. Эта вероятность, согласно биномиальному распределению, равна р01 = 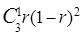
р02 = 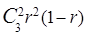
Чтобы система из состояния s1 перешла в состояние s0, нужно, чтобы неисправный блок за время t был отремонтирован, а другие два исправных блока не вышли из строя: р10 = q(1 – r) 2 . Аналогично находим
Рассуждая таким же способом, определяем
р33 = (1 – q) 3 , р32 = 
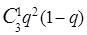
Теперь при r = 0,2 и q = 0,3 имеем
Для нашего примера система уравнений
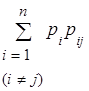

с учетом нормировочного условия 
Решая полученную систему линейных неоднородных уравнений одним из известных методов линейной алгебры, получим

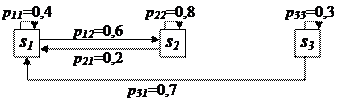 |
Найти финальные вероятности.
Решение. Матрица переходных вероятностей имеет вид
Р = 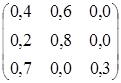
Тогда вектор финальных вероятностей
(р1, р2, р3) = (р1, р2, р3)∙Р = (р1, р2, р3)∙ 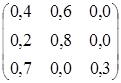
Произведя умножение в правой части этого равенства, получим
Отсюда получаем следующую систему линейных уравнений
Из первого уравнения
р1 = 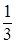
Итак, (р1 = 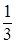
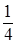
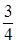
Окончательно вектор финальных вероятностей (р1, р2, р3) = 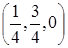

Решение. В качестве системы S будем рассматривать рынок ценных бумаг. Тогда система S может находиться только в двух состояниях: s1 – падение цен, и s2 – возрастание цен, следовательно, процесс, протекающий в системе S, является дискретным.
Предстоящее состояние, в которое перейдет система S, зависит (в существенном) от состояния, в котором она находится в настоящий момент времени, поэтому процесс является марковским.
Будем предполагать, что моменты времени t1, t2, t3, … настолько близки друг к другу, что между ними система S не изменяет своего состояния и, следовательно, процесс с определенной погрешностью можно считать процессом с дискретным временем.
Условные вероятности 0,65 и 0,6, данные в условии, являются, очевидно, вероятностями р12 и р21. Тогда
Размеченный граф состояний будет иметь следующий вид
 |
Матрица переходных вероятностей
Р = 
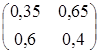
Вектор финальных вероятностей ищем из уравнения
(р1, р2) = (р1, р2)∙Р = (р1, р2)∙ 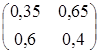
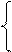
|
р1 = 0,35р1 + 0,6р2; 0,65р1 – 0,6р2 = 0;
Уравнения полученной системы пропорциональны, поэтому одно из них (например, второе) можно отбросить, заменяя его нормировочным уравнением, т.е. получая систему
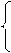
Решая эту систему, находим вектор финальных вероятностей
Таким образом, при достаточно длительном функционировании рынка ценных бумаг финальные вероятности падения и роста цен равны соответственно 0,48 и 0,52. При этом они не зависят от начального состояния рынка.►
10. Компания по прокату автомобилей выдает автомобили напрокат в трех аэропортах А, В и С. Клиенты возвращают автомобили в эти аэропорты в соответствии с вероятностями, указанными в следующей таблице
| Откуда | Куда | ||
| А | В | С | |
| А | 0,75 | 0,25 | |
| В | 0,25 | 0,75 | |
| С | 0,25 | 0,25 | 0,5 |
Компания планирует построить ремонтную станцию в одном из этих трех аэропортов. В каком из них это целесообразно сделать и почему?
Решение. Каждый автомобиль можно рассматривать в качестве системы S, которая может пребывать в одном из следующих трех состояний:
s1 – автомобиль находится в аэропорту А и не выдан напрокат или выдан напрокат из аэропорта А и находится у клиента;
Тогда вероятности, данные в условии задачи в таблице, являются переходными вероятностями системы S из одного из состояний s1, s2, s3 в другое.
Промежуток времени между выдачей и возвращением автомобиля не может быть сколь угодно бесконечно малым и потому моменты времени t1,t2,t3,… можно выбрать настолько близкими друг к другу, что между ними система S не изменяет своего состояния. Следовательно, процесс, протекающий в системе S, можно считать процессом с дискретным временем.
Таким образом, матрица переходных вероятностей
Р = 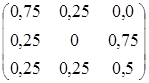
Вектор финальных вероятностей ищем из уравнения
(р1, р2, р3) = (р1, р2, р3)∙Р = (р1, р2, р3)∙ 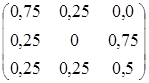
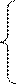

Заменяя, например, второе уравнение системы нормировочным уравнение, получим
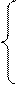
Решая последнюю систему, получим вектор финальных вероятностей (р1,р2, р3) = (0,5, 0,2, 0,3). Таким образом, ремонтную станцию целесообразно строить в аэропорту А, т.к. финальная вероятность возврата в этот аэропорт наибольшая.►
Видео:Стационарное распределение вероятностей состоянийСкачать

Марковские случайные процессы. Уравнения Колмогорова для вероятностей состояний.
Наиболее полное исследование процесса функционирования систем получается, если известны явные математические зависимости, связывающие искомые показатели с начальными условиями, параметрами и переменными исследуемой системы. Для многих современных систем, являющихся объектами моделирования, такие математические зависимости отсутствуют или малопригодны, и следует применять другое моделирование, как правило, имитационное.
Большой класс случайных процессов составляют процессы без последействия, которые в математике называют марковскими процессами в честь Андрея Андреевича Маркова — старшего (1856 — 1922), выдающегося русского математика, разработавшего основы теории таких процессов.
Случайный процесс называется марковским, если вероятность перехода системы в новое состояние зависит только от состояния системы в настоящий момент и не зависит от того, когда и каким образом система перешла в это состояние.
Практически любой случайный процесс является марковским или может быть сведен к марковскому. В последнем случае достаточно в понятие состояния включить всю предысторию смен состояний системы.
Марковские процессы делятся на два класса:
· дискретные марковские процессы (марковские цепи);
· непрерывные марковские процессы.
Дискретной марковской цепьюназывается случайный процесс, при котором смена дискретных состояний происходит в определенные моменты времени.
Непрерывным марковским процессомназывается случайный процесс, при котором смена дискретных состояний происходит в случайные моменты времени.
Рассмотрим ситуацию, когда моделируемый процесс обладает следующими особенностями.
Система 
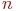
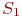
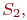
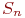
Смена состояний происходит, будем считать, мгновенно и в строго определенные моменты времени 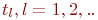
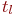
Известны вероятности перехода 

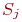
Цель моделирования: определить вероятности состояний системы после 
Обозначим эти вероятности 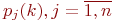

Если в системе отсутствует последействие, то есть вероятности 

Марковская цепь называется однородной, если переходные вероятности 
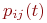
Значения 
Значения 
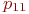
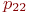
Не указываются также нулевые вероятности переходов. Например, на рис. это вероятности 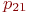
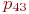
Математической моделью нахождения вероятностей состояний однородной марковской цепи является рекуррентная зависимость
где 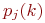
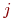

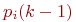
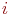

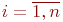
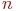

Рис.Размеченный граф состояний системы
Для неоднородной марковской цепи вероятности состояний системы находятся по формуле:
где 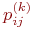

Сформулируем методику моделирования по схеме дискретных марковских процессов (марковских цепей).
1. Зафиксировать исследуемое свойство системы.
Определение свойства зависит от цели исследования. Например, если исследуется объект с целью получения характеристик надежности, то в качестве свойства следует выбрать исправность. Если исследуется загрузка системы, то — занятость. Если состояния объектов, то — поражен или непоражен.
2. Определить конечное число возможных состояний системы и убедиться в правомерности моделирования по схеме дискретных марковских процессов.
3. Составить и разметить граф состояний.
4. Определить начальное состояние.
5. По рекуррентной зависимости определить искомые вероятности.
В рамках изложенной методики моделирования исчерпывающей характеристикой поведения системы является совокупность вероятностей 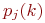
При моделировании состояния систем с непрерывными марковскими процессами мы уже не можем воспользоваться переходными вероятностями 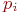

Поэтому вместо переходных вероятностей вводятся в рассмотрение плотности вероятностей переходов 
где 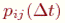


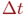
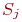
С точностью до бесконечно малых второго порядка из приведенной формулы можно представить:
Непрерывный марковский процесс называется однородным,если плотности вероятностей переходов 

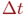
Целью моделирования,как и в случае дискретных процессов, является определение вероятностей состояний системы 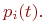
Сформулируем методику моделирования по схеме непрерывных марковских процессов.
1. Определить состояния системы и плотности вероятностей переходов 
2. Составить и разметить граф состояний.
3. Составить систему дифференциальных уравнений Колмогорова. Число уравнений в системе равно числу состояний. Каждое уравнение формируется следующим образом.
4. B левой части уравнения записывается производная вероятности 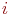
5. В правой части записывается алгебраическая сумма произведений 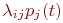
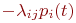
6. Определить начальные условия и решить систему дифференциальных уравнений.
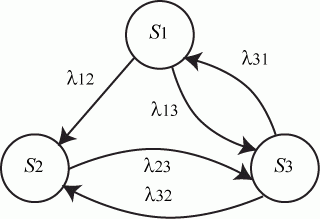
Пример. Составить систему дифференциальных уравнений Колмогорова для нахождения вероятностей состояний системы, размеченный граф состояний которой представлен на рисунке.
Рис. Размеченный граф состояний
Очевидно, 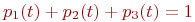
Поэтому любое из первых трех уравнений можно исключить, как линейно зависимое.
Для решения уравнений Колмогорова необходимо задать начальные условия. Для рассмотренного примера можно задать такие начальные условия: 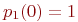
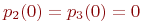
Дата добавления: 2015-04-03 ; просмотров: 7833 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
🎦 Видео
Цепи МарковаСкачать

Стационарное распределение вероятностей состоянийСкачать

Волновая функция (видео 5) | Квантовая физика | ФизикаСкачать

Лекция 12. Стационарные состояния.Уравнение Шредигера для стационарных состояний.Скачать

Цепи Маркова (видео 12) | Теория информации | ПрограммированиеСкачать

Как летает самолет? Закон Бернулли - Основы авиации #2Скачать

Многоканальная СМО с отказамиСкачать

Урок 455. Уравнение ШрёдингераСкачать

Уравнение Шредингера Стационарные состоянияСкачать

Решение системы уравнений методом ГауссаСкачать

7 класс, 39 урок, Метод алгебраического сложенияСкачать

04 Эргодические цепи МарковаСкачать

Стационарные состояния.Квантовая физикаСкачать

Закон БернуллиСкачать

Энергетические уровни атома (видео 6) | Квантовая физика | ФизикаСкачать

Пример анализа состояний системСкачать

Авакянц Л. П. - Введение в квантовую физику - Нестационарные состоянияСкачать