Система уравнений для определения реакций в опоре защемленной балки

Видео:Определение реакций опор в жесткой заделке консольной балкиСкачать

Определение реакций опор балки – решение задачи

Видео:Определение опорных реакций балки. Сопромат для чайников ;)Скачать

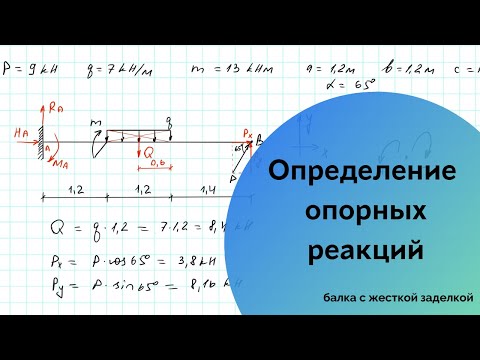
Как определить реакции опор балки

Видео:Определение реакций опор в балке. Сопромат.Скачать

Пример решения задачи на определение реакций опор балки

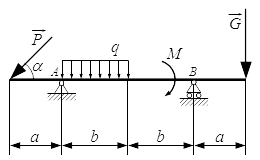
Жесткая балка, линейные размеры которой указаны на рисунке 1, закреплена в точках А и В. На балку действуют пара сил с моментом М, равномерно распределенная нагрузка интенсивностью q и две силы P и G, место приложения которых показано на рисунке.
Определить реакции опор балки в точках A и B, вызываемые указанными нагрузками.

Дано:
P = 20,2 Н ; G = 22,6 Н ; q = 2 Н/м ; M = 42,8 Н·м ; a = 1,3 м ; b = 3,9 м ; α = 45° ;

Решение задачи

Проводим оси x и y системы координат. Начало системы координат поместим в точку A . Ось x направим горизонтально, вдоль балки. Ось y – вертикально. Ось z перпендикулярна плоскости рисунка и направлена на нас. На рисунке она не указана.

Силы, действующие на балку.

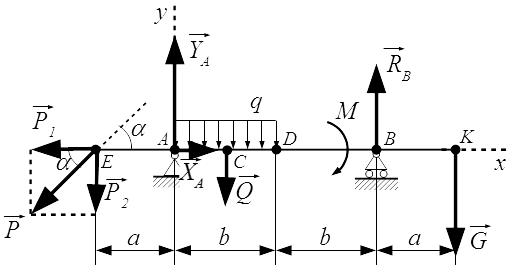
Отбрасываем опоры и заменяем их силами реакций.
В шарнире A , разложим силу реакции на составляющие и вдоль осей координат.
Реакция , в подвижной опоре на катках, направлена вертикально. Предполагаемые направления реакций опор выбираем по своему усмотрению, наугад. Если ошибемся с направлением реакции, то получим отрицательное значение, что будет говорить о том, что соответствующая сила реакции направлена в противоположную сторону.

Заменим равномерно распределенную нагрузку q равнодействующей . Абсолютное значение равнодействующей равно площади эпюры:
Н .
Точка приложения равнодействующей находится в центре тяжести эпюры. Поскольку эпюра представляет собой прямоугольник, то ее центр тяжести находится в точке C – посередине отрезка AD :
AC = CD = b/2 = 1,95 м .

Уравнения равновесия для сил

Определяем проекции сил на оси координат.

Разложим силу на составляющие вдоль координатных осей:
.
Абсолютные значения составляющих:
.
Вектор параллелен оси x и направлен в противоположную от нее сторону. Вектор параллелен оси y и также направлен в противоположную сторону. Поэтому проекции силы на оси координат имеют следующие значения:
.

Остальные силы параллельны осям координат. Поэтому они имеют следующие проекции:
;
;
;
;
.

Составляем уравнения равновесия для сил.
Сумма проекций всех сил на ось x равна нулю:
;
;
;
(П1) .

Сумма проекций всех сил на ось y равна нулю:
;
;
;
(П2) .

Уравнения равновесия для моментов

Итак, мы уже составили два уравнения для сил: (П1) и (П2). Но в них есть три неизвестные величины: , и . Чтобы их определить, нам нужно составить еще одно уравнение.

Составим уравнение равновесия для моментов сил. Для этого нам нужно выбрать ось, относительно которой мы будем вычислять моменты. В качестве такой оси возьмем ось, проходящую через точку A , перпендикулярно плоскости рисунка. За положительное направление выберем то, которое направлено на нас. Тогда, по правилу правого винта, положительным направлением закручивания будет направление против часовой стрелки.

Находим моменты сил относительно выбранной оси.
Силы , и пересекают ось. Поэтому их моменты равны нулю:
; ; .

Сила перпендикулярна плечу AB . Ее момент:
.
Поскольку, относительно оси A , сила направлена против часовой стрелки, то ее момент положительный.

Сила перпендикулярна плечу AK . Поскольку, относительно оси A , эта сила направлена по часовой стрелки, то ее момент имеет отрицательное значение:
.

Аналогичным способом находим моменты остальных сил:
;
.
Момент от пары сил M не зависит от точек приложения сил, входящих в пару:
.

Составляем уравнение равновесия. Сумма моментов сил относительно оси A равна нулю:
;

;
;
(П3) .

Решение уравнений равновесия

Итак, для трех неизвестных величин, мы получили три уравнения:
(П1) .
(П2) .
(П3) .

Решаем эти уравнения. Вычисляем расстояния.
м;
м;
м;
м.

Из уравнения (П1) находим:
Н.
Из уравнения (П3) находим:

Н.
Из уравнения (П2) имеем:
Н.
Абсолютное значение реакции опоры в точке A :
Н.

Проверка правильности решения

Чтобы проверить, правильно ли мы определили реакции опор балки, найдем сумму моментов сил относительно другой оси. Если мы нашли реакции правильно, то она должна равняться нулю.

Возьмем ось, проходящую через точку E . Вычисляем сумму моментов сил относительно этой оси:

.
Найдем погрешность вычисления суммы моментов. Найденные силы мы округлили до двух знаков после запятой. То есть погрешность определения реакций опор составляет 0,01 Н . Расстояния, по порядку величины, примерно равны 10 м. Тогда погрешность вычисления суммы моментов составляет около 10·0,01 = 0,1 Нм . Мы получили значение -0,03 Нм . Эта величина отличается от нуля не более, чем на величину погрешности. То есть, с учетом погрешности вычислений, сумма моментов относительно другой оси равна нулю. Значит решение правильное, силы реакций найдены верно.

Второй способ решения

Первым способом мы составили два уравнения для сил и одно – для моментов. Задачу можно решить другим способом, составив два уравнения для моментов и одно для сил.

Воспользуемся тем, что сумма моментов сил равна нулю относительно любой оси. Возьмем вторую ось, которая проходит через точку B перпендикулярно плоскости рисунка. Сумма моментов сил относительно этой равна нулю:
.
Вычисляем моменты сил относительно оси B .
; ; ;
;
;
;
;
.

Сумма моментов сил относительно оси B равна нулю:
;

;
;
(П4) ;

Итак, вторым способом, мы также имеем три уравнения:
(П1) .
(П3) ;
(П4) .

Здесь каждое уравнение содержит только одну неизвестную величину. Реакции и определяются из тех же уравнений, что и ранее. Находим силу из уравнения (П4):

Н.

Значение реакции совпало со значением, полученным первым способом из уравнения (П2).

Автор: Олег Одинцов . Опубликовано: 14-10-2017 Изменено: 28-12-2021

Видео:Определение реакций опор простой рамыСкачать

Методическая разработка по технической механике на тему: «Определение опорных реакций балок»

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Рабочие листы и материалы для учителей и воспитателей

Более 300 дидактических материалов для школьного и домашнего обучения

государственное автономное профессиональное образовательное учреждение

Челябинской области «Политехнический колледж»

ОП 07 Техническая механика

Для специальности « 22.02.06 Сварочное производство»

Тема 1.1 Основы статики

Урок 15-16 « Определение опорных реакций балок»

Тема: « Определение опорных реакций балок»

Цель занятия: з акрепить теоретические знания и умения определять реакции в опорах балочных систем

Краткие теоретические сведения

Очень часто в машинах и конструкциях встречаются тела удлиненной формы, называемые балками (или балочными системами). Балки в основном предназначены для восприятия поперечных нагрузок. Балки имеют специальные опорные устройства для сопряжения их с другими элементами и передачи на них усилий.

По способу приложения нагрузки делятся на:

сосредоточенные – если реально передача нагрузки происходит на пренебрежимо малой площадке (в точке);

распределенные – если нагрузка распределена по значительной площадке или ли­нии (давление воды на плотину, давление снега на крышу и т.п.) .

В задачах статики для абсолютно твердых тел распределен­ную нагрузку можно заменить равнодействующей сосредоточенной силой (рис. 1).

q — интенсивность на­грузки;

I — длина стержня;

G = ql — равнодей­ствующая распределенной нагрузки.

Опора не допускает перемещений и поворотов. Заделку заменя­ют двумя составляющими силы Rax и и парой с моментом Mr .

Для определения этих неизвестных удобно использовать систему уравнений в виде

Каждое уравнение имеет одну неиз­вестную величину и решается без подста­новок.

Для контроля правильности решений используют дополни­тельное уравнение моментов относительно любой точки на балке, например

Шарнирно-подвижная опора (рис. 3)

Опора допускает поворот вокруг шарнира и перемещение вдоль опорной поверхности. Реакция направлена перпендикулярно опорной поверхности.

Шарнирно-неподвижная опора (рис. 4)

Опора допускает поворот вокруг шарнира и может быть заме­нена двумя составляющими силы вдоль осей координат.

Балка на двух шарнирных опорах (рис. 5)

Не известны три силы, две из них — вертикальные, следовательно, удобнее для определения неизвестных использовать систему уравнений во второй форме:

Составляются уравнения моментов относительно точек крепле­ния балки. Поскольку момент силы, проходящей через точку креп­ления, равен 0, в уравнении останется одна неизвестная сила.

Для контроля правильности решения используется дополни­тельное уравнение

Упражнения при подготовке к самостоятельной работе

1. Привести систему сил к точке В , определить главный вектор и главный момент системы сил (рис. 6). АВ = 2м; ВС = 1,5м; CD = 1м. F ₁ = 18кН; F ₂ = 10кН; F ₃ = 30кН; т = 36кН-м.

2. Система сил находится в равновесии. Определить величину момента пары т (рис. 7).

Нанести реакции в опорах балок 1 и 2 (рис. 8).

Определить величину реакции в опоре А. Приложена распре­деленная нагрузка интенсивностью q = 5кН/м (рис. 9).

5. Записать систему уравнений равновесия для определения ре­акций в опоре защемленной балки.

Записать систему уравнений равновесия для определения ре­акций в опорах двухопорной балки, закрепленной на двух шарнирах.

Примеры решения задач

Пример№1 . Одноопорная (защемленная) балка нагружена со­средоточенными силами и парой сил (рис. 10). Определить реакции заделки.

В заделке может возникнуть реакция, представляемая двум: составляющими ( R _Ay , R _Ax ), и реактивный момент М _A . Наносим на схему балки возможные направления реакций.

Замечание. Если направления выбраны неверно, при расчетах получим отрицательные значения реакций. В этом случае реакции на схеме следует направить в противоположную сторону, не повторяя расчета.

В силу малой высоты считают, что все точки балки находятся на одной прямой; все три неизвестные реакции приложены в одной точке. Для решения удобно использовать систему уравнений равновесия в первой форме. Каждое уравнение будет содержать одну неизвестную.

Используем систему уравнений:

Знаки полученных реакций (+), следовательно, направления ре­акций выбраны верно.

3. Для проверки правильности решения составляем уравнение моментов относительно точки В.

Подставляем значения полученных реакций:

Решение выполнено верно.

Пример №2. Двухопорная балка с шарнирными опорами А и В нагружена сосредоточенной силой F , распределенной нагрузкой с интенсивностью q и парой сил с моментом т (рис. 11). Определить реакции опор.

Левая опора (точка А) — подвижный шарнир, здесь реакция направлена перпендикулярно опорной поверхности.

Правая опора (точка В) — неподвижный шарнир, здесь наносим две составляющие реакции вдоль осей координат. Ось Ох совмещаем с продольной осью балки.

Поскольку на схеме возникнут две неизвестные вертикальные реакции, использовать первую форму уравнений равновесия нецеле­сообразно.

Заменяем распределенную нагрузку сосредоточенной:

G = ql; G = 2*6 = 12 кН.

Сосредоточенную силу помещаем в середине пролета, далее за­дача решается с сосредоточенными силами (рис. 2б).

Наносим возможные реакции в опорах (направление произвольное).

Для решения выбираем уравнение равновесия в виде

6. Составляем уравнения моментов относительно точек крепления:

Реакция отрицательная, следовательно, R _{А y} нужно направить н противоположную сторону.

Используя уравнение проекций, получим:

R _Bx — горизонтальная реакция в опоре В.

Реакция отрицательна, следовательно, на схеме ее направление будет противоположно выбранному.

Проверка правильности решения. Для этого используем чет­вертое уравнение равновесия

Подставим полученные значения реакций. Если условие выполнено, решение верно:

-5,1 — 12 + 34,6 – 25 -0,7 = 0.

Решение выполнено верно.

Порядок выполнения работы:

Заменить распределенную нагрузку ее равнодействующей и указать точку ее приложения (если действует на балку).

Освободить балку от связей, заменив их реакциями.

Выбрать систему уравнений равновесия.

Решить уравнения равновесия.

Выполнить проверку решения.

Задания для самостоятельной работы:

Задание №1: Определить величины реакций в опоре защемлен­ной балки. Провести проверку правильности решения.

Задание №2: Определить величины реакций в шарнирных опорах балки. Провести проверку правильности решения.

1. Какую из форм уравнений равновесия целесообразно использовать при определении реакций в заделке?

2. Какую форму системы уравнений равновесия целесообразно использовать при определении реакций в опорах двухопорной балки и почему?

3. Сколько уравнений равновесия необходимо составить при параллельных внешних силах?

4. Как определить равнодействующую силу равномерно распределённой нагрузки?

5. Назовите формулу для определения момента силы относительно точки.

6. Сформулируйте правила знаков для определения моментов сил.

7. Как проверить правильность определения реакций опор балочных систем?

8. В каком случае момент силы равен 0?

Краткое описание документа:

государственное автономное профессиональное образовательное учреждение

Челябинской области «Политехнический колледж»

ОП 07 Техническая механика

Для специальности « 22.02.06 Сварочное производство»

Тема 1.1 Основы статики

Урок 15-16 « Определение опорных реакций балок»

Тема: « Определение опорных реакций балок»

Цель занятия: з акрепить теоретические знания и умения определять реакции в опорах балочных систем

Краткие теоретические сведения

Очень часто в машинах и конструкциях встречаются тела удлиненной формы, называемые балками (или балочными системами). Балки в основном предназначены для восприятия поперечных нагрузок. Балки имеют специальные опорные устройства для сопряжения их с другими элементами и передачи на них усилий.

По способу приложения нагрузки делятся на:

сосредоточенные – если реально передача нагрузки происходит на пренебрежимо малой площадке (в точке);

распределенные – если нагрузка распределена по значительной площадке или ли­нии (давление воды на плотину, давление снега на крышу и т.п.) .

В задачах статики для абсолютно твердых тел распределен­ную нагрузку можно заменить равнодействующей сосредоточенной силой (рис. 1).

q — интенсивность на­грузки;

I — длина стержня;

G = ql — равнодей­ствующая распределенной нагрузки.

Опора не допускает перемещений и поворотов. Заделку заменя­ют двумя составляющими силы Rax и и парой с моментом Mr .

Для определения этих неизвестных удобно использовать систему уравнений в виде

Каждое уравнение имеет одну неиз­вестную величину и решается без подста­новок.

Для контроля правильности решений используют дополни­тельное уравнение моментов относительно любой точки на балке, например

Шарнирно-подвижная опора (рис. 3)

Опора допускает поворот вокруг шарнира и перемещение вдоль опорной поверхности. Реакция направлена перпендикулярно опорной поверхности.

Шарнирно-неподвижная опора (рис. 4)

Опора допускает поворот вокруг шарнира и может быть заме­нена двумя составляющими силы вдоль осей координат.

Балка на двух шарнирных опорах (рис. 5)

Не известны три силы, две из них — вертикальные, следовательно, удобнее для определения неизвестных использовать систему уравнений во второй форме:

Составляются уравнения моментов относительно точек крепле­ния балки. Поскольку момент силы, проходящей через точку креп­ления, равен 0, в уравнении останется одна неизвестная сила.

Для контроля правильности решения используется дополни­тельное уравнение

Упражнения при подготовке к самостоятельной работе

1. Привести систему сил к точке В , определить главный вектор и главный момент системы сил (рис. 6). АВ = 2м; ВС = 1,5м; CD = 1м. F ₁ = 18кН; F ₂ = 10кН; F ₃ = 30кН; т = 36кН-м.

2. Система сил находится в равновесии. Определить величину момента пары т (рис. 7).

Нанести реакции в опорах балок 1 и 2 (рис. 8).

Определить величину реакции в опоре А. Приложена распре­деленная нагрузка интенсивностью q = 5кН/м (рис. 9).

5. Записать систему уравнений равновесия для определения ре­акций в опоре защемленной балки.

Записать систему уравнений равновесия для определения ре­акций в опорах двухопорной балки, закрепленной на двух шарнирах.

Примеры решения задач

Пример№1 . Одноопорная (защемленная) балка нагружена со­средоточенными силами и парой сил (рис. 10). Определить реакции заделки.

В заделке может возникнуть реакция, представляемая двум: составляющими ( R _Ay , R _Ax ), и реактивный момент М _A . Наносим на схему балки возможные направления реакций.

Замечание. Если направления выбраны неверно, при расчетах получим отрицательные значения реакций. В этом случае реакции на схеме следует направить в противоположную сторону, не повторяя расчета.

В силу малой высоты считают, что все точки балки находятся на одной прямой; все три неизвестные реакции приложены в одной точке. Для решения удобно использовать систему уравнений равновесия в первой форме. Каждое уравнение будет содержать одну неизвестную.

Используем систему уравнений:

Знаки полученных реакций (+), следовательно, направления ре­акций выбраны верно.

3. Для проверки правильности решения составляем уравнение моментов относительно точки В.

Подставляем значения полученных реакций:

Решение выполнено верно.

Пример №2. Двухопорная балка с шарнирными опорами А и В нагружена сосредоточенной силой F , распределенной нагрузкой с интенсивностью q и парой сил с моментом т (рис. 11). Определить реакции опор.

Левая опора (точка А) — подвижный шарнир, здесь реакция направлена перпендикулярно опорной поверхности.

Правая опора (точка В) — неподвижный шарнир, здесь наносим две составляющие реакции вдоль осей координат. Ось Ох совмещаем с продольной осью балки.

Поскольку на схеме возникнут две неизвестные вертикальные реакции, использовать первую форму уравнений равновесия нецеле­сообразно.

Заменяем распределенную нагрузку сосредоточенной:

G = ql; G = 2*6 = 12 кН.

Сосредоточенную силу помещаем в середине пролета, далее за­дача решается с сосредоточенными силами (рис. 2б).

Наносим возможные реакции в опорах (направление произвольное).

Для решения выбираем уравнение равновесия в виде

6. Составляем уравнения моментов относительно точек крепления:

Реакция отрицательная, следовательно, R _{А y} нужно направить н противоположную сторону.

Используя уравнение проекций, получим:

R _Bx — горизонтальная реакция в опоре В.

Реакция отрицательна, следовательно, на схеме ее направление будет противоположно выбранному.

Проверка правильности решения. Для этого используем чет­вертое уравнение равновесия

Подставим полученные значения реакций. Если условие выполнено, решение верно:

-5,1 — 12 + 34,6 – 25 -0,7 = 0.

Решение выполнено верно.

Порядок выполнения работы:

Заменить распределенную нагрузку ее равнодействующей и указать точку ее приложения (если действует на балку).

Освободить балку от связей, заменив их реакциями.

Выбрать систему уравнений равновесия.

Решить уравнения равновесия.

Выполнить проверку решения.

Задания для самостоятельной работы:

Задание №1: Определить величины реакций в опоре защемлен­ной балки. Провести проверку правильности решения.

Задание №2: Определить величины реакций в шарнирных опорах балки. Провести проверку правильности решения.

1. Какую из форм уравнений равновесия целесообразно использовать при определении реакций в заделке?

2. Какую форму системы уравнений равновесия целесообразно использовать при определении реакций в опорах двухопорной балки и почему?

3. Сколько уравнений равновесия необходимо составить при параллельных внешних силах?

4. Как определить равнодействующую силу равномерно распределённой нагрузки?

5. Назовите формулу для определения момента силы относительно точки.

6. Сформулируйте правила знаков для определения моментов сил.

7. Как проверить правильность определения реакций опор балочных систем?

8. В каком случае момент силы равен 0?

Курс повышения квалификации

Охрана труда

• Сейчас обучается 153 человека из 48 регионов

Курс профессиональной переподготовки

Охрана труда

• Сейчас обучается 255 человек из 57 регионов

Курс профессиональной переподготовки

Пожарная безопасность

• Сейчас обучается 136 человек из 45 регионов

«Профессиональный имидж педагога: стереотипы и методы их преодоления»

Свидетельство и скидка на обучение каждому участнику

«Мотивация здорового образа жизни. Организация секций»

Свидетельство и скидка на обучение каждому участнику

• Для всех учеников 1-11 классов
  и дошкольников
• Интересные задания
  по 16 предметам

Видео:Определение опорных реакций балки | ISopromatСкачать

Дистанционные курсы для педагогов

Самые массовые международные дистанционные

Школьные Инфоконкурсы 2022

33 конкурса для учеников 1–11 классов и дошкольников от проекта «Инфоурок»

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

5 839 774 материала в базе

Ищем педагогов в команду «Инфоурок»

Другие материалы

• 19.11.2017
• 1217
• 1

• 19.11.2017
• 644
• 8

• 19.11.2017
• 209
• 0

• 19.11.2017
• 797
• 0

• 19.11.2017
• 608
• 0

• 19.11.2017
• 497
• 2

• 19.11.2017
• 859
• 2

• 19.11.2017
• 775
• 1

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Добавить в избранное

• 19.11.2017 16286
• DOCX 1.3 мбайт
• 75 скачиваний
• Оцените материал:

Настоящий материал опубликован пользователем Свиридова Надежда Владимировна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Автор материала

• На сайте: 6 лет
• Подписчики: 0
• Всего просмотров: 37628
• Всего материалов: 7

Московский институт профессиональной
переподготовки и повышения
квалификации педагогов

Видео:БАЛКА С СИЛОЙ ПОД УГЛОМ. Реакции опор. Техническая механикаСкачать

Дистанционные курсы
для педагогов

663 курса от 690 рублей

Выбрать курс со скидкой

Выдаём документы
установленного образца!

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

Около 20% детей до 15 лет не воспринимают прочитанную информацию

Время чтения: 1 минута

Минпросвещения рекомендует школьникам сдавать телефоны перед входом в школу

Время чтения: 1 минута

С 1 сентября в российских школах будут исполнять гимн России

Время чтения: 1 минута

Российские школьники начнут изучать историю с первого класса

Время чтения: 1 минута

Опубликовано расписание ОГЭ 2022

Время чтения: 1 минута

Госдума рассматривает проект о регулировании «продленок» в школах

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Видео:Определение опорных реакций в заделке ( балка ). СопроматСкачать

Как определить реакции в опорах?

Привет! В этой статье, предлагаю поговорить о реакциях опор, еще известных как опорные реакции. Для успешного освоения курса – «сопротивление материалов», каждый студент должен уметь определять реакции в опорах, и этому уделяют особое внимание на термехе. А курс термеха, по традиции, читают до сопромата. Для тех, кто проспал механику на первом курсе, я подготовил данную статью, чтобы каждый желающий мог приобрести навыки по расчету опорных реакций.

Видео:Определение реакций опор простой рамыСкачать

Что такое реакция опоры?

Реакция опоры – это та сила, которая возникает в опоре от действия внешней нагрузки. В зависимости от конструкции опоры и ее назначения, в ней может появляться разное количество реакций, это может быть как сила, так и момент.

В начале этой статьи, расскажу о том, что должен уже уметь читатель, для успешного освоения данного урока. Если у Вас есть проблемы по поднятым вопросам на старте статьи, переходите по ссылкам на другие материалы на нашем сайте, после чего возвращайтесь к нам на чай реакции. Во второй части статьи, посмотрим, как вычисляются реакции на простейшем примере – балки, загруженной по центру сосредоточенной силой. Тут я покажу, как пользоваться уравнениями равновесия статики, как их правильно составлять. Дальше по плану, научу учитывать распределенную нагрузку, на примере той же балки. И завершать данный урок, будет пример определения реакций для плоской рамы, загруженной всевозможными типами нагрузок. Где применим уже все фишки, о которых я буду рассказывать по ходу урока. Что же, давайте начнем разбираться с реакциями!

Что вы должны уже уметь?

В этом блоке статье, я расскажу, как и обещал, что Вы должны УЖЕ уметь, чтобы понять то, что я буду докладывать дальше, про реакции опор.

Должны уметь находить сумму проекций сил

Да, это то, что Вам когда-то рассказывали на термехе, как собственно, и опорные реакции. Если Вы шарите немного в этих проекциях, то можете смело переходить к следующему пункту. Если же нет, то специально на этот случай, у меня есть другая статья, про проекции сил. Переходите, просвещайтесь, после чего, обязательно, возвращайтесь сюда!

Должны уметь составлять сумму моментов относительно точки

Немного теории! Познакомимся для начала с самим понятием момент силы. Момент силы — это произведение силы на плечо. Где плечо — это кратчайшее расстояние от точки до силы, то есть перпендикуляр. Проиллюстрирую написанное:

На изображении показано, как определить момент силы F, относительно точки O.

Так же, для моментов, нужно задаться каким-то правилом знаков. Сила относительно точки может поворачивать как по часовой стрелке, так и против нее. Я в своих уроках буду придерживаться такого правила:

• Если сила относительно точки крутит ПРОТИВ часовой стрелке, то момент положительный.
• Если она крутит ПО часовой стрелки, то соответственно момент отрицательный.

Причем, это правило условно! Какое правило Вы будете использовать совсем не важно, результат получите тот же самый. В теоретической механике, к примеру, делают также как я рассказываю.

Должны разбираться в основных видах опор

Теперь поговорим о самих опорах. В этой статье, будем работать с двумя типами опор: шарнирно-подвижной и шарнирно-неподвижной.

Шарнирно-подвижная опора препятствует вертикальному перемещению элементу конструкции, в связи с чем, в ней, под действием внешней нагрузки возникает вертикальная реакция. Обозначают ее обычно как R_i, где i — точка крепления опоры.

Шарнирно-неподвижная опора имеет две реакции: вертикальную и горизонтальную. Так как препятствует перемещению в этих двух направлениях.

Вообще-то способов закрепления элементов конструкций и их условных обозначений достаточно много, но в рамках этой статьи их рассматривать не будем.

Видео:РГЗ 2 Статика Балочные системы Определение реакций в опорахСкачать

Примеры определения сил реакций опор

Вроде, всю подготовительную информацию дал, теперь будем рассматривать конкретные примеры. И начнем с простейшей расчетной схемы балки.

Определение реакций опор для балки

Возьмем балку на двух опорах, длиной 2 метра. Загрузим ее, посередине пролета, сосредоточенной силой:

Для этой расчетной схемы, выгодно записать такое условие равновесия:
То есть, будем составлять две суммы моментов относительно опорных точек, из которых можно сразу выразить реакции в опорах. В шарнирно-неподвижной опоре горизонтальная реакция будет равна нулю, ввиду того, что горизонтальные силы отсутствуют. Последним уравнением, взяв сумму проекций на вертикальную ось, сможем проверить правильность нахождения опорных реакций, это сумма должна быть равна нулю.

Введем систему координат, пустим ось х вдоль балки, а ось y вертикально. Обозначим реакции в опорах как R_A и R_B:

Запишем уравнение моментов, относительно точки А. Сила F поворачивает ПО часовой стрелки, записываем ее со знаком МИНУС и умножаем на плечо. Сила R_B поворачивает ПРОТИВ часовой стрелки, пишем ее со знаком ПЛЮС и умножаем на плечо. Все это приравниваем к нулю:

Из полученного уравнения выражаем реакцию R_B.

Первая реакция найдена! Вторая реакция находится аналогично, только теперь уравнение моментов записываем относительно другой точки:

После нахождения реакций, делаем проверку:

Определение реакций опор для балки с распределенной нагрузкой

Теперь рассмотрим балку, загруженную распределенной нагрузкой:

Перед тем как посчитать реакции опор, распределенную нагрузку нужно свернуть до сосредоточенной силы. Если умножить интенсивность q на длину участка, на которой действует нагрузка, получим силу Q. Сила Q будет находиться ровно посередине балки, как и сила F в нашем первом примере:

Подробно комментировать нахождение реакций в опорах здесь, не буду. Просто приведу решение:

Определение опорных реакций для плоской рамы

Теперь, после освоения азов по расчету реакций, предлагаю выполнить расчет плоской рамы. Для примера, возьмем раму, загруженную всевозможными видами нагрузок:

Проводим ряд действий с расчетной схемой рамы:

• заменяем опоры на реакции;
• сворачиваем распределенную нагрузку до сосредоточенной силы;
• вводим глобальную систему координат x и y.

Для такой расчетной схемы, лучше использовать следующую форму условий равновесия:

Составив первое уравнение, относительно точки A, сразу найдем реакцию в опоре B:

Записав второе уравнение, сумму проекций на ось х, найдем горизонтальную реакцию H_A:

И, наконец, третье уравнение, позволит найти реакцию R_A:

Не пугайтесь отрицательного значения реакции! Это значит, что при отбрасывании опоры, мы не угадали с направлением этой силы.

Расчет же показал, что R_A, направленна в другую сторону:

В итоге, получили следующие реакции в опорах рамы:

Осталось проверить наши расчеты! Для этого предлагаю записать уравнение моментов, относительно точки B. И если, эта сумму будет равна нулю, то расчет выполнен верно:

Как видим, расчет реакций выполнен правильно!

На этом заканчиваю данный урок. Если у Вас остались какие-то вопросы по нахождению опорных реакций, смело задавайте их в комментариях к этой статье. Обязательно на все отвечу!

Спасибо за внимание! Если понравилась данная статья, расскажите о ней своим одногруппникам, не жадничайте 🙂

Также рекомендую подписаться на наши соц. сети, чтобы быть в курсе обновлений материалов проекта.

💡 Видео

Определение опорных реакций в простой балке. Урок №1Скачать

Определение опорных реакций в балкеСкачать

Техническая механика/Определение опорных реакций в балке на двух опорах.Скачать

Основы Сопромата. Виды опор. Определение реакций опорСкачать

Определение опорных реакцийСкачать

Определение опорных реакций балки на двух опорахСкачать

Определение реакций двухопорной балкиСкачать

Техническая механика/Определение реакций в жесткой заделке.Скачать

Видеоурок 2. Определение реакций двухопорных балок.Скачать

Определение опорных реакций в балке (балка с жесткой заделкой)Скачать

Балка. Реакции в заделке. Реакции опор. Сопромат.Скачать