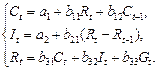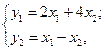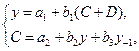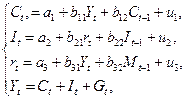Сложные экономические процессы и явления описываются с помощью системы взаимосвязанных уравнений (СОУ), в которых одни и те же переменные в различных уравнениях регресии могут одновременно выступать как в роли результирующих показателей, так и в роли объясняющих переменных.
Различают несколько видов систем уравнений:
— системы независимых уравнений – в которых каждая зависимая переменная рассматривается как функция одного и того же набора факторов :
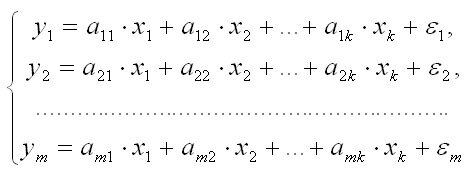
— системы рекурсивных уравнений – в которых зависимая переменная одного уравнения выступает в виде фактора в другом:
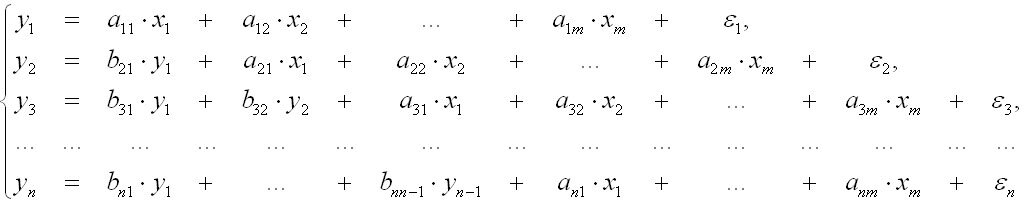
— системы совместных уравнений – в которых одни и те же зависимые переменные в одних уравнениях входят в левую часть, а в других уравнениях – в правую часть:
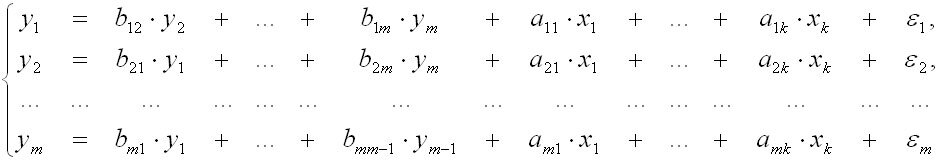
Видео:Решение систем уравнений второго порядка. 8 класс.Скачать

Эндогенные, экзогенные и предопределенные переменные
Эндогенные переменные – взаимозависимые переменные, определяемые внутри системы
Экзогенные переменные – независимые переменные, определяемые вне системы.
Предопределенные переменные – лаговые и экзогенные (за предыдущие моменты времени) эндогенные переменные системы.
Коэффициенты a и b при переменных – структурные коэффициенты модели.
Источник: Эконометрика: Учебник / Под ред. И.И. Елисеевой. – М: Финансы и статистика, 2002. – 344 с.
Для получения дополнительной информации по эконометрике жмите сюда.
Видео:Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

Виды систем эконометрических уравнений (СЭУ)
Объектом статистического изучения в социальных науках являются сложные системы. Система эконометрических уравнений включает в себя 1 или несколько уравнений регрессии и может включать в себя также выражения, называемые тождествами. Обычно в систему включаются уравнения линейной регрессии и тождества (- это функция, отражающая функцион.связь показателей, не содержащая независ.параметров) в линейной форме.
Если в систему входит 1 уравнение регрессии, то оно всегда доп-но тождествами, а если неск-ко, то тождество необязательно.
Совокупность выражений, входящих в СЭУ отражает комплекс взаимосвязей к-го-то эконом. Явления. Поэтому систему называют структурной формой модели.
В рамках СЭУ вводится новая классификация переменных (экзогенные, эндогенные и лаговые переменные)
Система уравнений в эконометрических исследованиях может быть построена по-разному.
1. Самая простая – система независимых уравнений, когда каждая зависимая переменная у рассматривается как функция одного и того же набора факторов х:
Набор факторов xi в каждом уравнении может варьироваться. Например, модель вида
Также является системой независимых уравнений с отличием в том, что в ней набор факторов видоизменяется в уравнениях, входящих в систему. Отсутствие одного их факторов может объясняться нецелесообразностью включения его в модель, несущественностью его воздействия на результативный признак и др. Каждое уравнение такой системы может рассматриваться самостоятельно. Для нахождения его параметров используется метод наименьших квадратов.
2. Система рекурсивных уравнений –система, когда зависимая переменная у одного уравнения выступает в качестве фактора х в другом уравнении. В этом случае последующий результат зависит от всех факторов и предыдущих результатов:
В данной системе зависимая переменная у включает в каждое последующее уравнение в качестве факторов все зависимые переменные предшествующих уравнений наряду с набором собственно факторов х. Как и в предшествующей модели уравнение может рассматриваться самостоятельно, и его параметры определяются методом наименьших квадратов. В этой сис-ме уравнение можно упорядочить, т.о, чтобы рез-т текущего уравнения входил в качестве факторов во все последующие уравнения.
- Система совместных или одновременных уравнений (система взаимозависимых переменных) – наибольшее распространение в эконометрических исследованиях. В ней одни и те же зависимые переменные в одних уравнениях входят в левую часть, а в других – в правую часть системы:
В системе одни и те же переменные у рассматриваются как зависимые в одних уравнениях и как независимые в других. В эконометрике эта модель также называется структурной формой модели. В отличие от предыдущих систем каждое уравнение данной модели не может рассматриваться самостоятельно, и для нахождения его параметров МНК неприменим. Используются специальные приемы оценивания (например, с помощью матрицы параметров).
В системе одноврем.уравнений каждый рез-т (эндогенная переменная) зависит от рез-в др.уравнений.различают СОУ в полной и неполной форме
53. Структурная форма модели: состав, виды переменных.
Исходная система (модель), которая отражает реальные связи между показателями, называется структурной формой модели (СФМ).
СФМ содержит эндогенные и экзогенные переменные.
Переменные, которые являются только факторами во всех уравнениях модели, называются экзогенными (х1,х2).
Переменные, кот1орые хотя бы в одном из уравнений системы являются результатом, называются эндогенными (у1,у2).
Простейшая структурная форма модели имеет вид:
Классификация переменных на эндогенные и экзогенные зависит от теоретической концепции принятой модели. Экономические переменные могут выступать в одних моделях как эндогенные, а в других – как экзогенные. Внеэкономические переменные (например, климатические условия) входят в систему как экзогенные переменные.
В качестве экзогенных переменных могут рассматриваться значения эндогенных переменных за предшествующий период времени – это лаговые переменные. Так, например, потребление текущего года (уt) может зависеть не только от ряда экономических факторов, но и от уровня потребления в предыдущем году (уt-1).
Структурная форма модели позволяет увидеть влияние изменений любой экзогенной переменной на значения эндогенной переменной. Структурная форма модели содержит в правой части при эндогенных и экзогенных переменных коэффициенты bi (коэффициент при эндогенной) и aj (при экзогенной), которые называются структурные коэффициенты модели. Все переменные в модели выражены в отклонениях от среднего уровня, т.е. под x подразумевается 
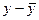
54. Приведенная форма модели: структура, предназначение, связь с приведенной формой.
Так как использоьвание МНК для оценивания структурных коэффициентов модели дает, как принято считать в теории, смещенные и несостоятельные оценки. Поэтому обычно для определения структурных коэффициентов модели структурная форма модели преобразуется в приведенную форму модели.
Приведенная форма модели представляет собой систему линейных функций эндогенных переменных от экзогенных:
Где 
По виду приведенная форма ничем не отличается от системы независимых уравнений, параметры которой оцениваются традиционным способом МНК. Применяя МНК, можно оценить 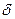
Коэффициенты приведенной формы модели представляют собой нелинейные функции коэффициентов структурной формы модели. Коэффициенты приведенной функции выражаются из модели структурной.
Так, например, структурная модель имеет вид:
Приведенная форма модели имеет вид:
У2 из первого уравнения структурной формы можно выразить как:
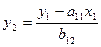
Отсюда имеем равенство:

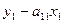


Таким образом, мы представили первое уравнение структурной формы модели в виде уравнения формы модели:
Т.е. мы выразили коэффициенты приведенной формы уравнения через соотношения коэффициентов структурной формы:

Аналогично доказываем связь коэффициентов приведенной формы модели второго уравнения с коэффициентами структурной модели:

Приведенная форма модели хотя и позволяет получить значения эндогенной переменной через значения экзогенных переменных, аналитически уступает структурной форме модели, так как в ней нет оценки взаимосвязи между эндогенными переменными.
Видео:Симметричные системы #1Скачать

СИСТЕМЫ ЭКОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ
Практическое занятие 1
Сложные экономические процессы описывают с помощью системы взаимосвязанных (одновременных) уравнений.
Различают несколько видов систем уравнений:
— система независимых уравнений – когда каждая зависимая переменная y рассматривается как фунуция одного и того же набора факторов х:
Для решения этой системы и нахождения ее параметров используется метод наименьших квадратов;
— система рекурсивных уравнений – когда зависимая переменная у одного уравнения выступает в виде факторах в другом уравнении:
Для решения этой системы и нахождения ее параметров используется метод наименьших квадратов;
— система взаимосвязанных (совместных) уравнений – когда одни и те же зависимые переменные в одних уравнениях входят в левую часть, а в других – в правую:
Такая система уравнений называется структурной формой модели.
Эндогенные переменные – взаимозависимые переменные, которые определяются внутри модели (системы) у.
Экзогенные переменные – независимые переменные, которые определяются вне системы х.
Предопределенные переменные – экзогенные и лаговые (за предыдущие моменты времени) эндогенные переменные системы.
Коэффициенты а и b при переменных – структурные коэффициенты модели.
Система линейных функций эндогенных переменных от всех
предопределенных переменных системы – приведенная форма модели:
где δ – коэффициенты приведенной формы модели.
Необходимое условие идентификации – выполнение счетного правила:
D + 1 = Н – уравнение идентифицируемо;
D + 1 И – уравнение сверхидентифицируемо,
где Н – число эндогенных переменных в уравнении,
D – число предопределенных переменных, отсутствующих в уравнении, но присутствующих в системе.
Достаточное условие идентификации – определитель матрицы, составленной из коэффициентов при переменных, отсутствующих в исследуемом уравнении, не равен нулю, и ранг этой матрицы не менее числа эндогенных переменных системы без единицы.
Задачи для самоконтроля
Определить вид системы уравнений. Оценить следующую структурную модель на идентификацию:
Определить вид системы уравнений. Проверить идентификацию системы эконометрических уравнений.
Если: а) все параметры системы отличны от нуля;
Определить вид системы уравнений. Проверить идентификацию системы эконометрических уравнений.
Если: а) все параметры системы отличны от нуля;
Практическое занятие 2
Коэффициенты структурной модели могут быть оценены различными способами в зависимости от вида системы одновременных уравнений. Наибольшее распространение получили следующие методы:
— косвенный метод наименьших квадратов (КМНК);
— двухшаговый метод наименьших квадратов (ДМНК);
— трехшаговый метод наименьших квадратов (ТМНК).
Для решения идентифицируемого уравнения применяется косвенный метод наименьших квадратов. Он заключается в следующем:
— составляют приведенную форму модели и определяют численные значения параметров каждого ее уравнения обычным МНК;
— путем алгебраических преобразований переходят от приведенной формы к уравнениям структурной формы модели, получая тем самым численные оценки структурных параметров.
Например, требуется найти структурные параметры модели
при условии, что полученная приведенная форма модели описывается уравнениями
Проверим идентифицируемость уравнений. В модели имеется две эндогенные переменные y1, y2 и две экзогенные переменные x1, x2. В первое уравнение входят две эндогенные переменные у1, у2 и одна экзогенная переменная x2. Следовательно, H = 2, D = 1 и H = D + 1, и первое уравнение – идентифицируемо. Идентифицируемость второго уравнения доказывается аналогично. Для нахождения структурных коэффициентов можно применить косвенный МНК, т. е. получить их с помощью преобразования приведенных уравнений.
Для этого из 2-го уравнения приведенной формы выразим переменную x2 = x1 – y2 и подставим в 1-е уравнение приведенной формы модели
Сравнивая это уравнение с 1-м уравнением структурной формы
y1 = b12y2 + a11x1, определим значения структурных параметров
Далее из первого уравнения приведенной формы выразим переменную x1 = 0,5y1 – 2x2 и подставим во 2-е уравнение приведенной формы модели
Сравнивая последнее уравнение с 2-м структурной формы
y2 = b21y1 + a22x2, получим
Таким образом, структурная форма модели определяется уравнениями:
Задачи для самоконтроля
Рассматривается макроэкономическая модель:
где y1 – валовой региональный продукт (млрд. руб.);
y2 – инвестиции в основной капитал (млрд. руб.);
y3 – валовая прибыль экономики (млрд. руб.);
x1 – численность занятых в экономике (млн. чел.);
x2 – темп роста объема промышленной продукции (%);
x3 – инвестиции в основной капитал предыдущего года (млрд. руб.).
1. Проведите идентификацию модели (двумя способами).
2. Укажите способ оценки параметров каждого уравнения системы.
3. Найдите структурные коэффициенты первого уравнений системы, если известна система приведенных уравнения:
4. Опишите методику оценки параметров третьего уравнения системы.
Рассматривается следующая модель:
где C – объем потребления;
I – объем инвестиций;
G − объем государственных расходов.
1. Представьте данную систему в приведенной форме.
2. Определите, какие из структурных уравнений идентифицируемы?
3. Какой метод можно использовать для оценки параметров рассматриваемой модели?
Рассматривается следующая модель «спрос – предложение»:
где qt, pt – эндогенные переменные – количество товара и цена в году t;
yt – экзогенная переменная – доход потребителей;
На основании следующих статистических данных необходимо оценить коэффициенты функции предложения, используя для этого МНК и КМНК. Сравнить результаты.
| pt | qt | yt |
| сумма | ||
| 6,2 | 3,2 | среднее |
Имеются данные, характеризующие некоторое государство за семь последовательных лет:
| № | Темп прироста | % безработных, x1 | ||
| Заработной платы, у1 | цен, у2 | дохода, у3 | цен на импорт, x2 | Экономически активного населения, x3 |
Определите параметры структурной модели вида:
Имеются данные, характеризующие годовое потребление мяса на душу населения, средние потребительские цены, среднедушевые денежные доходы, индекс цен производителей:
| Год | Годовое потребление мяса на душу населения, кг, y1 | Средние потребительские цены на мясо, руб. за кг., у2 | Среднедушевые денежные доходы населения в месяц, руб., x1 | Индекс цен производителей на мясо, %, x2 |
| 246,05 | 196,7 | |||
| 255,7 | ||||
| 256,25 | 137,6 | |||
| 282,55 | 105,2 | |||
| 293,55 | 102,6 |
Необходимо построить модель вида:
рассчитав соответствующие структурные коэффициенты модели.
Практическое занятие 3
Для решения сверхидентифицированных уравнений применяется двухшаговый МНК (ДМНК), который заключается в следующем:
— составляют приведенную форму модели и определяют численные значения параметров каждого ее уравнения обычным МНК;
— выявляют эндогенные переменные, находящиеся в правой части структурного уравнения, параметры которого определяют двухшаговым МНК, и находят расчетные значения по соответствующим уравнениям приведенной формы модели;
— обычным МНК определяют параметры структурного уравнения, используя в качестве исходных данных фактические значения предопределенных переменных и расчетные значения эндогенных переменных, стоящих в правой части данного структурного уравнения.
Рассмотрим в качестве примера модифицированную модель Кейнса:
где Ct, Yt, It и Gt – объем потребления, совокупный доход, инвестиции и государственные расходы соответственно;
α и β – структурные коэффициенты;
Разрешая структурную систему относительно эндогенных переменных, получим приведенную систему уравнений вида:


Двухшаговый МНК можно рассматривать как частный случай метода инструментальных переменных. При описании применения метода инструментальных переменных было указано, что структурное уравнение функции потребления оказалось переопределенным, и сразу две переменные It и Gt могли быть использованы для определения функции Yt.
Однако вместо их раздельного применения можно предложить их комбинацию:
Вместо zt может быть выбрана регрессионная оценка Ŷt, приведенного уравнения для Yt, которую получают с помощью обычного МНК:
Так осуществляется первый шаг двухшагового метода наименьших квадратов. Подставляя теоретические значения Ŷt вместо фактических значений в структурное уравнение функции потребления, получим уравнение:
Оценки параметров аир этого уравнения получают с помощью обычного МНК. Так осуществляется второй шаг двухшагового метода наименьших квадратов. При этом оценки структурных коэффициентов будут состоятельными.
Двухшаговый МНК можно рассматривать как способ конструирования наилучшей из возможных комбинаций инструментальных переменных, если в уравнении имеется избыток экзогенных переменных, которые можно использовать как инструментальные.
Более эффективным, но требующим существенно больших вычислительных затрат, является трехшаговый метод наименьших квадратов (ТМНК). Он заключается в том, что двухшаговый метод наименьших квадратов применяется не к исходным уравнениям модели, а к уравнениям, преобразованным согласно обобщенному методу наименьших квадратов. Трехшаговый МНК является итерационной процедурой:
1) Параметры модели определяются обычным или двухшаговым МНК.
2) Вычисляются ошибки модели и определяется оценка корреляционной матрицы ошибок.
3) Уравнения преобразуются согласно обобщенному МНК.
4) Применяется двухшаговый МНК к преобразованным уравнениям и получается улучшенная модель (с улучшенными параметрами).
5) Процесс повторяется, начиная со второго шага, пока не будет достигнута заданная точность (либо превышено заданное количество итераций).
Если случайные члены структурной модели не коррелируют, то трехшаговый метод сводится к двухшаговому.
Задачи для самоконтроля
Имеются данные, характеризующие некоторое государство за семь последовательных лет:
| № | Темп прироста | % безработных, x1 | ||
| Заработной платы, у1 | цен, у2 | дохода, у3 | цен на импорт, x2 | Экономически активного населения, x3 |
Определите параметры структурной модели вида:
Изучается модель вида:
где y – валовой национальный доход;
y-1 – валовой национальный доход предшествующего года;
C – личное потребление;
D – конечный спрос (помимо личного потребления).
Дана следующая информация за девять лет о приростах всех показателей:
| Год | D | y-1 | y | С |
| -0,8 | 40,7 | 3,1 | 7,4 | |
| 22,4 | 3,1 | 22,8 | 30,4 | |
| -17,3 | 22,8 | 7,8 | 1,3 | |
| 12,0 | 7,8 | 21,4 | 8,7 | |
| 5,0 | 21,4 | 17,8 | 25,8 | |
| 44,7 | 17,8 | 37,2 | 8,0 | |
| 23,1 | 37,2 | 35,7 | 30,0 | |
| 51,2 | 35,7 | 40,0 | 31,4 | |
| 32,3 | 40,0 | 50,0 | 30,1 | |
| I | 107,5 | 230,1 | 248,4 | 182,7 |
Для данной модели была получена система приведенных уравнений:
– провести идентификацию модели;
– рассчитать параметры первого уравнения структурной модели.
Построена следующая модель:
где Kt – стоимость основных фондов (эндогенная переменная);
Yt – количество работающих (эндогенная переменная);
It – объем инвестиций (экзогенная переменная);
Pt – объем продукции (эндогенная переменная);
Xt – использование сырья (экзогенная переменная).
Имеются наблюдения за 11 лет:
| t | Pt | Yt | Kt | Xt | It |
| 4Д | 2,8 | 1,2 | |||
| 4Д | 2,9 | 1,3 | |||
| 4,2 | 3,8 | 1,3 | |||
| 4,4 | 4,1 | 1Д | |||
| 4,6 | 4,1 | 1,3 | |||
| 4,6 | 4,1 | 1,4 | |||
| 4,7 | 4,0 | 1,3 | |||
| 4,8 | 4,1 | 1,6 | |||
| 5,2 | 4,2 | 1,8 | |||
| 5,4 | 4,2 | 1,9 | |||
| 5,8 | 4,3 | 2,0 |
– провести идентификацию модели;
– рассчитать параметры уравнений структурной модели;
– рассчитать стандартные ошибки полученных параметров.
Дана модифицированная модель Кейнса:
где C – потребление; Y – доход; I – инвестиции; G – государственные расходы; t – текущий период; t-1 – предыдущий период.
| Годы | Y | C | I |
| 95,75 | 60,45 | 14,3 | |
| 92,55 | 62,45 | 15,25 | |
| 103,55 | 65,9 | 17,75 | |
| 62,9 | 19,7 | ||
| 108,25 | 62,45 | 12,1 | |
| 107,4 | 14,6 | ||
| 112,7 | 73,55 | 17,35 | |
| 117,75 | 76,55 | ||
| 123,45 | 79,7 | 22,15 | |
| 126,55 | 21,6 | 22,3 | |
| 125,25 | 21,55 | 19,2 | |
| 122,1 | 22,55 | ||
| 125,35 | 23,45 | ||
| 130,25 | 27,35 | 2D | |
| 132,3 | 91,55 | 25,25 | |
| 142,65 | 95,5 | ||
| 145,2 | |||
| 151,3 | 101,75 | ||
| 157,4 | 105,4 | 25,2 | |
| 161,25 | 107,45 | 26,15 |
1. В предположении, что потребление зависит линейно от дохода (первое уравнение модели), оцените по МНК параметры a1 и b11 функции потребления;
2. Оцените те же параметры по ДМНК и по ТМНК;
3. Сравните полученные результаты. Сделайте выводы по качеству оценок.
Рассматривается следующая модель:
где Сt – расходы на потребление в период t;
Yt – совокупный доход в период t;
rt – процентная ставка в период t;
Мt – денежная масса в период t;
Gt – государственные расходы в период t;
1. В предположении, что имеются временные ряды данных по всем переменным модели, предложите способ оценки ее параметров.
2. Как изменится ваш ответ на вопрос п. 1, если из модели исключить тождество дохода?
АНАЛИЗ ВРЕМЕННЫХ РЯДОВ
Практическое занятие 1
Модели, построенные по данным, характеризующим один объект за ряд последовательных моментов (периодов), называются моделями временных рядов.
Временной ряд – это совокупность значений какого-либо показателя за несколько последовательных моментов или периодов.
Каждый уровень временного ряда формируется из трендовой (T), циклической (S) и случайной (Е) компонент.
Модели, в которых временной ряд представлен как сумма перечисленных компонент, – аддитивные модели, как произведение – мультипликативные модели временного ряда.
Аддитивная модель имеет вид: Y = Т + S + Е;
Мультипликативная модель: Y = T • S • E.
Автокорреляция уровней ряда – это корреляционная зависимость между последовательными уровнями временного ряда:

где 


где 

Формулы для расчета коэффициентов автокорреляции старших порядков легко получить из формулы линейного коэффициента корреляции.
Последовательность коэффициентов автокорреляции уровней первого, второго и т.д. порядков называют автокорреляционной функцией временного ряда, а график зависимости ее значений от величины лага (порядка коэффициента автокорреляции) – коррелограммой.
Построение аналитической функции для моделирования тенденции (тренда) временного ряда называют аналитическим выравниванием временного ряда. Для этого чаще всего применяются следующие функции:
• экспонента ŷt =e a + b • t ;
• степенная функция ŷt =a • t b ;
• парабола второго и более высоких порядков ŷt =a + b1 • t + b2 • t 2 +. + bk • t k .
Параметры трендов определяются обычным МНК, в качестве независимой переменной выступает время t = 1,2, . n, а в качестве зависимой переменной – фактические уровни временного ряда уt. Критерием отбора наилучшей формы тренда является наибольшее значение скорректированного коэффициента детерминации 
Задачи для самоконтроля
Приведены данные, отражающие спрос (штук) на некоторый товар за двенадцатилетний период, т.е. временной ряд спроса.
| Год, t |
| Спрос, yt |
Найти коэффициенты автокорреляции первого, второго и третьего порядков.
По данным задачи 1 выявить с помощью МНК линейную тенденцию.
Имеются следующие данные об уровне безработицы уt (%) за 8 месяцев:
| Месяц | ||||||||
| yt | 8,8 | 8,6 | 8,4 | 8,1 | 7,9 | 7,6 | 7,4 | 7,0 |
Определите коэффициенты автокорреляции уровней этого ряда первого и второго порядка.
Имеется следующий временной ряд:
| t | ||||||
| xt | … | … | … | … | … | … |
Известно, что 


1. Определите коэффициент автокорреляции уровней этого ряда первого порядка.
2. Установите, включает ли исследуемый временной ряд тенденцию.
Дана выборка курса биржевой стоимости акции некоторого предприятия за 12 месяцев:
| Стоимость акции по месяцам (руб.) | ||||||||||||
| Месяц, t | ||||||||||||
| Стоимость, yt | 13,1 | 11,9 | 11,8 | 17,3 | 15,9 | 16,1 | 20,5 | 19,2 | 19,9 | 23,9 | 22,8 | 23,8 |
1. Найти коэффициенты автокорреляции со смещением на 1,2,3 и 4 месяца.
2. Проверить найденные коэффициенты автокорреляции на значимость с доверительной вероятностью p = 0,95.
3. Построить коррелограмму.
4. Построить модель тенденции временного ряда.
Практическое занятие 2
При построении моделей регрессии по временным рядам для устранения тенденции используются следующие методы.
Метод отклонений от тренда предполагает вычисление трендовых значений для каждого временного ряда модели, например ŷt и 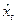
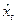
Метод последовательных разностей заключается в следующем: если ряд содержит линейный тренд, тогда исходные данные заменяются первыми разностями:
Если параболический тренд – вторыми разностями:
В случае экспоненциального и степенного тренда метод последовательных разностей применяется к логарифмам исходных данных.
Модель, включающая фактор времени, имеет вид:
Автокорреляция в остатках – корреляционная зависимость между значениями остатков ε, за текущий и предыдущие моменты времени.
Для определения автокорреляции остатков используют критерий Дарвина — Уотсона и расчет величины:

Коэффициент автокорреляции остатков первого порядка определяется по формуле:


Критерий Дарбина — Уотсона и коэффициент автокорреляции остатков первого порядка связаны соотношением
d = 2(1 – 
Если автокорреляция остатков отсутствует (r = 0) – d
2. При положительной автокорреляции (r > 0) имеем 0 .
📽️ Видео
симметрические системы уравненийСкачать

Решение систем уравнений второй степени. Алгебра, 9 классСкачать

Система с тремя переменнымиСкачать

После этого видео, ТЫ РЕШИШЬ ЛЮБУЮ Систему Нелинейных УравненийСкачать

Решение биквадратных уравнений. 8 класс.Скачать

Решение систем уравнений методом подстановкиСкачать

Решение системы линейных уравнений с двумя переменными способом подстановки. 6 класс.Скачать

9 класс, 11 урок, Методы решения систем уравненийСкачать

Алгебра 7 класс (Урок№45 - Уравнения первой степени с двумя неизвестными.)Скачать

МЕТОД ПОДСТАНОВКИ 😉 СИСТЕМЫ УРАВНЕНИЙ ЧАСТЬ I#математика #егэ #огэ #shorts #профильныйегэСкачать

Уравнение с двумя переменными и его график. Алгебра, 9 классСкачать

Системы уравнений Тема3 С истемы ур-й в которых одно ур-е 1ой степени а другие 2ой и более высокой.Скачать

Алгебра 9 класс (Урок№25 - Решение систем уравнений второй степени.)Скачать

Алгебра 7 класс (Урок№47 - Равносильность уравнений и систем уравнений.)Скачать

Решение системы линейных уравнений графическим методом. 7 класс.Скачать

Алгебра 10 класс (Урок№14 - Алгебраические системы уравнений.)Скачать

Как решить функциональное уравнение f(x)+f(1/(1−x))=x, где f(x) определена везде, кроме точек 0 и 1?Скачать