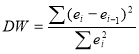ЛАБОРАТОРНАЯ РАБОТА № 2
Цель работы: построить на основе статистических данных с помощью прикладного программного пакетадляэконометрического моделирования GRETL-1.9.92 парное линейное уравнение регрессии, оценить качество модели, и, если оно будет удовлетворительным, сделать прогноз.
Доверительный интервал для неизвестного параметра линейного уравнения регрессии A:
Аналогичное определяется доверительные интервал для параметра B:
Для оценки статистической значимости коэффициента регрессии и корреляции используется 
Проверяется нулевая гипотеза 
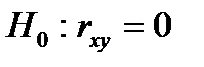




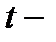


Здесь 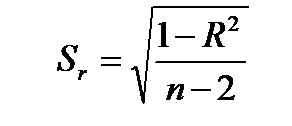





Если 



Если 
1.2. Для оценки статистической значимости найденных МНК параметров уравнения регрессии 

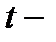
Выдвигается нулевая гипотеза 

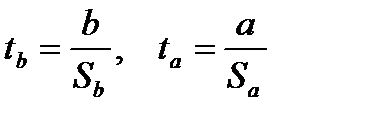
и сравнивают с критическим значением 

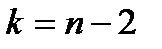
Если наблюдаемые значения 
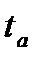



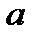
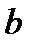
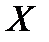

1.3. Оценка статистической значимости уравнения в целом проводится с помощью 
При проверки статистической значимости уравнения регрессии с помощью критерия Фишера проверяется нулевая гипотеза 
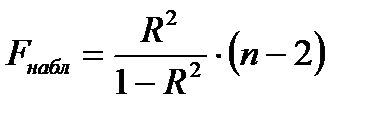


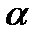


Нулевая гипотеза отклоняется, если 


Различают точечное и интервальное прогнозирование. В первом случае оценка – некоторое число, а во втором – интервал, в котором находится истинное значение зависимой переменной с заданным уровнем значимости.
Пусть 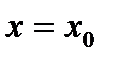


Доверительный интервал для среднего значения:
здесь 



Моделирование в данной работе будет осуществляться на основе прикладного программного пакетаGRETL-1.9.92.Пакет программ GRETL (GNU Regression Econometrics and Time Series Library) представляет собой инструментарий дляпостроения и анализа эконометрических моделей.Данный программный пакетнаходится в свободном доступе. Сайт разработчика:http://gretl.sourceforge.net.
1. Основные описательные статистики (среднее арифметическое, медиана, минимальное и максимальное значения, среднеквадратическое отклонение, коэффициент вариации, коэффициент асимметрии, коэффициент эксцесса).
2. Проверка нормальности распределения, распределение частот случайной величины, распределение плотности вероятностей, определение коэффициентов корреляции и т.д.
3. Предусматривает непосредственный доступ к статистическим таблицам. Пакет Gretl содержит встроенные статистические таблицы для следующих распределений: нормального, t-распределения Стьюдента, F-распределения Фишера, хи-квадрат, Пуассона, биномиального и распределения Дарбина-Уотсона. Существует возможность вычисления критических значений, p-value.
4. Анализ временных рядов (набор методов оценивания обобщённым МНК, модели ARMAX и GARCH , система уравнений авторегрессии (VAR), проверка коинтеграции; построение линии тренда, коррелограммы, периодограммы; проверка единичных корней, моделирование типа ARIMA, а также процедуры десезонализации X-12-ARIMA и TRAMO).
5. Регрессионный анализ (одношаговый метод наименьших квадратов (МНК), взвешенный МНК, двухшаговый МНК – оценка систем одновременных уравнений, методы оценивания логитовых, пробитовых и тобитовых моделей и нелинейных моделей, и т.д.).
6. Метод главных компонент.
7. Экспорт и импорт Gretl-Microsoft Excel и текстовые редакторы (Notepad и т.д).
8. Построение графиков.
Запуск программы осуществляется через Пуск-Программы-Gretl-Gretl или двойным щелчком мыши по иконке Gretl на рабочем столе.
Стартовый экран пакета программ GRETL (рис. 1) подразделяется на три части:
1. Меню, из которого реализуется набор функций.Меню функций состоит из следующих разделов: Файл, Инструменты, Данные, Вид, Добавить, Выборка, Переменная, Модель, Справка. Каждый раздел содержит группу программных функций.
2. Список переменных (процессов), который содержит перечень названий и описаний переменных открытого набора данных.
3. Набор иконок (расположены внизу стартовой страницы) обеспечивает быстрый доступ к выбранным программным функциям:



Рис. 1.








По территориям региона приводятся данные 199Х г.
| Номер региона |
| Среднедушевой прожиточный минимум, в день одного трудоспособного, руб., х |
| Среднедневная заработная плата, руб., у |
1.Найти параметры 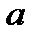
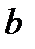
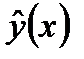
2.Найти коэффициент детерминации.
3.Рассчитать линейный коэффициент парной корреляции, оценить степень тесноты связи, используя таблицу Чеддока.
4.Оценить статистическую значимость уравнения регрессии в целом, используя F–статистику Фишера на уровне значимости 0,05.
5.Рассчитать доверительные интервалы параметров уравнения регрессии с 95% надежностью.
6.Вычислить прогнозное значение 

7.Оценить точность прогноза, рассчитав ошибку прогноза и его доверительный интервал.
8.Полученные результаты изобразить графически и привести экономическое обоснование.
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
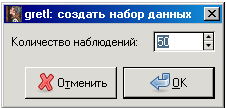
1. Сначала необходимо ввести статистические данные. Для это перейдите в раздел Файл, затем Создать. Появится диалоговое окно:
В поле Количество наблюдений введите число пар значений статистических данных, которые анализируются в данной работе.
В новом окне выберите Перекрестные данные. Затем нажмите кнопку 
Поставьте флажок в поле Начать ввод данных, затем нажмите 
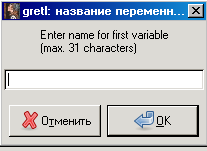
В свободном поле необходимо ввести наименование первой переменной латинскими буквами, например X. Нажмите OK.
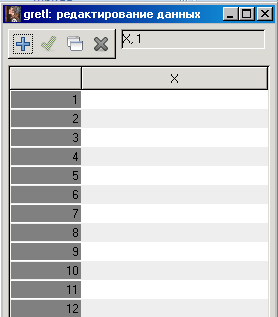
Введите данные, соответствующие переменной X во второй столбец. Затем нажмите на кнопку Добавить, перейдете на вкладку Добавить переменную. Введите название второй переменной и введите ее значения. Нажмите кнопку Применить 
2. Найдите параметры парного линейного уравнения регрессии методом наименьших квадратов.
В Менювыберите разделМодель,затем перейдите на вкладкуМетод наименьших квадратов:
В новом диалоговом окне задайте зависимые переменные и регрессоры с помощью стрелок 

Затем нажмите кнопку 
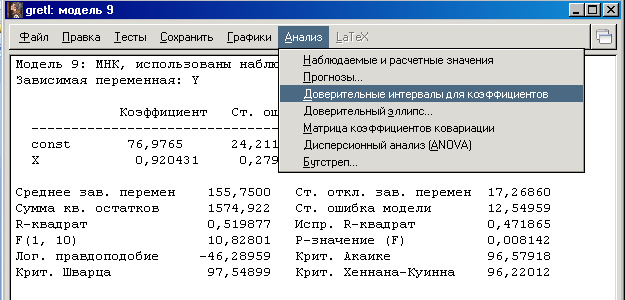
Появится окно с результатами расчета основных показателей парного линейного уравнения регрессии методом наименьших квадратов (МНК).
Запишите уравнение регрессии в бланк отчета. Параметры уравнения регрессии a и b находятся в столбце с названием «Коэффициент». Сделайте вывод, используя экономический смысл выборочного коэффициента регрессии
3. Запишите в бланк отчета значение коэффициента детерминации 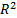
4. Рассчитаете выборочный коэффициент парной корреляции, оцените степень тесноты и направление линейной связи, используя таблицу Чеддока.
Для этого щелкните мышкой по иконке 

5. Оцените статистическую значимость уравнения регрессии в целом, используя F–статистику Фишера на уровне значимости 0,05. Наблюдаемое значение F-критерия находится в таблице с результатами расчета МНК (F(1, 10)).
Для нахождения табличного (критического) значения критерия Фишера перейдите в раздел Инструменты главного меню, затем на вкладку Критические значения. Затем выберите вкладку Фишера. Заполните следующим образом диалоговое окно:
Нажмите 
6. Рассчитайте доверительные интервалы параметров уравнения регрессии с 95% надежностью.
В окне с результатами МНК перейдите в раздел Анализ, а затем на вкладку Доверительные интервалы для коэффициентов:
Появится таблица с результатами интервальной оценки. Запишите результаты в бланк отчета.
По умолчанию расчет ведется с необходимой 95%-й надежностью. Если необходимо изменить уровень надежности, то в меню окна Доверительные интервалы для коэффициентов необходимо щелкнуть левой кнопкой мышки по иконке 
7. Вычислить прогнозное значение 

Необходимо в окне с результатами МНК перейдите в раздел Анализ, а затем на вкладку Прогнозы:
Появится новое диалоговое окно. Заполните окно так как показано на приведенном ниже рисунке, затем нажмите 
Появятся два окна: «Прогнозы», в котором приведены результаты расчетов, и «График».
Запишите в отчет точечный прогноз для 

Запишите в бланк отчета значение предельной ошибки и интервальную оценку прогноза.
Перерисуйте график в бланк отчета с уравнением регрессии и прогнозным интервалом. График можно преобразовать. Для этого нажмите правой кнопкой мышки, появится контекстное меню, затем перейдите на вкладку Правка.
Чтобы сделать прогноз для значения x, которого нет в исходных данных необходимо добавить в выборку еще одно наблюдение: данные—добавить наблюдение—изменить значение. В появившемся окне вводим количество новых наблюдений, в данном случае одно. Вводим значение x0 = 120.
Затем необходимо повторить процедуры построения МНК-модели. Для прогнозирования переходим в раздел Анализ – Прогнозы – Ок.
Запишите в бланк отчета результаты точечного и интервального прогнозирования.
1. Интервальная оценка параметров линейного уравнения регрессии.
2. Уровень значимости, уровень надежности и их взаимосвязь.
3. Проверка на статистическую значимость параметров линейного уравнения регрессии с помощью критерия Стьюдента.
4. На какие слагаемые раскладывается общая сумма квадратов отклонений результативного признака от средних значений. Чему равно число степеней свободы остаточной, общей и факторной суммы квадратов.
5. Проверка статистической значимости уравнения регрессии в целом с помощью 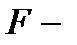
6. Прогнозирование в эконометрике. Точечное и интервальное прогнозирование. Ошибка прогноза.
Видео:Системы одновременных эконометрических уравненийСкачать

Решение задач по эконометрике в Gretl
GRETL (GNU Regression, Econometrics and Time-series Library — Библиотека для регрессий, эконометрики и временных рядов) — прикладной программный пакет (ППП) для эконометрического моделирования.
GRETL является программным обеспечением, лицензия которого разрешает легально и бесплатно копировать как исходный, так и конечный код, а также самостоятельно модифицировать исходный код.
Согласно правилам FreeSoftwareFoundation, ввиду бесплатного лицензирования пакета программ на него не распространяются гарантии действующего законодательства. Относительно качества и точности функционирования пакета программ рискует только его пользователь. Однако применение пакета программ GRETL оказывается привлекательным благодаря многочисленным положительным рецензиям, публикуемым в различных экономстрических изданиях.
Видео:Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

Начало работы в GRETL
В начале работы с пакетом программ GRETL необходимо, в первую очередь, создать или открыть набор статистических данных. Каждый набор данных должен иметь один из трех типов: срезы данных (определяемые как undated), не привязанные к моментам времени; временные ряды с фиксацией периодичности наблюдений (годовые, квартальные, ежемесячные, еженедельные, ежедневные и почасовые); панельные данные — срезово-временные.
Новый набор данных создается средствами пакета программ GRETL при помощи функции File/Createdataset, объявляющей один из представленных ниже типов данных
Построение набора данных в виде временного ряда (англ. time—series) начинается с вписывания начального (например, 1990:01) и конечного (например, 2003:12) моментов, а также выбора названия первой базовой переменной.
Ручной ввод информации с клавиатуры — достаточно трудоемкое занятие, поскольку данные в каждой ячейке должны редактироваться отдельно.
Гораздо проще создавать базу фактических (не генерируемых) данных путем, импорта из заранее подготовленной таблицы EXCEL или из текстового файла, но не путем ввода данных непосредственно с клавиатуры. Импортировать можно только данные в формате xls (Excel не выше 2003)
В расчетах были использованы данные по индексу потребительских цен в зависимости от ряда экономических данных.
Файл EXCEL должен быть подготовлен следующим образом. В первой строке должны описываться переменные процессы, а в столбцах — приводиться числовые данные. В считываемой таблице EXCEL не должно храниться никаких данных помимо поименованных столбцов, поскольку отсутствие заголовка — названия столбца — приведет к некорректному импорту данных.
Источник: Куфель Т. Эконометрика: решение задач с применением пакета программ GRETL. Монография, Варшава, 2007, 200 с.
Видео:ФСР. Система однородных уравнений. Общее решениеСкачать

Пример решения эконометрической задачи в Gretl
Ниже приведено условие задачи и текстовая часть решения. Закачка полного решения, файлы doc и gdt в архиве rar, начнется автоматически через 10 секунд. Еще примеры решения задач по эконометрике можно посмотреть здесь.
Если хотите научиться решать эту задачу в Gretl самостоятельно — вот видеоурок.
Построение эмпирического уравнения регрессии является начальным этапом эконометрического анализа. Первое же построенное по выборке уравнение регрессии очень редко является удовлетворительным по тем или иным характеристикам. Поэтому следующей задачей эконометрического анализа является проверка качества уравнения регрессии. В эконометрике принята устоявшееся схема такой проверки (по крайней мере на начальной стадии). Это нашло отражение почти во всех современных эконометрических пакетах.
Проверка статистического качества оцениваемого уравнения регрессии проводится по следующим направлениям:
— проверка статистической значимости коэффициентов уравнения регрессии.
— проверка общего качества уравнения регрессии;
— проверка свойств данных, выполнимость которых предполагалась при оценивании уравнения (проверка выполнимости предпосылок МНК).
Ведем понятие нулевая гипотеза. Нулевая гипотеза – это предположение о том, что две совокупности, рассматриваемые с точки зрения одного или нескольких признаков, одинаковы. При этом предполагается, что действительное значение равно нулю, а найденное из эксперимента отличие от нуля носит случайный характер.
Нулевые гипотезы проверяются с помощью статистичес ких критериев.
Поскольку статистические критерии могут установить только отличие, но не одинаковость совокупностей относительно рассматриваемых признаков, то нуль-гипотеза, как правило, выдвигается для проверки, нет ли оснований для ее отбрасывая и принятия альтернативной гипотезы.
Проверка достоверности коэффициентов модели произ водится с помощью статистического критерия Стьюдента.
Шаг 1. Выдвигается нулевая гипотеза
Шаг 2. Вычисляются ошибка коэффициента модели S i .
Шаг 3. Вычисляется фактическое значение критерия Стьюдента
Шаг 4. Затем находится табличное значение критерия Стьюдента, соответствующее уровню значимости и числу степеней свободы v = n – m – 1; t кр. = t /2; v .
Шаг 5. Сравниваются фактические значения критерия Стьюдента с его критическим значением t /2 .
Если | t | > t /2 ( = 0,05; m = n — k ), то нулевая гипотеза отвергается с вероятностью 1- и считается, что коэффи циент i достоверно отличается от нуля.
Если | t | t /2 ( = 0,05; m = n — k ), то нулевая гипотеза принимается и считается, что достоверность i статистичес ки не доказана.
Проверка достоверности модели производится с помощью статистического критерия Фишера.
Шаг 1. Выдвигается нулевая гипотеза
Н 0 : между рассматриваемыми переменными нет связи.
Шаг 2. Вычисляется фактическое значение критерия Фишера
F = S рег 2 / S ост 2
Шаг 3. Определяется критическое значение критерия Фишера на уровне значимости = 0,05, числе степеней сво боды m 1 и m 2 . Критическое значение критерия Фишера можно найти по таблицам, которые есть в каждом учебнике по эко нометрике.
Критическое значение критерия Фишера имеет следую щие параметры:
F к p ( = 0,05; m 1 = k — 1; m 2 = n — k ),
где — уровень значимости критерия;
m 1 — число степеней свободы для большей дисперсии регрессии;
m 2 — число степеней свободы для меньшей дисперсии остатков;
n — объем выборки;
к — количество всех коэффициентов модели.
Шаг 4. Сравниваются фактические значения критерия Фишера с его критическим значением.
Если F > F Kp F к p ( = 0,05; m 1 = k — 1; m 2 = n — k ), то нулевая гипотеза отвергается с вероятностью 1- и считает ся, что модель является достоверной.
Если F F к p ( = 0,05; m 1 = k — 1; m 2 = n — k ), то нулевая гипотеза принимается и считается, что достоверность модели не доказана, при этом не указывается вероят ность этого утверждения.
Предложенный критерий Фишера проверки достовер ности модели имеет существенный недостаток, который заключается в том, что он является внутренним критерием. При этом чем меньше ошибка модели, тем достовернее она становится. Это справедливо до того момента, когда модель описывает существующую тенденцию, при дальнейшем уменьшении ошибки модели уравнение регрессии будет проходить через случайные составляющие, что приведет к фактичес кому увеличению ошибки прогноза.
Наличие автокорреляции в модели устанавливается с помощью статистики Дарбина-Уотсона. Схема нахождения статистики Дарбина-Уотсона:
Шаг 1. Вычисляется критерий Дарбина – Уотсона
Шаг 2. Определяются по таблицам нижнее и верхнее пороговые значения соответственно d н и d в , зависящие от числа измерений, уровня значимости и числа объясняемых факторов в модели.
Шаг 3. Проверяются следующие условия:
1 ) если d в DW d в , то нулевая гипотеза об отсутствии автокорреляции принимается;
2 ) если d н DW d в или 4 – d в DW 4 – d н , то нулевая гипотеза об отсутствии автокорреляции не принимается и не отвергается (область неопределенности критерия);
3 ) если 0 DW d н , то нулевая гипотеза об отсутствии автокорреляции отвергается и утверждается, что имеется положительная автокорреляция остатков;
4 ) если 4 – d н DW
Так же наличие автокорреляции можно установить с помощью Q -статистики Льюинга-Бокса и теста на серийную автокорреляцию Бреуша-Годфрея.
Для проверки на наличие гетероскедастичности в модели можно воспользоваться рядом тестов, например тест Вайта, тест Парка и д. р. В нашем случае для проверки на гетероскедастичность мы будем пользоваться тестом Бреуша-Пагана.
Тест Бреуша — Пагана применяется в тех случаях, когда априорно предполагается, что дисперсии зависят от некоторых дополнительных переменных. Сначала проводится обычная (стандартная) регрессия и получается вектор остатков. Затем строится оценка дисперсии. Далее проводится регрессия квадрата вектора остатков деленного на эмпирическую дисперсию (оценку дисперсии). Для нее (регрессии) находят объясненную часть вариации. А для этой объясненной части вариации, деленной пополам, строится статистика. Если верна нулевая гипотеза (справедливо отсутствие гетероскедастичности), то эта величина имеет распределение χ 2 . Если же тест, напротив, выявил гетероскедастичность, то исходная модель преобразуется делением компонентов вектора остатков на соответствующие компоненты вектора наблюдаемых независимых переменных.
Тест У айта предполагает, что дисперсия ошибок регрессии представляет собой квадратичную функцию от значений факторов, например при наличии 2-х факторов:
ε 2 = a + b 1 x 1 + b 11 x 1 2 + b 2 x 2 + b 12 ∙x 1 ∙x 2 .
Так что модель включает в себя не только значения факторов, но и их квадраты, а так же попарные произведения. Поскольку каждый параметр модели ε i 2 = f ( x i ) должен быть рассчитан на основе достаточного числа степеней свободы то чем меньше объем исследуемой совокупности, тем в меньшей мере квадратичная функция сможет содержать попарные произведения факторов.
В настоящее время тест Уайта включен стандартную программу регрессионного анализа в пакете « Gretl ». О наличии или отсутствии гетероскеда ности остатков судят по величине F -критерия Фишера для квадратичной функции регрессии остатков. Если фактическое значение F -критерия выше табличного, то, следовательно, существует четкая корреляционная связь дисперсии ошибок от значений факторов, включенных в регрес сию, и имеет место гетероскедас тичность остатков. В противном случае ( F факт F табл ) делается вывод об отсутствии гетероскедастичности остатков регрессии.
Значения исходных данных представлены в таблице 1.
🔥 Видео
Математика без Ху!ни. Метод Гаусса. Совместность системы. Ранг матрицы.Скачать

Решение систем уравнений. Методом подстановки. Выразить YСкачать

15. Однородная система линейных уравнений / фундаментальная система решенийСкачать

Матричный метод решения систем уравненийСкачать

Решение систем уравнений методом подстановкиСкачать

Решение тригонометрических уравнений и их систем. 10 класс.Скачать

Эконометрика в Gretl, временные ряды.Скачать

Базисные решения систем линейных уравнений (03)Скачать

Построение модели множественной регрессии в программе GretlСкачать

Метод Крамера за 3 минуты. Решение системы линейных уравнений - bezbotvyСкачать

Решение системы линейных уравнений с двумя переменными способом подстановки. 6 класс.Скачать

ЛЕКЦИЯ 1.2. Определитель ВронскогоСкачать

Эконометрика. Линейная парная регрессияСкачать

Системы эконометрических уравненийСкачать

Лекция 13. Исследование систем линейных уравнений. Теорема Кронекера — Капелли.Скачать

Однородное уравнение в системеСкачать

Эконометрия_л9Скачать