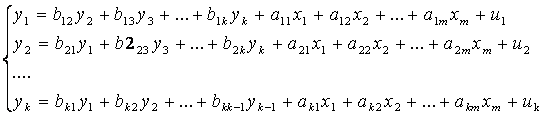Система одновременных уравнений модель спроса и предложения

Линейная регрессионная модель

Пусть определен характер экспериментальных данных и выделен определенный набор объясняющих переменных. Для того, чтобы найти объясненную часть, т. е. величину

Л/д-( У), требуется знание условных распределений случайной величины К. На практике это почти никогда не имеет места, поэтому точное нахождение объясненной части невозможно. В таких случаях применяется стандартная процедура сглаживания экспериментальных данных, подробно описанная.

Эта процедура состоит из двух этапов:

1) определяется параметрическое семейство, к которому принадлежит искомая функция Mx(Y) (рассматриваемая как функция от значений объясняющих переменных X).

Это может быть множество линейных функций, показа­тельных функций и т.д.;

2) находятся оценки параметров этой функции с помощью одного из методов математической статистики. Формально никаких способов выбора параметрического семейства не существует. Однако в подавляющем большинстве случаев эконометрические модели выбираются линейными .

Кроме вполне очевидного преимущества линейной модели

ее относительной простоты, — для такого выбора имеются, по крайней мере, две существенные причины.

Первая причина: если случайная величина (X, Y) имеет совместное нормальное распределение, то, как известно, уравнения регрессии линейные. Предположение о нормальном распределении является вполне естественным и в ряде случаев может быть обосновано с помощью предельных теорем теории вероятностей.

В других случаях сами величины Y или X могут не иметь нормального распределения, но некоторые функции от них распределены нормально. Например, известно, что логарифм доходов населения — нормально распределенная случайная величина. Вполне естественно считать нормально распределенной случайной величиной пробег автомобиля. Часто гипотеза о нормальном распределении принимается во многих случаях, когда нет явного ей противоречия, и, как показывает практика, подобная предпосылка оказывается вполне разумной.

Вторая причина, по которой линейная регрессионная модель оказывается предпочтительнее других, — это меньший риск значительной ошибки прогноза.

Система одновременных уравнений (модель спроса и предложения)

Особенностью этих систем является то, что каждое из уравнений системы, кроме «своих» объясняющих переменных, может включать объясняемые переменные из других уравнений. Таким образом в отличие от регрессионных уравнений тождества не содержат подлежащих оценке параметров модели и не включают случайной составляющей.

Таким образом, мы имеем не одну зависимую переменную, а набор зависимых (объясняемых) переменных, связанных уравнениями системы. Такую систему называют также системой одновременных уравнений, подчеркивая тот факт, что в системе одни и те же переменные одновременно рассматриваются как зависимые в одних уравнениях и независимые в других.

Системы одновременных уравнений наиболее полно описывают экономический объект, содержащий множество взаимосвязанных эндогенных (формирующихся внутри функционирования объекта) и экзогенных (задаваемых извне) переменных. При этом в качестве эндогенных и экзогенных могут выступать лаговые (взятые в предыдущий момент времени) переменные.

Классическим примером такой системы является модель спроса Q и предложения Q, когда спрос на товар определятся его ценой Р и доходом потребителя /, предложение

товара — его ценой Р и достигается равновесие между спросом и предложением:

в этой системе экзогенной переменной выступает доход потребителя, а эндогенными — спрос (предложение) товара Qd =Qs =Q и цена товара (цена равновесия) Р.

В другой модели спроса и предложения в качестве объясняющей предложение Qf переменной может быть не только цена товара Р в данный момент времени, т.е. Д но и цена товара в предыдущий момент времени — т.е. лаговая эндогенная переменная:

Обобщая изложенное, можно сказать, что эконометрическая модель позволяет объяснить поведение эндогенных переменных в зависимости от значений экзогенных и лаговых эндогенных переменных (иначе — в зависимости от предопределенных, т.е. заранее определенных, переменных).

Завершая рассмотрение понятия эконометрической модели, следует отметить следующее. Не всякая экономико-математическая модель, представляющая математико-статистическое описание исследуемого экономического объекта, может считаться эконометрической. Она становится эконометрической только в том 20 случае, если будет отражать этот объект на основе характеризующих именно его эмпирических <статистических) данных.

1. Основные этапы эконометрического моделирования. Проблемы эконометрического
   моделирования.

Можно выделить шесть основных этапов эконометрического моделирования: постановочный, априорный, этап параметризации, информационный, этапы идентификации и верификации модели.

1-й этап <постановочный). Формируется цель исследования, набор участвующих в модели экономических переменных. В качестве цели эконометрического моделирования обычно рассматривают анализ исследуемого экономического объекта (процесса); прогноз его экономических показателей, имитацию развития объекта при различных значениях экзогенных переменных (отражая их случайный характер, изменение во времени), выработку управленческих решений.

При выборе экономических переменных необходимо теоретическое обоснование каждой переменной (при этом рекомендуется, чтобы число их было не очень большим и, как минимум, в несколько раз меньше числа наблюдений). Объясняющие переменные не должны быть связаны функциональной или тесной корреляционной зависимостью, так как это может привести к невозможности оценки параметров модели или к получению неустойчивых, не имеющим реального смысла оценок, т.е. ктявлению мультиколлинеарности.

2-й этап <априорный). Проводится анализ сущности изучаемого объекта, формирование и формализация априорной (известной до начала моделирования) информации.

3-й этап (параметризация). Осуществляется непосредственно моделирование, т.е. выбор общего вида модели, выявление входящих в нее связей.

4’й этап (информационный). Осуществляется сбор необходимой статистической информации — наблюдаемых значений экономических переменных. Здесь могут быть наблюдения, полученные как с участием исследователя, так и без его участия (в условиях активного или пассивного эксперимента),

5-й этап (идентификация модели). Осуществляется статистический анализ модели и оценка ее параметров. Реализации этого этапа посвящена основная часть учебника. С проблемой идентификации модели не следует путать проблему ее идентифицируемости, т. е. проблему возможности получения однозначно определенных параметров модели, заданной системой одновременных уравнений (точнее, параметров

структурной формы модели, раскрывающей механизм формирования значений эндогенных переменных, по параметрам приведенной формы модели, в которой эндогенные переменные непосредственно выражаются через предопределенные переменные).

6’й этап (верификация модели). Проводится проверка истинности, адекватности модели. Выясняется, насколько удачно решены проблемы спецификации, идентификации и идентифицируемости модели, какова точность расчетов по данной модели, в конечном счете, насколько соответствует построенная модель моделируемому реальному экономическому объекту или процессу.

Следует заметить, что если имеются статистические данные, характеризующие моделируемый экономический объект в данный и предшествующие моменты времени, то для верификации модели, построенной для прогноза, достаточно сравнить реальные значения переменных в последующие моменты времени с соответствующими их значениями, полученными на основе рассматриваемой модели по данным предшествующих моментов.

Приведенное выше разделение эконометрического моделирования на отдельные этапы носит в известной степени условный характер, так как эти этапы могут пересекаться, взаимно дополнять друг друга и т. п.

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.016 сек.)

Видео:Как спрос и предложение задают ценыСкачать

Системы эконометрических уравнений

Пример . Рассмотрим модель зависимости общей величины расходов на питание от располагаемого личного дохода (х) и цены продуктов питания (р):у = а₀ + а₁х + а₂р + ε. Определим класс модели и вид переменных модели: регрессионная модель с одним уравнением; эндогенная переменная — расходы на питание, экзогенные переменные — располагаемый личный доход и цена продуктов питания.

Принципиальные сложности применения систем эконометрических уравнений связаны с ошибками спецификации модели.

Система уравнений в эконометрических исследованиях может быть построена по-разному. Выделяют следующие 3 вида систем уравнений.

1. Система независимых уравнений, когда каждая зависимая переменная (y ) рассматривается как функция только от предопределенных переменных (х):
   
2. Система рекурсивных уравнений, когда в каждом последующем уравнении системы зависимая переменная представляет функцию от зависимых и предопределенных переменных предшествующих уравнений:

От структурной формы легко перейти к так называемой приведенной форме модели. Число уравнений в приведенной форме равно числу эндогенных переменных модели. В каждом уравнении приведенной формы эндогенная переменная выражается через все предопределенные переменные модели:

Так как правая часть каждого из уравнений приведенной формы содержит только предопределенные переменные и остатки, а левая часть только одну из эндогенных переменных, то такая система является системой независимых уравнений. Поэтому параметры каждого из уравнений системы в приведенной форме можно определить независимо обычным МНК.
Зная оценки этих приведенных коэффициентов можно определить параметры структурной формы модели. Но не всегда, а только если модель является идентифицируемой.

Видео:Равновесная цена | Крест МаршаллаСкачать

Проблема идентификации

Количество структурных и приведенных коэффициентов одинаково в модели идентифицируемой.

Видео:Эластичность спроса и предложения | Как цена влияет на спросСкачать

Правила идентификации

Ранг данной матрицы равен 1, что меньше К-1=2, следовательно, 1-ое уравнение модели неидентифицированно.
Составим матрицу А для 2-ого уравнения системы. Во 2-ом уравнении отсутствуют переменные y₃, x₂, х₃:
y₃ x ₂ x₃
b₁₃ a ₁₃ 0 — в 1-ом уравнении
1 a₃₂ a₃₃ — в 3-ем уравнении
Ранг данной матрицы равен 2, что равно К-1=2, следовательно, 2-ое уравнение модели точно идентифицированно.
Составим матрицу А для 3-его уравнения системы. В 3-ем уравнении отсутствуют переменные y₁, x₂:
y ₁ x ₂
1 a₁₂ — в 1-ом уравнении
b₂₁ 0 — во 2-ом уравнении
Ранг данной матрицы равен 1, что меньше К-1=2, следовательно, 3-е уравнение модели неидентифицированно.

Сделаем выводы: 1-ое и 3-е уравнения системы неидентифицированны (т.к. не выполняются достаточные условия идентификации, а в случае 1-ого уравнения и необходимое условие также). 2-ое уравнение системы сверхидентифицированно. Следовательно, система в целом является неидентифицируемой.
Для оценки параметров 2-ого уравнения можно применить двухшаговый МНК. Параметры 1-ого и 3-его уравнений определить по коэффициентам приведенной формы нельзя. Поэтому модель должна быть модифицирована.

Видео:Микра для начинающих/Эластичность_3Скачать

Применение систем уравнений для построения макроэкономических моделей и моделей спроса – предложения

Рис. 20. 3. Основные направления использования систем эконометрических уравнений

Статическая модель Кейнса:

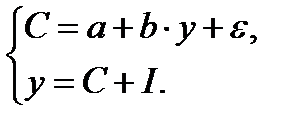
С – личное потребление в постоянных ценах;

y – национальный доход в постоянных ценах;

e — случайная составляющая;

I– инвестиции в постоянных ценах.

В силу наличия тождества в модели структурный коэффициент b не может быть больше 1. Он характеризует предельную склонность к потреблению. Если b>1, то y

Бокса-Кокса подход — формализованная процедура подбора линеаризующего преобразования.

Верификация модели – проверка истинности модели, определение соответствия построенной модели реальному экономическому явлению.

Внутренне линейная нелинейная модель с помощью преобразований может быть приведена к линейному виду.

Внутренне нелинейная модель не может быть сведена к линейной функции.

Временной ряд – совокупность значений какого-либо показателя за несколько последовательных моментов времени.

Выборочная совокупность – часть генеральной совокупности.

Генеральная совокупность — вся совокупность объектов исследования, объем выборки которой должен быть равен бесконечности.

Гетероскедастичность – неоднородность относительно дисперсии.

Голдфелда Квандта тест – один из наиболее распространенных способов тестирования остатков регрессии на гетероскедастичность.

Гомоскедастичность остатков регрессии – постоянство дисперсии случайных отклонений εi.

Дарбина-Уотсона тест – один из наиболее распространенных способов тестирования остатков регрессии на автокорреляцию

Двухшаговый метод наименьших квадратов — метод оценивания точно идентифицируемых и сверхидентифицируемых систем уравнений, который основан на конструировании новых значений эндогенных переменных по приведенной форме модели и замене эндогенных переменных в правой части каждого уравнения их прогнозными значениями.

Дискретная зависимая переменная – это переменная, которая принимает несколько альтернативных значений.

Дифференциальный коэффициент свободного члена – это коэффициент перед фиктивной переменной в регрессионной модели. Он показывает, на какую величину отличается свободный коэффициент а при значении D=1, от свободного коэффициента а при D=0.

Дифференциальный угловой коэффициент – это коэффициент перед произведением фиктивной переменной и независимой переменной в регрессионной модели. Он показывает, на какую величину отличается коэффициент регрессии b при значении D=1, от коэффициента регрессии b при D=0.

Достаточное условие идентификации – определитель матрицы, со-ставленный из коэффициентов при переменных, отсутствующих в иссле-дуемых уравнениях, не равен нулю, и ранг этой матрицы не менее числа эндогенных переменных системы без единицы. Для решения идентифици-руемого уравнения применяется косвенный МНК, для решения сверхидентифицируемого – двухшаговый МНК.

Идентификация модели – проведение статистического анализа моде-ли и оценивания качества ее параметров.

Индекс корреляции – показатель тесноты статистической взаимосвязи, выраженной в нелинейной форме.

Индекс множественной корреляции оценивает тесноту совместного влияния факторов на результативный признак Y.

Интервальный прогноз — интервал, в котором с определенной вероятностью находится фактическое значение прогнозной переменной экономического объекта.

Коллинеарными называются две переменные, которые находятся между собой в линейной зависимости

Коррелограмма – график зависимости значений автокорреляционной функции временного ряда от величины лага.

Корреляция – это статистическая зависимость между случайнымиве-личинами, при которой изменение одной из случайных величин приводит к изменению математического ожидания другой.

Косвенный метод наименьших квадратов – метод оценивания точно идентифицируемых систем уравнений, который основан на вычислении оценок структурных параметров через решение системы нелинейных уравнений, связывающих приведенные и структурные коэффициенты.

Коэффициент детерминации – это показатель, который определяет долю разброса зависимой переменной Y, объясняемую регрессией Y на X.

Коэффициент корреляции — числовая характеристика совместного распределения двух случайных величин, выражающая их взаимосвязь.

Коэффициент эластичности – показатель, который измеряет, на сколько процентов изменится результативный признак Y, если факторный признак изменится на 1 %.

Лаг – число периодов, по которым рассчитывается коэффициент корреляции временного ряда.

Линеаризация – приведение нелинейных моделей регрессии к линейному виду путем замены, логарифмирования переменных или комбинированным способом с целью применения МНК.

Линейный коэффициент парной корреляции – это показатель тесноты статистической взаимосвязи между переменными Y и X.

Ловушка фиктивной переменной – это состояние совершенной мультиколлинеарности в силу строгой линейной зависимости между переменными D1 и D2, при котором коэффициенты уравнения регрессии однозначно определены быть не могут.

Логит-модель основана на использовании функции логистического распределения.

Метод максимального правдоподобия – один из способов оценивания параметров регрессии, в частности, в моделях с дискретной зависимой переменной.

Метод наименьших квадратов – один из распространенных способов оценивания параметров регрессии.

Множественная корреляция – это зависимость между результативным признаком и двумя и более факторными признаками.

Множественная регрессия представляет собой модель, где теорети-ческое (среднее) значение зависимой переменной Y рассматривается как функция нескольких независимых переменных X1, X2. Xm.

Модели бинарного выбора содержат зависимую переменную, которая принимает лишь два альтернативных значения, обозначаемых цифровыми метками: 0 и 1.

Модель авторегрессии – скользящего среднего – это линейная модель множественной регрессии, в которой в качестве объясняющих переменных выступают прошлые значения самой зависимой переменной, а в качестве регрессионного остатка – скользящие средние из элементов «белого шума».

Модель временного ряда – разновидность эконометрической модели, в которой результативный признак является функцией переменной времени или переменных, относящихся к другим моментам времени.

Мультиколлинеарность — это линейная взаимосвязь двух или не-скольких объясняющих переменных (х1, х2, … хm).

Мультипликативная модель временного ряда – временной ряд представлен как произведение циклической, трендовой, случайной компонент.

Неидентифицирyемая модель — разновидность структурной модели системы одновременных уравнений, в которой структурные коэффициенты невозможно найти по приведенным коэффициентам. 105

Нелинейная регрессия внутренне линейная, т.е. она с помощью соответствующих преобразований может быть приведена к линейному виду

Нелинейная регрессия внутренне нелинейная, т.е. она не может быть сведена к линейной функции.

Необходимое условие идентификации — выполнение счетного правила:D+1=H – уравнение идентифицируемо, D+1 H – уравнение сверхидентифицируемо (Н – число эндогенных переменных в уравнении, D – число предопределенных переменных, отсутствующих в уравнении, но присутствующих в системе).

Объект эконометрики — экономические процессы, происходящие в экономической системе общества.

Объясняющая переменная (причина, независимая переменная, объясняющий фактор)-это характеристика объекта, которая вызывает следствие у зависимой переменной .

Параметризация модели – выражение в математической форме взаимосвязи между переменными модели, формулирование исходных предпосылок и ограничений модели.

Парная регрессия представляет собой модель, где теоретическое (среднее) значение зависимой переменной Y рассматривается как функция одной независимой переменной X.

Парный коэффициент регрессии показывает, на какую величину в среднем изменится результативный признак Y, если переменную X увели-чить на единицу измерения.

Предмет эконометрики — количественная оценка взаимосвязи между случайными событиями, признаками, показателями, факторами переменных экономических объектов.

Предопределенные переменные – это экзогенные переменные и лаго-вые эндогенные переменные.

Приведенная система одновременных уравнений – система уравнений, которая отражает зависимость эндогенных переменных только от экзогенных переменных.

Приведенная форма модели — система линейных функций эндогенных переменных от всех предопределенных переменных системы.

Пробит-модельоснована на использовании функции стандартного нормального распределения.

Прогноз — предвидение, предсказание. Различают два вида: точечный и интервальный прогноз.

Регрессионный анализ — раздел аналитической статистики, изучающий форму зависимости характеристик стохастического процесса от одного или нескольких факторов.

Сверхидентифицируемая модель — разновидность структурной модели системы одновременных уравнений, в которой структурные коэффициен-ты, выраженные через приведенные коэффициенты, имеют два и более числовых значений.

Сезонная компонента – компонента временного ряда, которая харак-теризуетвнутригодичные колебания показателя. В общем виде является циклической составляющей.

Сезонные колебания – это колебания, периодически повторяющиеся в некоторое определенное время каждого года, месяца, дня или его часа.

Система взаимосвязaнных уравнений – одни и те же зависимые переменные в одних уравнениях входят в левую часть, а в других – в правую.

Система независимых уравнений – каждая зависимая переменная у рассматривается как функция одного и того же набора факторов х.

Система рекурсивных уравнений – зависимая переменная у одного уравнения выступает в виде фактора х в другом уравнении.

Спецификация модели — формулирование вида модели, исходя из со-ответствующей теории связи между переменными.

Стохастический — случайный, вероятностный.

Структурная форма модели – система взаимосвязных (совместных) уравнений, в которой одни и те же зависимые переменные в одних уравнениях входят в левую часть, а в других – в правую.

Тенденция — направление, в котором совершается развитие какого-либо явления.

Тобит-модель – модель для описания зависимости цензурированной зависимой переменной от влияющих на нее факторов.

Точечный прогноз — среднее прогнозное значение изучаемой переменной экономического объекта.

Тренд – это основная достаточно устойчивая тенденция во временном ряду, более или менее свободная от случайных колебаний.

Трехшаговый метод наименьших квадратов — метод оценивания точно идентифицируемых и сверхидентифицируемых систем, который основан на анализе ковариационной матрицы ошибок с использованием оценок, полученных в результате применения двухшагового метода наименьших квадратов.

Фиктивные переменные — качественные переменные, преобразован-ныев количественные с помощью цифровых меток.

Цель регрессионного анализа – оценка функциональной зависимости между независимыми переменными X и условным математическим ожиданием зависимой переменной Y.

Цель эконометрики – эмпирический (практический) вывод экономических законов.

Циклические (или периодические ) колебания состоят в том, что значение изучаемого признака в течение какого-то времени возрастает, достигая определенного максимума, затем понижается, достигая определенного минимума, вновь возрастает до прежнего значения и т.д.

Частное уравнение регрессии характеризует изолированное влияние фактора Xj на результат.

Частные уравнения регрессии — уравнения регрессии, которые связывают результативный признак с соответствующими факторами при закреплении других учитываемых во множественной регрессии факторов на среднем уровне

Частный коэффициент эластичности показывает, на сколько % из-меняется в среднем результативный признак Y при изменении фактора Xj на 1%.

Чоу тест – это статистический тест, определяющий целесообразность использования фиктивной переменной.

Экзогенные переменные – независимые переменные, которые опреде-ляются вне системы.

Эконометрика – это наука, которая дает количественное выражение взаимосвязей экономических явлений и процессов, которые раскрыты и обоснованы экономической теорией.

Экстраполяция — прогноз, получение расчетных значений при условии.что значения аргумента выходят за пределы области определения функции.

Эндогенные переменные — это переменные, значение которых определяются внутри модели и обозначаются обычно как у.

📹 Видео

Лекция 1. Формирование равновесной цены. Общее равновесие. Эффективность по ПаретоСкачать

2.3 Рыночное равновесиеСкачать

Система уравнений с двумя эндогенными переменнымиСкачать

2.1 Спрос и величина спросаСкачать

Решение систем уравнений методом подстановкиСкачать

Макроэкономика. Совместное равновесие товарного и денежного рынков Модель IS-LM.Скачать

7inR 2. Instrumental Variables and Simultaneous Equations ModelsСкачать

Макроэкономика. Особенности спроса и предложения денег.Скачать

Микра для начинающих/ЭД и ЭЗ. Модель СлуцкогоСкачать

Теория автоматического регулирования. Лекция 5. Модели параметров состоянийСкачать

Кейнсианская экономикаСкачать

Урок - 3# - Взаимодействие спроса и предложения. Равновесие на рынкеСкачать

9 класс, 14 урок, Системы уравнений как математические модели реальных ситуацийСкачать

7inR 9. Structural models with testable identification (in Russian).Скачать

Как решать уравнения с модулем или Математический торт с кремом (часть 1) | МатематикаСкачать

7 класс, 40 урок, Системы двух линейных уравнений с двумя переменными как математические моделиСкачать