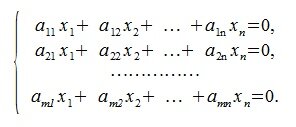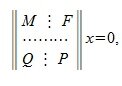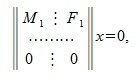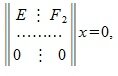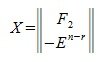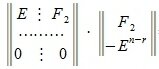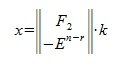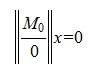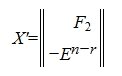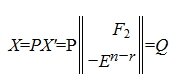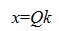Система однородных линейных алгебраических уравнений всегда имеет решения отличные от нулевого если (3 видео)

Однородные системы линейных алгебраических уравнений. Фундаментальная система решений. Первая часть.

Содержание

Однородные системы линейных алгебраических уравнений. Нулевое (тривиальное) решение.
Фундаментальная система решений однородной СЛАУ.
Система однородных линейных алгебраических уравнений всегда имеет решения отличные от нулевого если
Однородная система линейных уравнений
Обшее решение однородной системы линейных уравнений
Нахождение общего решения однородной системы линейных уравнений с помощью псевдообратной матрицы
Решение однородной системы линейных уравнений онлайн
🎬 Видео

Видео:15. Однородная система линейных уравнений / фундаментальная система решенийСкачать

Однородные системы линейных алгебраических уравнений. Нулевое (тривиальное) решение.

Для начала стоит вспомнить, что такое однородные системы линейных алгебраических уравнений. В теме «Система линейных алгебраических уравнений. Основные термины. Матричная форма записи» вопрос классификации систем осуществлялся подробно, здесь же лишь вкратце напомню основные термины. Итак, система линейных алгебраических уравнений (СЛАУ) называется однородной, если все свободные члены этой системы равны нулю. Например, система $left < begin& 2x_1-3x_2-x_3-x_4=0;\ & -4x_1+5x_2+3x_4=0. end right.$ является однородной, так как все свободные члены этой системы (т.е. числа, стоящие в правых частях равенств) – нули.

Любая однородная СЛАУ имеет хотя бы одно решение – нулевое (его ещё называют тривиальное), в котором все переменные равны нулю. Подставим, например, $x_1=0$, $x_2=0$, $x_3=0$ и $x_4=0$ в записанную выше систему. Получим два верных равенства:

Однако следствие из теоремы Кронекера-Капелли однозначно указывает на то, что если СЛАУ имеет решение, то есть только два варианта. Либо это решение единственно (и тогда СЛАУ называют определённой), либо этих решений бесконечно много (такую СЛАУ именуют неопределённой). Возникает первый вопрос: как выяснить, сколько решений имеет заданная нам однородная СЛАУ? Одно (нулевое) или бесконечность?

Та однородная СЛАУ, которая рассмотрена выше, имеет не только нулевое решение. Подставим, например, $x_1=1$, $x_2=-1$, $x_3=2$ и $x_4=3$:

Мы получили два верных равенства, поэтому $x_1=1$, $x_2=-1$, $x_3=2$, $x_4=3$ – тоже является решением данной СЛАУ. Отсюда, кстати, следует вывод: так как наша СЛАУ имеет более чем одно решение, то эта СЛАУ является неопределенной, т.е. она имеет бесконечное количество решений.

Кстати сказать, чтобы не писать каждый раз выражения вроде «$x_1=1$, $x_2=-1$, $x_3=2$, $x_4=3$», пишут все значения переменных в матрицу-столбец: $left(begin 1 \ -1 \ 2 \ 3 end right)$. Эту матрицу тоже называют решением СЛАУ.

Теперь можно вернуться к вопросу о количестве решений однородной СЛАУ. Согласно следствию из теоремы Кронекера-Капелли, если $r=n$ ($n$ – количество переменных), то СЛАУ имеет единственное решение. Если же $r < n$, то СЛАУ имеет бесконечное количество решений.

Случай $r=n$ не интересен. Для однородных СЛАУ он означает, что система имеет только нулевое решение. А вот случай $r < n$ представляет особый интерес.

Этот случай уже был рассмотрен в теме «Базисные и свободные переменные. Общее и базисное решения СЛАУ». По сути, однородные СЛАУ – это всего лишь частный случай системы линейных уравнений, поэтому вся терминология (базисные, свободные переменные и т.д.) остаётся в силе.

Что такое базисные и свободные переменные? показатьскрыть

Прежде чем дать определение этим терминам, стоит вспомнить, что означает фраза «ранг матрицы равен $r$». Она означает, что есть хотя бы один минор $r$-го порядка, который не равен нулю. Напомню, что такой минор называется базисным. Базисных миноров может быть несколько. При этом все миноры, порядок которых выше $r$, равны нулю или не существуют. Теперь можно дать следующее определение:

Выбрать $r$ базисных переменных в общем случае можно различными способами. В примерах я покажу наиболее часто используемый способ выбора.

Видео:Видеоурок "Однородные системы линейных уравнений"Скачать

Фундаментальная система решений однородной СЛАУ.

С однородными СЛАУ связано дополнительное понятие – фундаментальная система решений. Дело в том, что если ранг матрицы системы однородной СЛАУ равен $r$, то такая СЛАУ имеет $n-r$ линейно независимых решений: $varphi_1$, $varphi_2$. $varphi_$.

Часто вместо словосочетания «фундаментальная система решений» используют аббревиатуру «ФСР». Если решения $varphi_1$, $varphi_2$. $varphi_$ образуют ФСР, и $X$ – матрица переменных данной СЛАУ, то общее решение СЛАУ можно представить в таком виде:

$$ X=C_1cdot varphi_1+C_2cdot varphi_2+ldots+C_cdot varphi_, $$

где $C_1$, $C_2$. $C_$ – произвольные постоянные.

Что значит «линейно независимые решения»? показатьскрыть

В данной ситуации под решением понимается матрица-столбец, в которой перечислены значения неизвестных.

Решения $varphi_1$, $varphi_2$, $ldots$, $varphi_n$ называются линейно зависимыми, если существуют такие константы $alpha_1,;alpha_2,;alpha_3,ldots,alpha_n$, что выполняется следующее равенство:

$$ alpha_1cdot varphi_1+alpha_2cdot varphi_2+ldots+alpha_ncdot varphi_n=O $$

при условии, что среди коэффициентов $alpha_i$ есть хотя бы один, не равный нулю.

Если же указанное выше равенство возможно лишь при условии $alpha_1=alpha_2=ldots=alpha_n=0$, то система решений называется линейно независимой.

Буква «$O$» в данном определении обозначает нулевую матрицу. Проще всего пояснить это определение на конкретном примере. Давайте рассмотрим ту СЛАУ, о которой шла речь в начале темы. Мы уже проверили, что $varphi_1=left(begin 1 \-1 \2 \3 endright)$ – решение данной СЛАУ. Точно так же можно показать, что $varphi_2=left(begin 16 \ 11 \ -4 \ 3 endright)$, $varphi_3=left(begin -5 \ -4 \ 2 \ 0 endright)$, $varphi_4=left(begin 7 \ 5 \ -2 \ 1endright)$ – решения данной системы.

Примем $alpha_1=-1$, $alpha_2=0$, $alpha_3=4$, $alpha_4=3$. Выясним, чему же равно выражение $alpha_1cdot varphi_1+alpha_2cdot varphi_2+alpha_3cdot varphi_3+alpha_4cdot varphi_4$:

$$ alpha_1cdot varphi_1+alpha_2cdot varphi_2+alpha_3cdot varphi_3+alpha_4cdot varphi_4= -1cdot left(begin 1 \-1 \2 \3 endright)+ 0cdot left(begin 16 \ 11 \ -4 \ 3 endright)+ 4cdot left(begin -5 \ -4 \ 2 \ 0 endright)+ 3cdot left(begin 7 \ 5 \ -2 \ 1endright)=\ =left(begin -1+0-20+21\ 1+0-16+15 \ -2+0+8-6 \ -3+0+0+3endright)= left(begin 0\ 0\ 0\0endright). $$

Итак, существуют такие значения констант $alpha_1$, $alpha_2$, $alpha_3$, $alpha_4$, не все одновременно равные нулю, что выполняется равенство $alpha_1cdot varphi_1+alpha_2cdot varphi_2+alpha_3cdot varphi_3+alpha_4cdot varphi_4=O$. Вывод: совокупность решений $varphi_1$, $varphi_2$, $varphi_3$, $varphi_4$ – линейно зависима.

Для сравнения: равенство $alpha_1cdot varphi_1+alpha_2cdot varphi_2=O$ возможно лишь при условии $alpha_1=alpha_2=0$ (я не буду это доказывать, поверьте на слово 🙂 ). Следовательно, система $varphi_1$, $varphi_2$ является линейно независимой.

Если система является неопределённой, указать фундаментальную систему решений.

Итак, мы имеем однородную СЛАУ, у которой 3 уравнения и 4 переменных: $x_1$, $x_2$, $x_3$, $x_4$. Так как количество переменных больше количества уравнений, то такая однородная система не может иметь единственное решение (чуть позже мы строго докажем это предложение на основе теоремы Кронекера-Капелли). Найдём решения СЛАУ, используя метод Гаусса:

$$ left( begin 3 & -6 & 9 & 13 & 0 \ -1 & 2 & 1 & 1 & 0 \ 1 & -2 & 2 & 3 & 0 end right) rightarrow left|begin & text\ & text\ & text endright| rightarrow \ rightarrowleft( begin 1 & -2 & 2 & 3 & 0\ -1 & 2 & 1 & 1 & 0 \ 3 & -6 & 9 & 13 & 0 end right) begin phantom \ II+I\ III-3cdot Iend rightarrow left( begin 1 & -2 & 2 & 3 & 0\ 0 & 0 & 3 & 4 & 0 \ 0 & 0 & 3 & 4 & 0 endright) begin phantom \ phantom\ III-IIend rightarrow \ rightarrowleft( begin 1 & -2 & 2 & 3 & 0\ 0 & 0 & 3 & 4 & 0 \ 0 & 0 & 0 & 0 & 0 endright). $$

Мы завершили прямой ход метода Гаусса, приведя расширенную матрицу системы к ступенчатому виду. Слева от черты расположены элементы преобразованной матрицы системы, которую мы также привели к ступенчатому виду. Напомню, что если некая матрица приведена к ступенчатому виду, то её ранг равен количеству ненулевых строк.

И матрица системы, и расширенная матрица системы после эквивалентных преобразований приведены к ступенчатому виду; они содержат по две ненулевых строки. Вывод: $rang A=rangwidetilde = 2$.

Итак, заданная СЛАУ содержит 4 переменных (обозначим их количество как $n$, т.е. $n=4$). Кроме того, ранги матрицы системы и расширенной матрицы системы равны между собой и равны числу $r=2$. Так как $r < n$, то согласно следствию из теоремы Кронекера-Капелли СЛАУ является неопределённой (имеет бесконечное количество решений).

Найдём эти решения. Для начала выберем базисные переменные. Их количество должно равняться $r$, т.е. в нашем случае имеем две базисные переменные. Какие именно переменные (ведь у нас их 4 штуки) принять в качестве базисных? Обычно в качестве базисных переменных берут те переменные, которые расположены на первых местах в ненулевых строках преобразованной матрицы системы, т.е. на «ступеньках». Что это за «ступеньки» показано на рисунке:

На «ступеньках» стоят числа из столбцов №1 и №3. Первый столбец соответствует переменной $x_1$, а третий столбец соответствует переменной $x_3$. Именно переменные $x_1$ и $x_3$ примем в качестве базисных.

В принципе, если вас интересует именно методика решения таких систем, то можно пропускать нижеследующее примечание и читать далее. Если вы хотите выяснить, почему можно в качестве базисных взять именно эти переменные, и нельзя ли выбрать иные – прошу раскрыть примечание.

Почему можно принять переменные $x_1$ и $x_3$ в качестве базисных? Для ответа на этот вопрос давайте вспомним, что ранг матрицы системы равен числу $r=2$. Это говорит о том, что все миноры данной матрицы, порядок которых выше 2, либо равны нулю, либо не существуют. Ненулевые миноры есть только среди миноров второго порядка. Выберем какой-либо ненулевой минор второго порядка. Мы можем выбирать его как в исходной матрице системы $A$, т.е. в матрице $left( begin 3 & -6 & 9 & 13 \ -1 & 2 & 1 & 1 \ 1 & -2 & 2 & 3 end right)$, так и в преобразованной матрице системы, т.е. в $left( begin 1 & -2 & 2 & 3 \ 0 & 0 & 3 & 4 \ 0 & 0 & 0 & 0 endright)$. Так как в преобразованной матрице системы побольше нулей, то будем работать именно с нею.

Итак, давайте выберем минор второго порядка, элементы которого находятся на пересечении строк №1 и №2, и столбцов №1 и №2:

$$ M_^=left| begin 1 & -2 \ 0 & 0 endright|=1cdot 0-(-2)cdot 0=0. $$

Вывод: выбранный нами минор второго порядка не является базисным, ибо он равен нулю. Так как элементы этого минора взяты из столбца №1 (он соответствует переменной $x_1$) и столбца №2 (он соответствует переменной $x_2$), то пара переменных $x_1$ и $x_2$ не могут быть базисными переменными.

Осуществим вторую попытку, взяв минор второго порядка, элементы которого лежат на пересечении строк №1, №2 и столбцов №2 и №4:

$$ M_^=left| begin 2 & 3\ 3 & 4 endright|=2cdot 4-3cdot 3=-1. $$

Вывод: выбранный нами минор второго порядка является базисным, ибо он не равен нулю. Так как элементы этого минора взяты из столбца №2 (он соответствует переменной $x_2$) и столбца №4 (он соответствует переменной $x_4$), то пару переменных $x_2$ и $x_4$ можно принять в качестве базисных.

Сделаем и третью попытку, найдя значение минора, элементы которого расположены на пересечении строк №1, №2 и столбцов №1 и №3:

Вывод: выбранный нами минор второго порядка является базисным, ибо он не равен нулю. Так как элементы этого минора взяты из столбца №1 (он соответствует переменной $x_1$) и столбца №3 (он соответствует переменной $x_3$), то пару переменных $x_1$ и $x_3$ можно принять в качестве базисных.

Как видите, выбор базисных переменных не является однозначным. На самом деле количество вариантов выбора не превышает количество размещений из $n$ элементов по $r$, т.е. не больше чем $C_^$.

В рассматриваемом примере в качестве баисных были приняты переменные $x_1$ и $x_3$ – сугубо из соображений удобства дальнейшего решения. В чём это удобство состоит, будет видно чуток позже.

Базисные переменные выбраны: это $x_1$ и $x_3$. Количество свободных переменных, как и количество решений в ФСР, равно $n-r=2$. Свободными переменными будут $x_2$ и $x_4$. Нам нужно выразить базисные переменные через свободные.

Я предпочитаю работать с системой в матричной форме записи. Для начала очистим полученную матрицу $left( begin 1 & -2 & 2 & 3 & 0\ 0 & 0 & 3 & 4 & 0 \ 0 & 0 & 0 & 0 & 0 endright)$ от нулевой строки:

$$ left( begin 1 & -2 & 2 & 3 & 0\ 0 & 0 & 3 & 4 & 0 endright) $$

Свободным переменным, т.е. $x_2$ и $x_4$, соответствуют столбцы №2 и №4. Перенесём эти столбцы за черту. Знак всех элементов переносимых столбцов изменится на противоположный:

Почему меняются знаки? Что вообще значит это перенесение столбцов? показатьскрыть

Давайте обратимся к расширенной матрице системы, которая после преобразований имеет вид $left( begin 1 & -2 & 2 & 3 & 0\ 0 & 0 & 3 & 4 & 0 endright)$. Перейдём от матрицы к уравнениям. Первая строка соответствует уравнению $x_1-2x_2+2x_3+3x_4=0$, а вторая строка соответствует уравнению $3x_3+4x_4=0$. Теперь перенесём свободные переменные $x_2$ и $x_4$ в правые части уравнений. Естественно, что когда мы переносим выражение $4x_4$ в правую часть уравнения, то знак его изменится на противоположный, и в правой части появится $-4x_4$.

Если опять записать полученную систему в виде матрицы, то мы и получим матрицу с перенесёнными за черту столбцами.

А теперь продолжим решение обычным методом Гаусса. Наша цель: сделать матрицу до черты единичной. Для начала разделим вторую строку на 3, а потом продолжим преобразования обратного хода метода Гаусса:

$$ left( begin 1 & 2 & 2 & -3\ 0 & 3 & 0 & -4 endright) begin phantom \ II:3 end rightarrow left( begin 1 & 2 & 2 & -3\ 0 & 1 & 0 & -4/3 endright) begin I-2cdot II \ phantom end rightarrow \ rightarrow left(begin 1 & 0 & 2 & -1/3\ 0 & 1 & 0 & -4/3 endright). $$

Матрица до черты стала единичной, метод Гаусса завершён. Общее решение найдено, осталось лишь записать его. Вспоминая, что четвёртый столбец соответствует переменной $x_2$, а пятый столбец – переменной $x_4$, получим:

Нами найдено общее решение заданной однородной СЛАУ. Если есть желание, то полученное решение можно проверить. Например, подставляя $x_1=2x_2-fracx_4$ и $x_3=-fracx_4$ в левую часть первого уравнения, получим:

$$ 3x_1-6x_2+9x_3+13x_4=3cdot left(2x_2-fracx_4right)-6x_2+9cdot left(-fracx_4right)+13x_4=0. $$

Проверка первого уравнения увенчалась успехом; точно так же можно проверить второе и третье уравнения.

Теперь найдем фундаментальную систему решений. ФСР будет содержать $n-r=2$ решения. Для нахождения ФСР составим таблицу. В первой строке таблицы будут перечислены переменные: сначала базисные $x_1$, $x_3$, а затем свободные $x_2$ и $x_4$. Всего в таблице будут три строки. Так как у нас 2 свободные переменные, то под свободными переменными запишем единичную матрицу второго порядка, т.е. $left(begin 1 & 0 \0 & 1endright)$. Таблица будет выглядеть так:

Теперь будем заполнять свободные ячейки. Начнём со второй строки. Мы знаем, что $x_1=2x_2-fracx_4$ и $x_3=-fracx_4$. Если $x_2=1$, $x_4=0$, то:

Найденные значения $x_1=2$ и $x_3=0$ запишем в соответствующие пустые ячейки второй строки:

Заполним и третью строку. Если $x_2=0$, $x_4=1$, то:

Найденные значения $x_1=-frac$ и $x_3=-frac$ запишем в соответствующие пустые ячейки третьей строки. Таким образом таблица будет заполнена полностью:

Из второй и третьей строки таблицы мы и запишем ФСР. Матрица неизвестных для нашей системы такова: $X=left(begin x_1 \x_2 \x_3 \x_4 endright)$. В том же порядке, в котором в матрице $X$ перечислены переменные, записываем значения переменных из таблицы в две матрицы:

$$ varphi_1=left(begin 2 \1 \0 \0 endright);; varphi_2=left(begin -1/3 \0 \ -4/3 \1 endright). $$

Совокупность $varphi_1=left(begin 2 \1 \0 \0 endright)$, $varphi_2=left(begin -1/3 \0 \ -4/3 \1 endright)$ и есть ФСР данной системы. Общее решение можно записать теперь так: $X=C_1cdot varphi_1+C_2cdot varphi_2$. Или в развёрнутом виде:

$$ X=C_1cdotleft(begin 2 \1 \0 \0 endright)+C_2cdotleft(begin -1/3 \0 \ -4/3 \1 endright), $$

где $C_1$ и $C_2$ – произвольные постоянные.

Ответ: Общее решение: $left <begin& x_1=2x_2-fracx_4;\ & x_2in R;\ & x_3=-fracx_4;\ & x_4 in R. endright.$. Или так: $X=C_1cdotleft(begin 2 \1 \0 \0 endright)+C_2cdotleft(begin -1/3 \0 \ -4/3 \1 endright)$, где $C_1$ и $C_2$ – произвольные константы. Фундаментальная система решений: $varphi_1=left(begin 2 \1 \0 \0 endright)$, $varphi_2=left(begin -1/3 \0 \ -4/3 \1 endright)$.

Записать ФСР однородной СЛАУ

зная общее решение. Записать общее решение с помощью ФСР.

Общее решение уже было получено в теме «метод Крамера» (пример №4). Это решение таково:

Опираясь на предыдущий пример №1, попробуйте составить ФСР самостоятельно, а потом сверить с ответом.

Ранг матрицы системы $r=3$ (поэтому у нас три базисных переменных), количество переменных $n=5$. Количество свободных переменных и количество решений ФСР равно $n-r=2$.

Так же, как и в предыдущем примере, составим ФСР. При составлении учтём, что $x_1$, $x_2$, $x_3$ – базисные переменные, а $x_4$, $x_5$ – свободные переменные.

Совокупность $varphi_1=left(begin -17/19 \-15/19 \20/19 \1\0 endright)$, $varphi_2=left(begin 144/19 \ 41/19 \ -4/19\0\1 endright)$ и есть ФСР данной системы. Общее решение можно записать теперь так: $X=C_1cdot varphi_1+C_2cdot varphi_2$. Или в развёрнутом виде:

$$ X=C_1cdotleft(begin -17/19 \-15/19 \20/19 \1\0 endright)+C_2cdotleft(begin 144/19 \ 41/19 \ -4/19\0\1 endright), $$

где $C_1$ и $C_2$ – произвольные постоянные.

Ответ: Фундаментальная система решений: $varphi_1=left(begin -17/19 \-15/19 \20/19 \1\0 endright)$, $varphi_2=left(begin 144/19 \ 41/19 \ -4/19\0\1 endright)$. Общее решение: $X=C_1cdotleft(begin -17/19 \-15/19 \20/19 \1\0 endright)+C_2cdotleft(begin 144/19 \ 41/19 \ -4/19\0\1 endright)$, где $C_1$ и $C_2$ – произвольные константы.

Продолжение этой темы рассмотрим во второй части, где разберём ещё один пример с нахождением общего решения и ФСР.

Видео:ФСР. Система однородных уравнений. Общее решениеСкачать

Система однородных линейных алгебраических уравнений всегда имеет решения отличные от нулевого если

СИСТЕМА ОДНОРОДНЫХ ЛИНЕЙНЫХ УРАВНЕНИЙ

Системой однородных линейных уравнений называется система вида

Ясно, что в этой случае , т.к. все элементы одного из столбцов в этих определителях равны нулю.

Так как неизвестные находятся по формулам , то в случае, когда Δ ≠ 0, система имеет единственное нулевое решение x = y = z = 0. Однако, во многих задачах интересен вопрос о том, имеет ли однородная система решения отличные от нулевого.

Теорема. Для того, чтобы система линейных однородных уравнений имела ненулевое решение, необходимо и достаточно, чтобы Δ ≠ 0.

Итак, если определитель Δ ≠ 0, то система имеет единственное решение. Если же Δ ≠ 0, то система линейных однородных уравнений имеет бесконечное множество решений.

Система однородных линейных алгебраических уравнений всегда имеет решения отличные от нулевого если

, а значит x=y=z=0.

СОБСТВЕННЫЕ ВЕКТОРЫ И СОБСТВЕННЫЕ ЗНАЧЕНИЯ МАТРИЦЫ

Пусть задана квадратная матрица , X – некоторая матрица–столбец, высота которой совпадает с порядком матрицы A. .

Во многих задачах приходится рассматривать уравнение относительно X

где λ – некоторое число. Понятно, что при любом λ это уравнение имеет нулевое решение .

Число λ, при котором это уравнение имеет ненулевые решения, называется собственным значением матрицы A, а X при таком λ называется собственным вектором матрицы A.

Найдём собственный вектор матрицы A. Поскольку E∙X = X, то матричное уравнение можно переписать в виде или . В развёрнутом виде это уравнение можно переписать в виде системы линейных уравнений. Действительно .

И, следовательно,

Итак, получили систему однородных линейных уравнений для определения координат x₁, x₂, x₃ вектора X. Чтобы система имела ненулевые решения необходимо и достаточно, чтобы определитель системы был равен нулю, т.е.

Это уравнение 3-ей степени относительно λ. Оно называется характеристическим уравнением матрицы A и служит для определения собственных значений λ.

Каждому собственному значению λ соответствует собственный вектор X, координаты которого определяются из системы при соответствующем значении λ.

Составим характеристическое уравнение и найдём собственные значения

₁

Если x₁ = t, то, где t Î R.
Если λ₂ = 5

ВЕКТОРНАЯ АЛГЕБРА. ПОНЯТИЕ ВЕКТРОРА

При изучении различных разделов физики встречаются величины, которые полностью определяются заданием их численных значений, например, длина, площадь, масса, температура и т.д. Такие величины называются скалярными. Однако, кроме них встречаются и величины, для определения которых, кроме численного значения, необходимо знать также их направление в пространстве, например, сила, действующая на тело, скорость и ускорение тела при его движении в пространстве, напряжённость магнитного поля в данной точке пространства и т.д. Такие величины называются векторными.

Введём строгое определение.

Направленным отрезком назовём отрезок, относительно концов которого известно, какой из них первый, а какой второй.

Вектором называется направленный отрезок, имеющий определённую длину, т.е. это отрезок определённой длины, у которого одна из ограничивающих его точек принимается за начало, а вторая – за конец. Если A – начало вектора, B – его конец, то вектор обозначается символом, кроме того, вектор часто обозначается одной буквой . На рисунке вектор обозначается отрезком, а его направление стрелкой.

Модулем или длиной вектора называют длину определяющего его направленного отрезка. Обозначается || или ||.

К векторам будем относить и так называемый нулевой вектор, у которого начало и конец совпадают. Он обозначается . Нулевой вектор не имеет определенного направления и модуль его равен нулю ||=0.

Векторы и называются коллинеарными, если они расположены на одной прямой или на параллельных прямых. При этом если векторы и одинаково направлены, будем писать , противоположно .

Векторы, расположенные на прямых, параллельных одной и той же плоскости, называются компланарными.

Два вектора и называются равными, если они коллинеарны, одинаково направлены и равны по длине. В этом случае пишут .

Из определения равенства векторов следует, что вектор можно переносить параллельно самому себе, помещая его начало в любую точку пространства.

Если дан вектор , то, выбрав любую точку , можем построить вектор , равный данному, и притом только один, или, как говорят, перенести вектор в точку .
Если рассмотреть квадрат ABCD, то на основанииопределения равенства векторов, мы можем написать и , но , , хотя все они имеют одинаковую длину.

ЛИНЕЙНЫЕ ОПЕРАЦИИ НАД ВЕКТОРАМИ

Умножение вектора на число.

Произведением вектора на число λ называется новый вектор такой, что:

;
вектор коллинеарен вектору ;
векторы и направлены одинаково, если λ>0 и противоположно, если λ

Видео:§41 Решение систем линейных однородных уравненийСкачать

Однородная система линейных уравнений

Рассмотрим систему линейных уравнений (СЛУ):

Представим (1) в матричном виде:

где A m×n матрица, x вектор столбец порядка n , 0 — нулевой вектор столбец порядка m.

СЛУ (1) (или (2)) называется однородной системой линейных уравнений, т.к. правая часть системы равна нулю.

Однородная система линейных уравнений всегда совместна, т.к. вектор 0 всегда является решением системы (1):

Это решение называется нулевым или тривиальным решением.

Cистема линейных однородных уравнений имеет ли другие решения, кроме нулевого.
При каких условиях система линейных однородных уравнений имеет нетривиальное решение.
Как найти множество всех решений системы однородных линейных уравнений.

Если A n×n матрица и rank( A)= n, то нулевой вектор является единственным решением системы (1), в противном случае система имеет множество решений.

Видео:Математика без Ху!ни. Метод Гаусса.Скачать

Обшее решение однородной системы линейных уравнений

Пусть A m×n — матрица rank A=r. В общем случае можем предположить что r r столбцов матрицы A линейно независимы. Для удобства записи предположим, что это первые r столбцы матрицы A. Переставляя строки матрицы можно добиться того, чтобы подматрица матрицы A порядка r×r, расположенная в левом верхнем углу, была невырожденной. Запишем систему (2) в блочном виде:

где M — r×r — матрица, rang M=r.

Применяя метод исключения Гаусса для системы (3), получим:

где M₁ верхняя треугольная матрица, 0 — нулевые матрицы соответствующих порядков. Далее, применяя обратный ход исключения Гаусса, и, далее, разделив элементы каждой строки на ведущий элемент этой строки (если ведущий элемент существует) получим:

где E — единичная матрица порядка r×r.

где F₂— r×(n-r) — матрица, E n-r — единичная матрица порядка n-r, X — матрица порядка n×(n-r).

В уравнении (5) вместо x подставляя матрицу (6), получим:

Таким образом, векторы столбцы матрицы X являются решением системы (2) (или (1)). Более того, эти векторы линейно независимы и их линейная комбинация также является решением (2).

Общее решение системы однородных линейных уравнений имеет следующий вид:

гдe k — произвольный вектор столбец порядка n-r.

Общее решение системы однородных линейных уравнений можно также записать в следующем виде:

где x_i — i-ый вектор-столбец матрицы X, а k_i — i-ая координата вектора k

Множество всех решений (8)(или (9)) образует ядро или нуль пространство матрицы A и обозначается через Ker (A) или N(A).

В начале этого параграфа мы предполагали, что линейные независимые r векторы столбцы расположены в начале матрицы A. В общем случае, если они расположены в произвольных местах, аналогично вышеизложенному, применяя метод Гаусса, затем обратный ход Гауссова исключения и, наконец , разделив элементы каждой строки на ведущий элемент этой строки (если ведущий элемент существует), получим

Сделаем замену переменных:

где P -матрица перестановок поядка n×n выбрана так, чтобы при подстановке (11) в (10) получили:

где E — единичная матрица порядка r×r.

Аналогично вышеизложенному векторы столбцы матрицы X’:

образуют множесво всех решений однородной системы линейных уравнений (12).

Учитывая (11) получим:

Общее решение системы однородных линейных уравнений имеет следующий вид:

гдe k — произвольный вектор столбец порядка n-r.

Общее решение системы однородных линейных уравнений можно также записать в следующем виде:

где q_i — i-ый вектор-столбец матрицы Q, а k_i — i-ая координата вектора k

Видео:Математика без Ху!ни. Метод Гаусса. Совместность системы. Ранг матрицы.Скачать

Нахождение общего решения однородной системы линейных уравнений с помощью псевдообратной матрицы

Если rank(A)= r, r общее решение можно представить в следующем виде:

где E —единичная матрица, A + — псевдообратная к A матрица.

Для проверки подставим (16) в (2):

Ax=A(E−A + A)z=(A−AA + A)z=(A−A)z=0.

Ранг матрицы rank( E−A + A)= n-r. Следовательно столбцы матрицы E−A + A образуют множество всех решений системы (2).

Отметим, что r столбцов матрицы E−A + A линейно зависимы. Для исключения линейно зависимых столбцов можно сделать скелетное разложение. Тогда E−A + A= QS, где Q n×n−r — матрица rank (Q)=n−r, S n−r×n-матрица rank (S)=n−r. Тогда множество всех решений однородной системы линейных уравнений примет следующий вид:

Видео:Метод Крамера за 3 минуты. Решение системы линейных уравнений - bezbotvyСкачать

Решение однородной системы линейных уравнений онлайн

Для решения однородной системы линейных уравнений пользуйтесь онлайн калькулятором который решает однородную систему по шагам и находит полное решение.