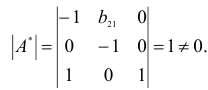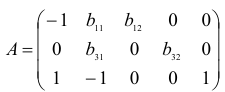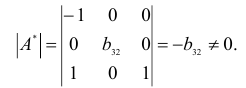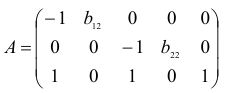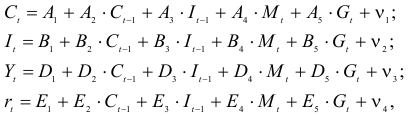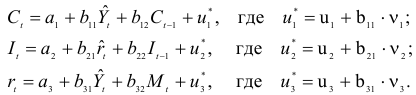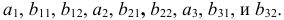Предположим, что в ходе регрессионного анализа была установлена линейная взаимосвязь между исследуемыми переменными х и у, которая описывается моделью регрессии вида:
В результате оценивания данной эконометрической модели определяются оценки неизвестных коэффициентов. Классический подход к оцениванию параметров линейной регрессии основан на методе наименьших квадратов (МНК).
Метод наименьших квадратов позволяет получить такие оценки параметров β0и β1, при которых сумма квадратов отклонений фактических значений результативного признака y от расчетных (теоретических) y˜ минимальна:
В процессе минимизации функции (1) неизвестными являются только значения коэффициентов β0 и β1, потому что значения результативной и факторной переменных известны из наблюдений. Для определения минимума функции двух переменных вычисляются частные производные этой функции по каждому из оцениваемых параметров и приравниваются к нулю. Результатом данной процедуры будет стационарная система уравнений для функции (2):
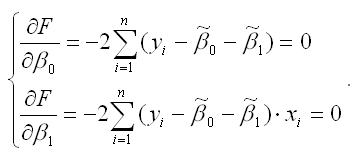
Если разделить обе части каждого уравнения системы на (-2), раскрыть скобки и привести подобные члены, то получим систему нормальных уравнений для функции регрессии вида yi=β0+β1xi:
Если решить данную систему нормальных уравнений, то мы получим искомые оценки неизвестных коэффициентов модели регрессии β0 и β1:
y – среднее значение зависимой переменной;
x – среднее значение независимой переменной;
xy – среднее арифметическое значение произведения зависимой и независимой переменных;
G 2 (x) – дисперсия независимой переменной;
Gcov (x, y) – ковариация между зависимой и независимой переменными.
Таким образом, явный вид решения системы нормальных уравнений может быть записан следующим образом:
- Метод наименьших квадратов
- В чем именно заключается МНК (метод наименьших квадратов)
- Как вывести формулы для вычисления коэффициентов
- Как изобразить МНК на графике функций
- Доказательство метода МНК
- Системы эконометрических уравнений
- Эконометрика
- Виды систем эконометрических уравнений
- Проблема идентификации
- Решение эконометрических уравнений
- Пример задачи с уравнением №4.2.1.
- Пример задачи с уравнением №4.2.2.
- Пример задачи с уравнением №4.2.3.
- Пример задачи с уравнением №4.2.4.
- 📽️ Видео
Видео:Как работает метод наименьших квадратов? Душкин объяснитСкачать

Метод наименьших квадратов
Начнем статью сразу с примера. У нас есть некие экспериментальные данные о значениях двух переменных – x и y . Занесем их в таблицу.
| i = 1 | i = 2 | i = 3 | i = 4 | i = 5 | |
| x i | 0 | 1 | 2 | 4 | 5 |
| y i | 2 , 1 | 2 , 4 | 2 , 6 | 2 , 8 | 3 , 0 |
После выравнивания получим функцию следующего вида: g ( x ) = x + 1 3 + 1 .
Мы можем аппроксимировать эти данные с помощью линейной зависимости y = a x + b , вычислив соответствующие параметры. Для этого нам нужно будет применить так называемый метод наименьших квадратов. Также потребуется сделать чертеж, чтобы проверить, какая линия будет лучше выравнивать экспериментальные данные.
Видео:Метод наименьших квадратов. Линейная аппроксимацияСкачать

В чем именно заключается МНК (метод наименьших квадратов)
Главное, что нам нужно сделать, – это найти такие коэффициенты линейной зависимости, при которых значение функции двух переменных F ( a , b ) = ∑ i = 1 n ( y i — ( a x i + b ) ) 2 будет наименьшим. Иначе говоря, при определенных значениях a и b сумма квадратов отклонений представленных данных от получившейся прямой будет иметь минимальное значение. В этом и состоит смысл метода наименьших квадратов. Все, что нам надо сделать для решения примера – это найти экстремум функции двух переменных.
Видео:11 4 Применение МНК к решению систем линейных уравненийСкачать

Как вывести формулы для вычисления коэффициентов
Для того чтобы вывести формулы для вычисления коэффициентов, нужно составить и решить систему уравнений с двумя переменными. Для этого мы вычисляем частные производные выражения F ( a , b ) = ∑ i = 1 n ( y i — ( a x i + b ) ) 2 по a и b и приравниваем их к 0 .
δ F ( a , b ) δ a = 0 δ F ( a , b ) δ b = 0 ⇔ — 2 ∑ i = 1 n ( y i — ( a x i + b ) ) x i = 0 — 2 ∑ i = 1 n ( y i — ( a x i + b ) ) = 0 ⇔ a ∑ i = 1 n x i 2 + b ∑ i = 1 n x i = ∑ i = 1 n x i y i a ∑ i = 1 n x i + ∑ i = 1 n b = ∑ i = 1 n y i ⇔ a ∑ i = 1 n x i 2 + b ∑ i = 1 n x i = ∑ i = 1 n x i y i a ∑ i = 1 n x i + n b = ∑ i = 1 n y i
Для решения системы уравнений можно использовать любые методы, например, подстановку или метод Крамера. В результате у нас должны получиться формулы, с помощью которых вычисляются коэффициенты по методу наименьших квадратов.
n ∑ i = 1 n x i y i — ∑ i = 1 n x i ∑ i = 1 n y i n ∑ i = 1 n — ∑ i = 1 n x i 2 b = ∑ i = 1 n y i — a ∑ i = 1 n x i n
Мы вычислили значения переменных, при который функция
F ( a , b ) = ∑ i = 1 n ( y i — ( a x i + b ) ) 2 примет минимальное значение. В третьем пункте мы докажем, почему оно является именно таким.
Это и есть применение метода наименьших квадратов на практике. Его формула, которая применяется для поиска параметра a , включает в себя ∑ i = 1 n x i , ∑ i = 1 n y i , ∑ i = 1 n x i y i , ∑ i = 1 n x i 2 , а также параметр
n – им обозначено количество экспериментальных данных. Советуем вам вычислять каждую сумму отдельно. Значение коэффициента b вычисляется сразу после a .
Обратимся вновь к исходному примеру.
Здесь у нас n равен пяти. Чтобы было удобнее вычислять нужные суммы, входящие в формулы коэффициентов, заполним таблицу.
| i = 1 | i = 2 | i = 3 | i = 4 | i = 5 | ∑ i = 1 5 | |
| x i | 0 | 1 | 2 | 4 | 5 | 12 |
| y i | 2 , 1 | 2 , 4 | 2 , 6 | 2 , 8 | 3 | 12 , 9 |
| x i y i | 0 | 2 , 4 | 5 , 2 | 11 , 2 | 15 | 33 , 8 |
| x i 2 | 0 | 1 | 4 | 16 | 25 | 46 |
Решение
Четвертая строка включает в себя данные, полученные при умножении значений из второй строки на значения третьей для каждого отдельного i . Пятая строка содержит данные из второй, возведенные в квадрат. В последнем столбце приводятся суммы значений отдельных строчек.
Воспользуемся методом наименьших квадратов, чтобы вычислить нужные нам коэффициенты a и b . Для этого подставим нужные значения из последнего столбца и подсчитаем суммы:
n ∑ i = 1 n x i y i — ∑ i = 1 n x i ∑ i = 1 n y i n ∑ i = 1 n — ∑ i = 1 n x i 2 b = ∑ i = 1 n y i — a ∑ i = 1 n x i n ⇒ a = 5 · 33 , 8 — 12 · 12 , 9 5 · 46 — 12 2 b = 12 , 9 — a · 12 5 ⇒ a ≈ 0 , 165 b ≈ 2 , 184
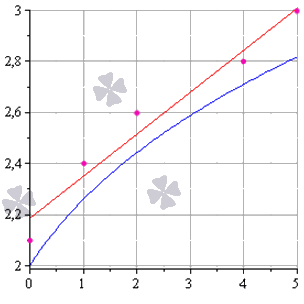
У нас получилось, что нужная аппроксимирующая прямая будет выглядеть как y = 0 , 165 x + 2 , 184 . Теперь нам надо определить, какая линия будет лучше аппроксимировать данные – g ( x ) = x + 1 3 + 1 или 0 , 165 x + 2 , 184 . Произведем оценку с помощью метода наименьших квадратов.
Чтобы вычислить погрешность, нам надо найти суммы квадратов отклонений данных от прямых σ 1 = ∑ i = 1 n ( y i — ( a x i + b i ) ) 2 и σ 2 = ∑ i = 1 n ( y i — g ( x i ) ) 2 , минимальное значение будет соответствовать более подходящей линии.
σ 1 = ∑ i = 1 n ( y i — ( a x i + b i ) ) 2 = = ∑ i = 1 5 ( y i — ( 0 , 165 x i + 2 , 184 ) ) 2 ≈ 0 , 019 σ 2 = ∑ i = 1 n ( y i — g ( x i ) ) 2 = = ∑ i = 1 5 ( y i — ( x i + 1 3 + 1 ) ) 2 ≈ 0 , 096
Ответ: поскольку σ 1 σ 2 , то прямой, наилучшим образом аппроксимирующей исходные данные, будет
y = 0 , 165 x + 2 , 184 .
Видео:Метод Наименьших Квадратов (МНК)Скачать

Как изобразить МНК на графике функций
Метод наименьших квадратов наглядно показан на графической иллюстрации. С помощью красной линии отмечена прямая g ( x ) = x + 1 3 + 1 , синей – y = 0 , 165 x + 2 , 184 . Исходные данные обозначены розовыми точками.
Поясним, для чего именно нужны приближения подобного вида.
Они могут быть использованы в задачах, требующих сглаживания данных, а также в тех, где данные надо интерполировать или экстраполировать. Например, в задаче, разобранной выше, можно было бы найти значение наблюдаемой величины y при x = 3 или при x = 6 . Таким примерам мы посвятили отдельную статью.
Видео:Метод наименьших квадратов (МНК)Скачать
Доказательство метода МНК
Чтобы функция приняла минимальное значение при вычисленных a и b , нужно, чтобы в данной точке матрица квадратичной формы дифференциала функции вида F ( a , b ) = ∑ i = 1 n ( y i — ( a x i + b ) ) 2 была положительно определенной. Покажем, как это должно выглядеть.
У нас есть дифференциал второго порядка следующего вида:
d 2 F ( a ; b ) = δ 2 F ( a ; b ) δ a 2 d 2 a + 2 δ 2 F ( a ; b ) δ a δ b d a d b + δ 2 F ( a ; b ) δ b 2 d 2 b
Решение
δ 2 F ( a ; b ) δ a 2 = δ δ F ( a ; b ) δ a δ a = = δ — 2 ∑ i = 1 n ( y i — ( a x i + b ) ) x i δ a = 2 ∑ i = 1 n ( x i ) 2 δ 2 F ( a ; b ) δ a δ b = δ δ F ( a ; b ) δ a δ b = = δ — 2 ∑ i = 1 n ( y i — ( a x i + b ) ) x i δ b = 2 ∑ i = 1 n x i δ 2 F ( a ; b ) δ b 2 = δ δ F ( a ; b ) δ b δ b = δ — 2 ∑ i = 1 n ( y i — ( a x i + b ) ) δ b = 2 ∑ i = 1 n ( 1 ) = 2 n
Иначе говоря, можно записать так: d 2 F ( a ; b ) = 2 ∑ i = 1 n ( x i ) 2 d 2 a + 2 · 2 ∑ x i i = 1 n d a d b + ( 2 n ) d 2 b .
Мы получили матрицу квадратичной формы вида M = 2 ∑ i = 1 n ( x i ) 2 2 ∑ i = 1 n x i 2 ∑ i = 1 n x i 2 n .
В этом случае значения отдельных элементов не будут меняться в зависимости от a и b . Является ли эта матрица положительно определенной? Чтобы ответить на этот вопрос, проверим, являются ли ее угловые миноры положительными.
Вычисляем угловой минор первого порядка: 2 ∑ i = 1 n ( x i ) 2 > 0 . Поскольку точки x i не совпадают, то неравенство является строгим. Будем иметь это в виду при дальнейших расчетах.
Вычисляем угловой минор второго порядка:
d e t ( M ) = 2 ∑ i = 1 n ( x i ) 2 2 ∑ i = 1 n x i 2 ∑ i = 1 n x i 2 n = 4 n ∑ i = 1 n ( x i ) 2 — ∑ i = 1 n x i 2
После этого переходим к доказательству неравенства n ∑ i = 1 n ( x i ) 2 — ∑ i = 1 n x i 2 > 0 с помощью математической индукции.
- Проверим, будет ли данное неравенство справедливым при произвольном n . Возьмем 2 и подсчитаем:
2 ∑ i = 1 2 ( x i ) 2 — ∑ i = 1 2 x i 2 = 2 x 1 2 + x 2 2 — x 1 + x 2 2 = = x 1 2 — 2 x 1 x 2 + x 2 2 = x 1 + x 2 2 > 0
У нас получилось верное равенство (если значения x 1 и x 2 не будут совпадать).
- Сделаем предположение, что данное неравенство будет верным для n , т.е. n ∑ i = 1 n ( x i ) 2 — ∑ i = 1 n x i 2 > 0 – справедливо.
- Теперь докажем справедливость при n + 1 , т.е. что ( n + 1 ) ∑ i = 1 n + 1 ( x i ) 2 — ∑ i = 1 n + 1 x i 2 > 0 , если верно n ∑ i = 1 n ( x i ) 2 — ∑ i = 1 n x i 2 > 0 .
( n + 1 ) ∑ i = 1 n + 1 ( x i ) 2 — ∑ i = 1 n + 1 x i 2 = = ( n + 1 ) ∑ i = 1 n ( x i ) 2 + x n + 1 2 — ∑ i = 1 n x i + x n + 1 2 = = n ∑ i = 1 n ( x i ) 2 + n · x n + 1 2 + ∑ i = 1 n ( x i ) 2 + x n + 1 2 — — ∑ i = 1 n x i 2 + 2 x n + 1 ∑ i = 1 n x i + x n + 1 2 = = ∑ i = 1 n ( x i ) 2 — ∑ i = 1 n x i 2 + n · x n + 1 2 — x n + 1 ∑ i = 1 n x i + ∑ i = 1 n ( x i ) 2 = = ∑ i = 1 n ( x i ) 2 — ∑ i = 1 n x i 2 + x n + 1 2 — 2 x n + 1 x 1 + x 1 2 + + x n + 1 2 — 2 x n + 1 x 2 + x 2 2 + . . . + x n + 1 2 — 2 x n + 1 x 1 + x n 2 = = n ∑ i = 1 n ( x i ) 2 — ∑ i = 1 n x i 2 + + ( x n + 1 — x 1 ) 2 + ( x n + 1 — x 2 ) 2 + . . . + ( x n — 1 — x n ) 2 > 0
Выражение, заключенное в фигурные скобки, будет больше 0 (исходя из того, что мы предполагали в пункте 2 ), и остальные слагаемые будут больше 0 , поскольку все они являются квадратами чисел. Мы доказали неравенство.
Ответ: найденные a и b будут соответствовать наименьшему значению функции F ( a , b ) = ∑ i = 1 n ( y i — ( a x i + b ) ) 2 , значит, они являются искомыми параметрами метода наименьших квадратов (МНК).
Видео:Метод наименьших квадратов, урок 1/2. Линейная функцияСкачать
Системы эконометрических уравнений
Эконометрика как учебная дисциплина на современном этапе благодаря своей универсальности и возможности практического использования для анализа реальных экономических объектов является одним из базовых курсов в системе высшего экономического образования.
| Если что-то непонятно — вы всегда можете написать мне в WhatsApp и я вам помогу! |
Видео:Метод наименьших квадратовСкачать

Эконометрика
Эконометрика — это статистико-математический анализ экономических отношений.
Сущность эконометрики заключается в модельном описании функционирования конкретной экономической системы (экономики данной страны, спроса-предложения в данное время в данном месте и т.д.). Одним из основных этапов эконометрических исследований является анализ устойчивости построенной модели, отражающей взаимосвязи между экономическими показателями, и проверка ее на адекватность реальным экономическим данным и процессам.
Виды систем эконометрических уравнений
Сложные экономические процессы описывают с помощью системы взаимосвязанных (одновременных) уравнений.
Различают несколько видов систем уравнений, применяемых в эконометрике:
• система независимых уравнений — когда каждая зависимая переменная 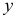
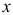
Для построения такой системы и нахождения ее параметров используется метод наименьших квадратов, применяемый к каждому уравнению в отдельности;
• система рекурсивных уравнений — когда зависимая переменная 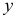
Для построения такой системы и нахождения ее параметров используется метод наименьших квадратов, применяемый последовательно к каждому уравнению в отдельности;
• система взаимосвязанных (совместных) уравнений — когда одни и те же зависимые переменные в одних уравнениях входят в левую часть, а другие в правую:
Такая система уравнений называется структурной формой модели. Для построения таких систем и нахождения их параметров используются косвенный и двухшаговый методы наименьших квадратов.
Возможно эта страница вам будет полезна:
Введем следующие определения:
- Эндогенные переменные — взаимозависимые переменные, которые определяются внутри системы (модели)
.
- Экзогенные переменные — независимые переменные, которые определяются вне системы
.
- Лаговые эндогенные переменные — эндогенные переменные за предыдущие моменты времени.
- Предопределенные переменные — экзогенные и лаговые эндогенные переменные системы.
- Коэффициенты
и
при переменных — структурные коэффициенты модели.
Система линейных функций эндогенных переменных от всех предопределенных переменных системы — приведенная форма модели:
где 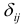
Проблема идентификации
При переходе от приведенной формы модели к структурной исследователь сталкивается с проблемой идентификации. Идентификация -это единственность соответствия между приведенной и структурной формами модели.
С позиции идентифицируемости структурные модели можно подразделить на три вида:
- идентифицируемые;
- неидентифицируемые;
- сверхидентифицируемые.
Модель идентифицируема, если все структурные ее коэффициенты определяются однозначно, единственным образом по коэффициентам приведенной формы модели, т. е. если число параметров структурной модели равно числу параметров приведенной формы модели. В этом случае структурные коэффициенты модели оцениваются через параметры приведенной формы модели и модель идентифицируема.
Модель неидентифицируема, если число приведенных коэффициентов меньше числа структурных коэффициентов, и в результате структурные коэффициенты не могут быть оценены через коэффициенты приведенной формы модели.
Модель еверхидентифицируема, если число приведенных коэффициентов больше числа структурных коэффициентов. В этом случае на основе коэффициентов приведенной формы можно получить два или более значений одного структурного коэффициента. В этой модели число структурных коэффициентов меньше числа коэффициентов приведенной формы.
Сверхидентифицируемая модель, в отличие от неидентифицируемой, модели практически решаема, но требует для этого специальных методов исчисления параметров.
Структурная модель всегда представляет собой систему совместных уравнений, каждое из которых требуется проверять на идентификацию. Модель считается идентифицируемой, если каждое уравнение системы идентифицируемо. Если хотя бы одно из уравнений системы неидентифицируемо, то и вся модель считается неидентифицируемой.
Сверхидентифицируемая модель содержит хотя бы одно сверхидентифицируемое уравнение.
Выполнение условия идентифицируемости модели проверяется для каждого уравнения системы. Чтобы уравнение было идентифицируемо, необходимо, чтобы число предопределенных переменных, отсутствующих в данном уравнении, но присутствующих в системе, было равно числу эндогенных переменных в данном уравнении без одного.
Обозначим через 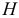
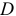
- уравнение идентифицируемо, если
;
- уравнение сверхидентифицируемо, если
;
- уравнение неидентифицируемо, если
.
Если необходимое условие выполнено, то далее проверяется достаточное условие идентификации.
Достаточное условие идентификации — определитель матрицы, составленной из коэффициентов при переменных, отсутствующих в исследуемом уравнении, не равен нулю, и ранг этой матрицы не менее числа эндогенных переменных системы без единицы.
Для решения идентифицируемого уравнения применяется косвенный метод наименьших квадратов, для решения сверхидентифицированных -двухшаговый метод наименьших квадратов.
Косвенный МНК состоит в следующем:
• составляют приведенную форму модели и определяют численные значения ее параметров обычным МНК;
• путем алгебраических преобразований переходят от приведенной формы к уравнениям структурной формы модели, получая тем самым численные оценки структурных параметров.
Двухшаговый МНК заключается в следующем:
• составляют приведенную форму модели и определяют численные значения ее параметров обычным МНК;
• выявляют эндогенные переменные, находящиеся в правой части структурного уравнения, параметры которого определяются двухшаговым МНК, и находят расчетные значения этих эндогенных переменных по соответствующим уравнениям приведенной системы;
• обычным МНК определяют параметры структурного уравнения, используя в качестве исходных данных фактические значения предопределенных переменных и расчетные значения эндогенных переменных, стоящих в правой части уравнения.
Решение эконометрических уравнений
Пример задачи с уравнением №4.2.1.
Рассматривается модель протекционизма Сальватора (упрощенная версия):
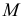
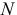
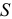
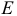
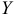
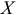
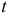
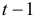
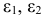
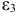
- Применив необходимое и достаточное условие идентификации определить, идентифицировано ли каждое из уравнений модели.
- Определить метод оценки параметров модели.
- Записать приведенную форму модели в общем виде.
Решение:
- Модель представляет с собой систему взаимосвязанных (одновременных) уравнений. Для ответа на вопрос о способе оценки параметров модели проверим каждое ее уравнение на идентификацию.
Модель включает три эндогенные переменные 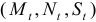
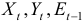
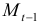
Проверим необходимое условие идентификации для уравнений модели.
Это уравнение включает три эндогенные переменные 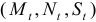
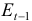
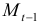
Это уравнение включает три эндогенные переменные 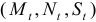
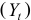
Это уравнение включает три эндогенные переменные 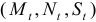
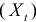
Проверим для каждого из уравнений достаточное условие идентификации. Для этого составим матрицу коэффициентов при переменных модели:
В соответствии с достаточным условием идентификации определитель матрицы коэффициентов, не входящих в исследуемое уравнение, не должен быть равен нулю, а ранг матрицы должен быть не менее, чем число эндогенных переменных модели минус 1, т.е. в данной задаче больше или равен 3-1=2.
Матрица коэффициентов при переменных, не входящих в уравнение, имеет вид
Ранг этой матрицы
Следовательно, для 1 уравнения достаточное условие выполняется, это уравнение точно идентифицируемо. 2 уравнение.
Матрица коэффициентов при переменных, не входящих в уравнение, имеет вид
Ранг этой матрицы
так как она содержит отличный от нуля минор второго порядка
Следовательно, для 2 уравнения достаточное условие выполняется, это уравнение сверхидентифицируемо. 3 уравнение.
Матрица коэффициентов при переменных, не входящих в уравнение, имеет вид
Ранг этой матрицы 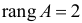
Следовательно, для 3 уравнения достаточное условие выполняется, это уравнение сверхидентифицируемо.
- Таким образом, система в целом сверхидентифицируема, для оценки ее параметров можно применить двухшаговый метод наименьших квадратов.
- Запишем приведенную форму модели в общем виде:
Пример задачи с уравнением №4.2.2.
Рассматривается структурная модель вида:
- Применив необходимое и достаточное условие идентификации определить, идентифицировано ли каждое из уравнений модели.
- Определить метод оценки параметров модели.
- Записать приведенную форму модели в общем виде.
- Исходя из приведенной формы модели уравнений
найти структурные коэффициенты модели.
Решение:
- Модель представляет с собой систему взаимосвязанных (одновременных) уравнений. Для ответа на вопрос о способе оценки параметров модели проверим каждое ее уравнение на идентификацию.
Модель включает три эндогенные переменные 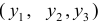
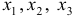
Проверим необходимое условие идентификации для уравнений модели.
Это уравнение включает две эндогенные переменные ( 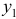
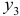
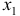
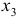
Это уравнение включает три эндогенные переменные 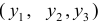
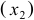
Это уравнение включает две эндогенные переменные (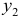
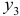
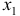
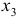
Для этого составим матрицу коэффициентов при переменных модели:
Матрица коэффициентов при переменных, не входящих в уравнение, имеет вид
что не менее чем число эндогенных переменных системы минус один. Следовательно, для первого уравнения достаточное условие идентификации выполнено, уравнение точно идентифицируемо.
Матрица коэффициентов при переменных, не входящих в уравнение, имеет вид
что не менее чем число эндогенных переменных системы минус один. Следовательно, для второго уравнения достаточное условие идентификации выполнено, уравнение точно идентифицируемо.
Матрица коэффициентов при переменных, не входящих в уравнение, имеет вид
что не менее чем число эндогенных переменных системы минус один. Следовательно, для третьего уравнения достаточное условие идентификации выполнено, уравнение точно идентифицируемо.
- Все уравнения системы точно идентифицируемы, следовательно, система в целом точно идентифицируема, для оценки ее параметров может быть применен косвенный метод наименьших квадратов.
- Запишем приведенную форму модели в общем виде:
- Вычисление структурных коэффициентов модели:
1) из третьего уравнения приведенной формы выразим 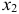
Данное выражение содержит переменные 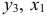
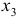
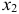
Откуда получим первое уравнение СФМ в виде
2) во втором уравнении СФМ нет переменных 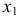

Первый этап: выразим 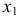
Подстановка данного выражения во второе уравнение ПФМ не решило бы задачу до конца, так как в выражении присутствует 

Подставим его в выражение для
Второй этап: аналогично, чтобы выразить 
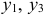
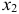

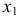
Подставим полученные 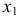

В результате получаем второе уравнение СФМ
3) из второго уравнения ПФМ выразим 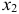
Подставим полученное выражение в третье уравнение ПФМ
В результате получаем третье уравнение СФМ
Таким образом, СФМ примет вид
Пример задачи с уравнением №4.2.3.
Изучается модель вида
где 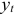
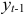
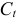
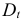
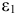
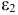
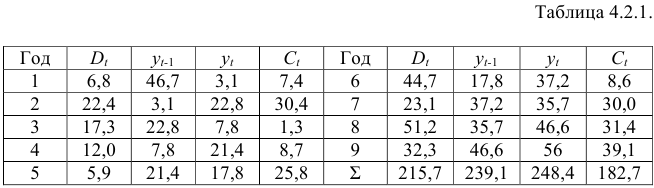
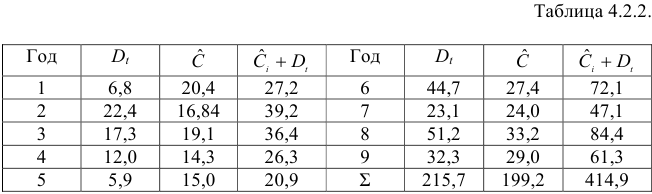
Информация за девять лет о приросте всех показателей дана в таблице 4.2.1.
Для данной модели была получена система приведенных уравнений
- Применив необходимое и достаточное условие идентификации, определить, идентифицировано ли каждое из уравнений модели.
- Рассчитать параметры первого уравнения структурной модели.
Решение:
- В данной модели две эндогенные переменные (
и
) и две экзогенные переменные (
и
). Второе уравнение точно идентифицировано, так как содержит две эндогенные переменные и не содержит одну экзогенную переменную из системы. Иными словами, для второго уравнения имеем по счетному правилу идентификации равенство: 2=1 + 1.
Первое уравнение сверхидентифицировано, так как в нем на параметры при 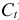
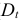
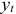
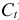
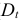
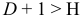
- Для определения параметров сверхидентифицированной модели используется двухшаговый метод наименьших квадратов.
Шаг 1. На основе системы приведенных уравнений по точно идентифицированному второму уравнению определим теоретические значения эндогенной переменной 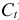
подставим значения 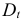
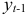
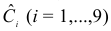
Шаг 2. По сверхидентифицированному уравнению структурной формы модели заменяем фактические значения 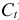
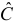
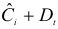
Далее к сверхидентифицированному уравнению применяется метод наименьших квадратов. Обозначим новую переменную 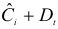
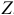
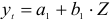
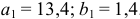
Пример задачи с уравнением №4.2.4.
Рассматривается следующая модель:
— расходы на потребление в период
;
— совокупный доход период
:
— инвестиции в период
;
— процентная ставка в период
;
— денежная масса в период
;
— государственные расходы в период
;
— расходы на потребление в период
;
— инвестиции в период
;
— текущий период;
— предыдущий период;
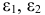
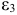
В предположении, что имеются временные ряды данных по всем переменным модели, предложить способ оценки ее параметров.
Как изменится ваш ответ на вопрос п. 1, если из модели исключить тождество дохода?
Решение:
- Модель представляет собой систему одновременных уравнений. Для ответа на вопрос о способе оценки параметров модели проверим каждое ее уравнение на идентификацию.
Модель включает четыре эндогенные переменные 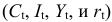
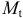
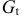
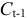
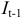
Проверим необходимое условие идентификации для уравнений модели.
Это уравнение включает две эндогенные переменные ( 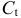
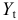
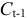
Это уравнение включает две эндогенные переменные 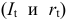
3-е уравнение тоже включает две эндогенные переменные 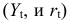
Это уравнение представляет собой тождество, параметры которого известны. Необходимости в его идентификации нет.
Проверим для каждого из уравнений достаточное условие идентификации. Для этого составим матрицу коэффициентов при переменных модели
В соответствии с достаточным условием идентификации определитель матрицы коэффициентов при переменных, не входящих в исследуемое уравнение, не должен быть равен нулю, а ранг матрицы должен быть не менее числа эндогенных переменных модели минус 1, т. е. 4-1=3.
Матрица коэффициентов при переменных, не входящих в уравнение, имеет вид
Ее ранг равен 3, так как определитель квадратной подматрицы 3×3 этой матрицы не равен нулю
Достаточное условие идентификации для 1-го уравнения выполняется.
Выпишем матрицу коэффициентов при переменных, не входящих в уравнение
Ее ранг равен 3, так как определитель квадратной подматрицы 3×3 этой матрицы не равен нулю
Достаточное условие идентификации для 2-го уравнения выполняется.
Выпишем матрицу коэффициентов при переменных, не входящих в уравнение
Ее ранг равен трем, так как имеется квадратная подматрица 3×3 этой матрицы, определитель которой не равен нулю.
Достаточное условие идентификации для 3-го уравнения выполняется.
Таким образом, все уравнения модели сверхидентифицированы. Для оценки параметров каждого из уравнений будем применять двухшаговый МНК.
Шаг 1. Запишем приведенную форму модели в общем виде
где 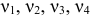
Определим параметры каждого из приведенных выше уравнений в отдельности обычным МНК. Затем найдем расчётные значения эндогенных переменных 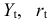
Шаг 2. В исходных структурных уравнениях заменим эндогенные переменные, выступающие в качестве факторных признаков, их расчетными значениями
Применяя к каждому из полученных уравнений в отдельности обычный МНК, определим структурные параметры
Если из модели исключить тождество дохода, число предопределенных переменных модели уменьшится на 1 (из модели будет исключена переменная 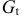
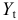
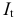
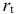
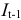
Возможно эти страницы вам будут полезны:




















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
📽️ Видео
Метод наименьших квадратов. Квадратичная аппроксимацияСкачать

ЦОС Python #1: Метод наименьших квадратовСкачать

Численные методы: Метод наименьших квадратовСкачать

Метод наименьших квадратов. ТемаСкачать

Суть метода наименьших квадратов с примерами. Основы эконометрики в RСкачать

Метод наименьших квадратов. Регрессионный анализ.Скачать

Видеоурок "Системы дифференциальных уравнений"Скачать

Построение уравнения линейной регрессии методом наименьших квадратов.Скачать

Подкаст №40. Нарциссическое, шизоидное и пограничное расстройство личности / Личностные адаптацииСкачать

11 1 Метод наименьших квадратов ВведениеСкачать

«Фин. грамотность — от классиков до современности: советы литературных гениев и цифровые решения»Скачать

Решение системы уравнений методом ГауссаСкачать

Способы решения систем нелинейных уравнений. 9 класс.Скачать

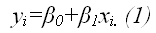
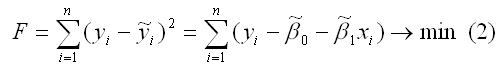
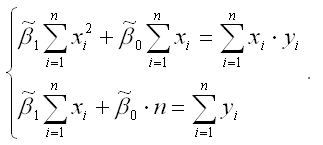
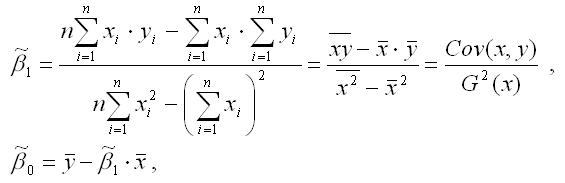

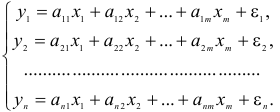
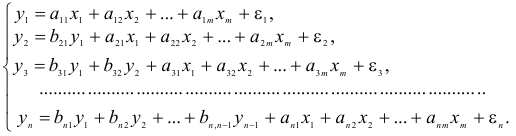
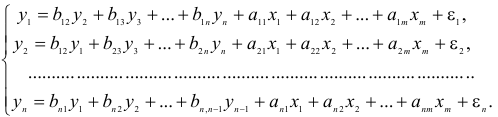
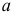 и
и 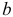 при переменных — структурные коэффициенты модели.
при переменных — структурные коэффициенты модели.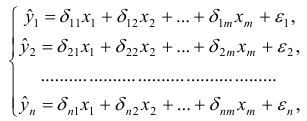
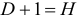 ;
;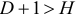 ;
;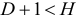 .
.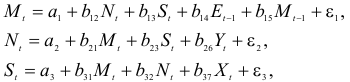

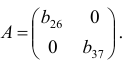
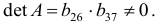
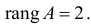
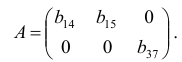
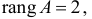
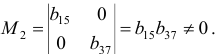
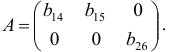
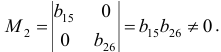
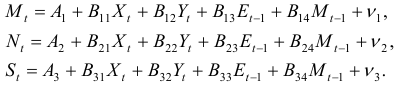
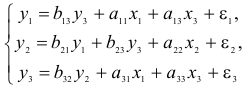
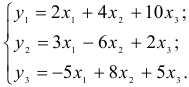

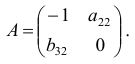
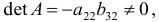
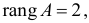
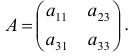
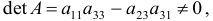
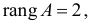
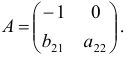
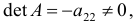
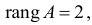
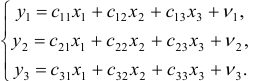
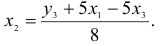
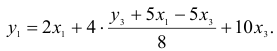
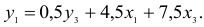
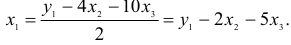
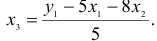
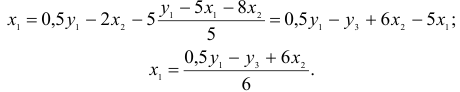
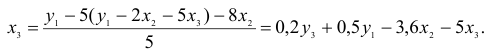
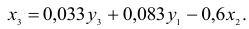
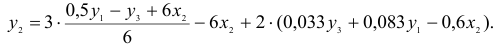
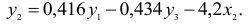
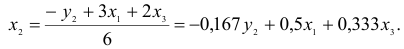
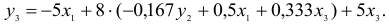
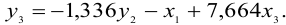
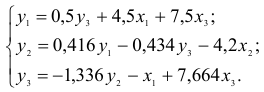
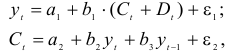
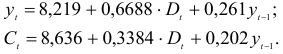
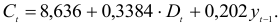
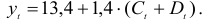
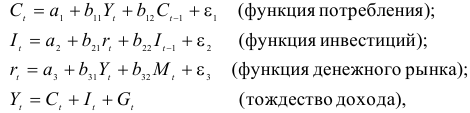
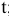 ;
;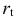 — процентная ставка в период
— процентная ставка в период 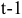 ;
;