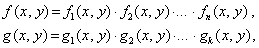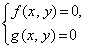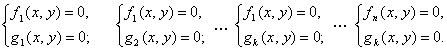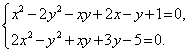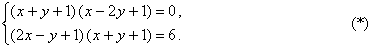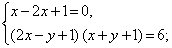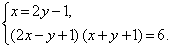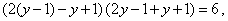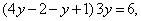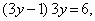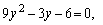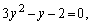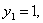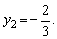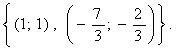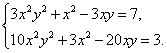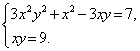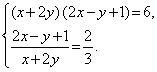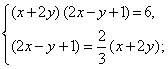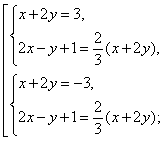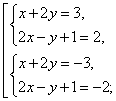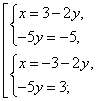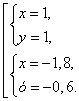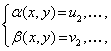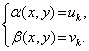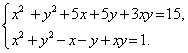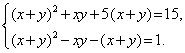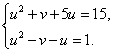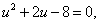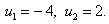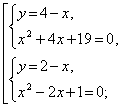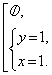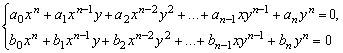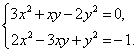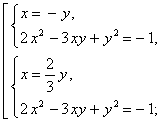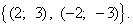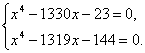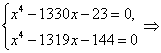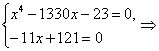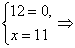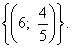- Численные методы решения систем нелинейных уравнений
- Введение
- Возможности решателя scipy.optimize.root для численного решения систем алгебраических нелинейных уравнений
- Методы решения систем нелинейных уравнений
- Выбор модельной функции
- Программа для тестирования на модельной функции c результатами решения системы алгебраических нелинейных уравнений с помощью библиотечной функции optimize.root для разных методов отыскания корней
- Программа для тестирования на модельной функции c результатами решения системы алгебраических нелинейных уравнений с помощью программы написанной на Python 3 с учётом соотношений (1)-(8) для отыскания корней по модифицированному методу Ньютона
- Система нелинейных уравнений с тремя неизвестными
- Нелинейные уравнения с двумя неизвестными
- Системы из двух уравнений, одно из которых линейное
- Однородные уравнения второй степени с двумя неизвестными
- Системы из двух уравнений, одно из которых однородное
- Системы из двух уравнений, сводящиеся к системам, в которых одно из уравнений однородное
- Примеры решения систем уравнений других видов
- Системы с нелинейными уравнениями
- Нелинейные уравнения с двумя неизвестными
- Системы из двух уравнений, одно из которых линейное
- Однородные уравнения второй степени с двумя неизвестными
- Системы из двух уравнений, одно из которых однородное
- Системы из двух уравнений, сводящиеся к системам, в которых одно из уравнений однородное
- Примеры решения систем уравнений других видов
- 📹 Видео
Видео:Система с тремя переменнымиСкачать
Численные методы решения систем нелинейных уравнений
Введение
Многие прикладные задачи приводят к необходимости нахождения общего решения системы нелинейных уравнений. Общего аналитического решения системы нелинейных уравнений не найдено. Существуют лишь численные методы.
Следует отметить интересный факт о том, что любая система уравнений над действительными числами может быть представлена одним равносильным уравнением, если взять все уравнения в форме 
, возвести их в квадрат и сложить.
Для численного решения применяются итерационные методы последовательных приближений (простой итерации) и метод Ньютона в различных модификациях. Итерационные процессы естественным образом обобщаются на случай системы нелинейных уравнений вида:
(1)
Обозначим через 
вектор неизвестных и определим вектор-функцию 
Тогда система (1) записывается в виде уравнения:
(2)
Теперь вернёмся к всеми любимому Python и отметим его первенство среди языков программирования, которые хотят изучать [1].
Этот факт является дополнительным стимулом рассмотрения числительных методов именно на Python. Однако, среди любителей Python бытует мнение, что специальные библиотечные функции, такие как scipy.optimize.root, spsolve_trianular, newton_krylov, являются самым лучшим выбором для решения задач численными методами.
С этим трудно не согласится хотя бы потому, что в том числе и разнообразие модулей подняло Python на вершину популярности. Однако, существуют случаи, когда даже при поверхностном рассмотрении использование прямых известных методов без применения специальных функций библиотеки SciPy тоже дают неплохие результаты. Иными словами, новое- это хорошо забытое старое.
Так, в публикации [2], на основании проведенных вычислительных экспериментов, доказано, что библиотечная функция newton_krylov, предназначенная для решения больших систем нелинейных уравнений, имеет в два раза меньшее быстродействие, чем алгоритм TSLS+WD
(two-step least squares), реализованный средствами библиотеки NumPy.
Целью настоящей публикации является сравнение по числу итераций, быстродействию, а главное, по результату решения модельной задачи в виде системы из ста нелинейных алгебраических уравнений при помощи библиотечной функции scipy.optimize.root и методом Ньютона, реализованного средствами библиотеки NumPy.
Возможности решателя scipy.optimize.root для численного решения систем алгебраических нелинейных уравнений
Библиотечная функция scipy.optimize.root выбрана в качестве базы сравнения, потому что имеет обширную библиотеку методов, пригодных для сравнительного анализа.
scipy.optimize.root(fun, x0, args=(), method=’hybr’, jac=None, tol=None,callback=None, ptions=None)
fun — Векторная функция для поиска корня.
x0 –Начальные условия поиска корней
method:
hybr -используется модификация Пауэлл гибридный метод;
lm – решает системы нелинейных уравнений методом наименьших квадратов.
Как следует из документации [3] методы broyden1, broyden2, anderson, linearmixing, diagbroyden, excitingmixing, krylov являются точными методами Ньютона. Остальные параметры являются «не обязательными» и с ними можно ознакомится в документации.
Методы решения систем нелинейных уравнений
Приведенный далее материал действительно можно прочитать в литературе, например в [4], но я уважаю своего читателя и для его удобства приведу вывод метода по возможности в сокращенном виде. Те, кто не любит формулы, этот раздел пропускают.
В методе Ньютона новое приближение для решения системы уравнений (2) определяется из решения системы линейных уравнений:
(3)
Определим матрицу Якоби:
(4)
Запишем(3) в виде:
(5)
Многие одношаговые методы для приближенного решения (2) по аналогии с двухслойными итерационными методами для решения систем линейных алгебраических уравнений можно записать в виде:
(6)
где 
— итерационные параметры, a 
— квадратная матрица n х n, имеющая обратную.
При использовании записи (6) метод Ньютона (5) соответствует выбору:
Система линейных уравнений (5) для нахождения нового приближения 
может решаться итерационно. В этом случае мы имеем двухступенчатый итерационный процесс с внешними и внутренними итерациями. Например, внешний итерационный процесс может осуществляться по методу Ньютона, а внутренние итерации — на основе итерационного метода Зейделя
При решении систем нелинейных уравнений можно использовать прямые аналоги стандартных итерационных методов, которые применяются для решения систем линейных уравнений. Нелинейный метод Зейделя применительно к решению (2) дает:
(7)
В этом случае каждую компоненту нового приближения из решения нелинейного уравнения, можно получить на основе метода простой итерации и метода Ньютона в различных модификациях. Тем самым снова приходим к двухступенчатому итерационному методу, в котором внешние итерации проводятся в соответствии с методом Зейделя, а внутренние — с методом Ньютона.
Основные вычислительные сложности применения метода Ньютона для приближенного решения систем нелинейных уравнений связаны с необходимостью решения линейной системы уравнений с матрицей Якоби на каждой итерации, причем от итерации к итерации эта матрица меняется. В модифицированном методе Ньютона матрица Якоби обращается только один раз:
(8)
Выбор модельной функции
Такой выбор не является простой задачей, поскольку при увеличении числа уравнений в системе в соответствии с ростом числа переменных результат решения не должен меняться, поскольку в противном случае невозможно отследить правильность решения системы уравнений при сравнении двух методов. Привожу следующее решение для модельной функции:
Функция f создаёт систему из n нелинейных уравнений, решение которой не зависит от числа уравнений и для каждой из n переменных равно единице.
Программа для тестирования на модельной функции c результатами решения системы алгебраических нелинейных уравнений с помощью библиотечной функции optimize.root для разных методов отыскания корней
Только один из методов, приведенных в документации [3] прошёл тестирование по результату решения модельной функции, это метод ‘krylov’.
Решение для n=100:
Solution:
[1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1.]
Krylov method iteration = 4219
Optimize root time 7.239 seconds:
Вывод: С увеличением числа уравнений вдвое заметно появление ошибок в решении. При дальнейшем увеличении n решение становится не приемлемым, что возможно из-за автоматической адаптации к шагу, эта же причина резкого падения быстродействия. Но это только моё предположение.
Программа для тестирования на модельной функции c результатами решения системы алгебраических нелинейных уравнений с помощью программы написанной на Python 3 с учётом соотношений (1)-(8) для отыскания корней по модифицированному методу Ньютона
Решение для n=100:
Solution:
[1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1.]
Newton iteration = 13
Newton method time 0.496 seconds
Решение для n=200:
Solution:
[1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1.]
Newton iteration = 14
Newton method time 1.869 seconds
Чтобы убедиться в том, что программа действительно решает систему, перепишем модельную функцию для ухода от корня со значением 1 в виде:
Получим:
Solution:
[ 0.96472166 0.87777036 0.48175823 -0.26190496 -0.63693762 0.49232062
-1.31649896 0.6865098 0.89609091 0.98509235]
Newton iteration = 16
Newton method time 0.046 seconds
Вывод: Программа работает и при изменении модельной функции.
Теперь вернёмся к начальной модельной функции и проверим более широкий диапазон для n, например в 2 и 500.
n=2
Solution:
[1. 1.]
Newton iteration = 6
Newton method time 0.048 seconds
n=500
Видео:После этого видео, ТЫ РЕШИШЬ ЛЮБУЮ Систему Нелинейных УравненийСкачать
Система нелинейных уравнений с тремя неизвестными
1) Метод подстановки.
Идея метода. Выбирается уравнение, в котором одна из переменных наиболее просто выражается через остальные переменные. Полученное выражение этой переменной подставляется в оставшиеся уравнения системы.
- b) Комбинирование с другими методами.
Идея метода. Если метод прямой подстановки не применим на начальном этапе решения, то используются равносильные преобразования систем (почленное сложение, вычитание, умножение, деление), а затем проводят непосредственно прямую подстановку.
2) Метод независимого решения одного из уравнений.
Идея метода. Если в системе содержится уравнение, в котором находятся взаимно обратные выражения, то вводится новая переменная и относительно её решается уравнение. Затем система распадается на несколько более простых систем.
Решить систему уравнений
Рассмотрим первое уравнение системы:
Сделав замену 
, где t ≠ 0, получаем 
Возвращаясь к старым переменным, рассмотрим два случая.
Корнями уравнения 4у 2 – 15у – 4 = 0 являются у1 = 4, у2 = — 1/4 .
Корнями уравнения 4х 2 + 15х – 4 = 0 являются х1 = — 4, х2 = 1/4 .
3)Сведение системы к объединению более простых систем.
- a) Разложение на множители способом вынесения общего множителя.
Идея метода. Если в одном из уравнений есть общий множитель, то это уравнение раскладывают на множители и, учитывая равенство выражения нулю, переходят к решению более простых систем.
- b) Разложение на множители через решение однородного уравнения.
Идея метода. Если одно из уравнений представляет собой однородное уравнение ( , то решив его относительно одной из переменных, раскладываем на множители, например: a(x-x1)(x-x2) и, учитывая равенство выражения нулю, переходим к решению более простых систем.
Решим первую систему 
Идея метода. Если в системе есть выражение, представляющее собой произведение переменных величин, то применяя метод алгебраического сложения, получают однородное уравнение, а затем используют метод разложение на множители через решение однородного уравнения.
4) Метод алгебраического сложения.
Идея метода. В одном из уравнений избавляемся от одной из неизвестных, для этого уравниваем модули коэффициентов при одной из переменных, затем производим или почленное сложение уравнений, или вычитание.
5) Метод умножения уравнений.
Идея метода. Если нет таких пар (х;у), при которых обе части одного из уравнений обращаются в ноль одновременно, то это уравнение можно заменить произведением обоих уравнений системы.
Решим второе уравнение системы.
Пусть 
= t, тогда 4t 3 + t 2 -12t -12 = 0. Применяя следствие из теоремы о корнях многочлена, имеем t1 = 2.
Р(2) = 4∙2 3 + 2 2 — 12∙2 – 12 = 32 + 4 — 24 — 12 = 0. Понизим степень многочлена, используя метод неопределенных коэффициентов.
4t 3 + t 2 -12t -12 = (t – 2) (at 2 + bt + c).
4t 3 +t 2 -12t -12 = at 3 + bt 2 + ct — 2at 2 -2bt — 2c.
4t 3 + t 2 — 12t -12 = at 3 + (b – 2a) t 2 + (c -2b) t — 2c.
Получаем уравнение 4t 2 + 9t + 6 = 0, которое не имеет корней, так как D = 9 2 — 4∙4∙6 = -15 2 + у 2 = (х + у) 2 – 2ху = а 2 – 2в; х 3 + у 3 = (х + у)(х 2 – ху + у 2 ) = а(а 2 -3в);
х 2 у + ху 2 = ху (х + у) = ав; (х +1)∙(у +1) = ху +х +у+1 =а + в +1;
10) «Граничные задачи».
Идея метода. Решение системы получаются путем логических рассуждений, связанных со структурой области определения или множества значений функций, исследование знака дискриминанта квадратного уравнения.
Особенность этой системы в том, что число переменных в ней больше числа уравнений. Для нелинейных систем такая особенность часто является признаком «граничной задачи». Исходя из вида уравнений, попытаемся найти множество значений функции , которая встречается и в первом, и во втором уравнении системы. Так как х 2 + 4 ≥ 4, то из первого уравнения следует, что
Ответ (0;4;4), (0;-4;-4).
11) Графический метод.
Идея метода. Строят графики функций в одной системе координат и находят координаты точек их пересечения.
1) Переписав первое уравнение систем в виде у = х 2 , приходим к выводу: графиком уравнения является парабола.
2) Переписав второе уравнение систем в виде у =2/х 2 , приходим к выводу: графиком уравнения является гипербола.
3) Парабола и гипербола пересекаются в точке А. Точка пересечения только одна, поскольку правая ветвь параболы служит графиком возрастающей функции, а правая ветвь гиперболы — убывающей. Судя по построенной геометрической модели точка А имеет координаты (1;2). Проверка показывает, что пара (1;2) является решением обоих уравнений системы.
На итоговой аттестации в 9-х классах по модернизированным программам, предлагаются задачи, в которых требуется решить системы алгебраических, нелинейных уравнений. Школьники испытывают большие затруднения, встречаясь с такими заданиями, особенно, если речь идет о нелинейных системах уравнений. Этот раздел алгебры по праву считается одним из трудных, так как нет единых способов решения систем алгебраических уравнений.
Необходимо помочь школьникам преодолеть трудности при решении алгебраических систем нелинейных уравнений, научить отыскивать наиболее рациональный способ решения систем уравнений, тем самым подготовить выпускника основной школы к сдаче экзамена по математике, продолжению образования в выпускных классах средней школы с профильным обучением, а затем в вузе, где дисциплины математического цикла являются профильными.
Материал статьи излагается как углубленное изучение вопросов, связанных с решением нелинейных систем уравнений в 9 классе, предусмотренных программой основного курса математики.
Предлагаются некоторые способы решения нелинейных систем уравнений. Причем, среди предлагаемых примеров имеются, как достаточно простые, так и сложные.
При решении систем уравнений применяются различные методы:
а) разложение на множители;
б) исключение переменных;
в) алгебраическое сложение;
г) замена переменных;
д) системы однородных уравнений;
ж) метод введения новых переменных;
з) графический метод.
Рассмотрим некоторые методы решения нелинейных систем уравнений.
1. Метод разложения на множители
Метод разложения на множители алгебраических систем двух уравнений с двумя неизвестными заключается в следующем. Если в алгебраической системе
то всякое решение системы уравнений
является решением совокупности систем
Пример 1. Решить систему
Решение. Так как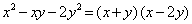 
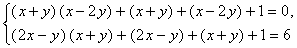
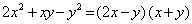
, а 
или
, то получаем:
Заметим, что множитель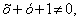 
так как в этом случае правая часть второго уравнения системы также обратилась бы в нуль. Следовательно, система (*) равносильна системе
Решим второе уравнение:
Выразив x из первого уравнения и подставив во второе, получили уравнения для нахождения y. В первое уравнение системы вместо y подставляем найденное значение и находим значения x
, 
Ответ: 
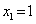
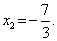
2. Метод исключения одной из неизвестных
Метод исключения неизвестных позволяет последовательно сводить решение данной системы к решению системы (или совокупности систем), содержащей на одну переменную меньше. Этот метод последовательного исключения основан на очевидном утверждении, что система уравнений
равносильна системе уравнений
и аналогично для большего числа переменных.
Пример 2. Решить систему 
Решение. Левые части уравнений системы содержат одни и те же комбинации неизвестных. Умножим уравнения на подходящие множители с тем, чтобы исключить из системы одно из неизвестных. Из системы исключим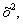 
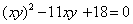
сложив второе уравнение с первым, умноженным на -3. В результате получаем уравнение 
.
Решим данное уравнение путем замены.
Пусть xy = t, тогда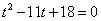 
, t1=2, t2=9.
Таким образом, исходная система распадается на системы:
и 
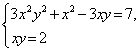
В первом случае находим x 2 =1. Если x=1 то y=2 , а если x=-1, то y=-2.
Во втором случае, исключая , получаем x 2 =-209. Поэтому вторая из двух последних систем не имеем действительных решений.
3. Метод алгебраических преобразований уравнений системы
Уравнения системы можно складывать, вычитать, умножать на число, перемножать, делить, соблюдая при этом возможность выполнения таких операций. Заметим, что следствие системы, получаемое в результате алгебраических преобразований, содержит все решения исходной системы, и, кроме того, оно может содержать лишние корни.
Поэтому: 1) если следствие не имеет решений, то и исходная система не имеет решений; 2) если решениями следствия окажутся действительными числа, то их нужно подставить в исходную систему и проверить, являются ли они ее корнями; 3) если решениями следствиями окажутся алгебраические выражения, то их нужно рассматривать совместно с уравнениями исходной системы. В этом случае получим равносильную систему или совокупность систем.
Пример 3. Решить систему 
Решение. ОДЗ: 
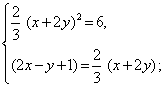
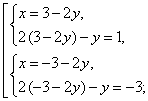
4. Метод замены переменных
Метод замены неизвестных основан на следующем утверждении.
Пусть дана система уравнений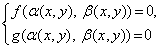 
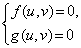
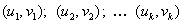
и пусть система 
имеет k различных решений 
.
Тогда система (1) равносильна совокупности k систем
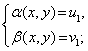
Пример 4. Решить систему 
Решение. 
Произведем замену. Пусть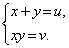 
Тогда 
Складывая уравнения, получим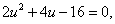 
Преобразуем первое уравнение:
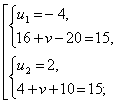
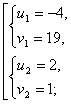
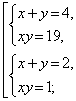
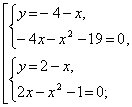
5. Системы однородных уравнений
Система двух уравнений с двумя переменными вида
называется однородной (левые части обоих уравнений однородные многочлены степени n от двух переменных).
Однородные системы решаются комбинацией двух методов: линейного преобразования и введения новых переменных.
Пример 5. Решить систему 
Решение. Первое уравнение системы однородное (напомним, что уравнение вида f(x,y)=0 где f(x,y) – однородный многочлен – называется однородным уравнением). Заметим, что если положить y=0 то из однородного уравнения 3x 2 +xy-2y 2 =0 находим x=0. Но пара чисел (0;0) не удовлетворяет второму уравнению системы, поэтому y≠0 и, следовательно, обе части однородного уравнения 3x 2 +xy-2y 2 =0 можно разделить на y 2 (это не приведёт к потере корней).
Получим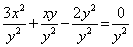 
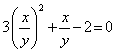
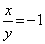
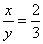
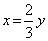
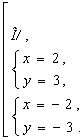
и 
, откуда находим, что 
или 
, т.е. x= – y или 
.
Ответ: 
Типичные ошибки при решении систем и методы их устранения
При решении некоторых систем иногда происходит потеря корней в ответе или появляются посторонние корни. Основная причина этого заключается в том, что осуществляются правдоподобные рассуждения, но теряется контроль над равносильностью переходов от одной системы к другой. Для того чтобы избежать подобных ошибок, нужно знать природу их появления и на определенном этапе решения произвести необходимые преобразования, проверку решения и т.д.
В качестве таких примеров рассмотрим решение нескольких систем нелинейных уравнений.
Пример 1. Решите систему уравнений 
Неправильное решение. Вычтем из первого уравнения системы второе уравнение. Получим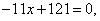 
откуда x =11.
В этом случае корень уравнения, полученный после эквивалентного преобразования (вычли второе уравнение из первого), не проверили. Чтобы избежать подобной ошибки, необходимо после вычитания одного уравнения из другого решать систему уравнений, в которой обязательным является наличие уравнения, полученное после вычитания и одного из первоначальных уравнений.
Правильное решение. Выполним эквивалентные преобразования:
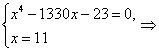
Таким образом, при решении системы уравнений, необходимо записать такое же количество уравнений, которое было в условии, чтобы не получить посторонний корень.
Правильный ответ: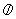 
.
Пример 2. Решить систему уравнений
(1)
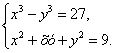
Решение. Выполним тождественное преобразование: разделим первое уравнение системы на второе уравнение, получим:
(2)
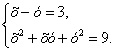
Решая систему методом подстановки, получим множество решений: .
Система (2) получена из системы (1) делением на число, отличное от нуля, поэтому системы (1) и (2) эквивалентны.
При решении систем нелинейных уравнений необходимо помнить о том, что такое тождественное преобразование как деление одного уравнения на другое не всегда приведет к правильному решению, так как может произойти потеря корня. Покажем это на следующем примере.
Пример 3. Решить систему уравнений
(3)
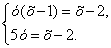
Решение. Выполним тождественное преобразование: разделим первое уравнение системы на второе уравнение, получим:
Ответ: 
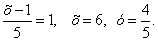
Но в этом случае произошла потеря решения . Это произошло потому, что при делении не было наложено условие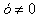 
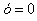
. Рассматривая условие 
, получаем х = 2.
Значит, метод деления одного уравнения на другое не безупречен, т.е. при переходе от системы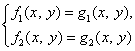 
к системе 
можем потерять решения.
- Азаров А.И., Барвенов С.А., Федосенко В.С., Шибут А.С. Системы алгебраических уравнений. Текстовые задачи. Справочное пособие для абитуриентов и школьников. 1998. – 288 с.
- Виленкин Н.Я., Ивашев-Мусатов О.С., Шварцбурд С.И. Алгебра и математический анализ для 11 класса. Учеб. пособие для учащихся шк. и классов с углубл. изуч. математики. 4-е изд. – М.: Просвещение, 1995. – 335 с.
- Галицкий М.Л., Гольдман А.М., Звавич Л.И. Сборник задач по алгебре для 8-9 классов. Учеб. пособие для учащихся шк. и классов с углубл. изуч. курса математики. М.: Просвещение, 1992. – 271 с.
- Самусенко А.В., Казаченок В.В. Математика: Типичные ошибки абитуриентов. 2-е изд., испр. – Мн.: Выш. шк., 1995.- 185 с.
- Шарыгин И.Ф., Голубев В.И. Факультативный курс по математике: Решение задач. Учеб. пособие для 11 класса средней школы. – М.: Просвещение, 1991. – 384 с.
 Нелинейные уравнения с двумя неизвестными |
| Системы из двух уравнений, одно из которых линейное |
| Однородные уравнения второй степени с двумя неизвестными |
| Системы из двух уравнений, одно из которых однородное |
| Системы из двух уравнений, сводящиеся к системам, в которых одно из уравнений однородное |
| Примеры решения систем уравнений других видов |
Видео:Способы решения систем нелинейных уравнений. 9 класс.Скачать
Нелинейные уравнения с двумя неизвестными
Определение 1 . Пусть A – некоторое множество пар чисел (x ; y) . Говорят, что на множестве A задана числовая функция z от двух переменных x и y , если указано правило, с помощью которого каждой паре чисел из множества A ставится в соответствие некоторое число.
Задание числовой функции z от двух переменных x и y часто обозначают так:
| z = f (x , y) , | (1) |
причем в записи (1) числа x и y называют аргументами функции , а число z – значением функции , соответствующим паре аргументов (x ; y) .
Определение 2 . Нелинейным уравнением с двумя неизвестными x и y называют уравнение вида
| f (x , y) = 0 , | (2) |
где f (x , y) – любая функция, отличная от функции
где a , b , c – заданные числа.
Определение 3 . Решением уравнения (2) называют пару чисел (x ; y) , для которых формула (2) является верным равенством.
Пример 1 . Решить уравнение
| x 2 – 4xy + 6y 2 – – 12 y +18 = 0 . | (3) |
Решение . Преобразуем левую часть уравнения (3):
Таким образом, уравнение (3) можно переписать в виде
| (x – 2y) 2 + 2(y – 3) 2 = 0 . | (4) |
Поскольку квадрат любого числа неотрицателен, то из формулы (4) вытекает, что неизвестные x и y удовлетворяют системе уравнений
решением которой служит пара чисел (6 ; 3) .
Пример 2 . Решить уравнение
| sin (xy) = 2 . | (5) |
вытекает, что уравнение (5) решений не имеет.
Ответ : Решений нет.
Пример 3 . Решить уравнение
| ln (x – y) = 0 . | (6) |
Следовательно, решением уравнения (6) является бесконечное множество пар чисел вида
где y – любое число.
Видео:Решение системы уравнений с тремя неизвестными с помощью формул Крамера | Высшая математикаСкачать
Системы из двух уравнений, одно из которых линейное
Определение 4 . Решением системы уравнений
называют пару чисел (x ; y) , при подстановке которых в каждое из уравнений этой системы получается верное равенство.
Системы из двух уравнений, одно из которых линейное, имеют вид
где a , b , c – заданные числа, а g(x , y) – функция двух переменных x и y .
Пример 4 . Решить систему уравнений
 | (7) |
Решение . Выразим из первого уравнения системы (7) неизвестное y через неизвестное x и подставим полученное выражение во второе уравнение системы:
Таким образом, решениями системы (7) являются две пары чисел
и 
Ответ : (– 1 ; 9) , (9 ; – 1)
Видео:Решение систем с тремя переменными. Практическая часть. 9 класс.Скачать
Однородные уравнения второй степени с двумя неизвестными
Определение 5 . Однородным уравнением второй степени с двумя неизвестными x и y называют уравнение вида
где a , b , c – заданные числа.
Пример 5 . Решить уравнение
| 3x 2 – 8xy + 5y 2 = 0 . | (8) |
Решение . Для каждого значения y рассмотрим уравнение (8) как квадратное уравнение относительно неизвестного x . Тогда дискриминант D квадратного уравнения (8) будет выражаться по формуле
откуда с помощью формулы для корней квадратного уравнения найдем корни уравнения (8):
Ответ . Решениями уравнения (8) являются все пары чисел вида
( y ; y) или 
где y – любое число.
Следствие . Левую часть уравнения (8) можно разложить на множители
Видео:Способы решения систем нелинейных уравнений. Практическая часть. 9 класс.Скачать
Системы из двух уравнений, одно из которых однородное
Системы из двух уравнений, одно из которых однородное, имеют вид
где a , b , c – заданные числа, а g(x , y) – функция двух переменных x и y .
Пример 6 . Решить систему уравнений
 | (9) |
рассматривая его как квадратное уравнение относительно неизвестного x :
.
В случае, когда x = – y , из второго уравнения системы (9) получаем уравнение
корнями которого служат числа y1 = 2 , y2 = – 2 . Находя для каждого из этих значений y соответствующее ему значение x , получаем два решения системы: (– 2 ; 2) , (2 ; – 2) .
,
из второго уравнения системы (9) получаем уравнение
которое корней не имеет.
Ответ : (– 2 ; 2) , (2 ; – 2)
Видео:СИСТЕМА УРАВНЕНИЙ нелинейных 9 класс алгебраСкачать
Системы из двух уравнений, сводящиеся к системам, в которых одно из уравнений однородное
Пример 7 . Решить систему уравнений
 | (10) |
Решение . Совершим над системой (10) следующие преобразования:
- второе уравнение системы оставим без изменений;
- к первому уравнению, умноженному на 5 , прибавим второе уравнение, умноженное на 3 , и запишем полученный результат вместо первого уравнения системы (10).
В результате система (10) преобразуется в равносильную ей систему (11), в которой первое уравнение является однородным уравнением:
 | (11) |
рассматривая его как квадратное уравнение относительно неизвестного x :
.
В случае, когда x = – 5y , из второго уравнения системы (11) получаем уравнение
которое корней не имеет.
,
из второго уравнения системы (11) получаем уравнение
,
корнями которого служат числа y1 = 3 , y2 = – 3 . Находя для каждого из этих значений y соответствующее ему значение x , получаем два решения системы: (– 2 ; 3) , (2 ; – 3) .
Ответ : (– 2 ; 3) , (2 ; – 3)
Видео:Метод Крамера за 3 минуты. Решение системы линейных уравнений - bezbotvyСкачать
Примеры решения систем уравнений других видов
Пример 8 . Решить систему уравнений (МФТИ)
Решение . Введем новые неизвестные u и v , которые выражаются через x и y по формулам:
 | (13) |
Для того, чтобы переписать систему (12) через новые неизвестные, выразим сначала неизвестные x и y через u и v . Из системы (13) следует, что
 | (14) |
Решим линейную систему (14), исключив из второго уравнения этой системы переменную x . С этой целью совершим над системой (14) следующие преобразования:
- первое уравнение системы оставим без изменений;
- из второго уравнения вычтем первое уравнение и заменим второе уравнение системы на полученную разность.
В результате система (14) преобразуется в равносильную ей систему
из которой находим
 | (15) |
Воспользовавшись формулами (13) и (15), перепишем исходную систему (12) в виде
 | (16) |
У системы (16) первое уравнение – линейное, поэтому мы можем выразить из него неизвестное u через неизвестное v и подставить это выражение во второе уравнение системы:
Следовательно, решениями системы (16) являются две пары чисел
Из формул (13) вытекает, что 
, поэтому первое решение должно быть отброшено. В случае u2 = 5, v2 = 2 из формул (15) находим значения x и y :
Определение 6 . Решением системы из двух уравнений с тремя неизвестными называют тройку чисел (x ; y ; z) , при подстановке которых в каждое уравнение системы получается верное равенство.
Пример 9 . Решить систему из двух уравнений с тремя неизвестными
 | (17) |
Решение . У системы (17) первое уравнение – линейное, поэтому мы можем выразить из него неизвестное z через неизвестные x и y и подставить это выражение во второе уравнение системы:
 | (18) |
Перепишем второе уравнение системы (18) в другом виде:
Поскольку квадрат любого числа неотрицателен, то выполнение последнего равенства возможно лишь в случае x = 4, y = 4 .
Ответ : (4 ; 4 ; – 4)
Замечание . Рекомендуем посетителю нашего сайта, интересующемуся методами решения систем уравнений, ознакомиться также c разделом справочника «Системы линейных уравнений» и нашим учебным пособием «Системы уравнений».
Видео:Решение системы трех уравнений по формулам КрамераСкачать
Системы с нелинейными уравнениями
| Нелинейные уравнения с двумя неизвестными |
| Системы из двух уравнений, одно из которых линейное |
| Однородные уравнения второй степени с двумя неизвестными |
| Системы из двух уравнений, одно из которых однородное |
| Системы из двух уравнений, сводящиеся к системам, в которых одно из уравнений однородное |
| Примеры решения систем уравнений других видов |
Видео:Решение системы линейных уравнений с двумя переменными способом подстановки. 6 класс.Скачать
Нелинейные уравнения с двумя неизвестными
Определение 1 . Пусть A – некоторое множество пар чисел (x ; y) . Говорят, что на множестве A задана числовая функция z от двух переменных x и y , если указано правило, с помощью которого каждой паре чисел из множества A ставится в соответствие некоторое число.
Задание числовой функции z от двух переменных x и y часто обозначают так:
| z = f (x , y) , | (1) |
причем в записи (1) числа x и y называют аргументами функции , а число z – значением функции , соответствующим паре аргументов (x ; y) .
Определение 2 . Нелинейным уравнением с двумя неизвестными x и y называют уравнение вида
| f (x , y) = 0 , | (2) |
где f (x , y) – любая функция, отличная от функции
где a , b , c – заданные числа.
Определение 3 . Решением уравнения (2) называют пару чисел (x ; y) , для которых формула (2) является верным равенством.
Пример 1 . Решить уравнение
| x 2 – 4xy + 6y 2 – – 12 y +18 = 0 . | (3) |
Решение . Преобразуем левую часть уравнения (3):
Таким образом, уравнение (3) можно переписать в виде
| (x – 2y) 2 + 2(y – 3) 2 = 0 . | (4) |
Поскольку квадрат любого числа неотрицателен, то из формулы (4) вытекает, что неизвестные x и y удовлетворяют системе уравнений
решением которой служит пара чисел (6 ; 3) .
Пример 2 . Решить уравнение
| sin (xy) = 2 . | (5) |
вытекает, что уравнение (5) решений не имеет.
Ответ : Решений нет.
Пример 3 . Решить уравнение
| ln (x – y) = 0 . | (6) |
Следовательно, решением уравнения (6) является бесконечное множество пар чисел вида
где y – любое число.
Видео:Решение системы уравнений с тремя переменнымиСкачать
Системы из двух уравнений, одно из которых линейное
Определение 4 . Решением системы уравнений
называют пару чисел (x ; y) , при подстановке которых в каждое из уравнений этой системы получается верное равенство.
Системы из двух уравнений, одно из которых линейное, имеют вид
где a , b , c – заданные числа, а g(x , y) – функция двух переменных x и y .
Пример 4 . Решить систему уравнений
| (7) |
Решение . Выразим из первого уравнения системы (7) неизвестное y через неизвестное x и подставим полученное выражение во второе уравнение системы:
Таким образом, решениями системы (7) являются две пары чисел
и
Ответ : (– 1 ; 9) , (9 ; – 1)
Видео:Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать
Однородные уравнения второй степени с двумя неизвестными
Определение 5 . Однородным уравнением второй степени с двумя неизвестными x и y называют уравнение вида
где a , b , c – заданные числа.
Пример 5 . Решить уравнение
| 3x 2 – 8xy + 5y 2 = 0 . | (8) |
Решение . Для каждого значения y рассмотрим уравнение (8) как квадратное уравнение относительно неизвестного x . Тогда дискриминант D квадратного уравнения (8) будет выражаться по формуле
откуда с помощью формулы для корней квадратного уравнения найдем корни уравнения (8):
Ответ . Решениями уравнения (8) являются все пары чисел вида
( y ; y) или
где y – любое число.
Следствие . Левую часть уравнения (8) можно разложить на множители
Видео:Нелинейные уравнения с двумя переменными и их геометрический смысл. 9 класс.Скачать
Системы из двух уравнений, одно из которых однородное
Системы из двух уравнений, одно из которых однородное, имеют вид
где a , b , c – заданные числа, а g(x , y) – функция двух переменных x и y .
Пример 6 . Решить систему уравнений
| (9) |
рассматривая его как квадратное уравнение относительно неизвестного x :
.
В случае, когда x = – y , из второго уравнения системы (9) получаем уравнение
корнями которого служат числа y1 = 2 , y2 = – 2 . Находя для каждого из этих значений y соответствующее ему значение x , получаем два решения системы: (– 2 ; 2) , (2 ; – 2) .
,
из второго уравнения системы (9) получаем уравнение
которое корней не имеет.
Ответ : (– 2 ; 2) , (2 ; – 2)
Видео:Матричный метод решения систем уравненийСкачать
Системы из двух уравнений, сводящиеся к системам, в которых одно из уравнений однородное
Пример 7 . Решить систему уравнений
| (10) |
Решение . Совершим над системой (10) следующие преобразования:
- второе уравнение системы оставим без изменений;
- к первому уравнению, умноженному на 5 , прибавим второе уравнение, умноженное на 3 , и запишем полученный результат вместо первого уравнения системы (10).
В результате система (10) преобразуется в равносильную ей систему (11), в которой первое уравнение является однородным уравнением:
| (11) |
рассматривая его как квадратное уравнение относительно неизвестного x :
.
В случае, когда x = – 5y , из второго уравнения системы (11) получаем уравнение
которое корней не имеет.
,
из второго уравнения системы (11) получаем уравнение
,
корнями которого служат числа y1 = 3 , y2 = – 3 . Находя для каждого из этих значений y соответствующее ему значение x , получаем два решения системы: (– 2 ; 3) , (2 ; – 3) .
Ответ : (– 2 ; 3) , (2 ; – 3)
Видео:Способы решения систем нелинейных уравнений. Практическая часть. 9 класс.Скачать
Примеры решения систем уравнений других видов
Пример 8 . Решить систему уравнений (МФТИ)
Решение . Введем новые неизвестные u и v , которые выражаются через x и y по формулам:
| (13) |
Для того, чтобы переписать систему (12) через новые неизвестные, выразим сначала неизвестные x и y через u и v . Из системы (13) следует, что
| (14) |
Решим линейную систему (14), исключив из второго уравнения этой системы переменную x . С этой целью совершим над системой (14) следующие преобразования:
- первое уравнение системы оставим без изменений;
- из второго уравнения вычтем первое уравнение и заменим второе уравнение системы на полученную разность.
В результате система (14) преобразуется в равносильную ей систему
из которой находим
| (15) |
Воспользовавшись формулами (13) и (15), перепишем исходную систему (12) в виде
| (16) |
У системы (16) первое уравнение – линейное, поэтому мы можем выразить из него неизвестное u через неизвестное v и подставить это выражение во второе уравнение системы:
Следовательно, решениями системы (16) являются две пары чисел
Из формул (13) вытекает, что , поэтому первое решение должно быть отброшено. В случае u2 = 5, v2 = 2 из формул (15) находим значения x и y :
Определение 6 . Решением системы из двух уравнений с тремя неизвестными называют тройку чисел (x ; y ; z) , при подстановке которых в каждое уравнение системы получается верное равенство.
Пример 9 . Решить систему из двух уравнений с тремя неизвестными
| (17) |
Решение . У системы (17) первое уравнение – линейное, поэтому мы можем выразить из него неизвестное z через неизвестные x и y и подставить это выражение во второе уравнение системы:
| (18) |
Перепишем второе уравнение системы (18) в другом виде:
Поскольку квадрат любого числа неотрицателен, то выполнение последнего равенства возможно лишь в случае x = 4, y = 4 .
Ответ : (4 ; 4 ; – 4)
Замечание . Рекомендуем посетителю нашего сайта, интересующемуся методами решения систем уравнений, ознакомиться также c разделом справочника «Системы линейных уравнений» и нашим учебным пособием «Системы уравнений».
📹 Видео
Математика | Система уравнений на желтую звездочку (feat Золотой Медалист по бегу)Скачать
Система НЕЛИНЕЙНЫХ уравнений ★ Как решать ★ Быстрый способ ★ Решите систему x^3+y^3=65; yx^2+xy^2=20Скачать
Как решить систему линейных уравнений с тремя неизвестными!?!Скачать
Неоднородная система линейных уравненийСкачать
Решение системы уравнений методом ГауссаСкачать
