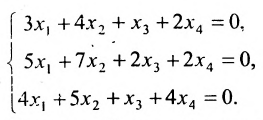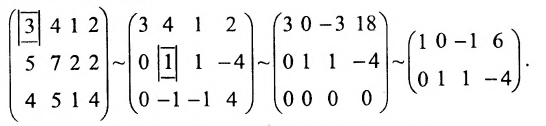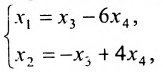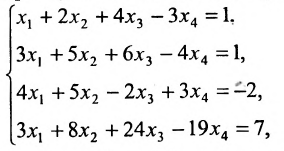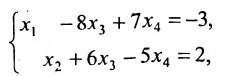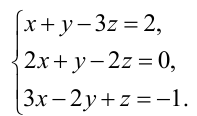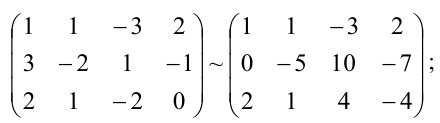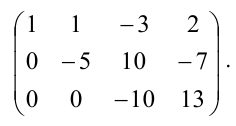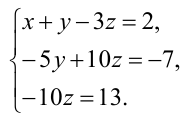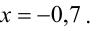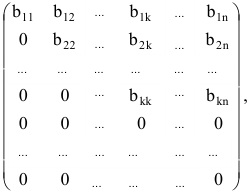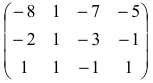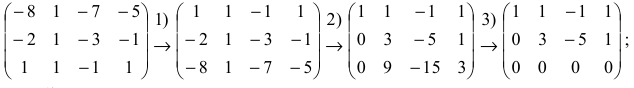Будут и задачи для самостоятельного решения, к которым можно посмотреть ответы.
- Понятие метода Гаусса
- Преимущества метода:
- Элементарные преобразования системы линейных уравнений
- Алгоритм и примеры решения методом Гаусса системы линейных уравнений с квадратной матрицей системы
- Решить систему линейных уравнений методом Гаусса самостоятельно, а затем посмотреть решение
- Решение методом Гаусса прикладных задач на примере задачи на сплавы
- Метод Гаусса и системы линейных уравнений, имеющие бесконечное множество решений
- Метод Гаусса и системы линейных уравнений, не имеющие решений
- Решить систему линейных уравнений методом Гаусса самостоятельно, а затем посмотреть решение
- Метод Гаусса и системы, в которых число неизвестных меньше числа уравнений
- Метод Гаусса и системы, в которых число неизвестных больше числа уравнений
- Метода Гаусса: примеры решения СЛАУ
- Метод Гаусса — что это такое?
- Основные определения и обозначения
- Описание алгоритма использования метода Гаусса для решения СЛАУ с равным количеством уравнений и неизвестных (обратный и прямой ход метода Гаусса)
- Описание алгоритма использования метода Гаусса для решения СЛАУ с несовпадающим количеством уравнений и неизвестных, или с вырожденной системой матрицы
- Метод Гаусса для чайников: примеры решений
- Что значит решить методом Гаусса?
- Матрицы, их свойства
- Определитель
- Классификация систем
- Элементарные преобразования
- Прибавление строки, умноженной на коэффициент
- В общем виде
- Когда нет решений
- Когда решений бесконечное количество
- Решение на конкретных примерах
- Пример неопределенной системы
- Пример несовместной системы
- Преимущества и недостатки метода
- Применение
- Метод Гаусса — определение и вычисление с примерами решения
- Алгоритм решения системы m линейных уравнений с n неизвестными методом Гаусса
- Исследование совместности и определённости системы. Теорема Кронекера-Капелли
- Однородные системы линейных уравнений
- Фундаментальная система решений. Общее решение неоднородной системы линейных уравнений
- Определение метода Гаусса
- Вычисление метода Гаусса
Видео:Математика без Ху!ни. Метод Гаусса.Скачать

Понятие метода Гаусса
Чтобы сразу же понять суть метода Гаусса, остановите ненадолго взгляд на анимации ниже. Почему одни буквы постепенно исчезают, другие окрашиваются в зелёный цвет, то есть становятся известными, а числа сменяются другими числами? Подсказка: из последнего уравнения совершенно точно известно, чему равна переменная z .
Догадались? В такой системе, называемой трапециевидной, последнее уравнение содержит только одну переменную и её значение можно однозначно найти. Затем значение этой переменной подставляют в предыдущее уравнение (обратный ход метода Гаусса, далее — просто обратный ход), из которого находят предыдущую переменную, и так далее.
Метод Гаусса, называемый также методом последовательного исключения неизвестных, состоит в следующем. При помощи элементарных преобразований систему линейных уравнений приводят к такому виду, чтобы её матрица из коэффициентов оказалась трапециевидной (то же самое, что треугольной или ступенчатой) или близкой к трапециевидной (прямой ход метода Гаусса, далее — просто прямой ход). Пример такой системы и её решения как раз и был приведён на анимации в начале урока.
В трапециевидной (треугольной) системе, как видим, третье уравнение уже не содержит переменных y и x , а второе уравнение — переменной x .
После того, как матрица системы приняла трапециевидную форму, уже не представляет труда разобраться в вопросе о совместности системы, определить число решений и найти сами решения.
У студентов наибольшие трудности вызывает именно прямой ход, то есть приведение исходной системы к трапециевидной. И это несмотря на то, что преобразования, которые необходимы для этого, называются элементарными. И называются неслучайно: в них требуется производить умножение (деление), сложение (вычитание) и перемену уравнений местами.
Преимущества метода:
- при решении систем линейных уравнений с числом уравнений и неизвестных более трёх метод Гаусса не такой громоздкий, как метод Крамера, поскольку при решении методом Гаусса необходимо меньше вычислений;
- методом Гаусса можно решать неопределённые системы линейных уравнений, то есть, имеющие общее решение (и мы разберём их на этом уроке), а, используя метод Крамера, можно лишь констатировать, что система неопределённа;
- можно решать системы линейных уравнений, в которых число неизвестных не равно числу уравнений (также разберём их на этом уроке);
- метод основан на элементарных (школьных) методах — методе подстановки неизвестных и методе сложения уравнений, которых мы коснулись в соответствующей статье.
Кроме того, метод Гаусса является основой одного из методов нахождения обратной матрицы.
Чтобы все прониклись простотой, с которой решаются трапециевидные (треугольные, ступенчатые) системы линейных уравнений, приведём решение такой системы с применением обратного хода. Быстрое решение этой системы было показано на картинке в начале урока.
Пример 1. Решить систему линейных уравнений, применяя обратный ход:
Решение. В данной трапециевидной системе переменная z однозначно находится из третьего уравнения. Подставляем её значение во второе уравнение и получаем значение переменой y:
Теперь нам известны значения уже двух переменных — z и y. Подставляем их в первое уравнение и получаем значение переменной x:
Из предыдущих шагов выписываем решение системы уравнений:
Чтобы получить такую трапециевидную систему линейных уравнений, которую мы решили очень просто, требуется применять прямой ход, связанный с элементарными преобразованиями системы линейных уравнений. Это также не очень сложно.
Видео:Решение системы уравнений методом ГауссаСкачать

Элементарные преобразования системы линейных уравнений
Повторяя школьный метод алгебраического сложения уравнений системы, мы выяснили, что к одному из уравнений системы можно прибавлять другое уравнение системы, причём каждое из уравнений может быть умножено на некоторые числа. В результате получаем систему линейных уравнений, эквивалентную данной. В ней уже одно уравнение содержало только одну переменную, подставляя значение которой в другие уравнений, мы приходим к решению. Такое сложение — один из видов элементарного преобразования системы. При использовании метода Гаусса можем пользоваться несколькими видами преобразований.
На анимации выше показано, как система уравнений постепенно превращается в трапециевидную. То есть такую, которую вы видели на самой первой анимации и сами убедились в том, что из неё просто найти значения всех неизвестных. О том, как выполнить такое превращение и, конечно, примеры, пойдёт речь далее.
При решении систем линейных уравнений с любым числом уравнений и неизвестных в системе уравнений и в расширенной матрице системы можно:
- переставлять местами строки (это и было упомянуто в самом начале этой статьи);
- если в результате других преобразований появились равные или пропорциональные строки, их можно удалить, кроме одной;
- удалять «нулевые» строки, где все коэффициенты равны нулю;
- любую строку умножать или делить на некоторое число;
- к любой строке прибавлять другую строку, умноженное на некоторое число.
В результате преобразований получаем систему линейных уравнений, эквивалентную данной.
Видео:Математика без Ху!ни. Метод Гаусса. Совместность системы. Ранг матрицы.Скачать

Алгоритм и примеры решения методом Гаусса системы линейных уравнений с квадратной матрицей системы
Рассмотрим сначала решение систем линейных уравений, в которых число неизвестных равно числу уравнений. Матрица такой системы — квадратная, то есть в ней число строк равно числу столбцов.
Пример 2. Решить методом Гаусса систему линейных уравнений
Решая системы линейных уравнений школьными способами, мы почленно умножали одно из уравнений на некоторое число, так, чтобы коэффициенты при первой переменной в двух уравнениях были противоположными числами. При сложении уравнений происходит исключение этой переменной. Аналогично действует и метод Гаусса.
Для упрощения внешнего вида решения составим расширенную матрицу системы:
В этой матрице слева до вертикальной черты расположены коэффициенты при неизвестных, а справа после вертикальной черты — свободные члены.
Для удобства деления коэффициентов при переменных (чтобы получить деление на единицу) переставим местами первую и вторую строки матрицы системы. Получим систему, эквивалентную данной, так как в системе линейных уравнений можно переставлять местами уравнения:
С помощью нового первого уравнения исключим переменную x из второго и всех последующих уравнений. Для этого ко второй строке матрицы прибавим первую строку, умноженную на 



Это возможно, так как
Если бы в нашей системе уравнений было больше трёх, то следовало бы прибавлять и ко всем последующим уравнениям первую строку, умноженную на отношение соответствующих коэффициентов, взятых со знаком минус.
В результате получим матрицу эквивалентную данной системе новой системы уравнений, в которой все уравнения, начиная со второго не содержат переменнную x:
Для упрощения второй строки полученной системы умножим её на 
Теперь, сохраняя первое уравнение полученной системы без изменений, с помощью второго уравнения исключаем переменную y из всех последующих уравнений. Для этого к третьей строке матрицы системы прибавим вторую строку, умноженную на 

Если бы в нашей системе уравнений было больше трёх, то следовало бы прибавлять и ко всем последующим уравнениям вторую строку, умноженную на отношение соответствующих коэффициентов, взятых со знаком минус.
В результате вновь получим матрицу системы, эквивалентной данной системе линейных уравнений:
Мы получили эквивалентную данной трапециевидную систему линейных уравнений:
Если число уравнений и переменных больше, чем в нашем примере, то процесс последовательного исключения переменных продолжается до тех пор, пока матрица системы не станет трапециевидной, как в нашем демо-примере.
Решение найдём «с конца» — обратный ход. Для этого из последнего уравнения определим z: 
Подставив это значение в предшествующее уравнение, найдём y:
Из первого уравнения найдём x:
Ответ: решение данной системы уравнений — 
Проверить решение системы можно и на калькуляторе, решающем методом Крамера: в этом случае будет выдан тот же ответ, если система имеет однозначное решение. Если же система имеет бесконечное множество решений, то таков будет и ответ, и это уже предмет пятой части этого урока.
Решить систему линейных уравнений методом Гаусса самостоятельно, а затем посмотреть решение
Пример 3. Решить систему линейных уравнений:
Перед нами вновь пример совместной и определённой системы линейных уравнений, в которой число уравнений равно числу неизвестных. Отличие от нашего демо-примера из алгоритма — здесь уже четыре уравнения и четыре неизвестных.
Пример 4. Решить систему линейных уравнений методом Гаусса:
Решение. Составляем расширенную матрицу системы. С помощью первого уравнения исключаем из последующих уравнений переменную 



Теперь нужно с помощью второго уравнения исключить переменную 
Проведём теперь собственно исключение переменной 


Теперь с помощью третьего уравнения исключим переменную 

Получили систему уравнений, которой эквивалентна заданная система:
Следовательно, полученная и данная системы являются совместными и определёнными. Окончательное решение находим «с конца». Из четвёртого уравнения непосредственно можем выразить значение переменной «икс четвёртое»:

Это значение подставляем в третье уравнение системы и получаем

откуда находим «икс третье»:

Далее, подставляем значения 



Наконец, подстановка значений


откуда находим «икс первое»:

Ответ: данная система уравнений имеет единственное решение 
Проверить решение системы можно и на калькуляторе, решающем методом Крамера: в этом случае будет выдан тот же ответ, если система имеет однозначное решение.
Видео:Метод Крамера за 3 минуты. Решение системы линейных уравнений - bezbotvyСкачать

Решение методом Гаусса прикладных задач на примере задачи на сплавы
Системы линейных уравнений применяются для моделирования реальных объектов физического мира. Решим одну из таких задач — на сплавы. Аналогичные задачи — задачи на смеси, стоимость или удельный вес отдельных товаров в группе товаров и тому подобные.
Пример 5. Три куска сплава имеют общую массу 150 кг. Первый сплав содержит 60% меди, второй — 30%, третий — 10%. При этом во втором и третьем сплавах вместе взятых меди на 28,4 кг меньше, чем в первом сплаве, а в третьем сплаве меди на 6,2 кг меньше, чем во втором. Найти массу каждого куска сплава.
Решение. Составляем систему линейных уравнений:
Умножаем второе и третье уравнения на 10, получаем эквивалентную систему линейных уравнений:
Составляем расширенную матрицу системы:
Внимание, прямой ход. Путём сложения (в нашем случае — вычитания) одной строки, умноженной на число (применяем два раза) с расширенной матрицей системы происходят следующие преобразования:
Прямой ход завершился. Получили расширенную матрицу трапециевидной формы.
Применяем обратный ход. Находим решение с конца. Видим, что 
Из второго уравнения находим

Из третьего уравнения —

Проверить решение системы можно и на калькуляторе, решающем методом Крамера: в этом случае будет выдан то же ответ, если система имеет однозначное решение.
О простоте метода Гаусса говорит хотя бы тот факт, что немецкому математику Карлу Фридриху Гауссу на его изобретение потребовалось лишь 15 минут. Кроме метода его имени из творчества Гаусса известно изречение «Не следует смешивать то, что нам кажется невероятным и неестественным, с абсолютно невозможным» — своего рода краткая инструкция по совершению открытий.
Во многих прикладных задачах может и не быть третьего ограничения, то есть, третьего уравнения, тогда приходится решать методом Гаусса систему двух уравнений с тремя неизвестными, или же, наоборот — неизвестных меньше, чем уравнений. К решению таких систем уравнений мы сейчас и приступим.
С помощью метода Гаусса можно установить, совместна или несовместна любая система n линейных уравнений с n переменными.
Видео:Решение системы уравнений методом Гаусса. Бесконечное множество решенийСкачать

Метод Гаусса и системы линейных уравнений, имеющие бесконечное множество решений
Следующий пример — совместная, но неопределённая система линейных уравнений, то есть имеющая бесконечное множество решений.
После выполнения преобразований в расширенной матрице системы (перестановки строк, умножения и деления строк на некоторое число, прибавлению к одной строке другой) могли появиться строки вида

соответствующие уравнению вида
Если во всех уравнениях имеющих вид
свободные члены равны нулю, то это означает, что система неопределённа, то есть имеет бесконечное множество решений, а уравнения этого вида – «лишние» и их исключаем из системы.
Пример 6. Решить методом Гаусса систему линейных уравнений:
Решение. Составим расширенную матрицу системы. Затем с помощью первого уравнения исключим переменную 

Теперь вторую строку прибавим к третьей и четвёртой.
В результате приходим к системе
Последние два уравнения превратились в уравнения вида 
Чтобы удовлетворить второму уравнению, мы можем для 






Как заданная, так и последняя системы совместны, но неопределённы, и формулы
при произвольных 

Видео:Система линейных уравнений. Общее решение. Метод ГауссаСкачать

Метод Гаусса и системы линейных уравнений, не имеющие решений
Следующий пример — несовместная система линейных уравнений, то есть не имеющая решений. Ответ на такие задачи так и формулируется: система не имеет решений.
Как уже говорилось в связи с первым примером, после выполнения преобразований в расширенной матрице системы могли появиться строки вида

соответствующие уравнению вида

Если среди них есть хотя бы одно уравнение с отличным от нуля свободным членом (т.е. 
Пример 7. Решить методом Гаусса систему линейных уравнений:
Решение. Составляем расширенную матрицу системы. С помощью первого уравнения исключаем из последующих уравнений переменную 



Теперь нужно с помощью второго уравнения исключить переменную 
Для исключения 


Теперь с помощью третьего уравнения исключим переменную 

Заданная система эквивалентна, таким образом, следующей:
Полученная система несовместна, так как её последнее уравнение 
Решить систему линейных уравнений методом Гаусса самостоятельно, а затем посмотреть решение
Пример 8. Решить систему линейных уравнений:
Видео:Решение системы линейных уравнений методом ГауссаСкачать

Метод Гаусса и системы, в которых число неизвестных меньше числа уравнений
Следующий пример — система линейных уравнений, в которой число неизвестных меньше числа уравнений.
Пример 9. Решить методом Гаусса систему линейных уравнений:
Решение. Составляем расширенную матрицу системы. С помощью первого уравнения исключаем из последующих уравнений переменную 




Теперь нужно с помощью второго уравнения исключить переменную 

Проведём теперь исключение переменной 


Четвёртая и третья строки — одинаковые, поэтому четвёртую исключаем из матрицы. А третью умножаем на 
Получили следующую систему уравнений, которой эквивалентна заданная система:




Ответ: данная система уравнений имеет единственное решение (1; 1; 1).
Видео:15. Однородная система линейных уравнений / фундаментальная система решенийСкачать

Метод Гаусса и системы, в которых число неизвестных больше числа уравнений
Следующий пример — система линейных уравнений, в которой число неизвестных больше числа уравнений.
Если при выполнении преобразований в расширенной матрице системы встретилось хотя бы одно уравнение вида

с равным нулю свободным членом, то в итоге получим эквивалентную исходной системе систему линейных уравнений, в которой число уравнений меньше числа переменных, а уравнения вида (*) удовлетворяются при любых значениях неизвестных. Их можно отбросить.
Неизвестным, которые удовлетворяли уравнению вида 0 = 0, например, третьему и четвёртому (*, отброшенным уравнениям), придадим произвольные значения (пример 2). Они чаще всего записываются так: 


Пример 10. Решить методом Гаусса систему линейных уравнений:
Решение. Составляем расширенную матрицу системы. Далее ко второй строке прибавляем первую, умноженную на 
Заданная система эквивалентна, таким образом, следующей:
В ней отсутствуют уравнения, дающие однозначные значения для 







Как заданная, так и последняя системы совместны, но неопределённы, и формулы
при произвольных 

Видео:Метод Гаусса решения систем линейных уравненийСкачать

Метода Гаусса: примеры решения СЛАУ
В данной статье мы:
- дадим определение методу Гаусса,
- разберем алгоритм действий при решении линейных уравнений, где количество уравнений совпадает c количеством неизвестных переменных, а определитель не равен нулю;
- разберем алгоритм действий при решении СЛАУ с прямоугольной или вырожденной матрицей.
Видео:12. Решение систем линейных уравнений методом ГауссаСкачать

Метод Гаусса — что это такое?
Метод Гаусса — это метод, который применяется при решении систем линейных алгебраических уравнений и имеет следующие преимущества:
- отсутствует необходимость проверять систему уравнений на совместность;
- есть возможность решать системы уравнений, где:
- количество определителей совпадает с количеством неизвестных переменных;
- количество определителей не совпадает с количеством неизвестных переменных;
- определитель равен нулю.
- результат выдается при сравнительно небольшом количестве вычислительных операций.
Видео:Неоднородная система линейных уравненийСкачать

Основные определения и обозначения
Есть система из р линейных уравнений с n неизвестными ( p может быть равно n ):
a 11 x 1 + a 12 x 2 + . . . + a 1 n x n = b 1 a 21 x 1 + a 22 x 2 + . . . + a 2 n x n = b 2 ⋯ a p 1 x 1 + a p 2 x 2 + . . . + a p n x n = b p ,
где x 1 , x 2 , . . . . , x n — неизвестные переменные, a i j , i = 1 , 2 . . . , p , j = 1 , 2 . . . , n — числа (действительные или комплексные), b 1 , b 2 , . . . , b n — свободные члены.
Если b 1 = b 2 = . . . = b n = 0 , то такую систему линейных уравнений называют однородной, если наоборот — неоднородной.
Решение СЛАУ — совокупность значения неизвестных переменных x 1 = a 1 , x 2 = a 2 , . . . , x n = a n , при которых все уравнения системы становятся тождественными друг другу.
Совместная СЛАУ — система, для которой существует хотя бы один вариант решения. В противном случае она называется несовместной.
Определенная СЛАУ — это такая система, которая имеет единственное решение. В случае, если решений больше одного, то такая система будет называться неопределенной.
Координатный вид записи:
a 11 x 1 + a 12 x 2 + . . . + a 1 n x n = b 1 a 21 x 1 + a 22 x 2 + . . . + a 2 n x n = b 2 ⋯ a p 1 x 1 + a p 2 x 2 + . . . + a p n x n = b p
Матричный вид записи: A X = B , где
A = a 11 a 12 ⋯ a 1 n a 21 a 22 ⋯ a 2 n ⋯ ⋯ ⋯ ⋯ a p 1 a p 2 ⋯ a p n — основная матрица СЛАУ;
X = x 1 x 2 ⋮ x n — матрица-столбец неизвестных переменных;
B = b 1 b 2 ⋮ b n — матрица свободных членов.
Расширенная матрица — матрица, которая получается при добавлении в качестве ( n + 1 ) столбца матрицу-столбец свободных членов и имеет обозначение Т .
T = a 11 a 12 ⋮ a 1 n b 1 a 21 a 22 ⋮ a 2 n b 2 ⋮ ⋮ ⋮ ⋮ ⋮ a p 1 a p 2 ⋮ a p n b n
Вырожденная квадратная матрица А — матрица, определитель которой равняется нулю. Если определитель не равен нулю, то такая матрица, а потом называется невырожденной.
Видео:метод Гаусса СИСТЕМА ЛИНЕЙНЫХ УРАВНЕНИЙ решение СЛАУСкачать

Описание алгоритма использования метода Гаусса для решения СЛАУ с равным количеством уравнений и неизвестных (обратный и прямой ход метода Гаусса)
Для начала разберемся с определениями прямого и обратного ходов метода Гаусса.
Прямой ход Гаусса — процесс последовательного исключения неизвестных.
Обратный ход Гаусса — процесс последовательного нахождения неизвестных от последнего уравнения к первому.
Алгоритм метода Гаусса:
Решаем систему из n линейных уравнений с n неизвестными переменными:
a 11 x 1 + a 12 x 2 + a 13 x 3 + . . . + a 1 n x n = b 1 a 21 x 1 + a 22 x 2 + a 23 x 3 + . . . + a 2 n x n = b 2 a 31 x 1 + a 32 x 2 + a 33 x 3 + . . . + a 3 n x n = b 3 ⋯ a n 1 x 1 + a n 2 x 2 + a n 3 x 3 + . . . + a n n x n = b n
Определитель матрицы не равен нулю.
- a 11 не равен нулю — всегда можно добиться этого перестановкой уравнений системы;
- исключаем переменную x 1 из всех уравнений систему, начиная со второго;
- прибавим ко второму уравнению системы первое, которое умножено на — a 21 a 11 , прибавим к третьему уравнению первое умноженное на — a 21 a 11 и т.д.
После проведенных действий матрица примет вид:
a 11 x 1 + a 12 x 2 + a 13 x 3 + . . . + a 1 n x n = b 1 a ( 1 ) 22 x 2 + a ( 1 ) 23 x 3 + . . . + a ( 1 ) 2 n x n = b ( 1 ) 2 a ( 1 ) 32 x 2 + a ( 1 ) 33 x 3 + . . . + a ( 1 ) 3 n x n = b ( 1 ) 3 ⋯ a ( 1 ) n 2 x 2 + a ( 1 ) n 3 x 3 + . . . + a ( 1 ) n n x n = b ( 1 ) n ,
где a i j ( 1 ) = a i j + a 1 j ( — a i 1 a 11 ) , i = 2 , 3 , . . . , n , j = 2 , 3 , . . . , n , b i ( 1 ) = b i + b 1 ( — a i 1 a 11 ) , i = 2 , 3 , . . . , n .
Далее производим аналогичные действия с выделенной частью системы:
a 11 x 1 + a 12 x 2 + a 13 x 3 + . . . + a 1 n x n = b 1 a ( 1 ) 22 x 2 + a ( 1 ) 23 x 3 + . . . + a ( 1 ) 2 n x n = b ( 1 ) 2 a ( 1 ) 32 x 2 + a ( 1 ) 33 x 3 + . . . + a ( 1 ) 3 n x n = b ( 1 ) 3 ⋯ a ( 1 ) n 2 x 2 + a ( 1 ) n 3 x 3 + . . . + a ( 1 ) n n x n = b ( 1 ) n
Считается, что a 22 ( 1 ) не равна нулю. Таким образом, приступаем к исключению неизвестной переменной x 2 из всех уравнений, начиная с третьего:
- к третьему уравнению систему прибавляем второе, которое умножено на — a ( 1 ) 42 a ( 1 ) 22 ;
- к четвертому прибавляем второе, которое умножено на — a ( 1 ) 42 a ( 1 ) 22 и т.д.
После таких манипуляций СЛАУ имеет следующий вид:
a 11 x 1 + a 12 x 2 + a 13 x 3 + . . . + a 1 n x n = b 1 a ( 1 ) 22 x 2 + a ( 1 ) 23 x 3 + . . . + a ( 1 ) 2 n x n = b ( 1 ) 2 a ( 2 ) 33 x 3 + . . . + a ( 2 ) 3 n x n = b ( 2 ) 3 ⋯ a ( 2 ) n 3 x 3 + . . . + a ( 2 ) n n x n = b ( 2 ) n ,
где a i j ( 2 ) = a ( 1 ) i j + a 2 j ( — a ( 1 ) i 2 a ( 1 ) 22 ) , i = 3 , 4 , . . . , n , j = 3 , 4 , . . . , n , b i ( 2 ) = b ( 1 ) i + b ( 1 ) 2 ( — a ( 1 ) i 2 a ( 1 ) 22 ) , i = 3 , 4 , . . . , n . .
Таким образом, переменная x 2 исключена из всех уравнений, начиная с третьего.
Далее приступаем к исключению неизвестной x 3 , действуя по аналоги с предыдущим образцом:
a 11 x 1 + a 12 x 2 + a 13 x 3 + . . . + a 1 n x n = b 1 a ( 1 ) 22 x 2 + a ( 1 ) 23 x 3 + . . . + a ( 1 ) 2 n x n = b ( 1 ) 2 a ( 2 ) 33 x 3 + . . . + a ( 2 ) 3 n x n = b ( 2 ) 3 ⋯ a ( n — 1 ) n n x n = b ( n — 1 ) n
После того как система приняла такой вид, можно начать обратный ход метода Гаусса:
- вычисляем x n из последнего уравнения как x n = b n ( n — 1 ) a n n ( n — 1 ) ;
- с помощью полученного x n находим x n — 1 из предпоследнего уравнения и т.д., находим x 1 из первого уравнения.
Найти решение системы уравнений методом Гаусса:
3 x 1 + 2 x 2 + x 3 + x 4 = — 2 x 1 — x 2 + 4 x 3 — x 4 = — 1 — 2 x 1 — 2 x 2 — 3 x 3 + x 4 = 9 x 1 + 5 x 2 — x 3 + 2 x 4 = 4
Коэффициент a 11 отличен от нуля, поэтому приступаем к прямому ходу решения, т.е. к исключению переменной x 11 из всех уравнений системы, кроме первого. Для того, чтобы это сделать, прибавляем к левой и правой частям 2-го, 3-го и 4-го уравнений левую и правую часть первого, которая умножена на — a 21 a 11 :
— 1 3 , — а 31 а 11 = — — 2 3 = 2 3 и — а 41 а 11 = — 1 3 .
3 x 1 + 2 x 2 + x 3 + x 4 = — 2 x 1 — x 2 + 4 x 3 — x 4 = — 1 — 2 x 1 — 2 x 2 — 3 x 3 + x 4 = 9 x 1 + 5 x 2 — x 3 + 2 x 4 = 4 ⇔
⇔ 3 x 1 + 2 x 2 + x 3 + x 4 = — 2 x 1 — x 2 + 4 x 3 — x 4 + ( — 1 3 ) ( 3 x 1 + 2 x 2 + x 3 + x 4 ) = — 1 + ( — 1 3 ) ( — 2 ) — 2 x 1 — 2 x 2 — 3 x 3 + x 4 + 2 3 ( 3 x 1 + 2 x 2 + x 3 + x 4 ) = 9 + 2 3 ( — 2 ) x 1 + 5 x 2 — x 3 + 2 x 4 + ( — 1 3 ) ( 3 x 1 + 2 x 2 + x 3 + x 4 ) = 4 + ( — 1 3 ) ( — 2 ) ⇔
⇔ 3 x 1 + 2 x 2 + x 3 + x 4 = — 2 — 5 3 x 2 + 11 3 x 3 — 4 3 x 4 = — 1 3 — 2 3 x 2 — 7 3 x 3 + 5 3 x 4 = 23 3 13 3 x 2 — 4 3 x 3 + 5 3 x 4 = 14 3
Мы исключили неизвестную переменную x 1 , теперь приступаем к исключению переменной x 2 :
— a 32 ( 1 ) a 22 ( 1 ) = — — 2 3 — 5 3 = — 2 5 и а 42 ( 1 ) а 22 ( 1 ) = — 13 3 — 5 3 = 13 5 :
3 x 1 + 2 x 2 + x 3 + x 4 = — 2 — 5 3 x 2 + 11 3 x 3 — 4 3 x 4 = — 1 3 — 2 3 x 2 — 7 3 x 3 + 5 3 x 4 = 23 3 13 3 x 2 — 4 3 x 3 + 5 3 x 4 = 14 3 ⇔
⇔ 3 x 1 + 2 x 2 + x 3 + x 4 = — 2 — 5 3 x 2 + 11 3 x 3 — 4 3 x 4 = — 1 3 — 2 3 x 2 — 7 3 x 3 + 5 3 x 4 + ( — 2 5 ) ( — 5 3 x 2 + 11 3 x 3 — 4 3 x 4 ) = 23 3 + ( — 2 5 ) ( — 1 3 ) 13 3 x 2 — 4 3 x 3 + 5 3 x 4 + 13 5 ( — 5 3 x 2 + 11 3 x 3 — 4 3 x 4 ) = 14 3 + 13 5 ( — 1 3 ) ⇔
⇔ 3 x 1 + 2 x 2 + x 3 + x 4 = — 2 — 5 3 x 2 + 11 3 x 3 — 4 3 x 4 = — 1 3 — 19 5 x 3 + 11 5 x 4 = 39 5 41 5 x 3 — 9 5 x 4 = 19 5
Для того чтобы завершить прямой ход метода Гаусса, необходимо исключить x 3 из последнего уравнения системы — а 43 ( 2 ) а 33 ( 2 ) = — 41 5 — 19 5 = 41 19 :
3 x 1 + 2 x 2 + x 3 + x 4 = — 2 — 5 3 x 2 + 11 3 x 3 — 4 3 x 4 = — 1 3 — 19 5 x 3 + 11 5 x 4 = 39 5 41 5 x 3 — 9 5 x 4 = 19 5 ⇔
3 x 1 + 2 x 2 + x 3 + x 4 = — 2 — 5 3 x 2 + 11 3 x 3 — 4 3 x 4 = — 1 3 — 19 5 x 3 + 11 5 x 4 = 39 5 41 5 x 3 — 9 5 x 4 + 41 19 ( — 19 5 x 3 + 11 5 x 4 ) = 19 5 + 41 19 39 5 ⇔
⇔ 3 x 1 + 2 x 2 + x 3 + x 4 = — 2 — 5 3 x 2 + 11 3 x 3 — 4 3 x 4 = — 1 3 — 19 5 x 3 + 11 5 x 4 = 39 5 56 19 x 4 = 392 19
Обратный ход метода Гаусса:
- из последнего уравнения имеем: x 4 = 392 19 56 19 = 7 ;
- из 3-го уравнения получаем: x 3 = — 5 19 ( 39 5 — 11 5 x 4 ) = — 5 19 ( 39 5 — 11 5 × 7 ) = 38 19 = 2 ;
- из 2-го: x 2 = — 3 5 ( — 1 3 — 11 3 x 4 + 4 3 x 4 ) = — 3 5 ( — 1 3 — 11 3 × 2 + 4 3 × 7 ) = — 1 ;
- из 1-го: x 1 = 1 3 ( — 2 — 2 x 2 — x 3 — x 4 ) = — 2 — 2 × ( — 1 ) — 2 — 7 3 = — 9 3 = — 3 .
Ответ: x 1 = — 3 ; x 2 = — 1 ; x 3 = 2 ; x 4 = 7
Найти решение этого же примера методом Гаусса в матричной форме записи:
3 x 1 + 2 x 2 + x 3 + x 4 = — 2 x 1 — x 2 + 4 x 3 — x 4 = — 1 — 2 x 1 — 2 x 2 — 3 x 3 + x 4 = 9 x 1 + 5 x 2 — x 3 + 2 x 4 = 4
Расширенная матрица системы представлена в виде:
x 1 x 2 x 3 x 4 3 2 1 1 1 — 1 4 — 1 — 2 — 2 — 3 1 1 5 — 1 2 — 2 — 1 9 4
Прямой ход метода Гаусса в данном случае предполагает приведение расширенной матрицы к трапецеидальному виду при помощи элементарных преобразований. Этот процесс очень поход на процесс исключения неизвестных переменных в координатном виде.
Преобразование матрицы начинается с превращения всех элементов нулевые. Для этого к элементам 2-ой, 3-ей и 4-ой строк прибавляем соответствующие элементы 1-ой строки, которые умножены на — a 21 a 11 = — 1 3 , — a 31 a 11 = — — 2 3 = 2 3 и н а — а 41 а 11 = — 1 3 .
Дальнейшие преобразования происходит по такой схеме: все элементы во 2-ом столбце, начиная с 3-ей строки, становятся нулевыми. Такой процесс соответствует процессу исключения переменной . Для того, чтобы выполнить этой действие, необходимо к элементам 3-ей и 4-ой строк прибавить соответствующие элементы 1-ой строки матрицы, которая умножена на — а 32 ( 1 ) а 22 ( 1 ) = — 2 3 — 5 3 = — 2 5 и — а 42 ( 1 ) а 22 ( 1 ) = — 13 3 — 5 3 = 13 5 :
x 1 x 2 x 3 x 4 3 2 1 1 | — 2 0 — 5 3 11 3 — 4 3 | — 1 3 0 — 2 3 — 7 3 5 3 | 23 3 0 13 3 — 4 3 5 3 | 14 3
x 1 x 2 x 3 x 4
3 2 1 1 | — 2 0 — 5 3 11 3 — 4 3 | — 1 3 0 — 2 3 + ( — 2 5 ) ( — 5 3 ) — 7 3 + ( — 2 5 ) 11 3 5 3 + ( — 2 5 ) ( — 4 3 ) | 23 3 + ( — 2 5 ) ( — 1 3 ) 0 13 3 + 13 5 ( — 5 3 ) — 4 3 + 13 5 × 11 3 5 3 + 13 5 ( — 4 3 ) | 14 3 + 13 5 ( — 1 3 )
x 1 x 2 x 3 x 4
3 2 1 1 | — 2 0 — 5 3 11 3 — 4 3 | — 1 3 0 0 — 19 5 11 5 | 39 5 0 0 41 5 — 9 5 | 19 5
Теперь исключаем переменную x 3 из последнего уравнения — прибавляем к элементам последней строки матрицы соответствующие элементы последней строки, которая умножена на а 43 ( 2 ) а 33 ( 2 ) = — 41 5 — 19 5 = 41 19 .
x 1 x 2 x 3 x 4 3 2 1 1 | — 2 0 — 5 3 11 3 — 4 3 | — 1 3 0 0 — 19 5 11 5 | 39 5 0 0 41 5 — 9 5 | 19 5
x 1 x 2 x 3 x 4
3 2 1 1 | — 2 0 — 5 3 11 3 — 4 3 | — 1 3 0 0 — 19 5 11 5 | 39 5 0 0 41 5 + 41 19 ( — 19 5 ) — 9 5 + 41 19 × 11 5 | 19 5 + 41 19 × 39 5
x 1 x 2 x 3 x 4
3 2 1 1 | — 2 0 — 5 3 11 3 — 4 3 | — 1 3 0 0 — 19 5 11 5 | 39 5 0 0 0 56 19 | 392 19
Теперь применим обратных ход метода. В матричной форме записи такое преобразование матрицы, чтобы матрица, которая отмечена цветом на изображении:
x 1 x 2 x 3 x 4 3 2 1 1 | — 2 0 — 5 3 11 3 — 4 3 | — 1 3 0 0 — 19 5 11 5 | 39 5 0 0 0 56 19 | 392 19
стала диагональной, т.е. приняла следующий вид:
x 1 x 2 x 3 x 4 3 0 0 0 | а 1 0 — 5 3 0 0 | а 2 0 0 — 19 5 0 | а 3 0 0 0 56 19 | 392 19 , где а 1 , а 2 , а 3 — некоторые числа.
Такие преобразования выступают аналогом прямому ходу, только преобразования выполняются не от 1-ой строки уравнения, а от последней. Прибавляем к элементам 3-ей, 2-ой и 1-ой строк соответствующие элементы последней строки, которая умножена на
— 11 5 56 19 = — 209 280 , н а — — 4 3 56 19 = 19 42 и н а — 1 56 19 = 19 56 .
x 1 x 2 x 3 x 4 3 2 1 1 | — 2 0 — 5 3 11 3 — 4 3 | — 1 3 0 0 — 19 5 11 5 | 39 5 0 0 0 56 19 | 392 19
x 1 x 2 x 3 x 4
3 2 1 1 + ( — 19 56 ) 56 19 | — 2 + ( — 19 56 ) 392 19 0 — 5 3 11 3 — 4 3 + 19 42 × 56 19 | — 1 3 + 19 42 × 392 19 0 0 — 19 5 11 5 + ( — 209 280 ) 56 19 | 39 5 + ( — 209 280 ) 392 19 0 0 0 56 19 | 392 19
x 1 x 2 x 3 x 4
3 2 1 0 | — 9 0 — 5 3 11 3 0 | 9 0 0 — 19 5 0 | — 38 5 0 0 0 56 19 | 392 19
Далее прибавляем к элементам 2-ой и 1-ой строк соответствующие элементы 3-ей строки, которые умножены на
— 11 3 — 19 5 = 55 57 и н а — 1 — 19 5 = 5 19 .
x 1 x 2 x 3 x 4 3 2 1 0 | — 9 0 — 5 3 11 3 0 | 9 0 0 — 19 5 0 | — 38 5 0 0 0 56 19 | 392 19
x 1 x 2 x 3 x 4
3 2 1 + 5 19 ( — 19 5 ) 0 | — 9 + 5 19 ( — 38 5 ) 0 — 5 3 11 3 + 55 57 ( — 19 5 ) 0 | 9 + 55 57 ( — 38 5 ) 0 0 — 19 5 0 | — 38 5 0 0 0 56 19 | 392 19
x 1 x 2 x 3 x 4
3 2 1 0 | — 11 0 — 5 3 0 0 | 5 3 0 0 — 19 5 0 | — 38 5 0 0 0 56 19 | 392 19
На последнем этапе прибавляем элементы 2-ой строки к соответствующим элементам 1-ой строки, которые умножены на — 2 — 5 3 = 6 5 .
x 1 x 2 x 3 x 4 3 2 1 0 | — 11 0 — 5 3 0 0 | 5 3 0 0 — 19 5 0 | — 38 5 0 0 0 56 19 | 392 19
x 1 x 2 x 3 x 4
3 2 + 6 5 ( — 5 3 ) 0 0 | — 11 + 6 5 × 5 3 ) 0 — 5 3 0 0 | 5 3 0 0 — 19 5 0 | — 38 5 0 0 0 56 19 | 392 19
x 1 x 2 x 3 x 4
3 0 0 0 | — 9 0 — 5 3 0 0 | 5 3 0 0 — 19 5 0 | — 38 5 0 0 0 56 19 | 392 19
Полученная матрица соответствует системе уравнений
3 x 1 = — 9 — 5 3 x 2 = 5 3 — 19 5 x 3 = — 38 5 56 19 x 4 = 392 19 , откуда находим неизвестные переменные.
Ответ: x 1 = — 3 , x 2 = — 1 , x 3 = 2 , x 4 = 7 .
Видео:14. Метод Гаусса решения систем линейных уравнений ( бесконечное множество решений ). Часть 3Скачать

Описание алгоритма использования метода Гаусса для решения СЛАУ с несовпадающим количеством уравнений и неизвестных, или с вырожденной системой матрицы
Если основная матрица квадратная или прямоугольная, то системы уравнений могут иметь единственное решение, могут не иметь решений, а могут иметь бесконечное множество решений.
Из данного раздела мы узнаем, как с помощью метода Гаусса определить совместность или несовместность СЛАУ, а также, в случае совместности, определить количество решений для системы.
В принципе, метод исключения неизвестных при таких СЛАУ остается таким же, однако есть несколько моментов, на которых необходимо заострить внимание.
На некоторых этапах исключения неизвестных, некоторые уравнения обращаются в тождества 0=0. В таком случае, уравнения можно смело убрать из системы и продолжить прямой ход метода Гаусса.
Если мы исключаем из 2-го и 3-го уравнения x 1 , то ситуация оказывается следующей:
x 1 + 2 x 2 — x 3 + 3 x 4 = 7 2 x 1 + 4 x 2 — 2 x 3 + 6 x 4 = 14 x — x + 3 x + x = — 1 ⇔
x 1 + 2 x 2 — x 3 + 3 x 4 = 7 2 x 1 + 4 x 2 — 2 x 3 + 6 x 4 + ( — 2 ) ( x 1 + 2 x 2 — x 3 + 3 x 4 ) = 14 + ( — 2 ) × 7 x — x + 3 x + x + ( — 1 ) ( x 1 + 2 x 2 — x 3 + 3 x 4 ) = — 1 + ( — 1 ) × 7 ⇔
⇔ x 1 + 2 x 2 — x 3 + 3 x 4 = 7 0 = 0 — 3 x 2 + 4 x 3 — 2 x 4 = — 8
Из этого следует, что 2-ое уравнение можно смело удалять из системы и продолжать решение.
Если мы проводим прямой ход метода Гаусса, то одно или несколько уравнений может принять вид — некоторое число, которое отлично от нуля.
Это свидетельствует о том, что уравнение, обратившееся в равенство 0 = λ , не может обратиться в равенство ни при каких любых значениях переменных. Проще говоря, такая система несовместна (не имеет решения).
- В случае если при проведении прямого хода метода Гаусса одно или несколько уравнений принимают вид 0 = λ , где λ — некоторое число, которое отлично от нуля, то система несовместна.
- Если же в конце прямого хода метода Гаусса получается система, число уравнений которой совпадает с количеством неизвестных, то такая система совместна и определена: имеет единственное решение, которое вычисляется обратным ходом метода Гаусса.
- Если при завершении прямого хода метода Гаусса число уравнений в системе оказывается меньше количества неизвестных, то такая система совместна и имеет бесконечно количество решений, которые вычисляются при обратном ходе метода Гаусса.
Видео:Решение системы уравнений методом Гаусса 4x4Скачать

Метод Гаусса для чайников: примеры решений



В данной статье метод рассматривается как способ решения систем линейных уравнений (СЛАУ). Метод является аналитическим, то есть позволяет написать алгоритм решения в общем виде, а потом уже подставлять туда значения из конкретных примеров. В отличие от матричного метода или формул Крамера, при решении системы линейных уравнений методом Гаусса можно работать и с теми, что имеют решений бесконечно много. Или не имеют его вовсе.
Видео:Крамера. Гаусса. Матричный метод. Система линейных уравнений. 3 способа решенияСкачать

Что значит решить методом Гаусса?
Для начала необходимо нашу систему уравнений записать в виде матрицы. Выглядит это следующим образом. Берется система:
Коэффициенты записываются в виде таблицы, а справа отдельным столбиком — свободные члены. Столбец со свободными членами отделяется для удобства вертикальной чертой. Матрица, включающая в себя этот столбец, называется расширенной.
Далее основную матрицу с коэффициентами нужно привести к верхней треугольной форме. Это основной момент решения системы методом Гаусса. Проще говоря, после определенных манипуляций матрица должна выглядеть так, чтобы в ее левой нижней части стояли одни нули:
Тогда, если записать новую матрицу опять как систему уравнений, можно заметить, что в последней строке уже содержится значение одного из корней, которое затем подставляется в уравнение выше, находится еще один корень, и так далее.
Это описание решения методом Гаусса в самых общих чертах. А что получится, если вдруг у системы нет решения? Или их бесконечно много? Чтобы ответить на эти и еще множество вопросов, необходимо рассмотреть отдельно все элементы, использующиеся при решении методом Гаусса.
Видео:12. Метод Гаусса решения систем линейных уравнений. Часть 1.Скачать

Матрицы, их свойства
Никакого скрытого смысла в матрице нет. Это просто удобный способ записи данных для последующих операций с ними. Бояться их не надо даже школьникам.
Матрица всегда прямоугольная, потому что так удобнее. Даже в методе Гаусса, где все сводится к построению матрицы треугольного вида, в записи фигурирует прямоугольник, только с нулями на том месте, где нет чисел. Нули можно не записывать, но они подразумеваются.
Матрица имеет размер. Ее «ширина» — число строк (m), «длина» — число столбцов (n). Тогда размер матрицы A (для их обозначения обычно используются заглавные латинские буквы) будет обозначаться как Am×n. Если m=n, то эта матрица квадратная, и m=n — ее порядок. Соответственно, любой элемент матрицы A можно обозначить через номер его строки и столбца: axy; x — номер строки, изменяется [1, m], y — номер столбца, изменяется [1, n].
В методе Гаусса матрицы — это не основной момент решения. В принципе, все операции можно выполнять непосредственно с самими уравнениями, однако запись получится куда более громоздкая, и в ней будет гораздо легче запутаться.
Видео:Исследовать систему уравнений на совместность и решить методом Гаусса и методом обратной матрицыСкачать

Определитель
Еще у матрицы есть определитель. Это очень важная характеристика. Выяснять его смысл сейчас не стоит, можно просто показать, как он вычисляется, а потом рассказать, какие свойства матрицы он определяет. Наиболее простой способ нахождения определителя — через диагонали. В матрице проводятся воображаемые диагонали; элементы, находящиеся на каждой из них, перемножаются, а затем полученные произведения складываются: диагонали с наклоном вправо — со знаком «плюс», с наклоном влево — со знаком «минус».
Крайне важно отметить, что вычислять определитель можно только у квадратной матрицы. Для прямоугольной матрицы можно сделать следующее: из количества строк и количества столбцов выбрать наименьшее (пусть это будет k), а затем в матрице произвольным образом отметить k столбцов и k строк. Элементы, находящиеся на пересечении выбранных столбцов и строк, составят новую квадратную матрицу. Если определитель такой матрицы будет числом, отличным от нуля, то назовется базисным минором первоначальной прямоугольной матрицы.
Перед тем как приступить к решению системы уравнений методом Гаусса, не мешает посчитать определитель. Если он окажется нулевым, то сразу можно говорить, что у матрицы количество решений либо бесконечно, либо их вообще нет. В таком печальном случае надо идти дальше и узнавать про ранг матрицы.
Видео:Система уравнений не имеет решений или имеет бесчисленное множество решенийСкачать

Классификация систем
Существует такое понятие, как ранг матрицы. Это максимальный порядок ее определителя, отличного от нуля (если вспомнить про базисный минор, можно сказать, что ранг матрицы — порядок базисного минора).
По тому, как обстоят дела с рангом, СЛАУ можно разделить на:
- Совместные. У совместных систем ранг основной матрицы (состоящей только из коэффициентов) совпадает с рангом расширенной (со столбцом свободных членов). Такие системы имеют решение, но необязательно одно, поэтому дополнительно совместные системы делят на:
- — определенные — имеющие единственное решение. В определенных системах равны ранг матрицы и количество неизвестных (или число столбцов, что есть одно и то же);
- — неопределенные — с бесконечным количеством решений. Ранг матриц у таких систем меньше количества неизвестных.
- Несовместные. У таких систем ранги основной и расширенной матриц не совпадают. Несовместные системы решения не имеют.
Метод Гаусса хорош тем, что позволяет в ходе решения получить либо однозначное доказательство несовместности системы (без вычисления определителей больших матриц), либо решение в общем виде для системы с бесконечным числом решений.
Видео:Метод Гаусса Пример РешенияСкачать

Элементарные преобразования
До того как приступить непосредственно к решению системы, можно сделать ее менее громоздкой и более удобной для вычислений. Это достигается за счет элементарных преобразований — таких, что их выполнение никак не меняет конечный ответ. Следует отметить, что некоторые из приведенных элементарных преобразований действительны только для матриц, исходниками которых послужили именно СЛАУ. Вот список этих преобразований:
- Перестановка строк. Очевидно, что если в записи системы поменять порядок уравнений, то на решение это никак не повлияет. Следовательно, в матрице этой системы также можно менять местами строки, не забывая, конечно, про столбец свободных членов.
- Умножение всех элементов строки на некоторый коэффициент. Очень полезно! С помощью него можно сократить большие числа в матрице или убрать нули. Множество решений, как обычно, не изменится, а выполнять дальнейшие операции станет удобнее. Главное, чтобы коэффициент не был равен нулю.
- Удаление строк с пропорциональными коэффициентами. Это отчасти следует из предыдущего пункта. Если две или более строки в матрице имеют пропорциональные коэффициенты, то при умножении/делении одной из строк на коэффициент пропорциональности получаются две (или, опять же, более) абсолютно одинаковые строки, и можно убрать лишние, оставив только одну.
- Удаление нулевой строки. Если в ходе преобразований где-то получилась строка, в которой все элементы, включая свободный член, — ноль, то такую строку можно назвать нулевой и выкинуть из матрицы.
- Прибавление к элементам одной строки элементов другой (по соответствующим столбцам), умноженных на некоторый коэффициент. Самое неочевидное и самое важное преобразование из всех. На нем стоит остановиться поподробнее.
Видео:ФСР. Система однородных уравнений. Общее решениеСкачать

Прибавление строки, умноженной на коэффициент
Для простоты понимания стоит разобрать этот процесс по шагам. Берутся две строки из матрицы:
Допустим, необходимо ко второй прибавить первую, умноженную на коэффициент «-2».
Затем в матрице вторая строка заменяется на новую, а первая остается без изменений.
Необходимо заметить, что коэффициент умножения можно подобрать таким образом, чтобы в результате сложения двух строк один из элементов новой строки был равен нулю. Следовательно, можно получить уравнение в системе, где на одну неизвестную будет меньше. А если получить два таких уравнения, то операцию можно проделать еще раз и получить уравнение, которое будет содержать уже на две неизвестных меньше. А если каждый раз превращать в ноль один коэффициент у всех строк, что стоят ниже исходной, то можно, как по ступенькам, спуститься до самого низа матрицы и получить уравнение с одной неизвестной. Это и называется решить систему методом Гаусса.
В общем виде
Пусть существует система. Она имеет m уравнений и n корней-неизвестных. Записать ее можно следующим образом:
Из коэффициентов системы составляется основная матрица. В расширенную матрицу добавляется столбец свободных членов и для удобства отделяется чертой.
- первая строка матрицы умножается на коэффициент k = (-a21/a11);
- первая измененная строка и вторая строка матрицы складываются;
- вместо второй строки в матрицу вставляется результат сложения из предыдущего пункта;
- теперь первый коэффициент в новой второй строке равен a11 × (-a21/a11) + a21 = -a21 + a21 = 0.
Теперь выполняется та же серия преобразований, только участвуют первая и третья строки. Соответственно, в каждом шаге алгоритма элемент a21 заменяется на a31. Потом все повторяется для a41, . am1. В итоге получается матрица, где в строках [2, m] первый элемент равен нулю. Теперь нужно забыть о строке номер один и выполнить тот же алгоритм, начиная со второй строки:
- коэффициент k = (-a32/a22);
- с «текущей» строкой складывается вторая измененная строка;
- результат сложения подставляется в третью, четвертую и так далее строки, а первая и вторая остаются неизменными;
- в строках [3, m] матрицы уже два первых элемента равны нулю.
Алгоритм надо повторять, пока не появится коэффициент k = (-am,m-1/amm). Это значит, что в последний раз алгоритм выполнялся только для нижнего уравнения. Теперь матрица похожа на треугольник, или имеет ступенчатую форму. В нижней строчке имеется равенство amn × xn = bm. Коэффициент и свободный член известны, и корень выражается через них: xn = bm/amn. Полученный корень подставляется в верхнюю строку, чтобы найти xn-1 = (bm-1 — am-1,n×(bm/amn))÷am-1,n-1. И так далее по аналогии: в каждой следующей строке находится новый корень, и, добравшись до «верха» системы, можно отыскать множество решений [x1, . xn]. Оно будет единственным.
Когда нет решений
Если в одной из матричных строк все элементы, кроме свободного члена, равны нулю, то уравнение, соответствующее этой строке, выглядит как 0 = b. Оно не имеет решения. И поскольку такое уравнение заключено в систему, то и множество решений всей системы — пустое, то есть она является вырожденной.
Когда решений бесконечное количество
Может получиться так, что в приведенной треугольной матрице нет строк с одним элементом-коэффициентом уравнения, и одним — свободным членом. Есть только такие строки, которые при переписывании имели бы вид уравнения с двумя или более переменными. Значит, у системы имеется бесконечное число решений. В таком случае ответ можно дать в виде общего решения. Как это сделать?
Все переменные в матрице делятся на базисные и свободные. Базисные — это те, которые стоят «с краю» строк в ступенчатой матрице. Остальные — свободные. В общем решении базисные переменные записываются через свободные.
Для удобства матрица сначала переписывается обратно в систему уравнений. Потом в последнем из них, там, где точно осталась только одна базисная переменная, она остается с одной стороны, а все остальное переносится в другую. Так делается для каждого уравнения с одной базисной переменной. Потом в остальные уравнения, там, где это возможно, вместо базисной переменной подставляется полученное для нее выражение. Если в результате опять появилось выражение, содержащее только одну базисную переменную, она оттуда опять выражается, и так далее, пока каждая базисная переменная не будет записана в виде выражения со свободными переменными. Это и есть общее решение СЛАУ.
Можно также найти базисное решение системы — дать свободным переменным любые значения, а потом для этого конкретного случая посчитать значения базисных переменных. Частных решений можно привести бесконечно много.
Решение на конкретных примерах
Вот система уравнений.
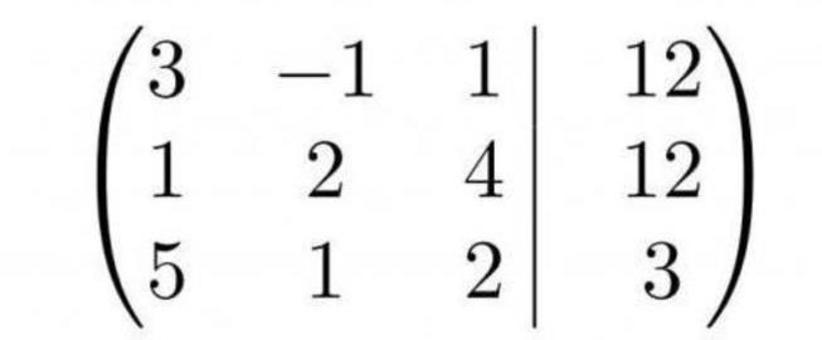
Для удобства лучше сразу составить ее матрицу
Известно, что при решении методом Гаусса уравнение, соответствующее первой строке, в конце преобразований останется неизменным. Поэтому выгодней будет, если левый верхний элемент матрицы будет наименьшим — тогда первые элементы остальных строк после операций обратятся в ноль. Значит, в составленной матрице выгодно будет на место первой строки поставить вторую.
Далее необходимо так изменить вторую и третью строки, чтобы первые элементы стали нулями. Для этого надо сложить их с первой, умноженной их на коэффициент:
Теперь, чтобы не запутаться, необходимо записать матрицу с промежуточными результатами преобразований.
Очевидно, что такую матрицу можно сделать более удобной для восприятия с помощью некоторых операций. Например, из второй строки можно убрать все «минусы», умножая каждый элемент на «-1».
Стоит также заметить, что в третьей строке все элементы кратны трем. Тогда можно сократить строку на это число, умножая каждый элемент на «-1/3» (минус — заодно, чтобы убрать отрицательные значения).
Выглядит гораздо приятнее. Теперь надо оставить в покое первую строку и поработать со второй и третьей. Задача — прибавить к третьей строке вторую, умноженную на такой коэффициент, чтобы элемент a32 стал равен нулю.
k = (-a32/a22) = (-3/7) = -3/7 (если в ходе некоторых преобразований в ответе получилось не целое число, рекомендуется для соблюдения точности вычислений оставить его «как есть», в виде обыкновенной дроби, а уже потом, когда получены ответы, решать, стоит ли округлять и переводить в другую форму записи)
Снова записывается матрица с новыми значениями.
| 1 | 2 | 4 | 12 |
| 0 | 7 | 11 | 24 |
| 0 | 0 | -9/7 | -61/7 |
Как видно, полученная матрица уже имеет ступенчатый вид. Поэтому дальнейшие преобразования системы по методу Гаусса не требуются. Что здесь можно сделать, так это убрать из третьей строки общий коэффициент «-1/7».
Теперь все красиво. Дело за малым — записать матрицу опять в виде системы уравнений и вычислить корни
x + 2y + 4z = 12 (1)
Тот алгоритм, по которому сейчас будут находиться корни, называется обратным ходом в методе Гаусса. В уравнении (3) содержится значение z:
Далее возвращаемся ко второму уравнению:
y = (24 — 11×(61/9))/7 = -65/9
И первое уравнение позволяет найти x:
x = (12 — 4z — 2y)/1 = 12 — 4×(61/9) — 2×(-65/9) = -6/9 = -2/3
Такую систему мы имеем право назвать совместной, да еще и определенной, то есть имеющей единственное решение. Ответ записывается в следующей форме:
Пример неопределенной системы
Вариант решения определенной системы методом Гаусса разобран, теперь необходимо рассмотреть случай, если система неопределенная, то есть для нее можно найти бесконечно много решений.
Сам вид системы уже настораживает, потому что количество неизвестных n = 5, а ранг матрицы системы уже точно меньше этого числа, потому что количество строк m = 4, то есть наибольший порядок определителя-квадрата — 4. Значит, решений существует бесконечное множество, и надо искать его общий вид. Метод Гаусса для линейных уравнений позволяет это сделать.
Сначала, как обычно, составляется расширенная матрица.
Вторая строка: коэффициент k = (-a21/a11) = -3. В третьей строке первый элемент — еще до преобразований, поэтому не надо ничего трогать, надо оставить как есть. Четвертая строка: k = (-а41/а11) = -5
Умножив элементы первой строки на каждый их коэффициентов по очереди и сложив их с нужными строками, получаем матрицу следующего вида:
Как можно видеть, вторая, третья и четвертая строки состоят из элементов, пропорциональных друг другу. Вторая и четвертая вообще одинаковые, поэтому одну из них можно убрать сразу, а оставшуюся умножить на коэффициент «-1» и получить строку номер 3. И опять из двух одинаковых строк оставить одну.
Получилась такая матрица. Пока еще не записана система, нужно здесь определить базисные переменные — стоящие при коэффициентах a11 = 1 и a22 = 1, и свободные — все остальные.
Во втором уравнении есть только одна базисная переменная — x2. Значит, ее можно выразить оттуда, записав через переменные x3, x4, x5, являющиеся свободными.
Подставляем полученное выражение в первое уравнение.
Получилось уравнение, в котором единственная базисная переменная — x1. Проделаем с ней то же, что и с x2.
Все базисные переменные, которых две, выражены через три свободные, теперь можно записывать ответ в общем виде.
Также можно указать одно из частных решений системы. Для таких случаев в качестве значений для свободных переменных выбирают, как правило, нули. Тогда ответом будет:
Пример несовместной системы
Решение несовместных систем уравнений методом Гаусса — самое быстрое. Оно заканчивается сразу же, как только на одном из этапов получается уравнение, не имеющее решения. То есть этап с вычислением корней, достаточно долгий и муторный, отпадает. Рассматривается следующая система:
Как обычно, составляется матрица:
| 1 | 1 | -1 | 0 |
| 2 | -1 | -1 | -2 |
| 4 | 1 | -3 | 5 |
И приводится к ступенчатому виду:
| 1 | 1 | -1 | 0 |
| 0 | -3 | 1 | -2 |
| 0 | 0 | 0 | 7 |
После первого же преобразования в третьей строке содержится уравнение вида
не имеющее решения. Следовательно, система несовместна, и ответом будет пустое множество.
Преимущества и недостатки метода
Если выбирать, каким методом решать СЛАУ на бумаге ручкой, то метод, который был рассмотрен в этой статье, выглядит наиболее привлекательно. В элементарных преобразованиях гораздо труднее запутаться, чем в том случается, если приходится искать вручную определитель или какую-нибудь хитрую обратную матрицу. Однако, если использовать программы для работы с данными такого типа, например, электронные таблицы, то оказывается, что в таких программах уже заложены алгоритмы вычисления основных параметров матриц — определитель, миноры, обратная и транспонированная матрицы и так далее. А если быть уверенным в том, что машина посчитает эти значения сама и не ошибется, целесообразней использовать уже матричный метод или формул Крамера, потому что их применение начинается и заканчивается вычислением определителей и обратными матрицами.
Применение
Поскольку решение методом Гаусса представляет из себя алгоритм, а матрица — это, фактически, двумерный массив, его можно использовать при программировании. Но поскольку статья позиционирует себя, как руководство «для чайников», следует сказать, что самое простое, куда метод можно запихнуть — это электронные таблицы, например, Excel. Опять же, всякие СЛАУ, занесенные в таблицу в виде матрицы, Excel будет рассматривать как двумерный массив. А для операций с ними существует множество приятных команд: сложение (складывать можно только матрицы одинаковых размеров!), умножение на число, перемножение матриц (также с определенными ограничениями), нахождение обратной и транспонированной матриц и, самое главное, вычисление определителя. Если это трудоемкое занятие заменить одной командой, можно гораздо быстрее определять ранг матрицы и, следовательно, устанавливать ее совместность или несовместность.
Метод Гаусса — определение и вычисление с примерами решения
Содержание:
Базисные и свободные переменные:
Пусть задана система
Элементарными преобразованиями системы линейных уравнений называются следующие преобразования:
- исключение из системы уравнения вида
- умножение обеих частей одного из уравнений системы на любое действительное число
;
- перестановка местами уравнений системы;
- прибавление к обеим частям одного из уравнений системы соответствующих частей другого уравнения, умноженных на любое действительное число не равное нулю.
Элементарные преобразования преобразуют данную систему уравнений в эквивалентную систему, т.е. в систему, которая имеет те же решения, что и исходная.
Для решения системы т линейных уравнений с т неизвестными удобно применять метод Гаусса, называемый методом последовательного исключения неизвестных, который основан на применении элементарных преобразований системы. Рассмотрим этот метод.
Предположим, что в системе (6.1.1)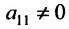
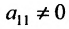
На первом шаге метода Гаусса исключим неизвестное 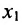
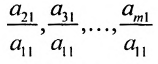
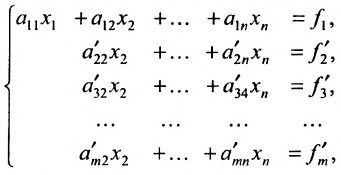
в которой коэффициенты 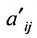
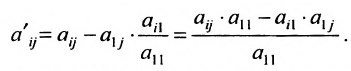
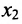
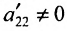
чтобы это условие было выполнено). Для исключения неизвестного 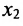
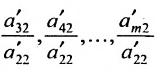
в которой коэффициенты 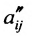
Продолжая аналогичные преобразования, систему (6.1.1) можно привести к одному из видов:
Совокупность элементарных преобразований, приводящих систему (6.1.1) к виду (6.1.4) или (6.1.5) называется прямым ходом метода Гаусса.
Отметим, что если на каком-то шаге прямого хода метода Гаусса получим уравнение вида:
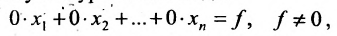
Итак, предположим, что в результате прямого хода метода Гаусса мы получили систему (6.1.4), которая называется системой треугольного вида. Тогда из последнего уравнения находим значение 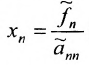
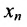
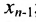
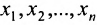
Если же в результате прямого хода метода Гаусса мы получим систему (6.1.5), которая называется системой ступенчатого вида, то из последнего уравнения этой системы находим значение неизвсстного 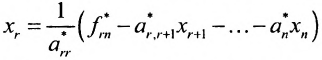
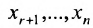
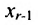
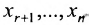
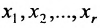
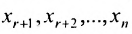
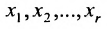
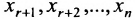
Таким образом, если система (6.1.1) путём элементарных преобразований приводится к треугольному виду (6.1.4), то она имеет единственное решение, если же она приводится к системе ступенчатого вида (6.1.5), то она имеет бесконечное множество решений. При этом неизвестные 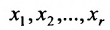
Практически удобнее преобразовывать не саму систему уравнений (6.1.1), а расширенную матрицу системы, соединяя последовательно получающиеся матрицы знаком эквивалентности
Формализовать метод Гаусса можно при помощи следующего алгоритма.
Алгоритм решения системы m линейных уравнений с n неизвестными методом Гаусса
1. Составьте расширенную матрицу коэффициентов системы уравнений так, чтобы 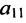
2. Выполните первый шаг метода Гаусса: в первом столбце начиная со второй строки, запишите нули, а все другие элементы вычислите по формуле
Матрица после первого шага примет вид
3. Выполните второй шаг метода Гаусса, предполагая, что 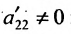
После второго шага матрица примет вид
4. Продолжая аналогичные преобразования, придёте к одному из двух случаев:
а) либо в ходе преобразований получим уравнение вида
тогда данная система несовместна;
б) либо придём к матрице вида:
где 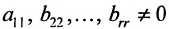
связано с тем, что в процессе преобразований матрицы исключаются строки, состоящие из нулей.
5. Использовав конечную матрицу, составьте систему, при этом возможны два случая:
Система имеет единственное,решение 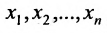
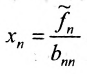
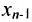
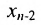
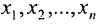
5.2. 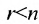
Тогда r неизвестных будут базисными, а остальные (n-r) — свободными. Из последнего уравнения выражаете неизвестное 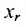
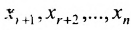
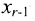
Система имеет в этом случае бесконечное множество решений.
Приведенный алгоритм можно несколько видоизменить и получить алгоритм полного исключения, состоящий в выполнении следующих шагов. На первом шаге:
- составляется расширенная матрица;
- выбирается разрешающий элемент расширенной матрицы
(если
, строки матрицы можно переставить так, чтобы выполнялось условие
);
- элементы разрешающей строки (строки, содержащей разрешающий элемент) оставляем без изменения; элементы разрешающего столбца (столбца, содержащего разрешающий элемент), кроме разрешающего элемента, заменяем нулями;
- все другие элементы вычисляем по правилу прямоугольника: преобразуемый элемент равен разности произведений элементов главной диагонали (главную диагональ образует разрешающий элемент и преобразуемый) и побочной диагонали (побочную диагональ образуют элементы, стоящие в разрешающей строке и разрешающем столбце):
— разрешающий элемент (см. схему).
Последующие шаги выполняем по правилам:
1) выбирается разрешающий элемент 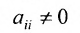
2) элементы разрешающей строки оставляем без изменения;
3) все элементы разрешающего столбца, кроме разрешающего элемента, заменяем нулями; • •
4) все другие элементы матрицы пересчитываем по правилу прямоугольника.
На последнем шаге делим элементы строк на диагональные элементы матрицы, записанные слева от вертикальной черты, и получаем решение системы.
Пример:
Решить систему уравнений:
Решение:
Составим расширенную матрицу системы, и применим алгоритм полного исключения, обозначая разрешающий элемент символом
Из последней матрицы находим следующее решение системы
уравнении:
Ответ:
Пример:
Решить систему уравнений:
Решение:
Составим расширенную матрицу системы, и применим алгоритм полного исключения, обозначая разрешающий элемент символом
Система привелась к ступенчатому виду (трапециевидной форме):
в которой неизвестные 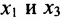
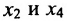
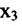
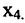
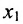
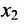
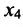
в котором 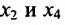
Если в общем решении положить 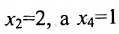
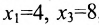
Ответ: система имеет бесконечное множество решений, общее решение которой записывается в виде:
Пример:
Решить систему уравнений:
Решение:
Составим расширенную матрицу системы, и применим алгоритм полного исключения, обозначая разрешающий элемент символом 
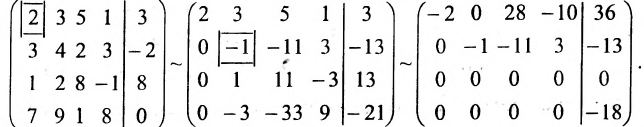
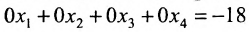
Ответ: система несовместна.
Замечание 1. Если дана система уравнений (6.1.1), в которой число уравнений m равно числу неизвестных n (m=n) и определитель этой системы 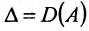
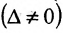
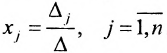
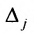
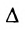
Если же такую систему (m-n) записать в матричной форме AX=F, то её решение можно найти по формуле 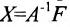
Замечание 2. Используя метод Гаусса, тем самым и алгоритм полного исключения, можно находить обратную матрицу. Для этого составляется расширенная матрица, в которой слева от вертикальной черты записана матрица А, а справа — единичная матрица. Реализовав алгоритм полного исключения, справа от вертикальной черты получаем обратную матрицу, а слева — единичную.
Пример:
Найти обратную матрицу для матрицы:
Решение:
то обратная матрица 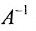
Покажем, что
ответ
Исследование совместности и определённости системы. Теорема Кронекера-Капелли
Рассмотрим систему (6.1.1) m линейных уравнений с n неизвестными при любых m и n (случай m=n не исключается). Вопрос о совместности системы решается следующим критерием.
Теорема 6.2.1. (критерий Кронкера-Капелли). Для того, чтобы система линейных уравнений(6.1.1) была совместна, необходимо и достаточно, чтобы ранг матрицы А системы был равен рангу расширенной матрицы 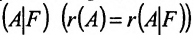
Доказательство и Необходимость:
Предположим, что система (6.1.1) совместна и 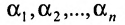
Из этих равенств следует, что последний столбец матрицы 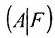
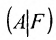
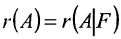
Достаточность. Пусть 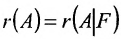
столбцов матрицы А, которые одновременно будут базисными столбцами и матрицы 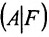
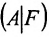
где 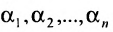
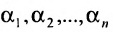
эта система совместна.
Совместная система линейных уравнений (6.1.1) может быть либо определенной, либо неопределенной.
Следующая теорема даст критерий определенности.
Теорема 6.2.2. Совместная система линейных уравнений имеет единственное решение тогда и только тогда, когда ранг матрицы А системы равен числу п ее неизвестных.
Таким образом, если число уравнений m системы (6.1.1) меньше числа ее неизвестных n и система совместна, то ранг матрицы системы 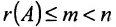
В случае 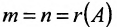
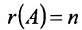
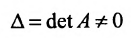
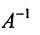
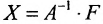
Следует отметить, что, решая систему (6.1.1) методом Гаусса, мы определяем и совместность, и определённость системы.
Пример:
Исследовать на совместность и определённость следующую систему линейных уравнений:
Решение:
Составим расширенную матрицу заданной системы. Определяя её ранг, находим тем самым и ранг матрицы системы. Для нахождения ранга матрицы применим алгоритм метода Гаусса.
Из последней матрицы следует, что ранг расширенной матрицы 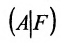
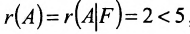
Однородные системы линейных уравнений
Система линейных уравнений (6.1.1) называется однородной, если все свободные члены 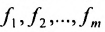
Эта система всегда совместна, так как очевидно, что она имеет нулевое решение
Для однородной системы важно установить, имеет ли она ненулевые решения. Этот факт устанавливается следующей теоремой.
Теорема 6.3.1. Для того, чтобы однородная система имела ненулевые решения, необходимо и достаточно, чтобы ранг г матрицы А системы был меньше числа неизвестных n (r
Доказательство. Необходимость. Пусть система (6.3.1) имеет ненулевое решение. Тогда она неопределённая, т.к. имеет еще и нулевое решение. В силу теоремы 6.2.2 ранг матрицы неопределённой системы не может равняться n потому что при r(А)=n система определённая. Следовательно, 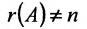
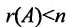
Достаточность. Если 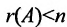
Следствие 1. Если число неизвестных в однородной системе больше числа уравнений, то однородная система имеет ненулевые решения.
Доказательство. Действительно, ранг матрицы системы (6.3.1) не может превышать m. Но так как по условию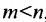
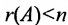
Следствие 2. Для того, чтобы однородная система с квадрат-ной матрицей имела ненулевые решения, необходимо и достаточно, чтобы её определитель 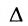
Доказательство. Рассмотрим однородную систему с квадратной матрицей:
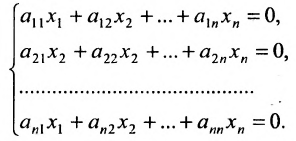
Если определитель матрицы системы 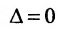
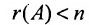
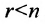
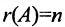
Пример:
Решить систему однородных линейных уравнений:
Решение:
Составим матицу системы и применим алгоритм полного исключения:
Из последней матрицы следует, что 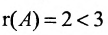
Используя последнюю матрицу, последовательно находим общее решение:
Неизвестные 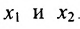
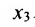
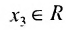
Фундаментальная система решений. Общее решение неоднородной системы линейных уравнений
Рассмотрим систему однородных линейных уравнений
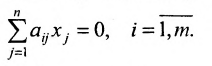
системы m линейных однородных уравнений с n неизвестными можно рассматривать как вектор-строку 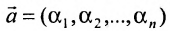
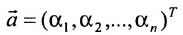
1) сумма двух решений также является решением системы, т.е.
если 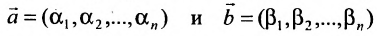
(6.4.1), то и 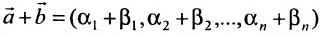
2) произведение решений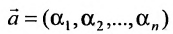
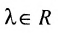
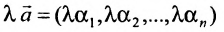
Из приведенных свойств следует, что
3) линейная комбинация решений системы (6.4.1) является решением этой системы.
В частности, если однородная система (6.4.1) имеет хотя бы одно ненулевое решение, то из него умножением на произвольные числа, можно получить бесконечное множество решений.
Определение 6.4.1. Фундаментальной системой решений для системы однородных линейных уравнений (6.4.1) называется линейно независимая система решений, через которую линейно выражается любое решение системы (6.4.1).
Заметим, что если ранг матрицы системы (6.4.1) равен числу неизвестных n (r(А)=n), то эта система не имеет фундаментальной системы решений, так как единственным решением будет нулевое решение, составляющее линейно зависимую систему. Существование и число фундаментальных решений определяется следующей теоремой.
Теорема 6.4.1. Если ранг матрицы однородной системы уравнений (6.4.1) меньше числа неизвестных (r(А)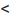
Сформулируем алгоритм построения фундаментальной системы решений:
- Выбираем любой определитель
порядка n-r, отличный от нуля, в частности, определитель порядка n-r, у которого элементы главной диагонали равны единице, а остальные — нули.
- Свободным неизвестным придаём поочерёдно значения, равные элементам первой, второй и т.д. строк определителя
, и каждый раз из общего решения находим соответствующие значения базисных неизвестных.
- Из полученных n-r решений составляют фундаментальную систему решений.
Меняя произвольно определитель 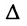
Пример:
Найти общее решение и фундаментальную систему решений для однородной системы уравнений:
Решение:
Составим матрицу системы и применим алгоритм полного исключения.
Для последней матрицы составляем систему:
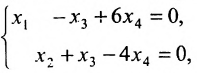
, из которой находим общее решение:
в котором 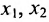
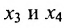
Построим фундаментальную систему решений. Для этого выбираем определитель 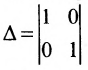
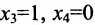
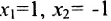
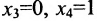
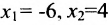
Таким образом, построенные два решения (1; -1; 1; 0) и (-6; 4; 0; 1) составляют фундаментальную систему решений.
Если ранг матрицы системы однородных линейных уравнений (6.4.1) на единицу меньше числа неизвестных: 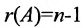
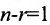
Рассмотрим теперь неоднородную систему m линейных уравнений с n неизвестными (6.1.1). Если в системе (6.1.1) положить 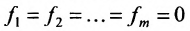
Решения системы (6.1.1) и её приведенной системы удовлетворяют свойствам:
- Сумма и разность любого решения системы (6.1.1) и любого решения её приведенной системы является решением неоднородной системы.
- Все решения неоднородной системы можно получить, прибавляя к одному (любому) её решению поочерёдно все решения её приведенной системы.
Из этих свойств следует теорема.
Теорема 6.4.2. Общее решение неоднородной системы (6.1.1.) определяется суммой любого частного решения этой системы и общего решения её приведенной системы.
Пример:
Найти общее решение системы:
Решение:
Составим расширенную матрицу (A|F) заданной системы и применим алгоритм полного исключения:
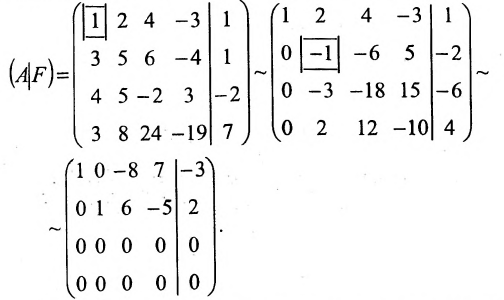
Преобразованной матрице соответствует система уравнений:
из которой находим общее решение системы:
, где 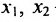
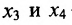
Покажем, что это общее решение определяется суммой любого частного решения заданной системы и общего решения приведенной системы.
Подставляя вместо свободных неизвестных 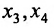
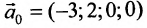
Очевидно, что общее решение приведенной системы имеет вид:
Суммируя частное решение заданной системы и общее решение приведенной системы, получим общее решение (6.4.2) исходной системы.
Отметим, что общее решение системы (6.1.1) можно представить в векторном виде:
где 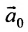
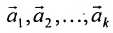
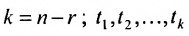
Формула (6.4.4) называется общим решением системы (6.1.1) в векторной форме.
Запишем общее решение системы примера 6.4.1 в векторной форме. Для этого определим фундаментальную систему решений приведенной системы. Возьмём определитель 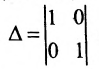
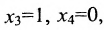
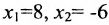
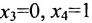
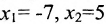
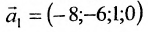
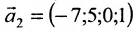
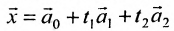
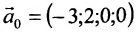
Определение метода Гаусса
Исторически первым, наиболее распространенным методом решения систем линейных уравнений является метод Гаусса, или метод последовательного исключения неизвестных. Сущность этого метода состоит в том, что посредством последовательных исключений неизвестных данная система превращается в ступенчатую (в частности, треугольную) систему, равносильную данной. При практическом решении системы линейных уравнений методом Гаусса удобнее приводить к ступенчатому виду не саму систему уравнений, а расширенную матрицу этой системы, выполняя элементарные преобразования над ее строками. Последовательно получающиеся в ходе преобразования матрицы обычно соединяют знаком эквивалентности.
Пример:
Решить систему уравнений методом Гаусса:
Решение:
Выпишем расширенную матрицу данной системы 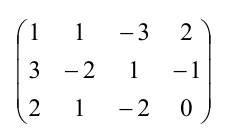
а) из ее второй и третьей строк вычтем первую, умноженную соответственно на 3 и 2:
б) третью строку умножим на (-5) и прибавим к ней вторую:
В результате всех этих преобразований данная система приводится к треугольному виду:
Из последнего уравнения находим 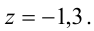
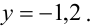
Вычисление метода Гаусса
Этот метод основан на следующей теореме.
Теорема:
Элементарные преобразования не изменяют ранга матрицы.
К элементарным преобразованиям матрицы относят:
- перестановку двух параллельных рядов;
- умножение какого-нибудь ряда на число, отличное от нуля;
- прибавление к какому-либо ряду матрицы другого, параллельного ему ряда, умноженного на произвольное число.
Путем элементарных преобразований исходную матрицу можно привести к трапециевидной форме
где все диагональные элементы 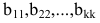
Пример:
Найти ранг матрицы
1) методом окаймляющих миноров;
2 ) методом Гаусса.
Указать один из базисных миноров.
Решение:
1. Найдем ранг матрицы методом окаймляющих миноров. Выберем минор второго порядка, отличный от нуля. Например,
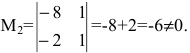
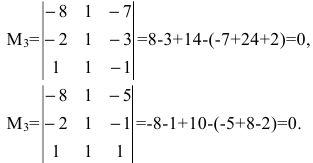
2. Найдем ранг матрицы методом Гаусса. Производя последовательно элементарные преобразования, получим:
- переставили первую и третью строки;
- первую строку умножили на 2 и прибавили ко второй, первую строку умножили на 8 и прибавили к третьей;
- вторую строку умножили на -3 и прибавили к третьей.
Последняя матрица имеет трапециевидную форму и ее ранг равен двум. Следовательно, ранг исходной матрицы также равен двум.
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Прямая линия на плоскости и в пространстве
- Плоскость в трехмерном пространстве
- Функция одной переменной
- Производная функции одной переменной
- Дифференциальные уравнения с примерами
- Обратная матрица — определение и нахождение
- Ранг матрицы — определение и вычисление
- Определители второго и третьего порядков и их свойства
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Telegram и логотип telegram являются товарными знаками корпорации Telegram FZ-LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.


















































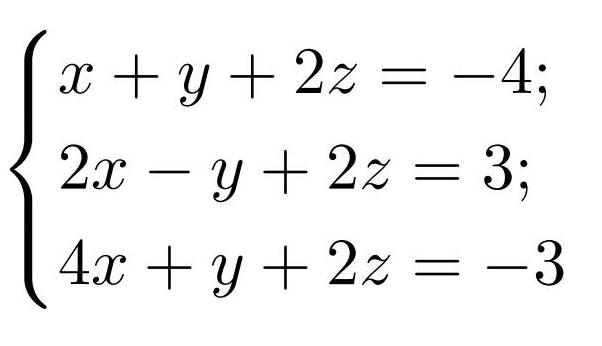
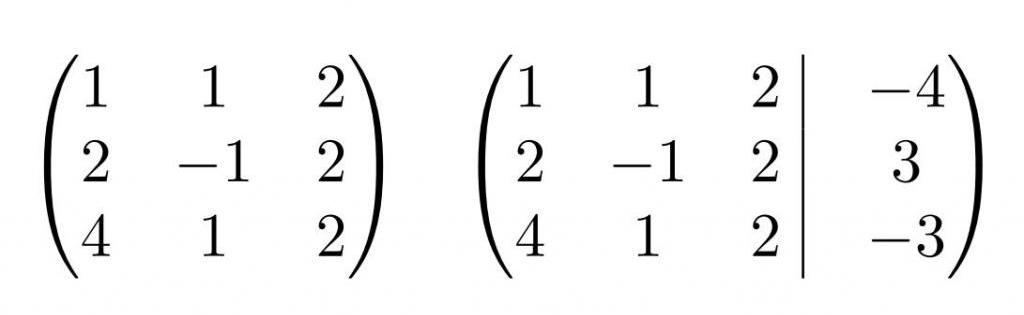
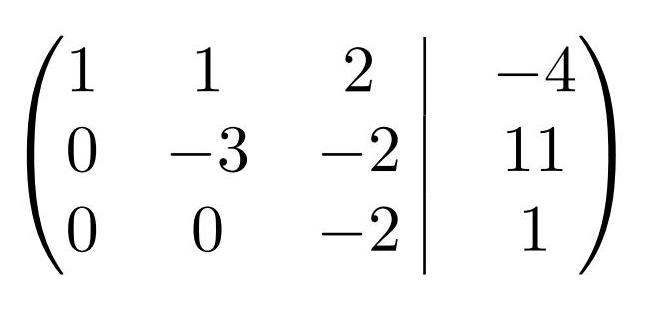


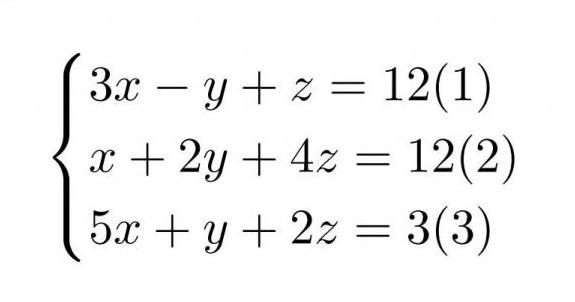

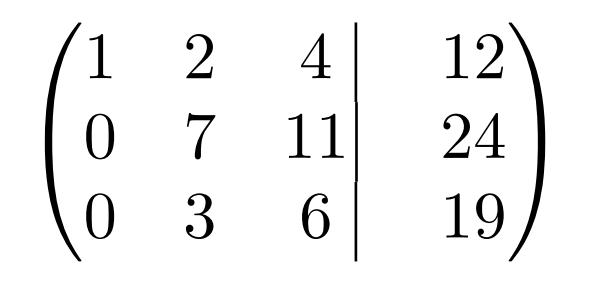
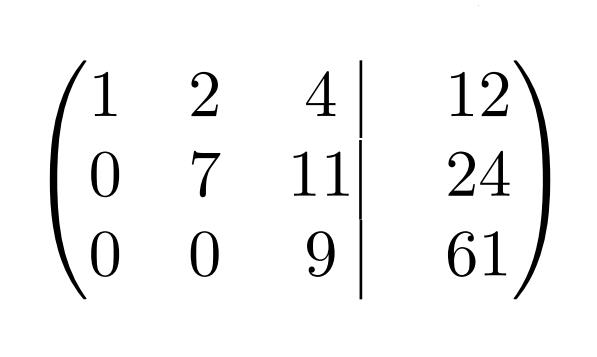
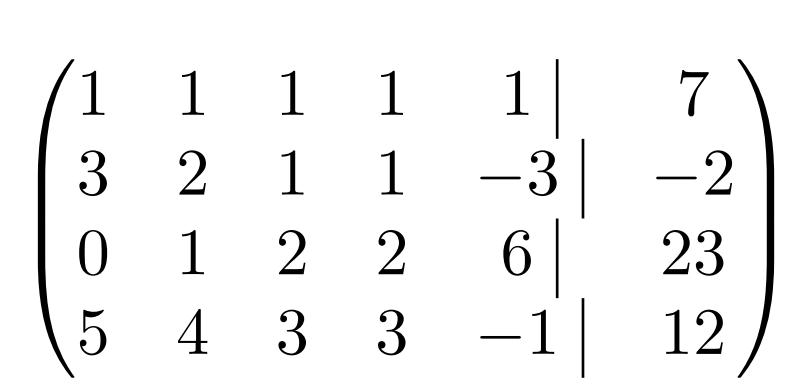
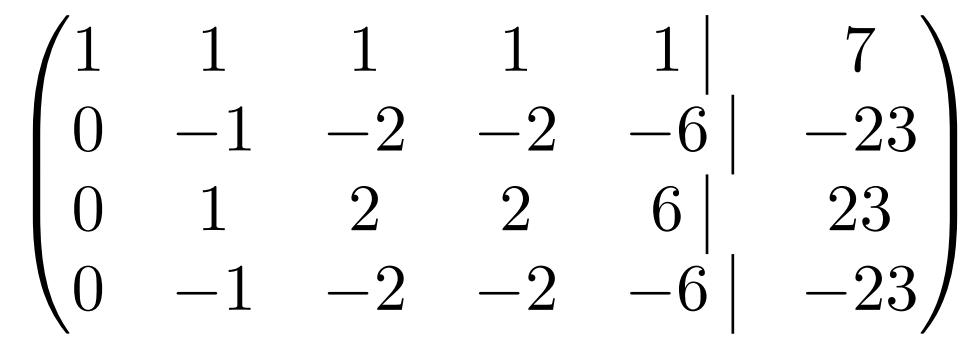
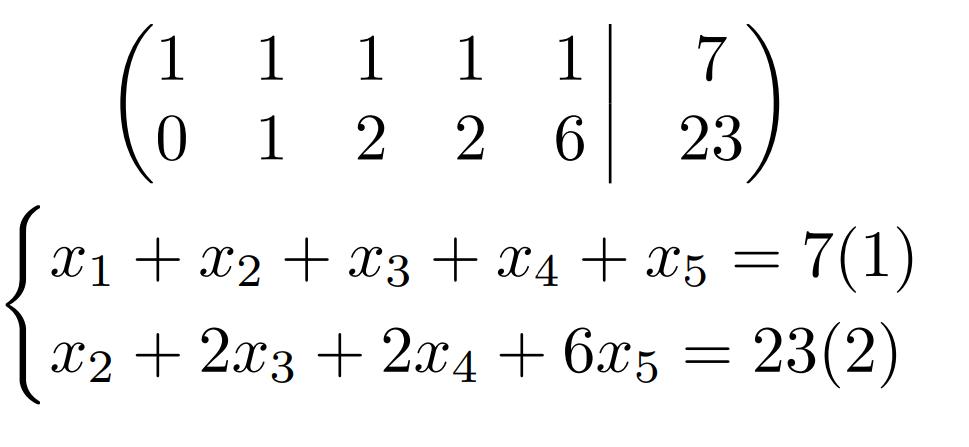

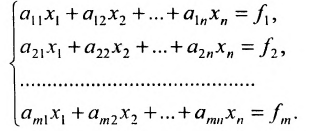
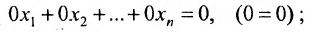
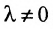 ;
;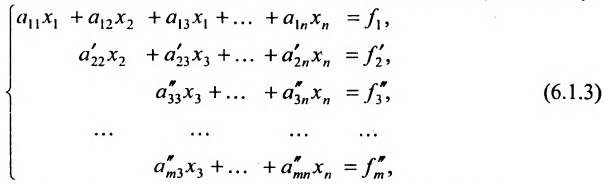
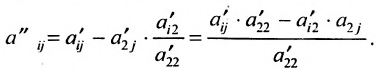
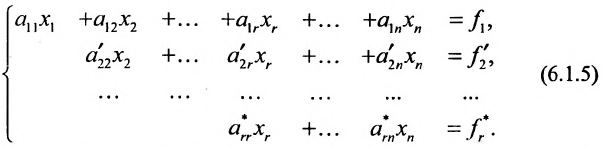

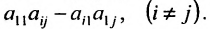
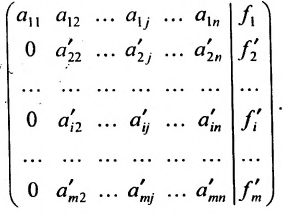
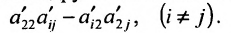

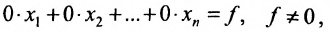
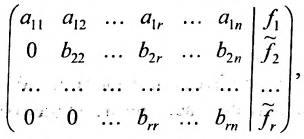
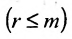
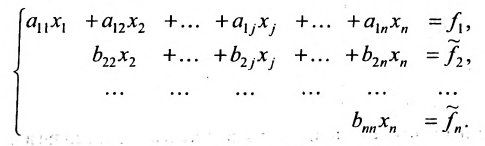
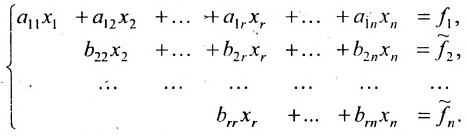
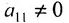 (если
(если 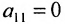 , строки матрицы можно переставить так, чтобы выполнялось условие
, строки матрицы можно переставить так, чтобы выполнялось условие 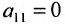 );
);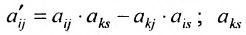 — разрешающий элемент (см. схему).
— разрешающий элемент (см. схему).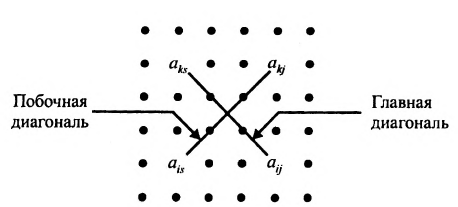
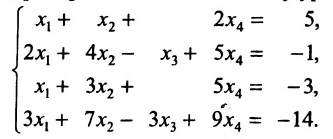


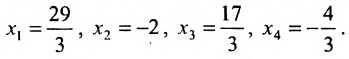
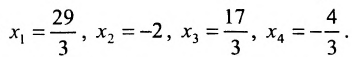
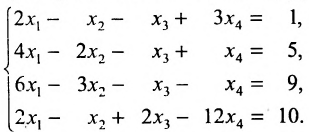

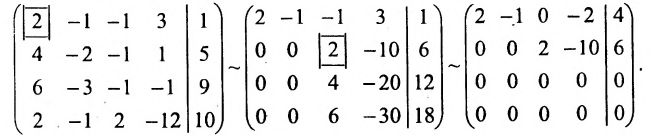

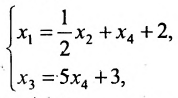
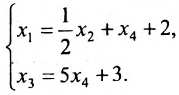
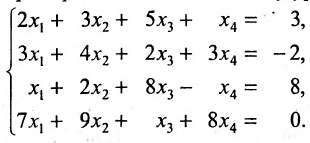
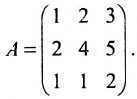
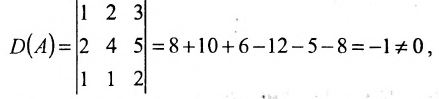

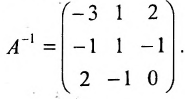
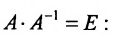
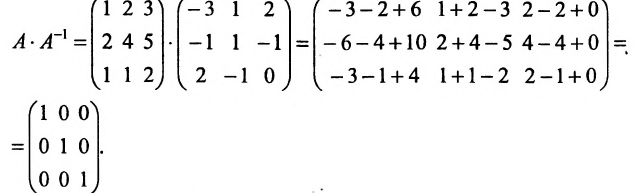
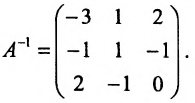
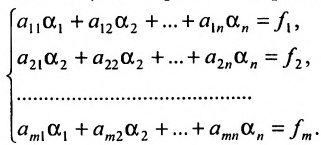
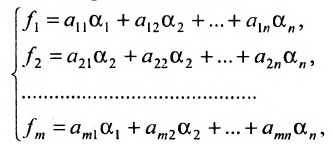
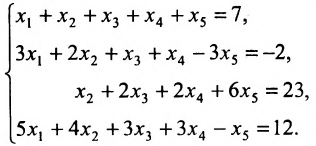

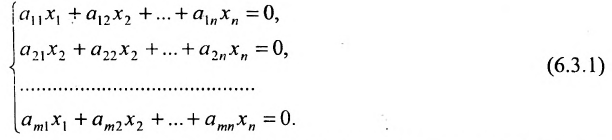
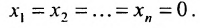
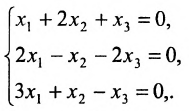
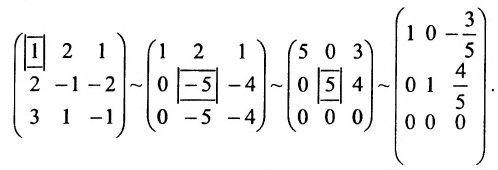
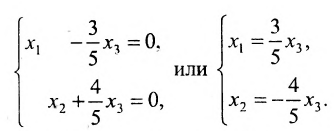
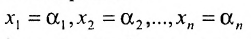
 порядка n-r, отличный от нуля, в частности, определитель порядка n-r, у которого элементы главной диагонали равны единице, а остальные — нули.
порядка n-r, отличный от нуля, в частности, определитель порядка n-r, у которого элементы главной диагонали равны единице, а остальные — нули. , и каждый раз из общего решения находим соответствующие значения базисных неизвестных.
, и каждый раз из общего решения находим соответствующие значения базисных неизвестных.