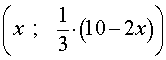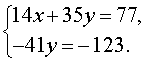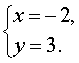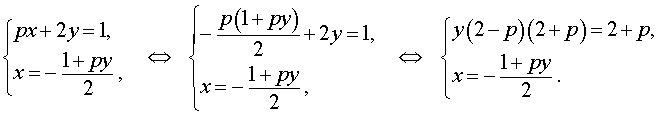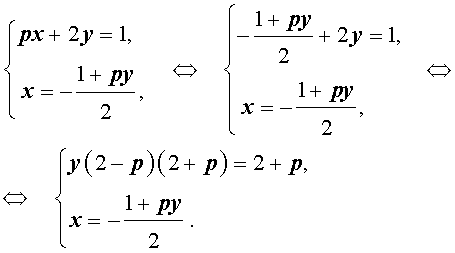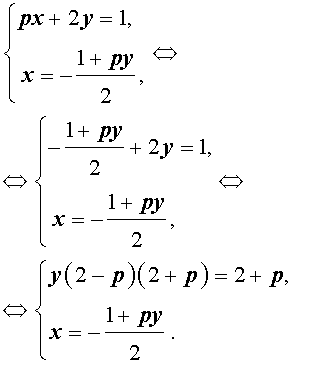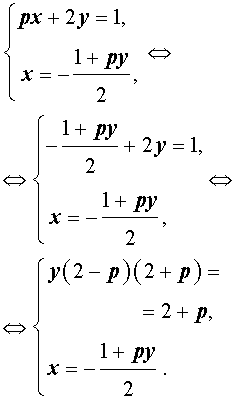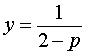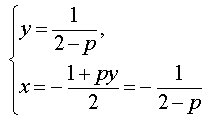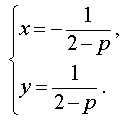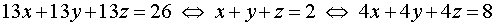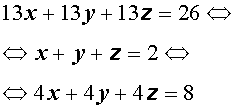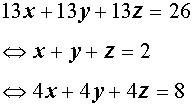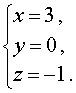Линейные уравнения (уравнения первой степени) с двумя неизвестными Линейные уравнения (уравнения первой степени) с двумя неизвестными |
 Системы из двух линейных уравнений с двумя неизвестными Системы из двух линейных уравнений с двумя неизвестными |
 Системы из трех линейных уравнений с тремя неизвестными Системы из трех линейных уравнений с тремя неизвестными |
- Линейные уравнения (уравнения первой степени) с двумя неизвестными
- Системы из двух линейных уравнений с двумя неизвестными
- Системы из трех линейных уравнений с тремя неизвестными
- Уравнения первой степени: формулы, как их решать, пример, упражнения
- Содержание:
- Как решать уравнения первой степени
- Графическая интерпретация
- Примеры простых линейных уравнений
- Целочисленные уравнения
- Дробные уравнения
- Буквальные уравнения
- Системы уравнений первой степени
- Линейные уравнения с абсолютным значением
- Простые решаемые упражнения
- — Упражнение 1
- Решение
- — Упражнение 2.
- Решение
- — Упражнение 3.
- Решение
- Ссылки
- Алгебра. 7 класс
Видео:ПОСМОТРИ это видео, если хочешь решить систему линейных уравнений! Метод ПодстановкиСкачать

Линейные уравнения (уравнения первой степени) с двумя неизвестными
Определение 1 . Линейным уравнением (уравнением первой степени) с двумя неизвестными x и y называют уравнение, имеющее вид
| ax +by = c , | (1) |
где a , b , c – заданные числа.
Определение 2 . Решением уравнения (1) называют пару чисел (x ; y) , для которых формула (1) является верным равенством.
Пример 1 . Найти решение уравнения
| 2x +3y = 10 | (2) |
Решение . Выразим из равенства (2) переменную y через переменную x :
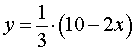 | (3) |
Из формулы (3) следует, что решениями уравнения (2) служат все пары чисел вида
где x – любое число.
Замечание . Как видно из решения примера 1, уравнение (2) имеет бесконечно много решений. Однако важно отметить, что не любая пара чисел (x ; y) является решением этого уравнения. Для того, чтобы получить какое-нибудь решение уравнения (2), число x можно взять любым, а число y после этого вычислить по формуле (3).
Видео:Решение системы линейных уравнений с двумя переменными способом подстановки. 6 класс.Скачать

Системы из двух линейных уравнений с двумя неизвестными
Определение 3 . Системой из двух линейных уравнений с двумя неизвестными x и y называют систему уравнений, имеющую вид
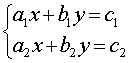 | (4) |
Определение 4 . В системе уравнений (4) числа a1 , b1 , a2 , b2 называют коэффициентами при неизвестных , а числа c1 , c2 – свободными членами .
Определение 5 . Решением системы уравнений (4) называют пару чисел (x ; y) , являющуюся решением как одного, так и другого уравнения системы (4).
Определение 6 . Две системы уравнений называют равносильными (эквивалентными) , если все решения первой системы уравнений являются решениями второй системы, и все решения второй системы являются решениями первой системы.
Равносильность систем уравнений обозначают, используя символ «
Системы линейных уравнений решают с помощью метода последовательного исключения неизвестных , который мы проиллюстрируем на примерах.
Пример 2 . Решить систему уравнений
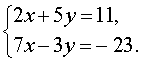 | (5) |
Решение . Для того, чтобы решить систему (5) исключим из второго уравнения системы неизвестное х .
С этой целью сначала преобразуем систему (5) к виду, в котором коэффициенты при неизвестном x в первом и втором уравнениях системы станут одинаковыми.
Если первое уравнение системы (5) умножить на коэффициент, стоящий при x во втором уравнении (число 7 ), а второе уравнение умножить на коэффициент, стоящий при x в первом уравнении (число 2 ), то система (5) примет вид
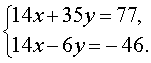 | (6) |
Теперь совершим над системой (6) следующие преобразования:
- первое уравнение системы оставим без изменений;
- из второго уравнения вычтем первое уравнение и заменим второе уравнение системы на полученную разность.
В результате система (6) преобразуется в равносильную ей систему
Из второго уравнения находим y = 3 , и, подставив это значение в первое уравнение, получаем
Пример 3 . Найти все значения параметра p , при которых система уравнений
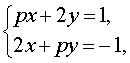 | (7) |
а) имеет единственное решение;
б) имеет бесконечно много решений;
в) не имеет решений.
Решение . Выражая x через y из второго уравнения системы (7) и подставляя полученное выражение вместо x в первое уравнение системы (7), получим
Следовательно, система (7) равносильна системе
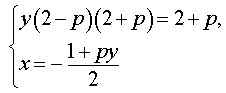 | (8) |
Исследуем решения системы (8) в зависимости от значений параметра p . Для этого сначала рассмотрим первое уравнение системы (8):
| y (2 – p) (2 + p) = 2 + p | (9) |
Если 
Следовательно, система (8) равносильна системе
Таким образом, в случае, когда 
Если p = – 2 , то уравнение (9) принимает вид
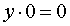
и его решением является любое число 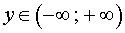
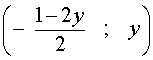
где y – любое число.
Если p = 2 , то уравнение (9) принимает вид
и решений не имеет, откуда вытекает, что и система (7) решений не имеет.
Видео:Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

Системы из трех линейных уравнений с тремя неизвестными
Определение 7 . Системой из трех линейных уравнений с тремя неизвестными x , y и z называют систему уравнений, имеющую вид
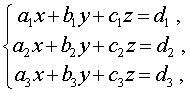 | (10) |
Определение 9 . Решением системы уравнений (10) называют тройку чисел (x ; y ; z) , при подстановке которых в каждое из трех уравнений системы (10) получается верное равенство.
Пример 4 . Решить систему уравнений
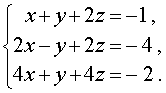 | (11) |
Решение . Будем решать систему (11) при помощи метода последовательного исключения неизвестных .
Для этого сначала исключим из второго и третьего уравнений системы неизвестное y , совершив над системой (11) следующие преобразования:
- первое уравнение системы оставим без изменений;
- ко второму уравнению прибавим первое уравнение и заменим второе уравнение системы на полученную сумму;
- из третьего уравнения вычтем первое уравнение и заменим третье уравнение системы на полученную разность.
В результате система (11) преобразуется в равносильную ей систему
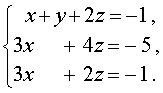 | (12) |
Теперь исключим из третьего уравнения системы неизвестное x , совершив над системой (12) следующие преобразования:
- первое и второе уравнения системы оставим без изменений;
- из третьего уравнения вычтем второе уравнение и заменим третье уравнение системы на полученную разность.
В результате система (12) преобразуется в равносильную ей систему
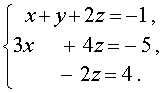 | (13) |
Из системы (13) последовательно находим
Пример 5 . Решить систему уравнений
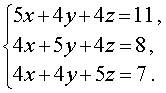 | (14) |
Решение . Заметим, что из данной системы можно получить удобное следствие, сложив все три уравнения системы:
Если числа (x ; y ; z) являются решением системы (14), то они должны удовлетворять и уравнению (15). Однако в таком случае числа (x ; y ; z) должны также быть решением системы, которая получается, если из каждого уравнения системы (14) вычесть уравнение (15):
Поскольку мы использовали следствие из системы (14), не задумываясь о том, являются ли сделанные преобразования системы (14) равносильными, то полученный результат нужно проверить. Подставив тройку чисел (3 ; 0 ; –1) в исходную систему (14), убеждаемся, что числа (3 ; 0 ; –1) действительно являются ее решением.
Замечание . Рекомендуем посетителю нашего сайта, интересующемуся методами решения систем уравнений, ознакомиться также c разделом справочника «Системы с нелинейными уравнениями» и нашим учебным пособием «Системы уравнений».
Видео:Решение систем уравнений второго порядка. 8 класс.Скачать

Уравнения первой степени: формулы, как их решать, пример, упражнения
Уравнения первой степени: формулы, как их решать, пример, упражнения — Наука
Видео:ЛИНЕЙНЫЕ УРАВНЕНИЯ - Как решать линейные уравнения // Подготовка к ЕГЭ по МатематикеСкачать

Содержание:
В первая степень или линейные уравнения с неизвестным — это те, которые могут быть выражены как сумма двух членов следующим образом:
куда а и б, с участием к ≠ 0, являются действительными числами R или также комплексными C. Чтобы решить эту задачу, члены транспонируются, что означает изменение членов с одной стороны равенства на другую.
Чтобы решить неизвестное, транспонируется член + b, который должен перейти в правую часть равенства с измененным знаком.
Затем значение x очищается следующим образом:
В качестве примера мы собираемся решить следующее уравнение:
Переносим член -5 в правую часть с измененным знаком:
Это эквивалентно добавлению 5 к обеим сторонам исходного уравнения:
6x — 5 + 5 = 4 + 5 → 6x = 9
А теперь решаем неизвестный «х»:
Это эквивалентно делению обеих частей равенства на 6. Таким образом, мы можем использовать следующее, чтобы получить решение:
-Вы можете прибавить или вычесть одно и то же количество к обеим сторонам равенства в уравнении, не изменяя его.
-Вы также можете умножить (или разделить) на одинаковую величину все члены как слева, так и справа от уравнения.
-И если оба члена уравнения возведены в одну и ту же степень, равенство также не изменяется.
Видео:Решение систем уравнений методом подстановкиСкачать

Как решать уравнения первой степени
Решение уравнения первой степени также называется его корнем. Именно значение x преобразует исходное выражение в равенство. Например в:
Если мы подставим в это уравнение x = 5, мы получим:
Поскольку линейные уравнения первой степени бывают разных форм, которые иногда не очевидны, существует ряд общих правил, которые включают в себя несколько алгебраических манипуляций, чтобы найти значение неизвестного:
— Во-первых, если есть указанные операции, их необходимо провести.
— Группирующие символы, такие как круглые скобки, скобки и фигурные скобки, если они существуют, должны быть удалены с сохранением соответствующих знаков.
— Термины переносятся так, что все те, которые содержат неизвестное, помещаются с одной стороны равенства, а те, которые не содержат его, с другой.
-Затем все подобные термины сокращаются до формы топор = -b.
–И последний шаг — прояснить неизвестное.
Видео:Алгебра 7 класс (Урок№46 - Системы двух уравнений первой степени с двумя неизвестными.)Скачать

Графическая интерпретация
Уравнение первой степени, поставленное в начале, может быть получено из уравнения прямой y = mx + c, в результате чего y = 0. Полученное значение x соответствует пересечению прямой с горизонтальной осью.
На следующем рисунке есть три линии. Начиная с зеленой линии, уравнение которой:
Делая y = 0 в уравнении прямой, получается уравнение первой степени:
Чье решение — x = 6/2 = 3. Теперь, когда мы детализируем график, легко понять, что на самом деле линия пересекает горизонтальную ось в точке x = 3.
Синяя линия пересекает ось x в точке x = 5, которая является решением уравнения –x + 5 = 0. Наконец, линия с уравнением y = 0,5x + 2 пересекает ось x в точке x = — 4, что легко увидеть из уравнения первой степени:
Видео:Решение системы линейных уравнений графическим методом. 7 класс.Скачать

Примеры простых линейных уравнений
Видео:Решение систем уравнений методом сложенияСкачать

Целочисленные уравнения
Это те, в терминах которых нет знаменателей, например:
Видео:Система уравнений. Метод алгебраического сложенияСкачать

Дробные уравнения
Эти уравнения содержат по крайней мере один знаменатель, отличный от 1. Чтобы решить их, рекомендуется умножить все члены на наименьшее общее кратное (НОК) знаменателей, чтобы исключить их.
Следующее уравнение является дробным типом:
Поскольку эти числа малы, нетрудно увидеть, что m.c.m (6, 8,12) = 24. Этот результат легко получить, выразив числа как произведение простых чисел или их степеней, давайте посмотрим:
Наименьшее общее кратное определяется путем умножения общего и необычного множителей 6, 8 и 12 на их наибольшую экспоненту, затем:
lcm (6,8,12) = 2 3 ⋅3 = 8 × 3 = 24
Поскольку у нас есть наименьшее общее кратное, его нужно умножить на каждый из членов уравнения:
4 (x + 5) -3 (2x + 3) = 2 (1-5x)
Мы пользуемся распределительным свойством:
4x + 20 — 6x -9 = 2 — 10x
Все члены, содержащие неизвестный «x», сгруппированы в левой части равенства, а независимые или числовые члены остаются в правой части:
4x — 6x + 10 x = 2 +9 — 20
Видео:Решение системы линейных неравенств с одной переменной. 6 класс.Скачать
Буквальные уравнения
Это линейные уравнения с одним неизвестным, которые, однако, сопровождаются буквальными коэффициентами (буквами). Эти буквы обрабатываются так же, как и числа. Пример буквального уравнения первой степени:
Это уравнение решается так же, как если бы независимые члены и коэффициенты были числовыми:
-3ax — 5x = — b — 2a
Факторизация неизвестного «x»:
х (-3a — 5) = — b — 2a
х = (- b — 2a) / (-3a — 5) → x = (2a + b) / (3a + 5)
Видео:Алгебра 7 класс (Урок№45 - Уравнения первой степени с двумя неизвестными.)Скачать

Системы уравнений первой степени
Системы уравнений состоят из системы уравнений с двумя или более неизвестными. Решение системы состоит из значений, которые одновременно удовлетворяют уравнениям, и для его однозначного определения должно быть уравнение для каждой неизвестной.
Общий вид системы м линейные уравнения с п неизвестные это:
Если у системы есть решение, оно называется совместимый определен, когда существует бесконечный набор значений, которые удовлетворяют, это неопределенный совместимый, и, наконец, если у нее нет решения, то она несовместимый.
При решении систем линейных уравнений используются несколько методов: редукция, подстановка, выравнивание, графические методы, метод исключения Гаусса-Жордана и использование определителей являются одними из наиболее часто используемых. Но есть и другие алгоритмы решения, более удобные для систем со многими уравнениями и неизвестными.
Пример системы линейных уравнений с двумя неизвестными:
8x — 5 = 7лет — 9
6х = 3у + 6
Решение этой системы представлено далее в разделе решенных упражнений.
Видео:Линейное уравнение с одной переменной. 6 класс.Скачать

Линейные уравнения с абсолютным значением
Абсолютное значение действительного числа — это расстояние между его положением на числовой прямой и нулем на числовой прямой. Поскольку это расстояние, его значение всегда положительно.
Абсолютное значение числа обозначается полосами по модулю: │x│. Абсолютное значение положительного или отрицательного числа всегда положительно, например:
В уравнении абсолютного значения неизвестное находится между стержнями модуля. Рассмотрим следующее простое уравнение:
Есть две возможности, первая — это положительное число x, и в этом случае мы имеем:
Другая возможность состоит в том, что x — отрицательное число, в этом случае:
Это решения этого уравнения. Теперь посмотрим на другой пример:
Сумма внутри столбцов может быть положительной, поэтому:
Или это может быть отрицательно. В таком случае:
-x — 6 = 11 ⇒ -x = 11 + 6 = 17
А ценность неизвестного:
Таким образом, это уравнение абсолютного значения имеет два решения: x1 = 5 и x2 = -17. Мы можем проверить, что оба решения приводят к равенству в исходном уравнении:
Видео:Линейное уравнение с двумя переменными. 7 класс.Скачать

Простые решаемые упражнения
Видео:Система с тремя переменнымиСкачать

— Упражнение 1
Решите следующую систему линейных уравнений с двумя неизвестными:
8x — 5 = 7y -9
6х = 3у + 6
Видео:Решение систем уравнений второй степени. Алгебра, 9 классСкачать

Решение
Как предлагается, эта система идеальна для использования метода подстановки, поскольку во втором уравнении неизвестная Икс практически готов к оформлению:
И его можно сразу подставить в первое уравнение, которое затем становится уравнением первой степени с неизвестным «y»:
8 [(3y + 6) / 6] — 5 = 7y — 9
Знаменатель можно опустить, умножив каждый член на 6:
6. 8⋅ [(3y + 6) / 6] — 6.5 = 6 .7y– 6. 9
8⋅ (3лет + 6) — 30 = 42лет — 54
Применяя распределительное свойство в первом члене справа от равенства:
24 года + 48-30 = 42 года — 54 ⇒ 24 года + 18 = 42 года — 54
Уравнение можно упростить, так как все коэффициенты кратны 6:
4лет + 3 = 7лет — 9
С этим результатом переходим к очистке от x:
х = (3у +6) / 6 → х = (12 + 6) / 6 = 3
Видео:Алгебра.7 класс (Урок№42 - Уравнения первой степени с одним неизвестным.)Скачать

— Упражнение 2.
Решите следующее уравнение:
Видео:Урок по теме СПОСОБ ПОДСТАНОВКИ 7 классСкачать

Решение
Продукты представлены в этом уравнении, и, следуя инструкциям, данным в начале, они должны быть разработаны в первую очередь:
3х — 10х +14 = 5х + 36х + 12
Тогда все члены, содержащие неизвестные, переносятся в левую часть равенства, а в правую часть будут стоять независимые члены:
3x — 10x — 5x — 36x = 12 — 14
Видео:Математика | Система уравнений на желтую звездочку (feat Золотой Медалист по бегу)Скачать

— Упражнение 3.
Сложение трех внутренних углов треугольника дает 180 °. Наивысшее превосходит второстепенное на 35 °, а последнее, в свою очередь, превышает разницу между наибольшим и средним на 20 °. Какие углы?
Решение
Мы будем называть «x» большим углом, «y» — средним, а «z» — наименьшим. Когда в утверждении говорится, что их сумма равна 180º, можно записать:
Тогда мы знаем, что большее превышает меньшее на 35º, мы можем записать это так:
Наконец, наименьшее значение превышает разницу между наибольшим и средним на 20 °:
У нас есть система из 3-х уравнений и 3-х неизвестных:
Решая для z из первого уравнения, мы имеем:
180 — х — у = х — у + 20
Передача неизвестных в левую часть, как всегда:
-x — y — x + y = 20 — 180
Буква «y» отменяется и остается:
Из второго уравнения находим значение z:
z = x — 35 = 80 — 35 = 45º
И значение y находится от первого или третьего:
y = 180 — x — z = 180 — 80 — 45 = 55º
Ссылки
- Балдор. 1977. Элементарная алгебра. Венесуэльские культурные издания.
- Монтерейский институт. Уравнения, неравенства и абсолютное значение. Получено с: montereyinstitute.org.
- Интернет-учитель. Классификация линейных уравнений или уравнений первой степени. Получено с: profesorenlinea.cl.
- Хоффман, Дж. Выбор тем по математике. Том 2.
- Хименес, Р. 2008. Алгебра. Прентис Холл.
- Зилл, Д. 1984. Алгебра и тригонометрия. Макгроу Хилл.
Как мотивировать команду на работе: 8 советов
Алгебра. 7 класс
Конспект урока
Системы двух уравнений первой степени с двумя неизвестными
Перечень рассматриваемых вопросов:
- Линейные уравнения.
- Корень уравнения;
- Решение линейных уравнений.
Уравнение – это равенство, включающее в себя переменную, значение которой нужно вычислить.
Корень уравнения – это число, при подстановке которого в уравнение получается верное равенство.
Переменная – символ, используемый для представления величины, которая может принимать любое из ряда значений.
Свободный член – член уравнения, не содержащий неизвестного.
Решить уравнение – значит найти все его корни или установить, что их нет.
Преобразование – это действия, выполняемые с целью замены исходного выражения на выражение, которое будет тождественно равным исходному.
Решить систему это значит найти все её решения.
Преобразование – это действия, выполняемые с целью замены исходного выражения на выражение, которое будет тождественно равным исходному.
Решение данной системы всякая пара значений неизвестных, удовлетворяющая обоим уравнениям, образующим систему.
Если отыскиваются общие решения двух или нескольких уравнений, то говорят, что эти уравнения образуют систему.
- Никольский С. М. Алгебра: 7 класс. // Никольский С. М., Потапов М. К., Решетников Н. Н., Шевкин А. В. – М.: Просвещение, 2017. – 287 с.
- Чулков П. В. Алгебра: тематические тесты 7 класс. // Чулков П. В. – М.: Просвещение, 2014 – 95 с.
- Потапов М. К. Алгебра: дидактические материалы 7 класс. // Потапов М. К., Шевкин А. В. – М.: Просвещение, 2017. – 96 с.
- Потапов М. К. Рабочая тетрадь по алгебре 7 класс: к учебнику С. М. Никольского и др. «Алгебра: 7 класс». 1, 2 ч. // Потапов М. К., Шевкин А. В. – М.: Просвещение, 2017. – 160 с.
Теоретический материал для самостоятельного изучения.
Пусть даны 2 уравнения с двумя неизвестными, например: x + 2y = 15 и x + 2y = 7.
Каждое из них имеет бесконечное множество решений. Поставим вопрос: среди всех этих решений не будут ли общие для обоих уравнений?
Такие общие решения могут быть, а могут и не быть. Так, общим решением данных уравнений будет то, что легко проверить подстановкой. (Дальше будет показано, что других общих решений эти уравнения иметь не могут).
Но, уравнения не имеют ни одного общего решения. В самом деле, какие бы значения мы ни подставляли, при любых x и y выражение x + 2y не может одновременно равняться 15 и 7. Поэтому ни одно решение первого уравнения не может быть решением второго и ни одно решение второго уравнения не может быть решением первого.
Если отыскиваются общие решения двух или нескольких уравнений, то говорят, что эти уравнения образуют систему.
Всякая пара значений неизвестных, удовлетворяющая обоим уравнениям, образующим систему, называется решением данной системы.
Решить систему это значит найти все её решения.
Решать системы двух уравнений можно с помощью:
- способа подстановки;
- способа уравнивания коэффициентов.
Способ подстановки состоит в том, что:
1) из одного уравнения мы находим выражение одного из неизвестных, например x, через известные величины и другое неизвестное у;
2) найденное выражение подставляем во второе уравнение, в котором после этой подстановки будет содержаться только одно неизвестное у;
3) решаем полученное уравнение и находим значение у;
4) подставляя найденное значение у в выражение неизвестного x, найденное в начале решения, получаем значение х.
Способ уравнивания коэффициентов:
1) обе части одного уравнения умножаются на некоторый множитель; обе части второго уравнения умножаются на другой множитель. Эти множители подбираются так, чтобы коэффициенты при одном из неизвестных в обоих уравнениях после их умножения на эти множители имели одну, и ту же абсолютную величину;
2) складываем два уравнения или вычитаем их друг из друга, смотря по тому, имеют ли уравненные коэффициенты различные или одинаковые знаки; этим одно из неизвестных исключается;
3) решаем полученное уравнение с одним неизвестным;
4) другое неизвестное можно найти тем же приемом, но обычно, проще всего, подставить найденное значение первого неизвестного в любое из данных уравнений и решить получившееся уравнение с одним неизвестным.
В элементарной математике рассматривают только некоторые простые частные случаи систем уравнений второй или высшей степени. Такова в частности, система
Разбор заданий тренировочного модуля
Решим систему, используя метод уравнивания коэффициентов. В данной системе коэффициенты уже уравнены, потому просто сложим почленно оба уравнения, получаем:
Задание 2. Какие значения переменных удовлетворяют системе уравнений:
Решим данную систему, используя метод уравнивания коэффициентов. В данной системе коэффициенты уже уравнены, потому просто вычтем почленно из первого уравнения второе, получаем: