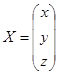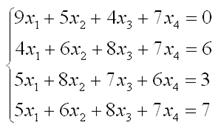Система линейных уравнений методом гаусса в excel

Видео:СЛУ Метод Гаусса в ExcelСкачать

Блог инженера-программиста / шапку скоро поменяю /

Решение системы линейных уравнений методом Гаусса в MS Excel

Автор Инженер

На днях понадобилось найти корни системы линейных уравнений методом Гаусса в Microsoft Excel. Готовый алгоритм решения можно найти в книге Гарнаева «Использование Excel и VBA в экономике и финансах», но объяснение там очень скудное и не совсем понятное. Постараюсь описать подробней для тех, кому может понадобиться этот алгоритм.

Лирическое отступление: в тексте будет предлагаться ввести в диапазон ячеек формулу вида: и т.п., это так-называемые «формулы массива» (формула, выполняющая несколько вычислений над одним или несколькими наборами значений, а затем возвращающая один или несколько результатов. Формулы массива заключены в фигурные скобки ). Microsoft Excel автоматически заключает ее в фигурные скобки ( ). Для введения такого типа формул необходимо выделить весь диапазон, куда нужно вставить формулу, в первой ячейке ввести формулу без фигурных скобок (для примера выше — =A1:B3+$C$2:$C$3 ) и нажать Ctrl+Shift+Enter .

Пускай имеем систему линейных уравнений:

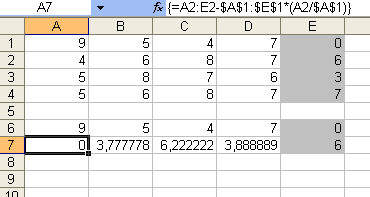
1. Запишем коэффициенты системы уравнений в ячейки A1:D4 а столбец свободных членов в ячейки E1:E4 . Если в ячейке A1 находится 0, необходимо поменять строки местами так, чтоб в этой ячейке было отличное от ноля значение. Для большей наглядности можно добавить заливку ячеек, в которых находятся свободные члены. (скриншот)

2. Необходимо коэффициент при x₁ во всех уравнениях кроме первого привести к 0. Для начала сделаем это для второго уравнения. Скопируем первую строку в ячейки A6:E6 без изменений, в ячейки A7:E7 необходимо ввести формулу: . Таким образом мы от второй строки отнимаем первую, умноженную на A2/$A$1, т.е. отношение первых коэффициентов второго и первого уравнения. Для удобства заполнения строк 8 и 9 ссылки на ячейки первой строки необходимо использовать абсолютные (используем символ $). (скриншот)

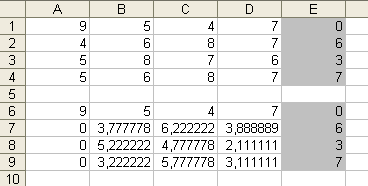
3. Копируем введенную формулу формулу в строки 8 и 9, таким образом избавляемся от коэффициентов перед x₁ во всех уравнениях кроме первого. (скриншот)

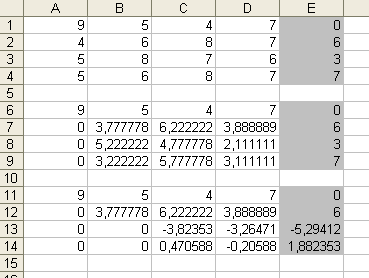
4. Теперь приведем коэффициенты перед x₂ в третьем и четвертом уравнении к 0. Для этого скопируем полученные 6-ю и 7-ю строки (только значения) в строки 11 и 12, а в ячейки A13:E13 введем формулу , которую затем скопируем в ячейки A14:E14 . Таким образом реализуется разность строк 8 и 7, умноженных на коэффициент B8/$B$7 . Не забываем проводить перестановку строк, чтоб избавиться от 0 в знаменателе дроби. (скриншот)

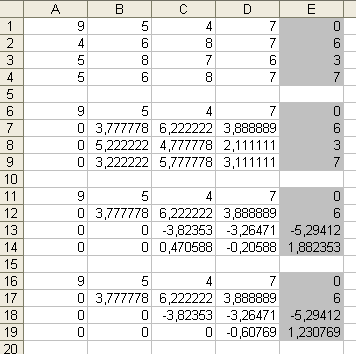
5. Осталось привести коэффициент при x₃ в четвертом уравнении к 0, для этого вновь проделаем аналогичные действия: скопируем полученные 11, 12 и 13-ю строки (только значения) в строки 16-18, а в ячейки A19:E19 введем формулу . Таким образом реализуется разность строк 14 и 13, умноженных на коэффициент C14/$C$13 . Не забываем проводить перестановку строк, чтоб избавиться от 0 в знаменателе дроби. (скриншот)

6. Прямая прогонка методом Гаусса завершена. Обратную прогонку начнем с последней строки полученной матрицы. Необходимо все элементы последней строки разделить на коэффициент при x₄. Для этого в строку 24 введем формулу . (скриншот)

7. Приведем все строки к подобному виду, для этого заполним строки 23, 22, 21 следующими формулами:
23: — отнимаем от третьей строки четвертую умноженную на коэффициент при x₄ третьей строки.
22: — от второй строки отнимаем третью и четвертую, умноженные на соответствующие коэффициенты.
21: — от первой строки отнимаем вторую, третью и четвертую, умноженные на соответствующие коэффициенты.
Результат (корни уравнения) вычислены в ячейках E21:E24 . (скриншот)

UPDATE от 25 апреля 2012 г. Выкладываю xls-файл с решением линейных уравнений методом Гаусса в Microsoft Excel: Показать ссылку

Видео:Решение систем линейных уравнений, урок 4/5. Метод ГауссаСкачать

Решение системы уравнений в Microsoft Excel

Умение решать системы уравнений часто может принести пользу не только в учебе, но и на практике. В то же время, далеко не каждый пользователь ПК знает, что в Экселе существует собственные варианты решений линейных уравнений. Давайте узнаем, как с применением инструментария этого табличного процессора выполнить данную задачу различными способами.

Видео:Решение системы линейных уравнений методом Гаусса в ExcelСкачать

Варианты решений

Любое уравнение может считаться решенным только тогда, когда будут отысканы его корни. В программе Excel существует несколько вариантов поиска корней. Давайте рассмотрим каждый из них.

Способ 1: матричный метод

Самый распространенный способ решения системы линейных уравнений инструментами Excel – это применение матричного метода. Он заключается в построении матрицы из коэффициентов выражений, а затем в создании обратной матрицы. Попробуем использовать данный метод для решения следующей системы уравнений:

Заполняем матрицу числами, которые являются коэффициентами уравнения. Данные числа должны располагаться последовательно по порядку с учетом расположения каждого корня, которому они соответствуют. Если в каком-то выражении один из корней отсутствует, то в этом случае коэффициент считается равным нулю. Если коэффициент не обозначен в уравнении, но соответствующий корень имеется, то считается, что коэффициент равен 1. Обозначаем полученную таблицу, как вектор A.

Отдельно записываем значения после знака «равно». Обозначаем их общим наименованием, как вектор B.

Аргумент «Массив» — это, собственно, адрес исходной таблицы.

Итак, выделяем на листе область пустых ячеек, которая по размеру равна диапазону исходной матрицы. Щелкаем по кнопке «Вставить функцию», расположенную около строки формул.

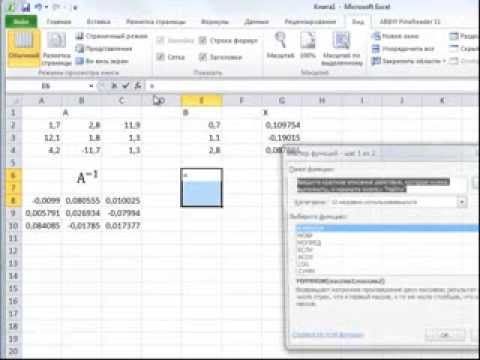
Выполняется запуск Мастера функций. Переходим в категорию «Математические». В представившемся списке ищем наименование «МОБР». После того, как оно отыскано, выделяем его и жмем на кнопку «OK».

Итак, после этого программа производит вычисления и на выходе в предварительно выделенной области мы имеем матрицу, обратную данной.

Теперь нам нужно будет умножить обратную матрицу на матрицу B, которая состоит из одного столбца значений, расположенных после знака «равно» в выражениях. Для умножения таблиц в Экселе также имеется отдельная функция, которая называется МУМНОЖ. Данный оператор имеет следующий синтаксис:

Выделяем диапазон, в нашем случае состоящий из четырех ячеек. Далее опять запускаем Мастер функций, нажав значок «Вставить функцию».

В категории «Математические», запустившегося Мастера функций, выделяем наименование «МУМНОЖ» и жмем на кнопку «OK».

Активируется окно аргументов функции МУМНОЖ. В поле «Массив1» заносим координаты нашей обратной матрицы. Для этого, как и в прошлый раз, устанавливаем курсор в поле и с зажатой левой кнопкой мыши выделяем курсором соответствующую таблицу. Аналогичное действие проводим для внесения координат в поле «Массив2», только на этот раз выделяем значения колонки B. После того, как вышеуказанные действия проведены, опять не спешим жать на кнопку «OK» или клавишу Enter, а набираем комбинацию клавиш Ctrl+Shift+Enter.

Способ 2: подбор параметров

Второй известный способ решения системы уравнений в Экселе – это применение метода подбора параметров. Суть данного метода заключается в поиске от обратного. То есть, основываясь на известном результате, мы производим поиск неизвестного аргумента. Давайте для примера используем квадратное уравнение

Принимаем значение x за равное 0. Высчитываем соответствующее для него значение f(x), применив следующую формулу:

Вместо значения «X» подставляем адрес той ячейки, где расположено число 0, принятое нами за x.

Переходим во вкладку «Данные». Жмем на кнопку «Анализ «что если»». Эта кнопка размещена на ленте в блоке инструментов «Работа с данными». Открывается выпадающий список. Выбираем в нем позицию «Подбор параметра…».

Запускается окно подбора параметров. Как видим, оно состоит из трех полей. В поле «Установить в ячейке» указываем адрес ячейки, в которой находится формула f(x), рассчитанная нами чуть ранее. В поле «Значение» вводим число «0». В поле «Изменяя значения» указываем адрес ячейки, в которой расположено значение x, ранее принятое нами за 0. После выполнения данных действий жмем на кнопку «OK».

После этого Эксель произведет вычисление с помощью подбора параметра. Об этом сообщит появившееся информационное окно. В нем следует нажать на кнопку «OK».

Этот результат также можно проверить, подставив данное значение в решаемое выражение вместо значения x.

Способ 3: метод Крамера

Теперь попробуем решить систему уравнений методом Крамера. Для примера возьмем все ту же систему, которую использовали в Способе 1:

Как и в первом способе, составляем матрицу A из коэффициентов уравнений и таблицу B из значений, которые стоят после знака «равно».

Далее делаем ещё четыре таблицы. Каждая из них является копией матрицы A, только у этих копий поочередно один столбец заменен на таблицу B. У первой таблицы – это первый столбец, у второй таблицы – второй и т.д.

Теперь нам нужно высчитать определители для всех этих таблиц. Система уравнений будет иметь решения только в том случае, если все определители будут иметь значение, отличное от нуля. Для расчета этого значения в Экселе опять имеется отдельная функция – МОПРЕД. Синтаксис данного оператора следующий:

Таким образом, как и у функции МОБР, единственным аргументом выступает ссылка на обрабатываемую таблицу.

Итак, выделяем ячейку, в которой будет выводиться определитель первой матрицы. Затем жмем на знакомую по предыдущим способам кнопку «Вставить функцию».

Активируется окно Мастера функций. Переходим в категорию «Математические» и среди списка операторов выделяем там наименование «МОПРЕД». После этого жмем на кнопку «OK».

Запускается окно аргументов функции МОПРЕД. Как видим, оно имеет только одно поле – «Массив». В это поле вписываем адрес первой преобразованной матрицы. Для этого устанавливаем курсор в поле, а затем выделяем матричный диапазон. После этого жмем на кнопку «OK». Данная функция выводит результат в одну ячейку, а не массивом, поэтому для получения расчета не нужно прибегать к нажатию комбинации клавиш Ctrl+Shift+Enter.

Функция производит подсчет результата и выводит его в заранее выделенную ячейку. Как видим, в нашем случае определитель равен -740, то есть, не является равным нулю, что нам подходит.

Аналогичным образом производим подсчет определителей для остальных трех таблиц.

На завершающем этапе производим подсчет определителя первичной матрицы. Процедура происходит все по тому же алгоритму. Как видим, определитель первичной таблицы тоже отличный от нуля, а значит, матрица считается невырожденной, то есть, система уравнений имеет решения.

Способ 4: метод Гаусса

Решить систему уравнений можно также, применив метод Гаусса. Для примера возьмем более простую систему уравнений из трех неизвестных:

Опять последовательно записываем коэффициенты в таблицу A, а свободные члены, расположенные после знака «равно» — в таблицу B. Но на этот раз сблизим обе таблицы, так как это понадобится нам для работы в дальнейшем. Важным условием является то, чтобы в первой ячейке матрицы A значение было отличным от нуля. В обратном случае следует переставить строки местами.

Копируем первую строку двух соединенных матриц в строчку ниже (для наглядности можно пропустить одну строку). В первую ячейку, которая расположена в строке ещё ниже предыдущей, вводим следующую формулу:

Если вы расположили матрицы по-другому, то и адреса ячеек формулы у вас будут иметь другое значение, но вы сможете высчитать их, сопоставив с теми формулами и изображениями, которые приводятся здесь.

После того, как формула введена, выделите весь ряд ячеек и нажмите комбинацию клавиш Ctrl+Shift+Enter. К ряду будет применена формула массива и он будет заполнен значениями. Таким образом мы произвели вычитание из второй строки первой, умноженной на отношение первых коэффициентов двух первых выражений системы.

После этого копируем полученную строку и вставляем её в строчку ниже.

Выделяем две первые строки после пропущенной строчки. Жмем на кнопку «Копировать», которая расположена на ленте во вкладке «Главная».

Пропускаем строку после последней записи на листе. Выделяем первую ячейку в следующей строке. Кликаем правой кнопкой мыши. В открывшемся контекстном меню наводим курсор на пункт «Специальная вставка». В запустившемся дополнительном списке выбираем позицию «Значения».

В следующую строку вводим формулу массива. В ней производится вычитание из третьей строки предыдущей группы данных второй строки, умноженной на отношение второго коэффициента третьей и второй строки. В нашем случае формула будет иметь следующий вид:

После ввода формулы выделяем весь ряд и применяем сочетание клавиш Ctrl+Shift+Enter.

Теперь следует выполнить обратную прогонку по методу Гаусса. Пропускаем три строки от последней записи. В четвертой строке вводим формулу массива:

Таким образом, мы делим последнюю рассчитанную нами строку на её же третий коэффициент. После того, как набрали формулу, выделяем всю строчку и жмем сочетание клавиш Ctrl+Shift+Enter.

Поднимаемся на строку вверх и вводим в неё следующую формулу массива:

Жмем привычное уже нам сочетание клавиш для применения формулы массива.

Поднимаемся ещё на одну строку выше. В неё вводим формулу массива следующего вида:

Опять выделяем всю строку и применяем сочетание клавиш Ctrl+Shift+Enter.

Как видим, в Экселе систему уравнений можно решить целым рядом способов, каждый из которых имеет собственные преимущества и недостатки. Но все эти методы можно условно разделить на две большие группы: матричные и с применением инструмента подбора параметров. В некоторых случаях не всегда матричные методы подходят для решения задачи. В частности тогда, когда определитель матрицы равен нулю. В остальных же случаях пользователь сам волен решать, какой вариант он считает более удобным для себя.

Помимо этой статьи, на сайте еще 12704 инструкций.
Добавьте сайт Lumpics.ru в закладки (CTRL+D) и мы точно еще пригодимся вам.

Отблагодарите автора, поделитесь статьей в социальных сетях.

Видео:Решение системы уравнений в ExcelСкачать

учимся
программировать

Видео:2 Метод Гаусса в Calc Excel Решение системы линейных уравнений СЛАУСкачать

Программированию нельзя научить, можно только научится

Главная » Уроки по Численным методам » Урок 15. Решение СЛУ методом Крамера и методом Гаусса.

Видео:Метод Крамера для решения систем линейных алгебраических уравнений (СЛАУ) в ExcelСкачать

Урок 15. Решение СЛУ методом Крамера и методом Гаусса.

Видео:Решение системы линейных алгебраических уравнений (СЛАУ) в Excel МАТРИЧНЫМ МЕТОДОМСкачать

Метод Крамера

(СЛУ)
— определитель системы
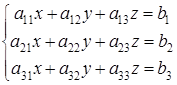
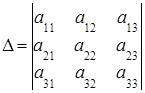
Если определитель СЛУ отличен от нуля, тогда решение системы определяется однозначно по формулам Крамера: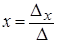
, , ()
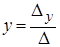
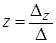
где:

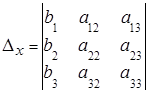	Для этого в столбец, где стоит переменная х, а значит в первый столбец, вместо коэффициентов при х, ставим свободные коэффициенты, которые в системе уравнений стоят в правых частях уравнений
	Для этого в столбец, где стоит переменная y (2 столбец), вместо коэффициентов при y, ставим свободные коэффициенты, которые в системе уравнений стоят в правых частях уравнений
	Для этого в столбец, где стоит переменная z, а значит втретий столбец, вместо коэффициентов при z, ставим свободные коэффициенты, которые в системе уравнений стоят в правых частях уравнений

Задание 1. Решить СЛУ с помощью формул Крамера в Excel

Ход решения

1. Запишем уравнение в матричном виде:

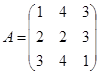
2. Введите матрицу А и В в Excel.

3. Найдите определитель матрицы А. Он должен получится равным 30.

4. Определитель системы отличен от нуля, следовательно — решение однозначно определяется по формулам Крамера.

5. Заполните значения dX, dY, dZ на листе Excel (см.рис.ниже).

6. Для вычисления значений dX, dY, dZ в ячейки F8, F12, F16 необходимо ввести функцию, вычисляющую определитель dX, dY, dZ соответственно.

7. Для вычисления значения X в ячейку I8 необходимо ввести формулу =F8/B5 (по формуле Крамера dX/|A|).

8. Самостоятельно введите формулы для вычисления Y и Z.

Задание 2: самостоятельно найти решение СЛУ методом Крамера:

Формулы Крамера и матричный метод решения систем линейных уравнений не имеют серьезного практического применения, так как связаны с громоздкими выкладками. Практически для решения систем линейных уравнений чаще всего применяется метод Гаусса.

Видео:Быстрое решение системы линейных уравнений в Excel.Скачать

Метод Гаусса

Процесс решения по методу Гаусса состоит из двух этапов.

1. Прямой ход: система приводится к ступенчатому (в частности, треугольному) виду.

Для того чтобы решить систему уравнений выписывают расширенную матрицу этой системы

и над строками этой матрицы производят элементарные преобразования, приводя ее к виду, когда ниже главной диагонали будут располагаться нули.
Разрешается выполнять элементарные преобразования над матрицами.
С помощью этих преобразований каждый раз получается расширенная матрица новой системы, равносильной исходной, т.е. такой системы, решение которой совпадает с решением исходной системы.

2. Обратный ход: идет последовательное определение неизвестных из этой ступенчатой системы.

Пример. Установить совместность и решить систему

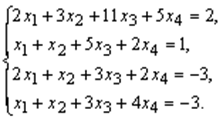
Решение.
Прямой ход: Выпишем расширенную матрицу системы и поменяем местами первую и вторую строки для того, чтобы элемент равнялся единице (так удобнее производить преобразования матрицы).

.

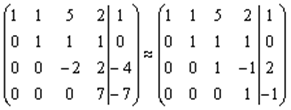
Имеем 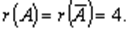Ранги матрицы системы и ее расширенной матрицы совпали с числом неизвестных. Согласно теореме Кронекера-Капелли система уравнений совместна и решение ее единственно.
Обратный ход: Выпишем систему уравнений, расширенную матрицу которой мы получили в результате преобразований:

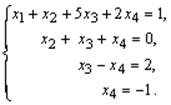
Итак, имеем .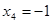
Далее, подставляя 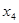в третье уравнение, найдем .
Подставляя и во второе уравнение, получим .
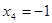
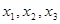
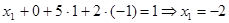
Подставляя в первое уравнение найденные получим .
Таким образом, имеем решение системы .

Видео:слау гаусс excelСкачать

Решение СЛУ методом Гаусса в Excel:

В тексте будет предлагаться ввести в диапазон ячеек формулу вида: и т.п., это так-называемые «формулы массива». Microsoft Excel автоматически заключает ее в фигурные скобки ( ). Для введения такого типа формул необходимо выделить весь диапазон, куда нужно вставить формулу, в первой ячейке ввести формулу без фигурных скобок (для примера выше – =A1:B3+$C$2:$C$3) и нажать Ctrl+Shift+Enter.
Пускай имеем систему линейных уравнений:

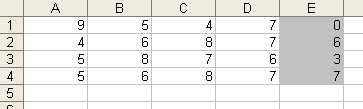
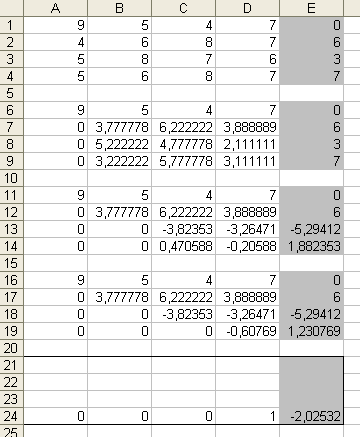
1. Запишем коэффициенты системы уравнений в ячейки A1:D4 а столбец свободных членов в ячейки E1:E4. Если в ячейке A1 находится 0, необходимо поменять строки местами так, чтоб в этой ячейке было отличное от ноля значение. Для большей наглядности можно добавить заливку ячеек, в которых находятся свободные члены.

2. Необходимо коэффициент при x1 во всех уравнениях кроме первого привести к 0. Для начала сделаем это для второго уравнения. Скопируем первую строку в ячейки A6:E6 без изменений, в ячейки A7:E7 необходимо ввести формулу: . Таким образом мы от второй строки отнимаем первую, умноженную на A2/$A$1, т.е. отношение первых коэффициентов второго и первого уравнения. Для удобства заполнения строк 8 и 9 ссылки на ячейки первой строки необходимо использовать абсолютные (используем символ $).

3. Копируем введенную формулу формулу в строки 8 и 9, таким образом избавляемся от коэффициентов перед x1 во всех уравнениях кроме первого.

4. Теперь приведем коэффициенты перед x2 в третьем и четвертом уравнении к 0. Для этого скопируем полученные 6-ю и 7-ю строки (только значения) в строки 11 и 12, а в ячейки A13:E13 введем формулу , которую затем скопируем в ячейки A14:E14. Таким образом реализуется разность строк 8 и 7, умноженных на коэффициент B8/$B$7. Не забываем проводить перестановку строк, чтоб избавиться от 0 в знаменателе дроби.

5. Осталось привести коэффициент при x3 в четвертом уравнении к 0, для этого вновь проделаем аналогичные действия: скопируем полученные 11, 12 и 13-ю строки (только значения) в строки 16-18, а в ячейки A19:E19 введем формулу . Таким образом реализуется разность строк 14 и 13, умноженных на коэффициент C14/$C$13. Не забываем проводить перестановку строк, чтоб избавиться от 0 в знаменателе дроби.

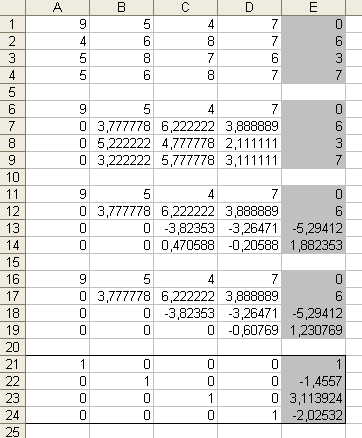
6. Прямая прогонка методом Гаусса завершена. Обратную прогонку начнем с последней строки полученной матрицы. Необходимо все элементы последней строки разделить на коэффициент при x4. Для этого в строку 24 введем формулу .

7. Приведем все строки к подобному виду, для этого заполним строки 23, 22, 21 следующими формулами:

23: – отнимаем от третьей строки четвертую умноженную на коэффициент при x4 третьей строки.

22: – от второй строки отнимаем третью и четвертую, умноженные на соответствующие коэффициенты.

21: – от первой строки отнимаем вторую, третью и четвертую, умноженные на соответствующие коэффициенты.

Результат (корни уравнения) вычислены в ячейках E21:E24.

🔍 Видео

Решение систем линейных уравнений методом простой итерации в ExcelСкачать

Решение системы уравнений методом Гаусса 4x4Скачать

Метод_Зейделя_ExcelСкачать

Решение систем линейных уравнений, урок 5/5. Итерационные методыСкачать

Простой Excel. Решение СЛАУ.Скачать

Решение системы уравнений методом ГауссаСкачать

Решение системы линейных уравнений методом ГауссаСкачать

Решение систем линейных уравнений, урок 2/5. Метод Крамера (метод определителей)Скачать

Математика без Ху!ни. Метод Гаусса.Скачать

Решение систем линейных уравнений, урок 3/5. Матричный методСкачать

Excel метод обратной матрицыСкачать