Системой m линейных уравнений с n неизвестными называется система вида
где aij и bi (i=1,…,m; b=1,…,n) – некоторые известные числа, а x1,…,xn – неизвестные. В обозначении коэффициентов aij первый индекс iобозначает номер уравнения, а второй j – номер неизвестного, при котором стоит этот коэффициент.
Коэффициенты при неизвестных будем записывать в виде матрицы 
Числа, стоящие в правых частях уравнений, b1,…,bm называются свободными членами.
Совокупность n чисел c1,…,cn называется решением данной системы, если каждое уравнение системы обращается в равенство после подстановки в него чисел c1,…,cn вместо соответствующих неизвестных x1,…,xn.
Наша задача будет заключаться в нахождении решений системы. При этом могут возникнуть три ситуации:
- Система может иметь единственное решение.
- Система может иметь бесконечное множество решений. Например,
. Решением этой системы является любая пара чисел, отличающихся знаком.
- И третий случай, когда система вообще не имеет решения. Например,
, если бы решение существовало, то x1 + x2 равнялось бы одновременно нулю и единице.
Система линейных уравнений, имеющая хотя бы одно решение, называется совместной. В противном случае, т.е. если система не имеет решений, то она называется несовместной.
Рассмотрим способы нахождения решений системы.
МАТРИЧНЫЙ МЕТОД РЕШЕНИЯ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ
Матрицы дают возможность кратко записать систему линейных уравнений. Пусть дана система из 3-х уравнений с тремя неизвестными:
Рассмотрим матрицу системы 
т.е. в результате произведения мы получаем левые части уравнений данной системы. Тогда пользуясь определением равенства матриц данную систему можно записать в виде

Здесь матрицы A и B известны, а матрица X неизвестна. Её и нужно найти, т.к. её элементы являются решением данной системы. Это уравнение называют матричным уравнением.
Пусть определитель матрицы отличен от нуля |A| ≠ 0. Тогда матричное уравнение решается следующим образом. Умножим обе части уравнения слева на матрицу A -1 , обратную матрице A: 
Заметим, что поскольку обратную матрицу можно найти только для квадратных матриц, то матричным методом можно решать только те системы, в которых число уравнений совпадает с числом неизвестных. Однако, матричная запись системы возможна и в случае, когда число уравнений не равно числу неизвестных, тогда матрица A не будет квадратной и поэтому нельзя найти решение системы в виде X = A -1 B.
Примеры. Решить системы уравнений.

Найдем матрицу обратную матрице A.

Таким образом, x = 3, y = – 1.
Решите матричное уравнение: XA+B=C, где
Выразим искомую матрицу X из заданного уравнения.
Найдем матрицу А -1 .
Решите матричное уравнение AX+B=C, где
Из уравнения получаем 
Следовательно,
Рассмотрим систему 3-х линейных уравнений с тремя неизвестными:
Определитель третьего порядка, соответствующий матрице системы, т.е. составленный из коэффициентов при неизвестных,
называется определителем системы.
Составим ещё три определителя следующим образом: заменим в определителе D последовательно 1, 2 и 3 столбцы столбцом свободных членов
Тогда можно доказать следующий результат.
Теорема (правило Крамера). Если определитель системы Δ ≠ 0, то рассматриваемая система имеет одно и только одно решение, причём
Доказательство. Итак, рассмотрим систему 3-х уравнений с тремя неизвестными. Умножим 1-ое уравнение системы на алгебраическое дополнение A11 элемента a11, 2-ое уравнение – на A21 и 3-е – на A31:
Сложим эти уравнения:
Рассмотрим каждую из скобок и правую часть этого уравнения. По теореме о разложении определителя по элементам 1-го столбца

Далее рассмотрим коэффициенты при x2:
Аналогично можно показать, что и 
Наконец несложно заметить, что
Таким образом, получаем равенство: 
Следовательно, 
Аналогично выводятся равенства 

Таким образом, заметим, что если определитель системы Δ ≠ 0, то система имеет единственное решение и обратно. Если же определитель системы равен нулю, то система либо имеет бесконечное множество решений, либо не имеет решений, т.е. несовместна.
Примеры. Решить систему уравнений

Решите систему уравнений при различных значениях параметра p:
Система имеет единственное решение, если Δ ≠ 0.


- При
- При p = 30 получаем систему уравнений
которая не имеет решений.
- При p = –30 система принимает вид
и, следовательно, имеет бесконечное множество решений x=y,y Î R.
Ранее рассмотренные методы можно применять при решении только тех систем, в которых число уравнений совпадает с числом неизвестных, причём определитель системы должен быть отличен от нуля. Метод Гаусса является более универсальным и пригоден для систем с любым числом уравнений. Он заключается в последовательном исключении неизвестных из уравнений системы.
Вновь рассмотрим систему из трёх уравнений с тремя неизвестными:

Первое уравнение оставим без изменения, а из 2-го и 3-го исключим слагаемые, содержащие x1. Для этого второе уравнение разделим на а21 и умножим на –а11, а затем сложим с 1-ым уравнением. Аналогично третье уравнение разделим на а31 и умножим на –а11, а затем сложим с первым. В результате исходная система примет вид:
Теперь из последнего уравнения исключим слагаемое, содержащее x2. Для этого третье уравнение разделим на 

Отсюда из последнего уравнения легко найти x3, затем из 2-го уравнения x2 и, наконец, из 1-го – x1.
При использовании метода Гаусса уравнения при необходимости можно менять местами.
Часто вместо того, чтобы писать новую систему уравнений, ограничиваются тем, что выписывают расширенную матрицу системы:
и затем приводят её к треугольному или диагональному виду с помощью элементарных преобразований.
К элементарным преобразованиям матрицы относятся следующие преобразования:
- перестановка строк или столбцов;
- умножение строки на число, отличное от нуля;
- прибавление к одной строке другие строки.
Примеры: Решить системы уравнений методом Гаусса.

Вернувшись к системе уравнений, будем иметь
Выпишем расширенную матрицу системы и сведем ее к треугольному виду.
Вернувшись к системе уравнений, несложно заметить, что третье уравнения системы будет ложным, а значит, система решений не имеет.
Разделим вторую строку матрицы на 2 и поменяем местами первый и третий столбики. Тогда первый столбец будет соответствовать коэффициентам при неизвестной z, а третий – при x.
Вернемся к системе уравнений.
Из третьего уравнения выразим одну неизвестную через другую и подставим в первое.
Таким образом, система имеет бесконечное множество решений.
Видео:Система уравнений не имеет решений или имеет бесчисленное множество решенийСкачать

Теорема Кронекера-Капелли
Совместная система линейных уравнений имеет единственное решение, если ранг этой системы равен количеству переменных.
Совместная система линейных уравнений имеет бесконечное множество решений, если ранг этой системы меньше количества переменных.
Пример №1 . Исследовать систему алгебраических уравнений (без непосредственного решения системы) с помощью теоремы Кронекера-Капелли.
Запишем систему в виде:
Для удобства вычислений поменяем строки местами:
Добавим 2-ую строку к 1-ой:
Добавим 3-ую строку к 2-ой:
Умножим 3-ую строку на (2). Добавим 4-ую строку к 3-ой:
Умножим 1-ую строку на (3). Умножим 2-ую строку на (-1). Добавим 2-ую строку к 1-ой:
Умножим 3-ую строку на (-1). Добавим 3-ую строку к 2-ой:
Добавим 2-ую строку к 1-ой:
Это соответствует системе:
-3x2 + 9x3 = 6
-4x1 + 5x2 + 7x3 — 10x4 = 0
За базисные переменные примем x1 и x2. Тогда свободные x3,x4.
Ранг основной матрицы равен 2. Ранг расширенной матрицы тоже равен 2. Система совместна и имеет бесконечное множество решений.
Пример №2 .
Запишем систему в виде:
Для удобства вычислений поменяем строки местами:
Умножим 2-ую строку на (-1). Добавим 2-ую строку к 1-ой:
Умножим 2-ую строку на (2). Умножим 3-ую строку на (-1). Добавим 3-ую строку к 2-ой:
Умножим 3-ую строку на (3). Умножим 4-ую строку на (-2). Добавим 4-ую строку к 3-ой:
Добавим 2-ую строку к 1-ой:
Умножим 3-ую строку на (-1). Добавим 3-ую строку к 2-ой:
Добавим 2-ую строку к 1-ой:
3x2 -2x3 – 3x4 = 10
3x1 -x2 -2x3 = 1
Необходимо переменные x3,x4 принять в качестве свободных переменных и через них выразить базисные – x1, x2.
Ранг основной матрицы равен 2. Ранг расширенной матрицы тоже равен 2. Система совместна и имеет бесконечное множество решений.
Пример №3 . Дана система линейных уравнений у которой число уравнений равно числу неизвестных. При каком условии эта система имеет единственное решение?
Ответ: Система имеет единственное решение, если ранг этой системы будет равен количеству переменных.
Видео:14. Метод Гаусса решения систем линейных уравнений ( бесконечное множество решений ). Часть 3Скачать

Системы линейных уравнений
Глава 5. Системы линейных уравнений
Определение. Матрицей называется прямоугольная таблица, составленная из чисел.
Числа, записанные в матрице, называются её элементами. При этом они могут быть как действительными, так и комплексными. Пример:
A =
Наша матрица A состоит из 3 строк и 4 столбцов. Будем записывать это так, что (3, 4) − размер матрицы A (иногда пишут 3×4, но × легко перепутать с x, особливо в рукописном тексте). Вообще, если в матрице s строк и n столбцов, то её размером считается запись (s, n). Матрицу обрамляют круглыми скобками: (). В литературе вы можете встретить другие обозначения: || || или []. Если s = n, то матрица называется квадратною. Матрицу размера (n, n) называют также квадратною матрицею n—го порядка.
Если надобно записать матрицу в общем (буквенном) виде, то пишут так:
A =
Это матрица размера (s, n), каждый её элемент обозначен одной и той же буквою − обыкновенно (хотя и не обязательно) это та же буква, которая обозначает самоё матрицу, но строчная. Эта буква снабжена двойными индексами: a11 − это не ‘a одиннадцать’, а ‘a один-один’. Первый индекс означает номер строки, в которой стоит данный элемент, второй − номер столбца. Разделителей между индексами обыкновенно не пишут, доколе это не может привести к неопределённости; к примеру, запись a211 непонятна: не то это a2,11, не то a21,1. В этом случае разделитель обязателен (здесь это запятая).
Среди всех матриц выделим матрицы, состоящие из одного столбца, т. е. размера (s, 1):

Такую матрицу назовём матрицей—столбцом, или вектор—столбцом. Аналогично матрицу вида
размера (1, n) назовём матрицей—строкой, или вектор—строкой.
5.1.2. Ступенчатая матрица
Определение 1. Строка матрицы называется нулевой строкой, если она состоит из одних нулей.
Определение 2. Главным элементом какой-либо ненулевой строки данной матрицы называется первый ненулевой элемент этой строки, считая слева направо.
Нулевая строка не имеет главного элемента, все остальные строки имеют однозначно определённый главный элемент. В любой матрице число главных элементов равно числу ненулевых строк.
Определение 3. Матрица называется ступенчатой, если для любых двух её последовательных строк выполняется одно из двух условий:
1) вторая строка состоит из одних нулей (нулевая строка);
2) обе строки ненулевые, и при этом главный элемент первой строки расположен строго левее главного элемента второй строки.
Из этого определения легко понять, что нулевые строки концентрируются в конце (внизу) матрицы, составляя нулевой блок (блок нулевых строк). В самом деле, если какая-либо строка нулевая, то в силу первой части определения все последующие строки также нулевые. Впрочем, нулевых строк может и вовсе не быть.
Определение 4. Матрица называется главной ступенчатой, если она является ступенчатой и сверх того
3) все главные элементы равны единице;
4) выше главных единиц (в тех же столбцах) стоят одни нули.
Из определения ясно, что каждый главный столбец главной ступенчатой матрицы устроен так, что в одной позиции стоит 1, а в остальных позициях − нули. (Ниже 1 стоят нули из-за того, что матрица является ступенчатой.) При этом номер позиции (строки), в которой стоит 1, равен номеру этого столбца в череде главных столбцов.
5.1.3. Элементарные преобразования
Определение 1. Элементарным преобразованием первого типа над строками какой-либо матрицы называется перестановка местами двух произвольных строк этой матрицы.
Определение 2. Элементарным преобразованием второго типа называется умножение произвольной строки данной матрицы на какое-либо число, не равное 0.
Определение 3. Элементарным преобразованием третьего типа называется прибавление к какой-либо строке данной матрицы другой строки, умноженной предварительно на любое число[1].
5.1.4. Теорема C. F. Gauss’а[2]
Теорема (C. F. Gauss’а). Любую матрицу с помощью нескольких элементарных преобразований над строками можно привести к главному ступенчатому виду.
Доказательство. Будем рассматривать матрицы размера (s, n). Обозначим через N сумму числа строк и столбцов: N = s + n. Доказательство поведём индукцией по этому параметру N. Наименьшее возможное значение N равно 2 (для матриц размера (1, 1)).
Основание (база) индукции. Пусть наша матрица A имеет размер (1, 1). Тогда A = = (a11). Если a11 = 0, то матрица уже главная ступенчатая. Если же нет, то разделим (единственную) строку матрицы A на a11, получим матрицу (1), которая уже является главной ступенчатой.
Индуктивный переход. Пусть теорема C. F. Gauss’а справедлива для любой матрицы, у которой s + n 1 вычтем из i-й строки матрицы D её первую строку, предварительно умножив её на число di1. После этой серии элементарных преобразований в новой матрице E все элементы первого столбца, кроме первого, станут равными нулю. Обозначим через F матрицу, получающуюся из E вычёркиванием первой строки и первого столбца. Её размеры меньше размеров матрицы A, и поэтому её можно привести к главному ступенчатому виду G с помощью серии элементарных преобразований над её строками, что равносильно совершению таких же элементарных преобразований над матрицей E. Пусть матрица E привелась таким образом к матрице H. Матрица H уже ступенчатая, но не обязательно главная ступенчатая. Возьмём какой-нибудь главный столбец матрицы G. Пусть главная единица нашего столбца стоит в k-й строке и l-м столбце матрицы H.
Вычтем из первой строки матрицы H её k-ю строку, умноженную предварительно на число h1l, и первый элемент нашего столбца обнулится. Важно, что при этом никак не затрагивается первый столбец, − он остаётся неизменным. Произведём указанную операцию с каждым главным столбцом матрицы G. Ясно, что новая матрица уже будет главной ступенчатой. Теорема доказана.
5.1.5. Обратимость элементарных преобразований
Предложение. Если над матрицей A совершено элементарное преобразование какого-либо типа, приводящее её к матрице B, то существует элементарное преобразование того же типа, приводящее матрицу B снова к матрице A.
Доказательство. Это очевидно для преобразований первого и второго типов. В самом деле, если мы совершили перестановку строк, то вторичная перестановка тех же строк вернёт нас к исходной матрице. Если мы умножили некоторую строку на ненулевое число, то умножение той же строки на обратное число вернёт нас к исходной матрице. Допустим теперь, что в данной матрице A мы прибавили к i-й строке j-ю строку (i ≠ j), предварительно умноженную на число α, и таким образом пришли к матрице B. Утверждаю, что можно вернуться к матрице A, если прибавить к i-й строке матрицы B её j-ю строку, предварительно умноженную на число −α. Так как при обоих преобразованиях все строки, кроме i-й, вообще не менялись, то достаточно посмотреть, что произойдёт с каким-нибудь элементом bik матрицы B. Вычисляем:
т. е. мы вернулись к матрице A, QED.
§ 5.2. Системы линейных уравнений
5.2.1. Основные определения
Определение 1. Система уравнений вида
называется системой линейных алгебраических уравнений с неизвестными x1, x2, …, xn.
Числа aij называются коэффициентами системы, bi − её свободными членами.
Определение 2. Решением системы (1) называется такой набор чисел 
Определение 3. Решить систему (1) − значит найти все её решения (множество всех решений).
Определение 4. Система (1) называется совместною, если она имеет хотя бы одно решение (множество всех решений непусто), и несовместною в противном случае, т. е. если она не имеет решений (множество всех решений пусто).
Определение 5. Система (1) называется определённою, если она имеет ровно одно решение, и неопределённою, если имеет более одного решения.
Мы очень скоро увидим, что неопределённая система имеет бесконечно много решений.
5.2.2. Элементарные преобразования над системами уравнений
Определение 1. Элементарным преобразованием первого типа над системой уравнений называется перестановка местами двух произвольных уравнений системы.
Определение 2. Элементарным преобразованием второго типа называется умножение любого уравнения системы на какое-либо число, не равное 0.
Определение 3. Элементарным преобразованием третьего типа называется прибавление к какому-либо уравнению другого уравнения, умноженного предварительно на любое число[3].
Каждой системе уравнений вида (1) можно поставить в соответствие две матрицы: матрицу системы и расширенную матрицу системы.
Определение 4. Матрицей системы уравнений (1) называется матрица, составленная из коэффициентов системы:

Определение 5. Расширенной матрицей системы уравнений (1) называется матрица, составленная из коэффициентов системы и свободных членов:

Иногда в расширенной матрице отделяют столбец свободных членов вертикальной чертой (сплошной или прерывистой), но это не обязательно. Ясно, что матрица системы не даёт полной информации о системе в отличие от расширенной матрицы, по которой можно однозначно восстановить систему уравнений, если только мы знаем список неизвестных (буквы, которыми были обозначены неизвестные). Впрочем, последнее не так существенно, потому что ведь мы в первую очередь интересуемся решениями, а каждое решение представляет собою просто набор чисел без обозначений неизвестных.
Определение 6. Пусть даны две системы уравнений относительно одного и того же набора неизвестных x1, x2, …, xn. Говорят, что система (2) является следствием системы (1), если каждое решение системы (1) является решением системы (2).
Другими словами, множество всех решений системы (1) есть подмножество (часть) множества всех решений системы (2).
Определение 7. Две системы уравнений относительно одного и того же набора неизвестных x1, x2, …, xn называются эквивалентными, или равносильными, если множества их решений совпадают, или, что то же, каждая из них является следствием другой.
Иными словами, две системы эквивалентны тогда и только тогда, когда каждое решение первой системы является решением второй и, наоборот, каждое решение второй системы является решением первой.
Предложение. При совершении одного элементарного преобразования система уравнений переходит в эквивалентную систему.
Доказательство. Достаточно доказать, что вторая система является следствием первой. Действительно, предположив, что это уже доказано, совершим обратное элементарное преобразование, которое вернёт нас к исходной системе (см. п. 5.1.5). По доказанному первая система тогда будет следствием второй, и всё доказано.
Докажем, что вторая система является следствием первой. Для преобразований первых двух типов это совершенно очевидно. Совершим преобразование третьего типа, прибавив к i-й строке j-ю строку, умноженную предварительно на число α. При этом изменится только i-е уравнение, поэтому я здесь выпишу только его:
Пусть 
Если подставить наше решение в новую систему, то все равенства, кроме i-го, будут выглядеть точно так же и поэтому выполняются. i-е же равенство будет выглядеть так:
Чтобы убедиться, что оно тоже выполняется, достаточно взять i-е равенство системы (1*) верных числовых равенств и прибавить к нему j-е равенство той же системы, предварительно умножив его на α. Предложение доказано.
5.2.3. Теорема C. F. Gauss’а (о системах линейных уравнений)
Лемма. Если в системе линейных уравнений совершить одно элементарное преобразование, то расширенная матрица новой системы может быть получена из расширенной матрицы старой системы с помощью совершения аналогичного (точно такого же, я буду говорить одноимённого) преобразования.
Доказательство: это очевидно.
Следствие. Если в расширенной матрице A системы линейных уравнений (1) совершить одно элементарное преобразование над её строками и таким образом прийти к новой матрице B, а затем одноимённое преобразование совершить над системой уравнений (1), то расширенная матрица новой системы (2) совпадёт с матрицей B.
Доказательство. В силу леммы расширенная матрица системы (2) может быть получена из матрицы A, т. е. расширенной матрицы системы (1), с помощью совершения преобразования, одноимённого тому, которое было совершено нами над системой уравнений (1). С другой стороны, это последнее преобразование было одноимённо тому, которое мы совершили над матрицей A. Таким образом, расширенная матрица системы (2) может быть получена из A с помощью того же самого преобразования, которое мы в самом начале совершили над матрицей A. Значит, эта новая расширенная матрица совпадает с B, QED.
Теорема (C. F. Gauss’а, о системах линейных уравнений). Всякая система линейных уравнений с помощью конечного числа элементарных преобразований может быть приведена к такой системе уравнений, расширенная матрица которой является главной ступенчатой.
Доказательство. Приведём расширенную матрицу данной системы уравнений с помощью серии элементарных преобразований над её строками к главному ступенчатому виду. Теперь будем совершать над самой данной системой одноимённые преобразования. По следствию из леммы на каждом этапе очередная матрица будет расширенной матрицей соответствующей системы уравнений. Значит, и последняя, главная ступенчатая, матрица будет служить расширенной матрицей последней системы, QED.
Важно, что на каждом этапе в силу предложения из предыдущего пункта система уравнений переходит в эквивалентную. На этом основан метод C. F. Gauss’а решения систем, при котором система приводится с помощью серии элементарных преобразований к главному ступенчатому виду. Множество всех решений системы при этом не меняется, так что достаточно решить последнюю систему. А системы, имеющие главный ступенчатый вид, решаются очень легко, как будет видно из следующего пункта.
5.2.4. Решение ступенчатых систем уравнений
Рассмотрим систему линейных уравнений, расширенная матрица которой является главной ступенчатой. Допуская известную вольность речи, будем такие системы называть ступенчатыми.
Определение. В ступенчатой системе уравнений неизвестные, соответствующие главным столбцам, называются главными неизвестными, все остальные − свободными неизвестными.
Здесь надлежит различать три случая.
1°. Столбец свободных членов является главным. В этом случае система несовместна.
В самом деле, пусть главный элемент последнего столбца расширенной матрицы (т. е. столбца свободных членов) находится в i-й строке. Тогда i-е уравнение имеет следующий вид:
(Напомню, что все главные элементы главной ступенчатой матрицы равны 1, а левее любого главного элемента всегда стоят одни нули.) Ясно, что такое уравнение не имеет решений, тем более не может иметь решений вся наша система.
2°. Все столбцы, кроме последнего, главные. (Другими словами: нет свободных неизвестных, а столбец свободных членов не является главным, т. е. не содержит главных элементов.) В этом случае в i-м столбце на i-м месте стоит 1 (i ≤ n), на остальных местах − нули. После отбрасывания нулевых уравнений придём к эквивалентной системе, которая в нашем случае приобретает следующий вид:
Ясно, что такая система имеет решение, и притом единственное, а именно, 
3°. Есть свободные неизвестные, но столбец свободных членов не является главным. Покажем, что в этом случае система имеет бесконечно много решений (и, следовательно, является неопределённой). Отбросим в расширенной матрице нулевые строки (они сосредоточены внизу матрицы), что приведёт к эквивалентной системе. Можно считать, что исходная расширенная матрица не была нулевой (для нулевой матрицы доказываемое утверждение очевидно), так что хотя бы одна строка останется. Теперь число строк в матрице равно числу главных неизвестных. Для удобства переобозначим неизвестные: пусть y1, y2, …, yr − главные неизвестные, а z1, z2, …, zn−r − свободные. Разнесём теперь неизвестные в разные части: главные неизвестные оставим в левых частях уравнений, а свободные перенесём в правые части, естественно, с противоположным знаком (свободные члены также остаются в правых частях). Получится система, эквивалентная исходной, следующего вида:
Мы видим, что здесь все главные неизвестные явно выражены через свободные, причём эти выражения (правые части) представляют собою линейные функции, т. е. линейные комбинации свободных неизвестных плюс свободный член. Как же решить получившуюся систему? Придадим свободным неизвестным произвольные значения и вычислим по написанным формулам соответствующие значения главных неизвестных. Очевидно, что в совокупности мы получим решение нашей системы. Более того, каждое решение можно получить таким способом при подходящем выборе свободных неизвестных, так как все неизвестные всегда будут связаны соотношениями (3). В этом смысле формулы (3) описывают множество всех решений нашей системы, т. е задают, как говорят, её общее решение. И ясно, что решений будет бесконечно много, потому что хотя бы одно свободное неизвестное у нас есть, значит, придать определённые значения свободным неизвестным мы можем бесконечным числом различных способов, и получающиеся решения будут различны.
Попутно мы фактически доказали следующие два утверждения.
Теорема 1 (критерий совместности ступенчатой системы). Система уравнений, расширенная матрица которой имеет главный ступенчатый вид, совместна тогда и только тогда, когда столбец свободных членов не является главным.
Теорема 2. Если система линейных уравнений имеет более одного решения, то она имеет бесконечно много решений.
Таким образом, линейная система не может иметь, например, ровно семь решений.
5.2.5. Однородные системы уравнений
Так называются системы линейных уравнений, в которых все свободные члены равны нулю:
Такая система всегда совместна, т. к. она всегда имеет решение 
Теорема. Если в однородной системе линейных уравнений (4) число уравнений s строго меньше числа неизвестных n, то такая система имеет хотя бы одно нетривиальное решение.
Доказательство. Приведём нашу систему к главному ступенчатому виду. На всех этапах однородность, очевидно, сохраняется. После отбрасывания нулевых уравнений мы получим однородную систему уравнений, эквивалентную исходной. Число её уравнений строго меньше числа неизвестных, так как число неизвестных не изменилось, а число уравнений даже могло уменьшиться. Но число строк теперь равно числу главных элементов, а значит, числу главных столбцов и числу главных неизвестных. Таким образом, число главных неизвестных строго меньше общего числа неизвестных. Значит, есть свободные неизвестные, а тогда система неопределённая (нулевой столбец свободных членов не может быть главным) и имеет бесконечно много решений. Значит, есть и ненулевые решения, QED.
[1] При этом результат ставится в первую из этих двух строк, а вторая из них, равно как и все остальные строки матрицы, не меняется.
[2] ́дрих Га́усс (нем. Johann Carl Friedrich Gauß; 30 апреля 1777, Брауншвейг − 23 февраля 1855, Гёттинген) − великий немецкий математик, астроном и физик, считается одним из величайших математиков всех времён.
[3] При этом результат ставится на место первого из этих двух уравнений, а второе из них, равно как и все остальные, не меняется.
🎦 Видео
Решение системы уравнений методом Гаусса. Бесконечное множество решенийСкачать

Теорема о количестве решений системы линейных уравненийСкачать

Математика без Ху!ни. Метод Гаусса. Совместность системы. Ранг матрицы.Скачать

15. Однородная система линейных уравнений / фундаментальная система решенийСкачать

#75 Урок 36. Определение количества решений системы уравнений. Алгебра 7 класс.Скачать

Алгебраическое определение количества решений системы линейных уравнений | Алгебра IСкачать

Когда система имеет бесконечное количество решенийСкачать

Система линейных уравнений. Общее решение. Метод ГауссаСкачать

Метод Крамера за 3 минуты. Решение системы линейных уравнений - bezbotvyСкачать

Неоднородные системы линейных уравненийСкачать
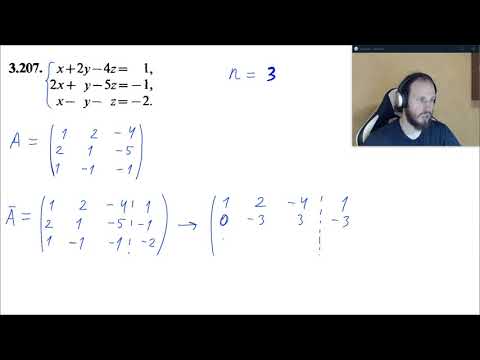
Общее, частное, базисное решение системы линейных уравнений Метод ГауссаСкачать

Лекция 12. Системы линейных уравненийСкачать

Решение системы линейных однородных уравнений (№726)Скачать

Система линейных уравнений. Графическое решение системы | Алгебра 7 класс #45 | ИнфоурокСкачать

метод Гаусса СИСТЕМА ЛИНЕЙНЫХ УРАВНЕНИЙ решение СЛАУСкачать

Матричный метод решения систем уравненийСкачать

13 Исследование систем линейных уравненийСкачать

Неоднородная система линейных уравненийСкачать


 . Решением этой системы является любая пара чисел, отличающихся знаком.
. Решением этой системы является любая пара чисел, отличающихся знаком. , если бы решение существовало, то x1 + x2 равнялось бы одновременно нулю и единице.
, если бы решение существовало, то x1 + x2 равнялось бы одновременно нулю и единице.





















 которая не имеет решений.
которая не имеет решений. и, следовательно, имеет бесконечное множество решений x=y,y Î R.
и, следовательно, имеет бесконечное множество решений x=y,y Î R.



















