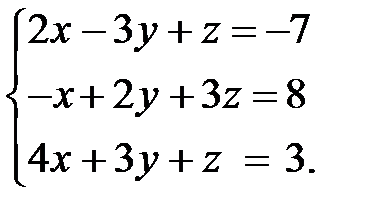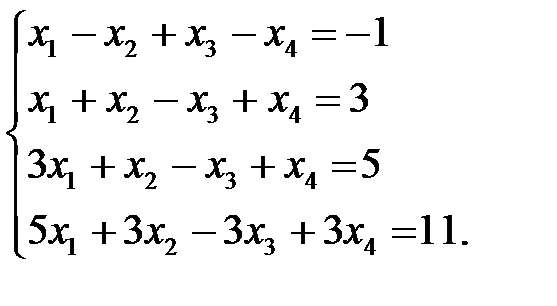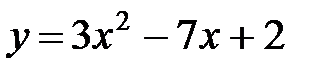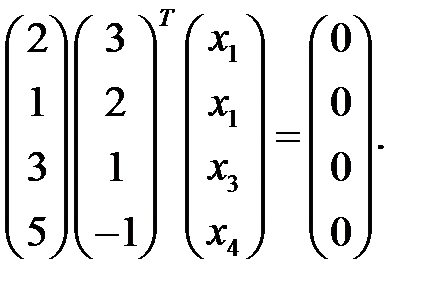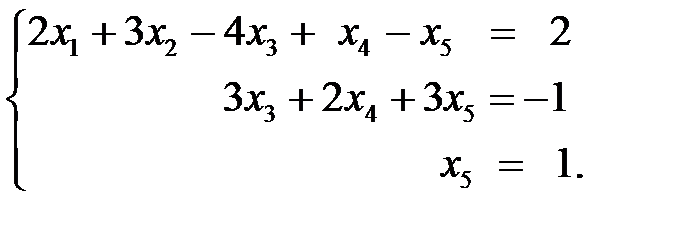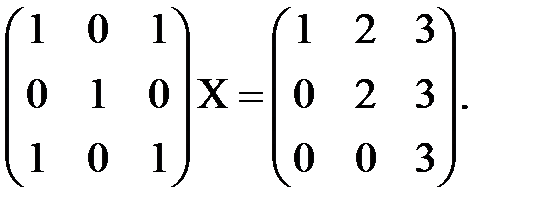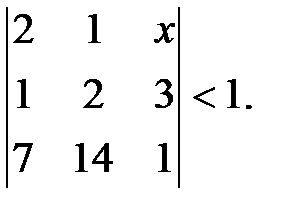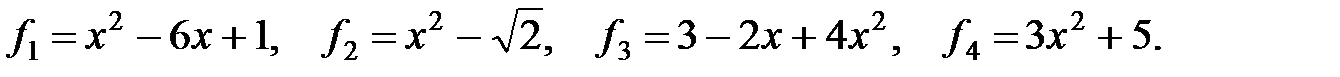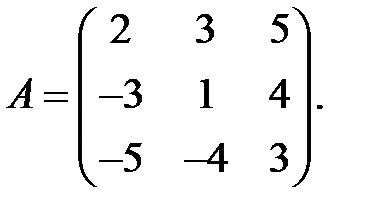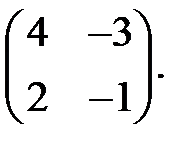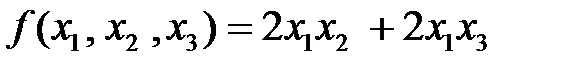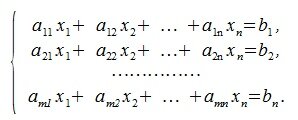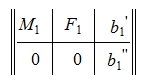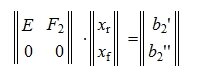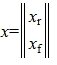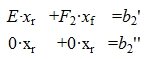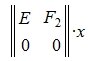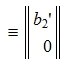ЛИНЕЙНАЯ АЛГЕБРА
ИнЭИ
1 семестр, 2 2 , 2019/20 20 уч. год
ЭКЗАМЕНАЦИОННАЯ ПРОГРАММА
1. Матрицы. Виды матриц. Равенство матриц, сложение, умножение матрицы на число. Основные свойства.
2. Умножение матриц и его свойства. Транспонирование матриц и его свойства.
3. Определители. Свойства определителей.
4. Обратная матрица. Единственность. Существование и вычисление обратной матрицы (через построение присоединенной матрицы).
5. Ранг матрицы. Элементарные преобразования строк матрицы. Теорема о том, что элементарные преобразования не меняют ранга.
6. Приведение матрицы к ступенчатому виду элементарными преобразованиями. Ранг ступенчатой матрицы.
7. Пространство R n арифметических векторов. Линейно зависимые и независимые векторы.
8. Критерий линейной зависимости векторов R n . Следствие из этой теоремы. Понятие базиса.
9. Теоремы о базисах в R n . Стандартный базис.
10. Теорема о базисном миноре.
11. Системы линейных уравнений. Метод Гаусса.
12. Квадратные системы линейных уравнений. Формулы Крамера.
13. Однородные системы линейных уравнений. Условия нетривиальной совместности. Свойства решений.
14. Фундаментальная система решений однородной системы. Структура общего решения.
15. Неоднородные системы. Структура общего решения. Теорема Кронекера–Капелли.
16. Геометрические векторы. Коллинеарность и компланарность. Равенство векторов. Арифметические действия с векторами. Координаты вектора в декартовой системе координат.
17. Скалярное произведение векторов и его свойства. Вычисление через координаты в прямоугольной системе координат. Критерий перпендикулярности.
18. Векторное произведение векторов и его свойства. Вычисление через координаты в прямоугольной системе координат. Критерий коллинеарности.
19. Смешанное произведение векторов. Вычисление через координаты в прямоугольной системе координат. Критерий компланарности.
20. Общее уравнение плоскости. Геометрический смысл коэффициентов. Взаимное расположение пары плоскостей.
21. Каноническое и параметрическое уравнения прямой. Прямая как пересечение плоскостей. Взаимное расположение пары прямых.
22. Взаимное расположение прямой и плоскости в пространстве.
23. Линейные пространства. Размерность и базис. Подпространства.
24. Примеры линейных пространств.
25. Евклидовы пространства. Неравенство Коши–Буняковского.
26. Процесс ортогонализации и существование в евклидовом пространстве ортонормированных базисов.
27. Линейный оператор и его матрица. Матричная форма записи линейного оператора.
28. Образ, ядро, ранг и дефект оператора.
29. Изменение координат вектора и матрицы оператора при переходе к другому базису.
30. Сопряженный и самосопряженный операторы. Матрицы этих операторов в ортонормированном базисе.
31. Собственные векторы и собственные значения линейных операторов и их свойства.
32. Характеристический многочлен и его инвариантность.
33. Собственные базисы. Существование собственного ортонормированного базиса у самосопряженного оператора.
34. Квадратичная форма и ее матрица. Приведение к каноническому виду ортогональным преобразованием. Закон инерции.
35. Уравнения кривых 2-го порядка в канонических системах координат. Классификация.
36. Уравнения поверхностей 2-го порядка в канонических системах координат (основные типы).
1.Используя формулы Крамера, решить систему уравнений:
2. Решить систему уравнений:
3.Дан вектор 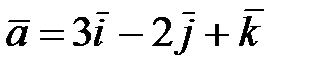
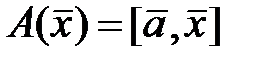
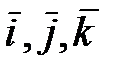
4. Определить тип кривой 2-го порядка:
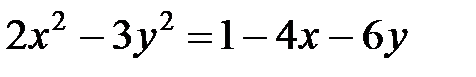
5. Чему равен фокальный параметр параболы:
6.Можно ли столбцы матрицы 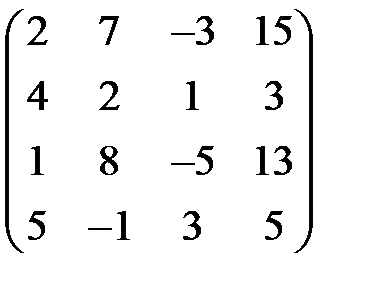
7. Вектор 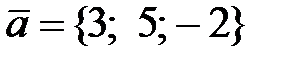
8. Найти фундаментальную систему решений системы уравнений:
9.Дан оператор 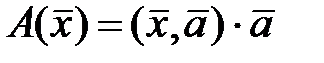
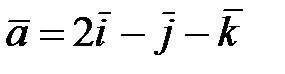
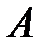
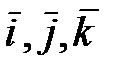
10.Решить систему уравнений:
11. Выяснить, существует ли такая матрица 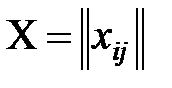
12. Решить неравенство:
13.В пространстве функций, заданных на 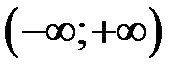
Является ли они линейно независимыми?
14. Указать хотя бы один базис в подпространстве:
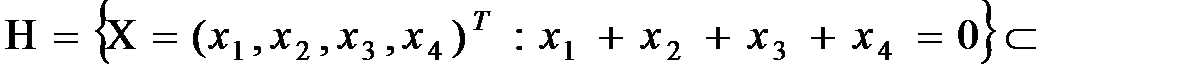
15. В треугольнике с вершинами O(0,0,0), A(7,3,–5), B(–5,7,3) проведена биссектриса 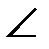
16. Система линейных уравнений AX = B несовместна, RgA=10. Чему равен Rg(A/B)?
17. В базисе 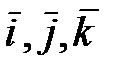
Может ли образ 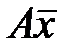
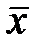
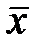
18. Векторы 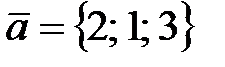
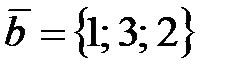
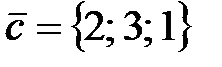
19. Найти собственные значения оператора, заданного матрицей
20. Найти все векторы, координаты которых не меняются при переходе от базиса 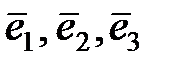
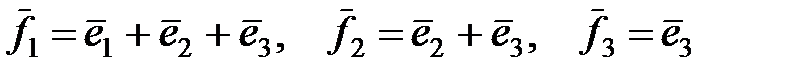
21. Скалярное произведение векторов 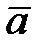
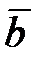
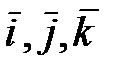
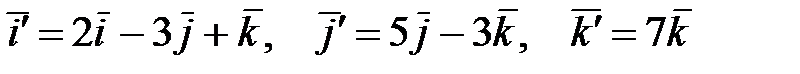
22. Оператор задан своей матрицей 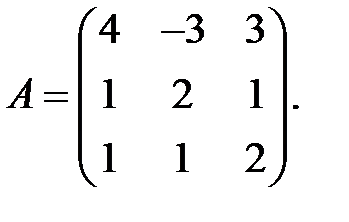
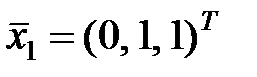
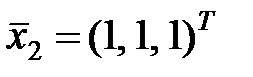
23. Привести квадратичную форму
к каноническому виду ортогональным преобразованием (само преобразование не указывать).
24. Линейная система пяти уравнений с семью неизвестными AX = B такова, что RgA=5. Доказать, что она совместна при любой правой части В.
25.Векторы 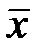
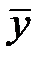
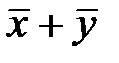
26.Оператор А в базисе 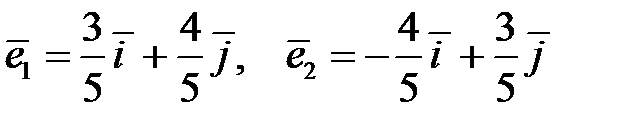
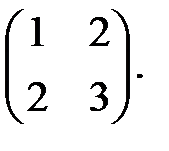
- Теорема Кронекера-Капелли. Исследование систем линейных уравнений на совместность. Первая часть.
- Способ №1. Вычисление рангов по определению.
- Способ №2. Вычисление ранга методом элементарных преобразований.
- Система линейных уравнений. Общее решение
- Нахождение общего решения системы линейных уравнений
- Нахождение общего решения системы линейных уравнений с помощью псевдообратной матрицы
- 💡 Видео
Видео:Исследование систем линейных уравнений на совместностьСкачать

Теорема Кронекера-Капелли. Исследование систем линейных уравнений на совместность. Первая часть.
Исследовать систему линейных агебраических уравнений (СЛАУ) на совместность означает выяснить, есть у этой системы решения, или же их нет. Ну и если решения есть, то указать сколько их.
Нам понадобятся сведения из темы «Система линейных алгебраических уравнений. Основные термины. Матричная форма записи». В частности, нужны такие понятия, как матрица системы и расширенная матрица системы, поскольку именно на них опирается формулировка теоремы Кронекера-Капелли. Как обычно, матрицу системы будем обозначать буквой $A$, а расширенную матрицу системы – буквой $widetilde$.
Система линейных алгебраических уравнений совместна тогда и только тогда, когда ранг матрицы системы равен рангу расширенной матрицы системы, т.е. $rang A=rangwidetilde$.
Следствие из теоремы Кронекера-Капелли
Заметьте, что сформулированная теорема и следствие из неё не указывают, как найти решение СЛАУ. С их помощью можно лишь выяснить, существуют эти решения или нет, а если существуют – то сколько.
Исследовать СЛАУ $ left <begin& -3x_1+9x_2-7x_3=17;\ & -x_1+2x_2-4x_3=9;\ & 4x_1-2x_2+19x_3=-42. endright.$ на совместность. Если СЛАУ совместна, указать количество решений.
Чтобы выяснить наличие решений заданной СЛАУ, используем теорему Кронекера-Капелли. Нам понадобятся матрица системы $A$ и расширенная матрица системы $widetilde$, запишем их:
Видео:Решение системы линейных уравнений. Подстановка. С дробными выражениями.Скачать

Способ №1. Вычисление рангов по определению.
Согласно определению, ранг – это наивысший порядок миноров матрицы, среди которых есть хоть один, отличный от нуля. Обычно исследование начинают с миноров первого порядка, но здесь удобнее приступить сразу к вычислению минора третьего порядка матрицы $A$. Элементы минора третьего порядка находятся на пересечении трёх строк и трёх столбцов рассматриваемой матрицы. Так как матрица $A$ содержит всего 3 строки и 3 столбца, то минор третьего порядка матрицы $A$ – это определитель матрицы $A$, т.е. $Delta A$. Для вычисления определителя применим формулу №2 из темы «Формулы для вычисления определителей второго и третьего порядков»:
$$ Delta A=left| begin -3 & 9 & -7 \ -1 & 2 & -4 \ 4 & -2 & 19 end right|=-21. $$
Итак, есть минор третьего порядка матрицы $A$, который не равен нулю. Минор четвёртого порядка составить невозможно, так как для него требуется 4 строки и 4 столбца, а в матрице $A$ всего 3 строки и 3 столбца. Итак, наивысший порядок миноров матрицы $A$, среди которых есть хотя бы один не равный нулю, равен 3. Следовательно, $rang A=3$.
Задача решена. Какие недостатки и преимущества имеет данный способ? Для начала поговорим о плюсах. Во-первых, нам понадобилось найти всего один определитель. После этого мы сразу сделали вывод о количестве решений. Обычно в стандартных типовых расчётах даются системы уравнений, которые содержат три неизвестных и имеют единственное решение. Для таких систем данный метод очень даже удобен, ибо мы заранее знаем, что решение есть (иначе примера не было бы в типовом расчёте). Т.е. нам остаётся только показать наличие решения наиболее быстрым способом. Во-вторых, вычисленное значение определителя матрицы системы (т.е. $Delta A$) пригодится после: когда станем решать заданную систему методом Крамера или с помощью обратной матрицы.
Однако метод вычисления ранга по определению нежелательно применять, если матрица системы $A$ является прямоугольной. В этом случае лучше применить второй метод, о котором пойдёт речь ниже. Кроме того, если $Delta A=0$, то мы ничего не сможем сказать о количестве решений заданной неоднородной СЛАУ. Может, СЛАУ имеет бесконечное количество решений, а может – ни одного. Если $Delta A=0$, то требуется дополнительное исследование, которое зачастую является громоздким.
Подводя итог сказанному, отмечу, что первый способ хорош для тех СЛАУ, у которых матрица системы квадратна. При этом сама СЛАУ содержит три или четыре неизвестных и взята из стандартных типовых расчетов или контрольных работ.
Видео:Математика без Ху!ни. Метод Гаусса. Совместность системы. Ранг матрицы.Скачать

Способ №2. Вычисление ранга методом элементарных преобразований.
Какие преимущества второго способа? Главное преимущество – это его универсальность. Нам совершенно неважно, является ли матрица системы квадратной или нет. Кроме того, мы фактически провели преобразования прямого хода метода Гаусса. Осталось лишь пару действий, и мы смогли бы получить решение данной СЛАУ. Честно говоря, второй способ нравится мне более первого, но выбор – это дело вкуса.
Ответ: Заданная СЛАУ совместна и определена.
$$ left( begin 1 & -1 & 2 & -1\ -1 & 2 & -3 & 3 \ 2 & -3 & 5 & -4 \ 3 & -2 & 5 & 1 \ 2 & -1 & 3 & 2 end right) begin phantom\r_2+r_1\r_3-2r_1\ r_4-3r_1\r_5-2r_1endrightarrow left( begin 1 & -1 & 2 & -1\ 0 & 1 & -1 & 2 \ 0 & -1 & 1 & -2 \ 0 & 1 & -1 & 4 \ 0 & 1 & -1 & 4 end right) begin phantom\phantom\r_3-r_2\ r_4-r_2\r_5+r_2endrightarrow\ $$ $$ rightarrowleft( begin 1 & -1 & 2 & -1\ 0 & 1 & -1 & 2 \ 0 & 0 & 0 & 2 \ 0 & 0 & 0 & 2 \ 0 & 0 & 0 & 0 end right) begin phantom\phantom\phantom\ r_4-r_3\phantomendrightarrow left( begin 1 & -1 & 2 & -1\ 0 & 1 & -1 & 2 \ 0 & 0 & 0 & 2 \ 0 & 0 & 0 & 0 \ 0 & 0 & 0 & 0 end right) $$
Расширенная матрица системы приведена к ступенчатому виду. Ранг ступенчатой матрицы равен количеству её ненулевых строк, поэтому $rangwidetilde=3$. Матрица $A$ (до черты) тоже приведена к ступенчатому виду, и ранг её равен 2, $rang=2$.
Ответ: система несовместна.
Приводим расширенную матрицу системы к ступенчатому виду:
$$ left( begin 2 & 0 & 7 & -5 & 11 & 42\ 1 & -2 & 3 & 0 & 2 & 17 \ -3 & 9 & -11 & 0 & -7 & -64 \ -5 & 17 & -16 & -5 & -4 & -90 \ 7 & -17 & 23 & 0 & 15 & 132 end right) overset<r_1leftrightarrow> $$ $$ rightarrowleft( begin 1 & -2 & 3 & 0 & 2 & 17\ 2 & 0 & 7 & -5 & 11 & 42\ -3 & 9 & -11 & 0 & -7 & -64\ -5 & 17 & -16 & -5 & -4 & -90 \ 7 & -17 & 23 & 0 & 15 & 132 end right) begin phantom\ r_2-2r_1 \r_3+3r_1 \ r_4+5r_1 \ r_5-7r_1 end rightarrow left( begin 1 & -2 & 3 & 0 & 2 & 17\ 0 & 4 & 1 & -5 & 7 & 8\ 0 & 3 & -2 & 0 & -1 & -13\ 0 & 7 & -1 & -5 & 6 & -5 \ 0 & -3 & 2 & 0 & 1 & 13 end right) begin phantom\ phantom\4r_3+3r_2 \ 4r_4-7r_2 \ 4r_5+3r_2 end rightarrow $$ $$ rightarrowleft( begin 1 & -2 & 3 & 0 & 2 & 17\ 0 & 4 & 1 & -5 & 7 & 8\ 0 & 0 & -11 & 15 & -25 & -76\ 0 & 0 & -11 & 15 & -25 & -76 \ 0 & 0 & 11 & -15 & 25 & 76 end right) begin phantom\ phantom\phantom \ r_4-r_3 \ r_5+r_2 end rightarrow left( begin 1 & -2 & 3 & 0 & 2 & 17\ 0 & 4 & 1 & -5 & 7 & 8\ 0 & 0 & -11 & 15 & -25 & -76\ 0 & 0 & 0 & 0 & 0 & 0 \ 0 & 0 & 0 & 0 & 0 & 0 end right) $$
Мы привели расширенную матрицу системы и саму матрицу системы к ступенчатому виду. Ранг расширенной матрицы системы равен трём, ранг матрицы системы также равен трём. Так как система содержит $n=5$ неизвестных, т.е. $rangwidetilde=ranglt$, то согласно пункту №2 следствия из теоремы Кронекера-Капелли данная система является неопределённой, т.е. имеет бесконечное количество решений.
Ответ: система является неопределённой.
Во второй части мы разберём примеры, которые нередко включают в типовые расчёты или контрольные работы по высшей математике: исследование на совместность и решение СЛАУ в зависимости от значений параметров, входящих в неё.
Видео:ПОСМОТРИ это видео, если хочешь решить систему линейных уравнений! Метод ПодстановкиСкачать

Система линейных уравнений. Общее решение
Система линейных уравнений (СЛУ) может быть записана в виде
где m, n натуральные числа, aij (i= 1,2, . m, j= 1,2. n) называются коэффициентами, bi (i= 1,2. m) называются свободными членами, xi (i= 1,2. n) называются неизвестными.
Систему линейных уравнений (1) можно записать в виде
где A матрица порядка m×n , x — вектор порядка n (x∈R n ), b — вектор порядка m (b ∈R m ).
Решением системы (2) называется выбор такого вектора x’, что выполнено равенство
Если система линейных уравнений имеет хотя бы одно решение, то СЛУ называется совместным.
Если СЛУ не имеет решения, то СЛУ называется несовместным.
Если СЛУ имеет единственное решение, то СЛУ называется определенным.
Если СЛУ имеет более одного решения, то СЛУ называется неопределенным.
Система линейных уравнений (2) называется неоднородной cистемой линейных уравнений, если b≠0.
Система линейных уравнений (2) называется однородной cистемой линейных уравнений, если b=0.
Видео:Решение систем уравнений методом подстановкиСкачать

Нахождение общего решения системы линейных уравнений
Общее решение системы линейных уравнений (1)((или (2))− это множество всех решений этой системы.
Пусть A m×n — матрица rankA=r. В общем случае можем предположить что r 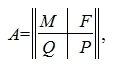
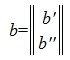
Применяя метод исключения Гаусса для системы (3), получим:
где M1 верхняя треугольная матрица, 0 — нулевые матрицы соответствующих порядков. Далее, применяя обратный ход исключения Гаусса, и, далее, разделив элементы каждой строки на ведущий элемент этой строки (если ведущий элемент существует) получим:
где E — единичная матрица порядка r×r.
Запишем (5) в виде системы линейных уравнений:
где
Решим систему линейных уравнений (6). Для этого перезапишем в следующем виде:
Из второго уравнения системы (7) следует, что для совместности системы (6) и, следовательно, (2) (или (1)) должно выполняться условие b2»≡ 0. Если система совместна, то решаем первое уравнение системы (7) относительно вектора xr:
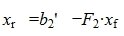 | (8) |
Таким образом первые r координаты вектора x 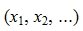
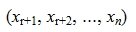
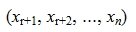
Найдем, далее, множество всех векторов x, удовлетворяющих уравнению (6) и, следовательно, (2)( или (1)).
Рассмотрим множество всех векторов х, удовлетворяющих условию
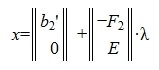 | (9) |
где λ — произвольный вектор-столбец длины n-r.
Подставляя (9) в (6) получим:
Следовательно (9) является решением системы (6) и, следовательно, (2)(или (1)). Отметим что вектор 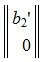
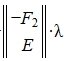
Видео:Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

Нахождение общего решения системы линейных уравнений с помощью псевдообратной матрицы
Обозначим через R(A) пространство столбцов матрицы A, т.е.
1. Пусть A n×n матрица и rank(A)=n. Тогда существует обратная к A матрица A -1 , и следовательно единственное решение СЛУ (2) примет вид:
Действительно, подставляя (3) в (2) имеем:
2. Пусть A m×n − матрица, rank(A)=r.
💡 Видео
Система линейных уравнений. Метод обратной матрицы. Матричный метод.Скачать

Решение системы линейных уравнений с двумя переменными способом подстановки. 6 класс.Скачать

МЕТОД ПОДСТАНОВКИ 😉 СИСТЕМЫ УРАВНЕНИЙ ЧАСТЬ I#математика #егэ #огэ #shorts #профильныйегэСкачать

Решение системы линейных уравнений графическим методом. 7 класс.Скачать

Решение системы неравенствСкачать

Неоднородные системы линейных уравненийСкачать
9 класс, 11 урок, Методы решения систем уравненийСкачать

9 класс, 12 урок, Однородные системы. Симметрические системыСкачать

Система с тремя переменнымиСкачать

Система уравнений VS Система неравенств. ОГЭ по математике №9, 13| Математика TutorOnlineСкачать

Решение систем уравнений. Методом подстановки. Выразить YСкачать

Решение систем уравнений второго порядка. 8 класс.Скачать

Математика | Система уравнений на желтую звездочку (feat Золотой Медалист по бегу)Скачать

Решение системы уравнений методом обратной матрицы - bezbotvyСкачать