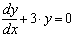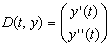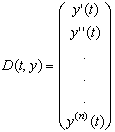Система дифференциальных уравнений второго порядка mathcad (4 видео)

Система дифференциальных уравнений второго порядка mathcad

Электронный курс по MathCAD

Содержание

5.2 Решение дифференциальных уравнений и систем.(Задача Коши и граничные задачи).
Решение одиночного дифференциального уравнения.
Численное решение задачи Коши для дифференциальных уравнений и систем.
Решение граничных задач для обыкновенных дифференциальных уравнений.
28. Тема 7. Решение дифференциальных уравнений и систем в MathCad. Краткие теоретические сведения
Система дифференциальных уравнений второго порядка mathcad
📹 Видео

5.2 Решение дифференциальных уравнений и систем.(Задача Коши и граничные задачи).

Решение одиночного дифференциального уравнения.

Для численного решения одиночного дифференциального уравнения в MathCAD имеется функция Odesolve, с помощью которой может быть решена как задача Коши для обыкновенного дифференциального уравнения, так и граничная задача. Эта функция входит в состав блока решения и сявляется его заключительным ключевым словом.

Odesolve(x,b,[step]) — Возвращает функцию, которая является решением дифференциального уравнения. Используется в блоке с оператором Given.
x — переменная интегрирования, действительное число
b — конечная точка отрезка интегрирования
step — величина шага по переменной интегрирования (необязательный аргумент)

Замечания:

Уравнение должно быть линейным относительно старшей производной.
Число заданных начальных или граничных условий внутри блока должно быть равно порядку уравнения.
При записи уравнения для обозначения производных функции используйте специальные кнопки с панели Math или ‘ (штрих) — [Ctrl+F7], для знака равенства = [Ctrl+=] (в том числе и для дополнительных условий).
Конечная точка должна быть больше начальной.
Не допускаются начальные и граничные условия смешанного типа (f ‘(a)+f(a)=5).
Искомая функция в блоке дложна быть обязательно с аргументом ( f(x))

Система дифференциальных уравнений второго порядка mathcad

Численное решение задачи Коши для дифференциальных уравнений и систем.

Для численного решения задачи Коши для дифференциальных уравнений и систем могут быть использованы функции:

rkfixed(y,x1,x2,n,F) — возвращает матрицу решений системы уравнений методом Рунге-Кутта 4-го порядка при фиксированном шаге по x

rkadapt(y,x1,x2,n,F) — ищет решение с переменным шагом ( там, где решение меняется медленнее, шаг увеличивается, а в области быстрого изменения решения шаг функции уменьшается). Возвращается решение с равным шагом. Функция работает быстрее, чем rkfixed

Bulstoer(y,x1,x2,n,F) — дает более точное решение (методом Bulirsch-Stoer)

Агрумкнты вышеуказанных функций:
y — вектор начальных условий
x1,x2 — границы интервала для поиска решения
n — количество точек на интервале
F(x,y) — вектор-функция первых производных

При решении дифференциальных уравнений порядка выше первого (или систем уравнений, выше первого порядка) исходное уравнение (систему) необходимо преобразовать к системе дифференциальных уравнений первого порядка.

В результате работы укзанных функций рассчитывается матрица, количество стобцов которой равно порядку уравнения +1(или сумме порядков уравнений в системе +1), а количество строк равно параметру n. Первый столбец содержит значения независимой переменной, второй — значение функции, третий — для диф. уравнений 2-го порядка — значение производной искомой функции (если решается система двух уравнений 1-го порядка, то третий столбец будет содержать значения второй функции). Для выделения решений (функций или их производных) можно воспользоваться стандартным оператором вывода столбцов матрицы M &lt &gt

Если матрица правых частей дифференциальных уравнений почти вырождена, то такие системы называются жесткими. В этом случае решения, возвращаемые функцией rkfixed будет неустойчивым и для решения таких систем необходимо применять функции Stiffb , Stiffr

Stiffb(y,x1,x2,n,F,J) — ищет решение диф. уравнения или системы дифференциальных уравнений методом Bulirsch-Stoer

Stiffr(y,x1,x2,n,F,J) — ищет решение диф. уравнения или системы дифференциальных уравнений методом Rosenbrock

Первые пять аргументов такие же,как и при решении хорошо обусловленных систем дифференциальных уравнений . Дополнительный аргумент — матрица J размером nx(n+1), первый столбец которой содержит частные производные dF/dx, остальные столбцы и строки представляют собой матрицу Якоби dF/dy

Пример решения жесткой системы дифференциальных уравнений.

Для отыскания решения системы диф. уравнений только в конечной точке используются функции bulstoer,rkadapt, stiffb, stiffr (начинаются с прописной буквы).

Набор парамтров для этих функций :
bulstoer(y,x1,x2,acc,F,kmax,save)
rkadapt(y,x1,x2,acc,F,kmax,save)
stiffb(y,x1,x2,acc,F,J,kmax,save)
stiffr(y,x1,x2,acc,F,J,kmax,save)

Первые три параметра и пятый (F) этих функций те же, что идля функции Rkadapt. Дополнительные параметры:
acc — параметр, контролирующий точность решения (реком. асс=0.001)
kmax — максимальное число промежуточных точек в которых ищется решение
save — минимально допустимый интервал между точками, в которых ищется решение

Решение граничных задач для обыкновенных дифференциальных уравнений.

Если для дифференциального уравнения n-го порядка k граничных условий заданы в начальной точке х1, а (n-k) граничных условий — в конечной точке х2, то такая задача называется краевой. В MathCAD реализованы две функции, позволяющие численно найти недостающие условия в точках х1 и х2.

Двухточечная краевая задача

Задача решается в два этапа. Сначала с помощью функции sbval находятся недостающие начальные значения, а затем применяется одна из выше описанных функций для решения стандартной задачи Коши на отрезке.

sbval(v,x1,x2,F,load,score) — ищет недостающие начальные условия в точке х1
v — вектор началных приближений для искомых начальных значений в точке х1,
х1,х2 — граничные точки интервала
F(x,y) — вектор-столбец из n элементов, содержит правые части дифференциальных уравнений
load(x1,v) — вектор-столбец из n элементов, содержит начальные значения в точке х1; некоторые из значений- константы, другие неизвестны и будут найдены в процессе решения.
score(x2,y) — вектор-столбец размерности вектора v, содержащий разность между начальным условием в точке х2 и значеием искомого решения в этой точке.

Краевая задача с условиями внутри интервала.

На первом этапе используется функция

balfit(V1,V2,x1,x2,xf,F,load1,load2,score) — ищет недостающие начальные условия в точках х1 и х2, сшивая решения, выходящие из этих точек, в точке xf
V1,V2 — вектора началных приближений для искомых начальных значений в точках х1 и х2
х1,х2 — граничные точки интервала
load1(x1,V1) — вектор-столбец из n элементов, содержит начальные значения в точке х1; некоторые из значений- константы, другие неизвестны и будут найдены в процессе решения
load2(x2,V2) — вектор-столбец из n элементов, содержит начальные значения в точке х2; некоторые из значений- константы, другие неизвестны и будут найдены в процессе решения.
score(xf,y) — вектор-столбец размерности n, содержащий разность между решениями, начинающимися в точках х1 и х2, в точке xf

Видео:6 Обыкновенные дифференциальные уравнения MathcadСкачать

28. Тема 7. Решение дифференциальных уравнений и систем в MathCad. Краткие теоретические сведения

Для решения дифференциальных уравнений с начальными условиями система Mathcad имеет ряд встроенных функций:

Rkfixed – функция для решения ОДУ и систем ОДУ методом Рунге–Кутта четвертого порядка с постоянным шагом;

Rkadapt – функция решения ОДУ и систем ОДУ методом Рунге–Кутта с переменным шагом;

Odesolve – функция, решающая ОДУ блочным методом.

Ниже приведено описание стандартной функции Rkfixed с указанием параметров функции.

Y – вектор начальных условий из K элементов (k – количество уравнений в системе);

X1 и X2 – левая и правая границы интервала, на котором ищется решение ОДУ или системы ОДУ;

P – число точек внутри интервала (x1, x2), в которых ищется решение;

D – вектор, состоящий из K-Элементов, который содержит первую производную искомой функции или первые производные искомых функций, если речь идет о решении системы.

Результатом работы функции является матрица из p+1 строк, первый столбец которой содержит точки, в которых получено решение, а остальные столбцы – сами решения.

На рисунке 2.7.1 приведены конкретные примеры решения различных дифференциальных уравнений и систем ОДУ в MathCAD.

При решении дифференциального уравнения первого порядка нужно создать вектор начальных условий из одного элемента Y1, который затем используется при формировании вектора-функции правой части дифференциального уравнения. При обращении к функции Rkfixed Указывается имя вектора Y, границы интервала, на котором ищется решение уравнения, например, (0 ; 2), количество точек, в которых ищется решение – 100, вектор-функция, описывающая правую часть дифференциального уравнения – D. В результате получается матрица Z, в первом столбце которой содержатся значения аргумента искомой функции, во втором – значения самой результирующей функции. При построении графика функции первый столбец полученной матрицы указывается как аргумент, второй столбец – как функция.

При решении системы дифференциальных уравнений нужно создать вектор начальных условий из двух элементов, например, вектор V, который затем используется при формировании вектора-функции правой части дифференциального уравнения. При обращении к функции Rkfixed Указывается имя вектора V, и границы интервала, на котором ищется решение уравнения, например, (0 ; 5), количество точек, в которых ищется решение – 100, вектор-функция, описывающая правую часть дифференциального уравнения – D. В результате получается матрица S, в первом столбце которой содержатся значения аргумента искомых функций, во втором и третьем столбцах – значения самих функций при соответствующем значении аргумента. При построении графика можно воспользоваться первым столбцом полученной матрицы как аргументом, а вторым и третьим столбцами – как функциями.

На рисунке 2.7.2 приведен пример решения дифференциального уравнения второго порядка с использованием функции Rkfixed. Необходимо решить дифференциальное уравнение второго порядка с заданными начальными условиями вида:

Рисунок 2.7.2 – Пример решения дифференциальных уравнений второго порядка с помощью Rkfixed

Для решения уравнения с помощью функции Rkfixed нужно выполнить замену переменных и привести дифференциальное уравнение второго порядка к двум дифференциальным уравнениям первого порядка. Вид этих уравнений приведен ниже.

Документ формируется точно так же, как и при решении системы ОДУ.

На рисунке 2.7.2 показана возможность вычисления вектора второй производной найденной функции – вектора А, построены графики исходной функции, функций первой и второй производных.

Видео:Решение дифференциальных уравнений. Решение задачи Коши. Урок 45Скачать

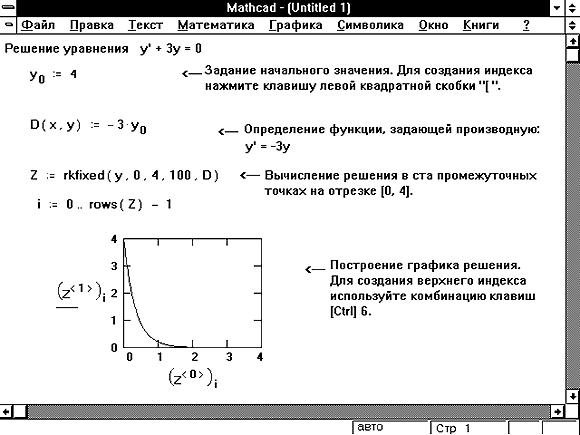
Система дифференциальных уравнений второго порядка mathcad

При решении дифференциального уравнения искомой величиной является функция. Для ОДУ неизвестная функция — функция одной переменной. Дифференциальные уравнения в частных производных — это дифференциальные уравнения, в которых неизвестной является функция двух или большего числа переменных. Mathcad имеет ряд встроенных функций, предназначенных для решения ОДУ. Каждая из этих функций предназначена для численного решения дифференциального уравнения. В результате решения получается матрица, содержащая значения функции, вычисленные на некотором множестве точек (на некоторой сетке значений). Для каждого алгоритма, который используется при решении дифференциальных уравнений, Mathcad имеет различные встроенные функции. Несмотря на различные методы поиска решения, каждая из этих функций требует, чтобы были заданы по крайней мере следующие величины, необходимые для поиска решения:

Начальные условия.
Набор точек, в которых нужно найти решение.
Само дифференциальное уравнение, записанное в некотором специальном виде, который будет детально описан в этой главе.

В этом разделе описано, как решить ОДУ, используя функцию rkfixed. Раздел начинается с примера того, как решить простейшее дифференциальное уравнение первого порядка. Затем будет показано, как можно решать дифференциальные уравнения более высокого порядка.

Дифференциальные уравнения первого порядка

Дифференциальное уравнение первого порядка — это уравнение, которое не содержит производных выше первого порядка от неизвестной функции. На Рисунке 1 показан пример того, как решить относительно простое дифференциальное уравнение:

с начальными условиями: y(0) = 4

Функция rkfixed на Рисунке 1 использует для поиска решения метод Рунге-Кутты четвертого порядка. В результате решения получается матрица, имеющая два следующих столбца:

Первый столбец содержит точки, в которых ищется решение дифференциального уравнения.
Второй столбец содержит значения найденного решения в соответствующих точках.

Рисунок 1: Решение дифференциального уравнения первого порядка.

Функция rkfixed имеет следующие аргументы:

y =	Вектор начальных условий размерности n, где n — порядок дифференциального уравнения или число уравнений в системе (если решается система уравнений). Для дифференциального уравнения первого порядка, как, например, для уравнения, приведенного на Рисунке 1, вектор начальных значений вырождается в одну точку y₀ = y(x1).
x1, x2 =	Граничные точки интервала, на котором ищется решение дифференциальных уравнений. Начальные условия, заданные в векторе y, — это значение решения в точке x1.
npoints =	Число точек (не считая начальной точки), в которых ищется приближенное решение. При помощи этого аргумента определяется число строк (1 + npoints) в матрице, возвращаемой функцией rkfixed.
D (x, y) =	Функция, возвращающая значение в виде вектора из n элементов, содержащих первые производные неизвестных функций.

Наиболее трудная часть решения дифференциального уравнения состоит в определении функции D(x, y), которая содержит вектор первых производных от неизвестных функций. В примере, приведенном на Рисунке 1, было достаточно просто разрешить уравнение относительно первой производной , и определить функцию D(x, y). Иногда, особенно в случае нелинейных дифференциальных уравнений, это может быть трудно. В таких случаях иногда удаётся разрешить уравнение относительно в символьном виде и подставить это решение в определение для функции D(x, y). Используйте для этого команду Решить относительно переменной из меню Символика.

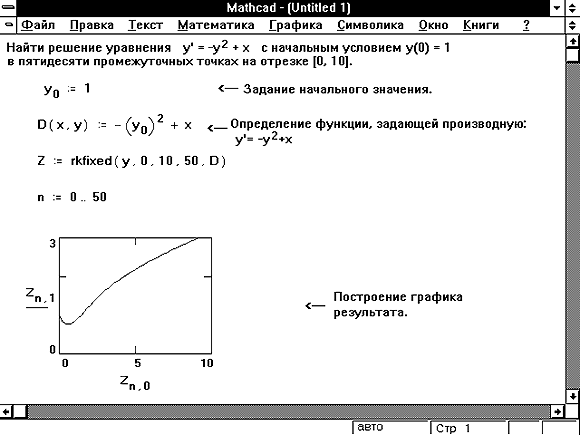
Рисунок 2: Более сложный пример, содержащий нелинейное дифференциальное уравнение.

Дифференциальные уравнения второго порядка

Как только Вы научились решать дифференциальное уравнение первого порядка, можно приступать к решению дифференциальных уравнений более высокого порядка. Мы начнем с дифференциального уравнения второго порядка. Основные отличия от уравнения первого порядка состоят в следующем:

Вектор начальных условий y теперь состоит из двух элементов: значений функции и её первой производной в начальной точке интервала x1.
Функция D(t, y) является теперь вектором с двумя элементами:

Матрица, полученная в результате решения, содержит теперь три столбца: первый столбец содержит значения t, в которых ищется решение; второй столбец содержит y(t); и третий — y‘(t).

Пример, приведенный на Рисунке 3, показывает, как решить следующее дифференциальное уравнение второго порядка:

Рисунок 3: Решение дифференциального уравнения второго порядка.

Уравнения более высокого порядка

Методика решения дифференциальных уравнений более высокого порядка является развитием методики, которая применялась для решения дифференциальных уравнений второго порядка. Основное различие состоит в следующем:

Вектор начальных значений y теперь состоит из n элементов, определяющих начальные условия для искомой функции и ее производных y, y’ , y». y (n-1)
Функция D является теперь вектором, содержащим n элементов:

Матрица, получаемая в результате решения, содержит теперь n столбцов: первый — для значений t, и оставшиеся столбцы — для значений y (t), y’ (t), y»(t). y (n-1) (t).

Пример, приведенный на Рисунке 4, показывает, как решить следующее дифференциальное уравнение четвертого порядка:

с начальными условиями: