Система дифференциальных уравнений по законам кирхгофа (3 видео)

Содержание

№74 Расчет переходных процессов методом переменных состояния.
Система дифференциальных уравнений по законам кирхгофа
Помощь с отчетом по практике
📺 Видео

Видео:Как составить уравнения по законам Кирхгофа?Скачать

№74 Расчет переходных процессов методом переменных состояния.

Уравнениями состояния электрической цепи называют любую систему дифференциальных уравнений, которая описывает состояние (режим) данной цепи. Например, система уравнений Кирхгофа является уравнениями состояния цепи, для которой она составлена.

В более узком смысле в математике уравнениями состояния называют систему дифференциальных уравнений 1-го порядка, разрешенных относительно производных (форма Коши). Система уравнений состояния в обобщенной форме имеет вид:

Та же система уравнений в матричной форме:

или в обобщённой матричной форме:

Система уравнений состояния формы Коши решается методом численного интегрирования (метод Эйлера или метод Рунге-Кутта) на ЭВМ по стандартной программе, которая должна быть в пакете стандартных программ. При отсутствии такой программы в пакете она легко может быть составлена по следующему алгоритму (метод Эйлера) для к-го шага:

Значения производных на к-ом шаге:

Значения переменных на к-ом шаге:

Для определения значений переменных и их производных на 1-м шаге ин¬тегрирова¬ния используются их значения на момент t=0, т.е. их начальные условия x1(0), x2(0). xn(0).

Уравнения состояния формы Коши для заданной схемы могут быть получены из системы уравнений Кирхгофа путем их преобразования. Для этой цели: а) из системы уравнений Кирхгофа методом подстановки исключаются »лишние» переменные, имеющие зависимые начальные условия, и оставляют переменные iL(t) и uC(t), которые не изменяются скачком и имеют независи-мые начальные условия iL(0) и uC(0); б) оставшиеся уравнения решаются относительно производных и приводятся их к форме Коши.

В случае сложных схем уравнения состояния формы Коши могут быть составлены топологическими методами с использованием матриц соединений [A] и [B].

Последовательность расчета переходного процесса методом переменных состояния выглядит так:

1. Производится расчет схемы в установившемся режиме до коммутации и определяются независимые начальные условия iL(0) и uC(0).

2. Составляется система дифференциальных уравнений по законам Кирхгофа для схемы после коммутации.

3. Методом исключения »лишних» переменных система уравнений Кирхгофа преобразуется в систему уравнений Коши, составляются матрицы коэффициентов.

4. Выбирается расчетное время (продолжительность переходного процесса) и число шагов интегрирования N.

5. Решение задачи выполняется на ЭВМ по стандартной программе. Выходную функцию получают в виде графической диаграммы x=f(t)или в виде таблицы координат функций для заданных моментов времени.

Пример. Для схемы рис. 74.1 с заданными параметрами элементов (e(t)=Emsin(ωt+ψE), R, R1, R2, R3, L1, L2, C) выполнить расчет переходного процесса и определить функцию uab(t).

1. Выполняется расчет схемы в установившемся режиме переменного тока до коммутации и определяются начальные условия i1(0), i2(0), uC(0).

2. Составляется система дифференциальных уравнений по законам Кирхгофа:

3. Система уравнений Кирхгофа преобразуется в систему уравнений Коши.

Для этой цели из (1) выражаем

и делаем подстановку в (1) и (2), а из (4) делаем подстановку в (1). Тогда получим:

Подсчитаем значения отднльных коэфициэнтов:

Составляем матрицы коэффициентов:

В качества исследуемого промежутка времени выбираем период переменного тока

Число шагов интегрирования принимаем N = 1000,

Вводим исходные данные в ЭВМ и выполняем рассчет.

В качестве выходной функции принимаем:

Для выходной функции Uab(T) строим графическую диаграмму в интервале периода Т.

Видео:Расчет переходного процесса через ДИФФЕРЕНЦИАЛЬНОЕ уравнение по законам Кирхгофа│Классический методСкачать

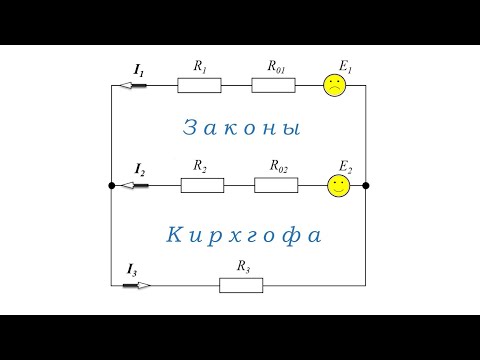
Система дифференциальных уравнений по законам кирхгофа

При всех изменениях в электрической цепи: включении, выключении, коротком замыкании, колебаниях величины какого-либо параметра и т.п. – в ней возникают переходные процессы, которые не могут протекать мгновенно, так как невозможно мгновенное изменение энергии, запасенной в электромагнитном поле цепи. Таким образом, переходный процесс обусловлен несоответствием величины запасенной энергии в магнитном поле катушки и электрическом поле конденсатора ее значению для нового состояния цепи.

При переходных процессах могут возникать большие перенапряжения, сверхтоки, электромагнитные колебания, которые могут нарушить работу устройства вплоть до выхода его из строя. С другой стороны, переходные процессы находят полезное практическое применение, например, в различного рода электронных генераторах. Все это обусловливает необходимость изучения методов анализа нестационарных режимов работы цепи.

Основные методы анализа переходных процессов в линейных цепях:

Классический метод, заключающийся в непосредственном интегрировании дифференциальных уравнений, описывающих электромагнитное состояние цепи.
Операторный метод, заключающийся в решении системы алгебраических уравнений относительно изображений искомых переменных с последующим переходом от найденных изображений к оригиналам.
Частотный метод, основанный на преобразовании Фурье и находящий широкое применение при решении задач синтеза.
Метод расчета с помощью интеграла Дюамеля, используемый при сложной форме кривой возмущающего воздействия.
Метод переменных состояния, представляющий собой упорядоченный способ определения электромагнитного состояния цепи на основе решения системы дифференциальных уравнений первого прядка, записанных в нормальной форме (форме Коши).

Классический метод расчета

Классический метод расчета переходных процессов заключается в непосредственном интегрировании дифференциальных уравнений, описывающих изменения токов и напряжений на участках цепи в переходном процессе.

В общем случае при использовании классического метода расчета составляются уравнения электромагнитного состояния цепи по законам Ома и Кирхгофа для мгновенных значений напряжений и токов, связанных между собой на отдельных элементах цепи соотношениями, приведенными в табл. 1.

Таблица 1. Связь мгновенных значений напряжений и токов на элементах электрической цепи

;

при наличии магнитной связи с катушкой, обтекаемой током ,

;

Для последовательной цепи, содержащей линейные резистор R, катушку индуктивности L и конденсатор С, при ее подключении к источнику с напряжением u (см. рис. 1) можно записать

Резистор (идеальное активное сопротивление)

Катушка индуктивности (идеальная индуктивность)

Конденсатор (идеальная емкость)

Система дифференциальных уравнений по законам кирхгофа

(1)

Подставив в (1) значение тока через конденсатор

получим линейное дифференциальное уравнение второго порядка относительно

В общем случае уравнение, описывающее переходный процесс в цепи с n независимыми накопителями энергии, имеет вид:

(2)

где х – искомая функция времени (напряжение, ток, потокосцепление и т.п.); — известное возмущающее воздействие (напряжение и (или) ток источника электрической энергии); — к-й постоянный коэффициент, определяемый параметрами цепи.

Порядок данного уравнения равен числу независимых накопителей энергии в цепи, под которыми понимаются катушки индуктивности и конденсаторы в упрощенной схеме, получаемой из исходной путем объединения индуктивностей и соответственно емкостей элементов, соединения между которыми являются последовательными или параллельными.

В общем случае порядок дифференциального уравнения определяется соотношением

(3)

где и — соответственно число катушек индуктивности и конденсаторов после указанного упрощения исходной схемы; — число узлов, в которых сходятся только ветви, содержащие катушки индуктивности (в соответствии с первым законом Кирхгофа ток через любую катушку индуктивности в этом случае определяется токами через остальные катушки); — число контуров схемы, ветви которых содержат только конденсаторы (в соответствии со вторым законом Кирхгофа напряжение на любом из конденсаторов в этом случае определяется напряжениями на других).

Наличие индуктивных связей на порядок дифференциального уравнения не влияет.

Как известно из математики, общее решение уравнения (2) представляет собой сумму частного решения исходного неоднородного уравнения и общего решения однородного уравнения, получаемого из исходного путем приравнивания его левой части к нулю. Поскольку с математической стороны не накладывается каких-либо ограничений на выбор частного решения (2), применительно к электротехнике в качестве последнего удобно принять решение , соответствующее искомой переменной х в установившемся послекоммутационном режиме (теоретически для ).

Частное решение уравнения (2) определяется видом функции , стоящей в его правой части, и поэтому называется принужденной составляющей. Для цепей с заданными постоянными или периодическими напряжениями (токами) источников принужденная составляющая определяется путем расчета стационарного режима работы схемы после коммутации любым из рассмотренных ранее методов расчета линейных электрических цепей.

Вторая составляющая общего решения х уравнения (2) – решение (2) с нулевой правой частью – соответствует режиму, когда внешние (принуждающие) силы (источники энергии) на цепь непосредственно не воздействуют. Влияние источников проявляется здесь через энергию, запасенную в полях катушек индуктивности и конденсаторов. Данный режим работы схемы называется свободным, а переменная — свободной составляющей.

В соответствии с вышесказанным, общее решение уравнения (2) имеет вид

(4)

Соотношение (4) показывает, что при классическом методе расчета послекоммутационный процесс рассматривается как наложение друг на друга двух режимов – принужденного, наступающего как бы сразу после коммутации, и свободного, имеющего место только в течение переходного процесса.

Необходимо подчеркнуть, что, поскольку принцип наложения справедлив только для линейных систем, метод решения, основанный на указанном разложении искомой переменной х, справедлив только для линейных цепей.

Начальные условия. Законы коммутации

В соответствии с определением свободной составляющей в ее выражении имеют место постоянные интегрирования , число которых равно порядку дифференциального уравнения. Постоянные интегрирования находятся из начальных условий, которые принято делить на независимые и зависимые. К независимым начальным условиям относятся потокосцепление (ток) для катушки индуктивности и заряд (напряжение) на конденсаторе в момент времени (момент коммутации). Независимые начальные условия определяются на основании законов коммутации (см. табл. 2).

Таблица 2. Законы коммутации

Первый закон коммутации (закон сохранения потокосцепления)

Магнитный поток, сцепленный с катушками индуктивности контура, в момент коммутации сохраняет то значение, которое имел до коммутации, и начинает изменяться именно с этого значения: .

Второй закон коммутации (закон сохранения заряда)

Электрический заряд на конденсаторах, присоединенных к любому узлу, в момент коммутации сохраняет то значение, которое имел до коммутации, и начинает изменяться именно с этого значения: .

Доказать законы коммутации можно от противного: если допустить обратное, то получаются бесконечно большие значения и , что приводит к нарушению законов Кирхгофа.

На практике, за исключением особых случаев (некорректные коммутации), допустимо использование указанных законов в другой формулировке, а именно:

первый закон коммутации – в ветви с катушкой индуктивности ток в момент

коммутации сохраняет свое докоммутационное значение и в дальнейшем начинает изменяться с него: .

второй закон коммутации – напряжение на конденсаторе в момент

коммутации сохраняет свое докоммутационное значение и в дальнейшем начинает изменяться с него: .

Необходимо подчеркнуть, что более общей формулировкой законов коммутации является положение о невозможности скачкообразного изменения в момент коммутации для схем с катушкой индуктивности – потокосцеплений, а для схем с конденсаторами – зарядов на них. В качестве иллюстрации сказанному могут служить схемы на рис. 2, переходные процессы в которых относятся к так называемым некорректным коммутациям (название произошло от пренебрежения в подобных схемах малыми параметрами, корректный учет которых может привести к существенному усложнению задачи).

Действительно, при переводе в схеме на рис. 2,а ключа из положения 1 в положение 2 трактование второго закона коммутации как невозможность скачкообразного изменения напряжения на конденсаторе приводит к невыполнению второго закона Кирхгофа . Аналогично при размыкании ключа в схеме на рис. 2,б трактование первого закона коммутации как невозможность скачкообразного изменения тока через катушку индуктивности приводит к невыполнению первого закона Кирхгофа . Для данных схем, исходя из сохранения заряда и соответственно потокосцепления, можно записать:

Зависимыми начальными условиями называются значения остальных токов и напряжений, а также производных от искомой функции в момент коммутации, определяемые по независимым начальным условиям при помощи уравнений, составляемых по законам Кирхгофа для . Необходимое число начальных условий равно числу постоянных интегрирования. Поскольку уравнение вида (2) рационально записывать для переменной, начальное значение которой относится к независимым начальным условиям, задача нахождения начальных условий обычно сводится к нахождению значений этой переменной и ее производных до (n-1) порядка включительно при .

Пример. Определить токи и производные и в момент коммутации в схеме на рис. 3, если до коммутации конденсатор был не заряжен.

В соответствии с законами коммутации

и .

На основании второго закона Кирхгофа для момента коммутации имеет место

и .

Для известных значений и из уравнения

определяется .

Значение производной от напряжения на конденсаторе в момент коммутации (см. табл. 1)

Корни характеристического уравнения. Постоянная времени

Выражение свободной составляющей общего решения х дифференциального уравнения (2) определяется видом корней характеристического уравнения (см. табл. 3).

Таблица 3. Выражения свободных составляющих общего решения

Вид корней характеристического уравнения

Выражение свободной составляющей

Корни вещественные и различные

Корни вещественные и

Пары комплексно-сопряженных корней

Необходимо помнить, что, поскольку в линейной цепи с течением времени свободная составляющая затухает, вещественные части корней характеристического уравнения не могут быть положительными.

При вещественных корнях монотонно затухает, и имеет место апериодический переходный процесс. Наличие пары комплексно сопряженных корней обусловливает появление затухающих синусоидальных колебаний (колебательный переходный процесс).

Поскольку физически колебательный процесс связан с периодическим обменом энергией между магнитным полем катушки индуктивности и электрическим полем конденсатора, комплексно-сопряженные корни могут иметь место только для цепей, содержащих оба типа накопителей. Быстроту затухания колебаний принято характеризовать отношением

которое называется декрементом колебания, или натуральным логарифмом этого отношения

называемым логарифмическим декрементом колебания, где .

Важной характеристикой при исследовании переходных процессов является постоянная времени t , определяемая для цепей первого порядка, как:

где р – корень характеристического уравнения.

Постоянную времени можно интерпретировать как временной интервал, в течение которого свободная составляющая уменьшится в е раз по сравнению со своим начальным значением. Теоретически переходный процесс длится бесконечно долго. Однако на практике считается, что он заканчивается при

Основы теории цепей: Учеб. для вузов /Г.В.Зевеке, П.А.Ионкин, А.В.Нетушил, С.В.Страхов. –5-е изд., перераб. –М.: Энергоатомиздат, 1989. -528с.
Бессонов Л.А. Теоретические основы электротехники: Электрические цепи. Учеб. для студентов электротехнических, энергетических и приборостроительных специальностей вузов. –7-е изд., перераб. и доп. –М.: Высш. шк., 1978. –528с.
Теоретические основы электротехники. Учеб. для вузов. В трех т. Под общ. ред. К.М.Поливанова. Т.1. К.М.Поливанов. Линейные электрические цепи с сосредоточенными постоянными. –М.: Энергия- 1972. –240с.

Видео:Урок 4. Расчет цепей постоянного тока. Законы КирхгофаСкачать

Помощь с отчетом по практике

Методы составления характеристического уравнения

Свободный режим схемы не зависит от источников энергии, определяется только структурой схемы и параметрами ее элементов. Из этого следует, что корни характеристического уравнения p1, p2,…, pn будут одинаковыми для всех переменных функций (токов и напряжений).

Характеристическое уравнение можно составить различными методами. Первый метод – классический, когда характеристическое уравнение составляется строго в соответствии с дифференциальным по классической схеме. При расчете переходных процессов в сложной схеме составляется система из “m” дифференциальных уравнений по законам Кирхгофа для схемы цепи после коммутации. Так как корни характеристического уравнения являются общими для всех переменных, то решение системы дифференциальных уравнений выполняется относительно любой переменной (по выбору). В результате решения получают неоднородное дифференциальное уравнение с одной переменной. Составляют характеристическое уравнение в соответствии с полученным дифференциальным и определяют его корни.

Пример. Составить характеристическое уравнение и определить его корни для переменных в схеме рис. 131. Параметры элементов заданы в общем виде. Закон сохранения заряда

Система дифференциальных уравнений по законам Кирхгофа:

Решим систему уравнений относительно переменной i3, в результате получим неоднородное дифференциальное уравнение:

Характеристическое уравнение и его корень:

Второй способ составления характеристического уравнения заключается в приравнивании нулю главного определителя системы уравнений Кирхгофа для свободных составляющих переменных.

Пусть свободная составляющая произвольного тока имеет вид , тогда

Система уравнений для свободных составляющих получается из системы дифференциальных уравнений Кирхгофа путем замены производных от переменных на множитель р, а интегралов – на 1/р. Для рассматриваемого примера система уравнений для свободных составляющих имеет вид:

Характеристическое уравнение и его корень:

Третий способ составления характеристического уравнения (инженерный) заключается в приравнивании нулю входного операторного сопротивления схемы относительно любой ее ветви.

Операторное сопротивление элемента получается из его комплексного сопротивления путем простой замены множителя jω на р, следовательно

Для рассматриваемого примера:

Третий способ является наиболее простым и экономичным, поэтому он чаще других применяется при расчете переходных процессов в электрических цепях.

Корни характеристического уравнения характеризуют свободный переходной процесс в схеме без источников энергии. Такой процесс протекает с потерями энергии и поэтому затухает во времени. Из этого следует, что корни характеристического уравнения должны быть отрицательными или иметь отрицательную вещественную часть.

В общем случае порядок дифференциального уравнения, которым описывается переходный процесс в схеме, и, следовательно, степень характеристического уравнения и число его корней равны числу независимых начальных условий, или числу независимых накопителей энергии (катушек L и конденсаторов C). Если в схеме цепи содержатся параллельно включенные конденсаторы С1, С2,… или последовательно включенные катушки L1, L2,…, то при расчете переходных процессов они должны быть заменены одним эквивалентным элементом СЭ =С1 +С2+… или LЭ =L1 +L2+…

Таким образом, общий вид решения для любой переменной при расчете переходного процесса может быть составлен только из анализа схемы цепи, без составления и решения системы дифференциальных уравнений.

Для рассматриваемого выше примера:

а) – при e(t)=E=const;

б) – при e(t)=Emsin(ωt+ ).

7. Определение постоянных интегрирования

Определение постоянных интегрирования производится на заключительном этапе расчета переходного процесса, когда остальные составляющие решения уже найдены. Постоянные интегрирования определяются путем подстановки в решение для искомой функции соответствующих начальных условий.

Пусть решение для искомой функции i(t) содержит только одну постоянную интегрирования:

Постоянная интегрирования находится путем подстановки в решение начального условия для самой функции, т.е. i(0):

Пусть решение для искомой функции i(t) содержит две постоянных интегрирования и имеет вид:

Постоянные интегрирования в этом случае находятся путем подстановки в решение начальных условий для самой функции i(0) и для ее первой производной :

В результате совместного решения этой системы уравнений определяют искомые постоянные интегрирования А1 и А2 .

Последовательность выполнения отдельных этапов расчета переходных процессов классическим методом показана ниже в виде диаграммы.

Примечания: 1. Выполнение всех этапов, обозначенных в диаграмме клетками, является обязательным и необходимым.

Выполнение первых пяти этапов, находящихся в верхнем горизонтальном ряду диаграммы, может производиться в любой последовательности, так как они не зависят друг от друга.

Пример. Для схемы рис. 132 с заданными параметрами элементов: Е=100 В, R=50 Ом, R1=20 Ом, R2=30 Ом, С=83,5 мкФ, определить ток i1 после коммутации.

1)Общий вид решения для искомой функции:

2)Определение установившейся составляющей из расчета схемы после коммутации:

3)Характеристическое уравнение и его корень:

4)Независимое начальное условие uс(0) из расчета схемы до коммутации:

5)Система дифференциальных уравнений по законам Кирхгофа для схемы после коммутации:

6)Начальное условие i1(0), необходимое для определения постоянной интегрирования из уравнения (1):

7)Определение постоянной интегрирования:

8)Решение для искомой функции:

9)Графическая диаграмма искомой функции i1(t) показана на рис. 133:

9. Операторный метод расчета переходных процессов

Если система дифференциальных уравнений, которыми описывается переходной процесс в схеме, решается операционным методом, то и сам метод расчета переходного процесса также называется операционным или операторным.

Сущность операторного метода состоит в том, что на 1-ом этапе действительные функции времени i(t), u(t), называемые оригиналами, заменяются некоторыми новыми функциями I(p),U(p), называемыми операторными изображениями. Соответствие между оригиналом функции f(t) и ее операторным изображением F(p) устанавливается на основе прямого преобразования интеграла Лапласа:

где Û знак соответствия; p=+j — комплексный оператор Лапласа.

Если s  = , то p= j, и преобразование Лапласа превращается в преобразование Фурье, которое лежит в основе комплексного метода расчета цепей переменного тока.

Преобразование Лапласа позволяет заменить операции 2-го рода над оригиналами функций (дифференцирование и интегрирование) на операции 1-го рода (умножение и деление) над операторными изображениями этих функций.

Расчет переходных процессов операторным методом условно выполняется в 3 этапа.

На 1-м этапе расчета система дифференциальных уравнений, составленная по законам Кирхгофа для оригиналов функций, после применения преобразования Лапласа превращается в систему алгебраических уравнений для операторных изображений этих функций.

На 2-ом этапе выполняется решение системы алгебраических операторных уравнений относительно искомой функции, в результате чего получают выражение искомой функции в операторной форме F(p).

На заключительном 3-м этапе выполняется обратный переход от найденного операторного решения для искомой функции F(p) к соответствующей ей функции времени f(t), т. е. Выполняется переход от изображения функции F(p) к ее оригиналу f(t).

Теоретически обратный переход от операторного изображения функции F(p) к ее оригиналу f(t) устанавливается на основе обратного преобразования Лапласа:

На практике для обратного перехода используются более простые и удобные методы, а именно: формула разложения и таблицы соответствия.

10. Операторные изображения некоторых функций времени

Найдем операторные изображения некоторых функций времени, которые встречаются в электротехнике.

Изображение постоянной функции f(t)=А:

2) Изображения экспоненциальных функций:

3) Изображения гармонических функций:

Изображения 1-ой и 2-ой производной от функции времени:

Изображение определенного интеграла от функции:

Для удобства пользования сведем полученные результаты в общую таблицу, которая называется таблицей соответствия.

11. Законы электротехники в операторной форме

Мгновенные значения тока i(t) и напряжения u(t) на идеальных элементах электрических схем связаны между собой дифференциальной формой уравнений: uR(t) = iR – для резистора; — для катушки индуктивности; — для конденсатора.

Применим к дифференциальным уравнениям преобразование Лапласа и получим соответствующее им операторные изображения: — для резистора; — для катушки индуктивности; — для конденсатора.

Таким образом, идеальным элементам R, L, C электрической схемы будут соответствовать новые схемные представления этих элементов в операторной схеме (см. табл.).

Здесь R, pL, 1/pC – операторные сопротивления соответственно резистора R, катушки L и конденсатора C. Операторное сопротивление Z(p) любого участка схемы можно получить из его комплексного сопротивления Z(j w ), заменив в выражении множитель j w на оператор p.

Li(0), uC(0)/p – внутренние источники ЭДС, обусловленные запасами энергии в магнитном и электрическом полях в момент коммутации при t=0. Направления действия внутренних источников ЭДС принимаются по направлению тока i(0) для источника L i(0) и навстречу напряжению uC(0) для источника uC(0)/p.

C учетом полученных соотношений любую электрическую схему для оригиналов функций i(t), u(t) можно заменить соответствующей ей операторной схемой для изображений функций I(p) ,U(p). Например, электрической схеме рис. 134 соответствует операторная схема, представленная на рис. 135.

Для электрической схемы рис. 134 справедливо дифференциальное уравнение, составленное по 2-му закону Кирхгофа:

Для операторной схемы рис. 135 справедливо аналогичное уравнение, но в операторной форме:

где – операторное сопротивление всей схемы, — сумма всех источников ЭДС контура, в том числе и внутренних.

Для сложных операторных схем справедливы 1-й и 2-й законы Кирхгофа в операторной форме:

Для расчета таких схем можно применять любые методы расчета линейных цепей: метод законов Кирхгофа, метод контурных токов, метод узловых потенциалов и другие. Порядок составления операторных уравнений для сложных схем аналогичен методу, тому порядку, который применяется по этому методу для электрических схем.