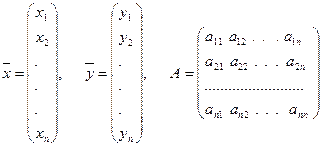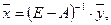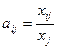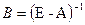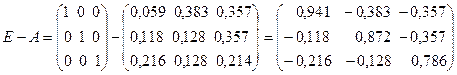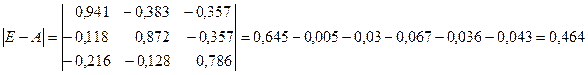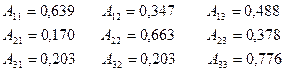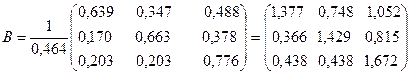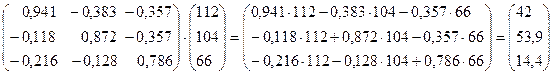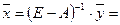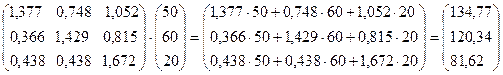Введем в рассмотрение векторы-столбцы объёмов произведенной продукции (вектор валового выпуска), объёмов продукции конечного потребления (вектор конечного потребления) и матрицу коэффициентов прямых затрат:
Тогда система уравнений (3) в матричной форме имеет вид:
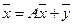
Обычно это соотношение называют уравнением линейного межотраслевого баланса.
Уравнение межотраслевого баланса можно использовать в двух целях.
В первом, наиболее простом случае, когда известен вектор валового выпуска 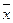
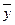
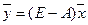
где E – единичная матрица той же размерности, что и матрица прямых затрат A.
Во втором случае уравнение межотраслевого баланса используется для целей планирования со следующей формулировкой задачи: для периода времени Т (например, год) известен вектор конечного потребления 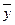
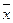
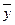
где 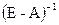
Если решение уравнения (4) существует, то матрица A называется продуктивной.
1. Матрица A продуктивна тогда и только тогда, когда матрица 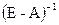
2. Матрица A с неотрицательными элементами продуктивна, если сумма элементов по любому её столбцу или строке не превосходит единицы, причем хотя бы для одного столбца или строки эта сумма строго меньше единицы.
ЗАДАЧА 1.
Таблица (1) содержит данные баланса трех отраслей промышленности за отчетный период. Требуется:
1) Убедиться, что модель продуктивна, т.е. найти матрицу коэффициентов прямых затрат и убедиться в том, что она продуктивна;
2) Составить баланс производства и распределения продукции;
3) Найти конечный продукт (вектор конечного продукта 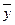
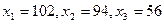
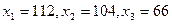
4) Найти валовой продукт (вектор валового выпуска 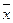
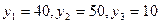
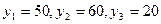
| № п.п. | Производящие отрасли | Потребляющие отрасли | Конечный продукт | Валовой продукт |
| Машиностроение | ||||
| Ракетостроение | ||||
| Нефтехимия |
Решение.
1. Найдем матрицу коэффициентов прямых затрат. Из (1)
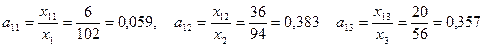
Получим следующую матрицу прямых затрат:
| Итоги | |||
| 0,059 | 0,383 | 0,357 | 0,799 |
| 0,118 | 0,128 | 0,357 | 0,603 |
| 0,216 | 0,128 | 0,214 | 0,558 |
| Итоги | 0,393 | 0,639 | 0,928 |
2. Проверка продуктивности матрицы прямых затрат. Для проверки используем второй критерий. Для этого вычисляем суммы элементов в строках и столбцах. Результаты приведены в таблице (2). Поскольку все суммы элементов и в столбцах и в строках меньше единицы, то матрица продуктивна. Исходя из этого можно утверждать, что для неё существует обратная матрица с положительными коэффициентами.
3. Составим баланс производства и распределения продукции.
Модель баланса производства и распределения продукции отрасли можно представить следующей системой уравнений:
4. Найдем матрицу полных затрат
Каждый элемент матрицы B рассчитывается по формуле 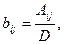
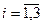
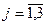
где Aij— алгебраические дополнения элементов матрицы (E-A); D- определитель матрицы (E-A).
Определитель матрицы (E-A):
Расчет алгебраических дополнений матрицы (E-A) дает следующие результаты:
Составим матрицу B:
Замечание. Поскольку матрица A продуктивна, то все коэффициенты матрицы полных затрат должны быть положительны. Отрицательные значения будут свидетельствовать об ошибке в расчетах.
5. Вычисление нового конечного продукта (вектора конечного продукта) при измененном валовом выпуске: 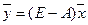

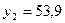
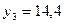
6. Вычисление нового валового продукта (вектора валового выпуска) при измененном конечном потреблении: 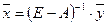
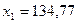
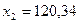
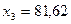
- Межотраслевые балансовые модели
- Глава 2. Межотраслевые балансовые модели.
- 2.1. Межотраслевой баланс
- 2.2. Статическая балансовая модель производства.
- Линейные балансовые модели в экономике
- Главная > Документ
- Статическая модель межотраслевого баланса. Коэффициенты прямых материальных затрат. Достаточное условие продуктивности матрицы коэффициентов прямых материальных затрат. Структурная форма линейной модели баланса межотраслевых материально-вещественных связей.
- 🌟 Видео
Видео:Модель межотраслевого баланса. Часть 1 ТеорияСкачать

Межотраслевые балансовые модели
Видео:Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

Глава 2. Межотраслевые балансовые модели.
Видео:Решение системы уравнений методом ГауссаСкачать

2.1. Межотраслевой баланс
Часто при экономическом планировании на уровне регионов или страны в целом возникает необходимость определения объема выпуска товаров, обеспечивающего заданный спрос населения и производственные нужды. Решить эту задачу можно с использованием балансовых моделей производства и распределения продукции. В. основе построения этих моделей лежит балансовый метод, т. е. метод взаимного сопоставления имеющихся материальных, трудовых и финансовых ресурсов с потребностью в них.
Балансовые методы планирования можно рассматривать на различных уровнях иерархии экономических объектов: предприятиях, объединениях, отраслях, народном хозяйстве в целом. Модель межотраслевого баланса (МОБ) исторически является первой экономико-математической моделью сводного народнохозяйственного планирования. Первые балансы народного хозяйства были разработаны Центральным статистическим управлением СССР в гг. В настоящее время межотраслевые балансы на национальном уровне составляются приблизительно в восьмидесяти странах мира. Также строятся межотраслевые балансы на уровне регионов и крупных городов
Предшественниками МОБ были: экономическая таблица Ф. Кенэ (1758) и схемы общественного воспроизводства К. Маркса (XIX в.). Русский экономист (), изучая межотраслевые связи, впервые использовал для этой цели линейные уравнения и предложил технологические коэффициенты. Автором современной модели межотраслевого баланса (в англоязычных странах он имеет название «input-output analysis») является американский ученый (русский по происхождению) Василий Леонтьев. В 1973 году за разработанные методы экономического анализа (модель “затраты–выпуск ”) ему была присуждена Нобелевская премия.
Эта модель позволяет рассчитывать полные затраты валовой продукции, прямые и косвенные затраты на единицу продукции, а также дает возможность устанавливать четкие количественные соотношения между валовым общественным продуктом, национальным доходом, развитием отдельных отраслей экономики Метод универсален. С его помощью американцы, например, проводили перестройку экономики с военных рельсов на мирные. Он был положен в основу индикативных планов, применяемых в Японии.
Межотраслевой баланс производства и распределения продукции – инструмент анализа и планирования структуры общественного производства, учитывающий комплексные взаимосвязи отраслей производственной сферы. В зависимости от того, в каких единицах измеряются потоки продуктов в балансе, существует различные варианты межотраслевых балансов: в натуральном выражении, в стоимостном, в натурально-стоимостном, в трудовых измерителях. По экономическому содержанию информации балансы можно разделить на плановые и отчетные; по характеру используемой модели – на статические и динамические.
Рассмотрим фрагмент (три раздела) отчетного межотраслевого баланса (МОБ), в котором потоки продукции измеряются на основе стоимости произведенной продукции в некоторых фиксированных ценах (табл. 1). Основу баланса составляет совокупность 
Фрагмент таблицы межотраслевого баланса



В первом разделе содержится информация о межотраслевых связях. Величины 


Таким образом, каждая 




В столбцах первого раздела баланса отражается структура материальных затрат каждой отрасли. 


Таким образом, первый раздел МБ показывает общую картину производственных затрат и распределения продукции отраслей на производственные цели. Данные I квадранта играют решающую роль в анализе структуры материальных затрат отраслей, пропорций и производственных связей между отраслями, потоков системе материально-технического снабжения.
Во втором разделе содержатся величины 


Конечный продукт – это продукция отраслей материального производства, поступающая на цели личного и общественного непроизводственного потребления, накопление и возмещение выбытия основных фондов, прирост запасов, затраты на просвещение, здравоохранение, экспорт и т. д.).


В развернутых схемах баланса конечный продукт каждой отрасли показывают дифференцировано по направлениям использования: для потребления, инвестиции, прирост запасов и резервов, экспорт и прочие расходы.
Первый и второй раздел межотраслевого баланса называют таблицей «затраты-выпуск». По строкам этой таблицы строится следующее балансовое соотношение:


т. е. валовой продукт каждой отрасли равен сумме конечного и промежуточного продуктов.
В третьем разделе МБ отражается стоимостная структура валового продукта отраслей. В нашей таблице третий раздел представлен 2-я строками. В первой стоят величины 



Добавленная стоимость — это та часть стоимости продукта, которая создается в данной отрасли, Она отражает прибыль, заработную плату, амортизационные отчисления, налоги и прочие издержки, понесенные каждым объектом (отраслью) в дополнение к платежам за ресурсы, поступившие из других отраслей.
Обычно в развернутых МБ условно-чистую продукцию подразделяют на амортизационные отчисления и чистую продукцию.
Из соотношений (2.1) и (2.2) следует

откуда получаем: 
Это соотношение показывает, что суммарный конечный продукт экономической системы (национальный доход) равен суммарной условно–чистой продукции. Таким образом, третий раздел также характеризует национальный доход, но со стороны его стоимостного состава как сумму оплаты труда и чистого дохода всех отраслей материального производства, а величины 
Данные третьего раздела необходимы для анализа соотношений между вновь созданной и перенесенной стоимостью, между величиной необходимого и прибавочного продукта в целом по материальному производству и в отраслевом разрезе. В целом же уравнение (2.4) показывает, что в межотраслевом балансе соблюдается важнейший принцип единства материально-вещественного и стоимостного состава национального дохода.
Следует отметить, что баланс в натуральных измерителях обычно содержит только показатели I и II разделов схемы межотраслевого баланса. Он разрабатывается по важнейшим видам продукции и обычно не охватывает всего общественного производства.
Подчеркнем, что рассмотренный нами отчетный МБ – это пока не модель, а лишь способ представления статистической информации об экономике страны. Он строится на основе агрегирования результатов отдельных предприятий. Кроме отчетных МБ разрабатываются плановые МБ. Для их построения необходимо использовать межотраслевые балансовые модели.
Видео:МЕТОД АЛГЕБРАИЧЕСКОГО СЛОЖЕНИЯ 😉 СИСТЕМЫ УРАВНЕНИЙ ЧАСТЬ II #математика #егэ #shorts #профильныйегэСкачать

2.2. Статическая балансовая модель производства.
Балансовая модель строится на следующих предположениях о свойствах экономического объекта:
· Экономическая система состоит из нескольких экономических объектов. Количество выпускаемой каждым объектом продукции может быть охарактеризовано одним числом, в качестве которого чаще всего рассматривается валовой выпуск в некоторых фиксированных ценах.
· Выпускаемая каждым объектом продукция частично потребляется другими объектами системы, а частично поступает вовне в качестве конечного продукта данной системы, т. е. выполняется соотношение


· Цель системы заключается в производстве заданного количества конечного продукта.
· Свойство комплектности потребления: для выпуска заданного количества продукта объект должен получать строго определенное количество других продуктов.
· Свойство линейности потребления: увеличение выпуска продукции в некоторое число раз требует увеличения потребления объектом всех других продуктов в то же самое число раз.
Очевидно, что сформулированные предположения лишь приближенно отражают реальную экономическую ситуацию, к примеру, предположение о комплектности потребления, которое предполагает, что технология производства в каждом объекте остается неизменной в течение рассматриваемого промежутка времени, причем в каждой отрасли имеется единственная технология производства, не допускается замещение одного ресурса другим.
В реальном производстве один и тот же продукт в зависимости от применяемой технологии может требовать различное количество инградиентов, а в модели предполагается, что продукт производится некоторым усредненным способом. Несмотря на эти упрощения, балансовая модель является удобным инструментом планирования благодаря своей простоте и возможности расчета всех показателей плана.
Выберем в качестве переменных модели величины валового выпуска — 





Свойства линейности и комплектности потребления определяют закономерности преобразования ресурсов в системе, а именно, согласно свойству комплектности для выпуска единицы продукции 





Матрица, составленная из величин 
A=
Из экономического смысла величин 



Видео:Решение системы линейных уравнений графическим методом. 7 класс.Скачать

Линейные балансовые модели в экономике
Главная > Документ
| Информация о документе | |
| Дата добавления: | |
| Размер: | |
| Доступные форматы для скачивания: |
Есть два основных пути.
Статистический . Коэффициенты а ij определяются на основе анализа отчетных балансов за прошлые годы. Неизменность во времени коэффициентов прямых затрат в этом случае достигается подходящим выбором отраслей межотраслевого баланса. Как показывает практика, при правильном выборе достаточно крупных отраслей коэффициенты а ij оказываются достаточно устойчивыми.
где X ij и X j взяты из отчетного баланса.
Нормативный . Строится модель отрасли межотраслевого баланса. В этой модели отрасль рассматривается как совокупность отдельных производств, для каждого из которых уже разработаны нормативы затрат. Если заранее знать, какую продукцию будут выпускать производства отрасли, то по нормативам затрат можно рассчитать среднеотраслевые коэффициенты прямых затрат.
Определив коэффициенты а ij , можно использовать систему (4) для решения сформулированных выше задач 1 – 3.
Технологические коэффициенты а ij обладают следующими свойствами:
Пример . Используя отчетный баланс:
Постройте систему балансовых уравнений.
По вектору Y = (10, 20) найдите вектор X .
Найдите вектор Y , если X = (50,100).
При Y = (10, 20) система из п.2 принимает вид:
Решая эту систему, получим:
Если X = (50,100), то из системы в п.2 получим:
IV . Решение системы балансовых уравнений в матричной форме
Систему (4) заменим матричным уравнением:
где
Система (5) позволяет по данному вектору-столбцу объемов производства найти вектор-столбец конечной продукции.
Для решения обратной задачи надо решить следующую систему:
X = ( E — A ) — 1 Y , (6)
где ( E — A ) -1 – матрица, обратная матрице ( E — A ).
Матрица А называется продуктивной , если существует неотрицательный вектор X 0 , такой, что X 0 > A X 0 . Другими словами, если матрица А продуктивна, то для выпуска продукта каждой отрасли требуется затрат меньше, чем стоит сам продукт.
Матрица А продуктивна тогда и только тогда, когда матрица B =( E — A ) -1 неотрицательна.
Матрицу В = || b ij || называют матрицей коэффициентов полных внутренних затрат . Коэффициент b ij выражает стоимость той части валового продукта P i , которая необходима P i для выпуска ею единицы конечной продукции.
До сих пор мы говорили о затратах, распределении и потреблении продукции, произведенной экономическими объектами, входящими в данную экономическую систему. Однако, если экономическая система не охватывает всю экономику страны, то не исключена возможность того, что в процессе производства в качестве сырья, полуфабрикатов и т. д. будут использоваться продукты, произведенные за ее пределами.
Особая роль принадлежит трудовым ресурсам и капиталовложениям. Эти два фактора производства всегда являются внешними по отношению к любой экономической системе. Тем не менее с помощью метода межотраслевого баланса можно определить затраты труда, капитала и других ресурсов, не производящихся внутри нее.
Статическая модель межотраслевого баланса. Коэффициенты прямых материальных затрат. Достаточное условие продуктивности матрицы коэффициентов прямых материальных затрат. Структурная форма линейной модели баланса межотраслевых материально-вещественных связей.
Межотраслевой баланс (МОБ) представляет собой таблицу, в которой отражен процесс формирования и использования совокупного общественного продукта в отраслевом разрезе.
Балансы бывают отчетные и плановые. Отчетные фиксируют сложившиеся пропорции, а плановые отражают некоторое желательное состояние и получаются в результате расчета по моделям, о которых и пойдет речь в этой главе.
В зависимости от того, в каких единицах измеряются межотраслевые потоки, различают балансы натуральные и стоимостные. Далее мы будем иметь в виду в основном стоимостные балансы.
Предположим, что народное хозяйство представлено совокупностью п отраслей. Будем считать, что каждая отрасль производит только один продукт и каждый продукт производится только одной отраслью, т. е. между отраслями и продукцией существует взаимно однозначное соответствие. В действительности это не так, поэтому в МОБ фигурируют не реальные, а так называемые «чистые», или «технологические», отрасли.
Общий вид межотраслевого баланса представлен в таблице. Она состоит из четырех разделов. Первый раздел образуется перечнем «чистых» отраслей. Каждая отрасль представлена в МОБ дважды: как производящая и как потребляющая. Отрасли как производителю соответствует строка таблицы, отрасли как потребителю соответствует столбец. На пересечении i -й строки и j -го столбца находится величина x ij — количество продукции i -й отрасли (в денежном выражении), израсходованной на производственные нужды j -й отрасли. Таким образом, первый раздел характеризует межотраслевые потоки сырья, материалов, энергии и т. д., обусловленные производственной деятельностью отраслей.
🌟 Видео
Матричный метод решения систем уравненийСкачать

Модель Леонтьева. Теория и решение задачи.Скачать

Метод Крамера за 3 минуты. Решение системы линейных уравнений - bezbotvyСкачать

Урок 4. Уравнения и системы уравнений. Алгебра ОГЭ . Вебинар | МатематикаСкачать

МЕТОД ГАУССА 😉 #егэ #математика #профильныйегэ #shorts #огэСкачать

Решение системы уравнений методом обратной матрицы - bezbotvyСкачать

Алгебра 9 класс. Графическое решение систем уравненийСкачать

Решение системы уравнений в ExcelСкачать

Считаем в уме за секунду. #математика #арифметика #счет #ментальнаяарифметика #simplemathСкачать

Математика это не ИсламСкачать

Математика | Система уравнений на желтую звездочку (feat Золотой Медалист по бегу)Скачать

ОВР и Метод Электронного Баланса — Быстрая Подготовка к ЕГЭ по ХимииСкачать

Метод Жордана-Гаусса (метод прямоугольников). ВидеоурокСкачать

Модель межотраслевого баланса. Часть 2 ПрактикаСкачать

Химия | Задачи на систему уравненийСкачать