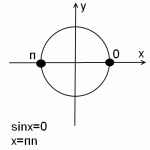Синус равен 0 на окружности уравнение

Знание — сила. Познавательная информация

Видео:Тригонометрическая окружность. Как выучить?Скачать

sinx=0

Эта ассоциация позволяет легко запомнить, где синус равен 0, и быстро решить уравнение sin x=0.

Как обычно, частные случаи синуса рассматриваем на единичной окружности.

Используем ассоциацию косинус-колобок. Оба начинаются с ко-, в названии cos x буква o тоже косвенно на колобка указывает. Колобок движется по горизонтали. На координатной плоскости движение по горизонтали происходит вдоль оси x.

Поэтому cos x — это x, соответственно, sin x — это y.

Таким образом, чтобы найти, где синус равен 0, нужно выяснить, в каких точках y=0.

Раз y=0, то движения вверх-вниз не происходит.

На единичной окружности условию sin x=0 удовлетворяют две точки: 0 и π.

Чтобы из одной точки попасть в другую, надо пройти половину окружности, то есть π.

Поскольку таких точек, в которых синус равен 0, бесконечное множество, прибавляем не π, а πn, где n — целое число (то есть n принадлежит Z): x=0+πn.

Следовательно, решение уравнения sin x=0, есть множество точек

Видео:ТЕОРЕМА СИНУСОВ И ТЕОРЕМА КОСИНУСОВ. Тригонометрия | МатематикаСкачать

Синус

Синус – одна из тригонометрических функций. Значение синуса определяется для угла или для числа (в этом случае используют числовую окружность).

Видео:ЗНАЧЕНИЯ СИНУСА И КОСИНУСА НА ОКРУЖНОСТИСкачать

Аргумент и значение

Видео:Синус, косинус, тангенс, котангенс за 5 МИНУТСкачать

Синус острого угла

Синус острого угла можно определить с помощью прямоугольного треугольника — он равен отношению противолежащего катета к гипотенузе.

1) Пусть дан угол и нужно определить синус этого угла.

2) Достроим на этом угле любой прямоугольный треугольник.

3) Измерив, нужные стороны, можем вычислить (sinA).

Видео:10 класс, 11 урок, Числовая окружностьСкачать

Синус числа

Синус числа можно определить с помощью числовой окружности – синус числа равен ординате соответствующей точки на ней.

Числовая окружность позволяет определить синус любого числа, но обычно находят синус чисел как-то связанных с Пи : (frac) , (frac) , (-2π).

Например, для числа (frac) — синус будет равен (0,5). А для числа (-) (frac) он будет равен (-) (frac<sqrt>) (приблизительно (-0,71)).

Подробнее как вычисляется синус разных чисел можно прочитать в этой статье .

Значение синуса всегда лежит в пределах от (-1) до (1). При этом вычислен он может быть для абсолютно любого угла и числа.

Видео:Простейшие тригонометрические уравнения. y=sinx. 1 часть. 10 класс.Скачать

Синус любого угла

Благодаря единичному кругу можно определять тригонометрические функции не только острого угла, но и тупого, отрицательного, и даже большего, чем (360°) (полный оборот). Как это делать — проще один раз увидеть, чем (100) раз услышать, поэтому смотрите картинку.

Теперь пояснение: пусть нужно определить (sin∠КОА) с градусной мерой в (150°). Совмещаем точку О с центром окружности, а сторону ОК – с осью (x). После этого откладываем (150°) против часовой стрелки. Тогда ордината точки А покажет нам (sin⁡∠KOA).

Если же нас интересует угол с градусной мерой, например, в (-60°) (угол КОВ), делаем также, но (60°) откладываем по часовой стрелке.

И, наконец, угол больше (360°) (угол КОС) — всё аналогично тупому, только пройдя по часовой стрелке полный оборот, отправляемся на второй круг и «добираем нехватку градусов». Конкретно в нашем случае угол (405°) отложен как (360° + 45°).

Несложно догадаться, что для откладывания угла, например, в (960°), надо сделать уже два оборота ((360°+360°+240°)), а для угла в (2640°) — целых семь.

Как вы могли заменить, и синус числа, и синус произвольного угла определяется практически одинаково. Изменяются только способ нахождения точки на окружности.

Видео:ТРИГОНОМЕТРИЯ | Синус, Косинус, Тангенс, КотангенсСкачать

Связь с другими тригонометрическими функциями:

— косинусом того же угла (или числа): основным тригонометрическим тождеством (sin^2⁡x+cos^2⁡x=1)
— тангенсом и косинусом того же угла (или числа): формулой (tg⁡x=) (frac)
— котангенсом того же угла (или числа): формулой (1+сtg^2⁡x=) (frac)
Другие наиболее часто применяемые формулы смотри здесь .

Видео:ТРИГОНОМЕТРИЯ ЗА 10 МИНУТ — Синус, Косинус, Тангенс, Котангенс // Подготовка к ЕГЭ по МатематикеСкачать

Функция (y=sin⁡x)

Если отложить по оси (x) углы в радианах, а по оси (y) — соответствующие этим углам значения синуса, мы получим следующий график:

График данной функции называется синусоида и обладает следующими свойствами:

— область определения – любое значение икса: (D(sin⁡x )=R)
— область значений – от (-1) до (1) включительно: (E(sin⁡x )=[-1;1])
— нечетная: (sin⁡(-x)=-sin⁡x)
— периодическая с периодом (2π): (sin⁡(x+2π)=sin⁡x)
— точки пересечения с осями координат:
ось абсцисс: ((πn;0)), где (n ϵ Z)
ось ординат: ((0;0))
— промежутки знакопостоянства:
функция положительна на интервалах: ((2πn;π+2πn)), где (n ϵ Z)
функция отрицательна на интервалах: ((π+2πn;2π+2πn)), где (n ϵ Z)
— промежутки возрастания и убывания:
функция возрастает на интервалах: ((-) (frac) (+2πn;) (frac) (+2πn)), где (n ϵ Z)
функция убывает на интервалах: (() (frac) (+2πn;) (frac) (+2πn)), где (n ϵ Z)
— максимумы и минимумы функции:
функция имеет максимальное значение (y=1) в точках (x=) (frac) (+2πn), где (n ϵ Z)
функция имеет минимальное значение (y=-1) в точках (x=-) (frac) (+2πn), где (n ϵ Z).

Видео:Отбор корней по окружностиСкачать

Геометрия. Урок 1. Тригонометрия

Смотрите бесплатные видео-уроки по теме “Тригонометрия” на канале Ёжику Понятно.

Видео-уроки на канале Ёжику Понятно. Подпишись!

Содержание страницы:

Видео:Решение тригонометрических уравнений. Подготовка к ЕГЭ | Математика TutorOnlineСкачать

Тригонометрия в прямоугольном треугольнике

Рассмотрим прямоугольный треугольник. Для каждого из острых углов найдем прилежащий к нему катет и противолежащий.

Синус угла – отношение противолежащего катета к гипотенузе.

sin α = Противолежащий катет гипотенуза

Косинус угла – отношение прилежащего катета к гипотенузе.

cos α = Прилежащий катет гипотенуза

Тангенс угла – отношение противолежащего катета к прилежащему (или отношение синуса к косинусу).

tg α = Противолежащий катет Прилежащий катет

Котангенс угла – отношение прилежащего катета к противолежащему (или отношение косинуса к синусу).

ctg α = Прилежащий катет Противолежащий катет

Рассмотрим прямоугольный треугольник A B C , угол C равен 90 °:

sin ∠ A = C B A B

cos ∠ A = A C A B

tg ∠ A = sin ∠ A cos ∠ A = C B A C

ctg ∠ A = cos ∠ A sin ∠ A = A C C B

sin ∠ B = A C A B

cos ∠ B = B C A B

tg ∠ B = sin ∠ B cos ∠ B = A C C B

ctg ∠ B = cos ∠ B sin ∠ B = C B A C

Видео:🔴 ТРИГОНОМЕТРИЯ С НУЛЯ (Тригонометрическая Окружность на ЕГЭ 2024 по математике)Скачать

Тригонометрия: Тригонометрический круг

Тригонометрия на окружности – это довольно интересная абстракция в математике. Если понять основной концепт так называемого “тригонометрического круга”, то вся тригонометрия будет вам подвластна. В описании к видео есть динамическая модель тригонометрического круга.

Тригонометрический круг – это окружность единичного радиуса с центром в начале координат.

Такая окружность пересекает ось х в точках ( − 1 ; 0 ) и ( 1 ; 0 ) , ось y в точках ( 0 ; − 1 ) и ( 0 ; 1 )

На данной окружности будет три шкалы отсчета – ось x , ось y и сама окружность, на которой мы будем откладывать углы.

Углы на тригонометрической окружности откладываются от точки с координатами ( 1 ; 0 ) , – то есть от положительного направления оси x , против часовой стрелки. Пусть эта точка будет называться S (от слова start). Отметим на окружности точку A . Рассмотрим ∠ S O A , обозначим его за α . Это центральный угол, его градусная мера равна дуге, на которую он опирается, то есть ∠ S O A = α = ∪ S A .

Давайте найдем синус и косинус этого угла. До этого синус и косинус мы искали в прямоугольном треугольнике, сейчас будем делать то же самое. Для этого опустим перпендикуляры из точки A на ось x (точка B ) и на ось игрек (точка C ) .

Отрезок O B является проекцией отрезка O A на ось x , отрезок O C является проекцией отрезка O A на ось y .

Рассмотрим прямоугольный треугольник A O B :

cos α = O B O A = O B 1 = O B

sin α = A B O A = A B 1 = A B

Поскольку O C A B – прямоугольник, A B = C O .

Итак, косинус угла – координата точки A по оси x (ось абсцисс), синус угла – координата точки A по оси y (ось ординат).

Давайте рассмотрим еще один случай, когда угол α – тупой, то есть больше 90 ° :

Опускаем из точки A перпендикуляры к осям x и y . Точка B в этом случае будет иметь отрицательную координату по оси x . Косинус тупого угла отрицательный .

Можно дальше крутить точку A по окружности, расположить ее в III или даже в IV четверти, но мы пока не будем этим заниматься, поскольку в курсе 9 класса рассматриваются углы от 0 ° до 180 ° . Поэтому мы будем использовать только ту часть окружности, которая лежит над осью x . (Если вас интересует тригонометрия на полной окружности, смотрите видео на канале). Отметим на этой окружности углы 0 ° , 30 ° , 45 ° , 60 ° , 90 ° , 120 ° , 135 ° , 150 ° , 180 ° . Из каждой точки на окружности, соответствующей углу, опустим перпендикуляры на ось x и на ось y .

Координата по оси x – косинус угла , координата по оси y – синус угла .

Ещё одно замечание.

Синус тупого угла – положительная величина, а косинус – отрицательная.

Тангенс – это отношение синуса к косинусу. При делении положительной величины на отрицательную результат отрицательный. Тангенс тупого угла отрицательный .

Котангенс – отношение косинуса к синусу. При делении отрицательной величины на положительную результат отрицательный. Котангенс тупого угла отрицательный .

Видео:Тригонометрия. Значения синуса и косинуса углов 0°,90°,180°, 270 °, 360° . 10-11 классСкачать

Основное тригонометрическое тождество

sin 2 α + cos 2 α = 1

Данное тождество – теорема Пифагора в прямоугольном треугольнике O A B :

A B 2 + O B 2 = O A 2

sin 2 α + cos 2 α = R 2

sin 2 α + cos 2 α = 1

Видео:Синус, косинус, тангенс и котангенс углов от 0 до 180 градусов.Скачать

Тригонометрия: Таблица значений тригонометрических функций

0 °30 °45 °60 °90 °sin α01 22 23 21cos α13 22 21 20tg α03 313нетctg αнет313 30

Видео:Как видеть тангенс? Тангенс угла с помощью единичного круга.Скачать

Тригонометрия: градусы и радианы

Как перевести градусы в радианы, а радианы в градусы? Как и когда возникла градусная мера угла? Что такое радианы и радианная мера угла? Ищите ответы в этом видео!

Видео:Уравнение sinx=aСкачать

Тригонометрия: Формулы приведения

Тригонометрия на окружности имеет некоторые закономерности. Если внимательно рассмотреть данный рисунок,

можно заметить, что:

sin 180 ° = sin ( 180 ° − 0 ° ) = sin 0 °

sin 150 ° = sin ( 180 ° − 30 ° ) = sin 30 °

sin 135 ° = sin ( 180 ° − 45 ° ) = sin 45 °

sin 120 ° = sin ( 180 ° − 60 ° ) = sin 60 °

cos 180 ° = cos ( 180 ° − 0 ° ) = − cos 0 °

cos 150 ° = cos ( 180 ° − 30 ° ) = − cos 30 °

cos 135 ° = cos ( 180 ° − 45 ° ) = − cos 45 °

cos 120 ° = cos ( 180 ° − 60 ° ) = − cos 60 °

Рассмотрим тупой угол β :

Для произвольного тупого угла β = 180 ° − α всегда будут справедливы следующие равенства:

sin ( 180 ° − α ) = sin α

cos ( 180 ° − α ) = − cos α

tg ( 180 ° − α ) = − tg α

ctg ( 180 ° − α ) = − ctg α

Видео:Как просто запомнить, что такое sin, cos, tg?! #косинус #синус #тангенс #математика #огэ #егэСкачать

Тригонометрия: Теорема синусов

В произвольном треугольнике стороны пропорциональны синусам противолежащих углов.

a sin ∠ A = b sin ∠ B = c sin ∠ C

Видео:ТРИГОНОМЕТРИЯ С НУЛЯ 😉 #егэ #математика #профильныйегэ #shorts #огэСкачать

Тригонометрия: Расширенная теорема синусов

Отношение стороны к синусу противолежащего угла равно двум радиусам описанной вокруг данного треугольника окружности.

a sin ∠ A = b sin ∠ B = c sin ∠ C = 2 R

Видео:Таблица значений тригонометрических функций - как её запомнить!!!Скачать

Тригонометрия: Теорема косинусов

Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними.

a 2 = b 2 + c 2 − 2 b c ⋅ cos ∠ A

b 2 = a 2 + c 2 − 2 a c ⋅ cos ∠ B

c 2 = a 2 + b 2 − 2 a b ⋅ cos ∠ C

Видео:Формулы приведения - как их легко выучить!Скачать

Примеры решений заданий из ОГЭ

Модуль геометрия: задания, связанные с тригонометрией.

Видео:10 класс, 13 урок, Синус и косинус Тангенс и котангенсСкачать

Тригонометрия: Тригонометрические уравнения

Это тема 10-11 классов.

Из серии видео ниже вы узнаете, как решать простейшие тригонометрические уравнения, что такое обратные тригонометрические функции, зачем они нужны и как их использовать. Если вы поймёте эти базовые темы, то вскоре сможете без проблем решать любые тригонометрические уравнения любого уровня сложности!