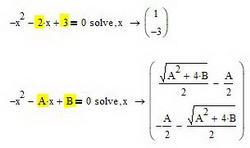Символьное решение уравнений в mathcad

В этом разделе обсуждается, как в символьном виде решать уравнения и системы уравнений. Команда Решить относительно переменной из меню Символика позволяет решить уравнение относительно некоторой переменной и выразить его корни через остальные параметры уравнения.

В этом разделе описывается также, как в символьном виде решить систему уравнений, используя блоки решения уравнений. Для этого требуется Mathcad PLUS.

Решать уравнение символьно гораздо труднее, чем численно. Может оказаться, что в символьном виде решение не существует. Это может быть вызвано рядом причин, обсуждаемых в разделе “Ограничения символьных преобразований”.

Решение уравнения относительно переменной

Чтобы решить уравнение относительно переменной:

• Напечайте уравнение. Убедитесь, что для выведения знака равенства использована комбинация клавиш [Ctrl]=.
• Выделите переменную, относительно которой нужно решить уравнение, щёлкнув на ней мышью.
• Выберите Решить относительно переменной из меню Символика

Mathcad решит уравнение относительно выделенной переменной и вставит результат в рабочий документ. Обратите внимание, что, если переменная возводилась в квадрат в первоначальном уравнении, при решении можно получить два ответа. Mathcad отображает их в виде вектора. Рисунок 20 показывает соответствующий пример.

Рисунок 20: Преобразование выражения для решения уравнения.

Можно также решать неравенство, использующее символы , и . Решения для неравенств будут отображаться в терминах булевых выражений Mathcad. Если имеется более одного решения, Mathcad помещает их в вектор. В Mathcad булево выражение типа x

Исправляем ошибки: Нашли опечатку? Выделите ее мышкой и нажмите Ctrl+Enter

Видео:MathCAD Решение уравнений с помощью функции root 1 вариантСкачать

Символьное решение уравнений в mathcad

Видео:Символьные преобразования в Mathcad (Урок 4)Скачать

Mathcad для студентов

Видео:Использование меню «Символьные операции» в MathCAD 14 (25/34)Скачать

Mathcad для начинающих

Видео:Ключевое слово solve в MathCAD 14 (26/34)Скачать

Скачать программы бесплатно

Видео:Пример решения уравнения в MathCAD 14 (33/34)Скачать

Символьная алгебра в Mathcad

Символьная алгебра в Mathcad включает в себя упрощение и разложение выражений, приведение подобны и разложение на множители.

Операции символьной алгебры можно рассмотреть в сочетании с командами рабочей панели “Символика”, реализующими данную операцию. Перечень некоторых команд и краткое их назначение в Mathcad приведены в таблице.

Видео:Решение систем линейных уравнений в MathCAD 14 (31/34)Скачать

Решение уравнений и систем уравнений в Mathcad

Уравнение и системы уравнений в математическом пакете Mathcad в символьном виде решаются с использованием специального оператора символьного решения solve в сочетании со знаком символьного равенства, который может быть также введен с рабочей панели “Символика”. Например:

Аналогичные действия при решении уравнений в Mathcad можно выполнить, используя меню “Символика”. Для этого необходимо записать вычисляемое выражение. Затем выделить переменную, относительно которой решается уравнение, войти в меню Символика, Переменная, Разрешить. Например:

В случае, если необходимо упростить полученный результат, используется знак равенства [=]. Например:

При решении некоторых уравнений, результат включает большое количество символов. Mathcad сохраняет его в буфере, а на дисплей выводитcя сообщение: “This array has more elements than can be displayed at one time. Try using the “submatrix” function” – “Этот массив содержит больше элементов, чем может быть отображено одновременно. Попытайтесь использовать функцию “submatrix””. В этом случае рекомендуется использовать численное решение. Или, в случае необходимости, символьное решение может быть выведено и отображено на дисплее.

Символьное решение может быть получено с использованием блока given … find. В этом случае при записи уравнения для связи его левой и правой части использует символ логического равенства “=” с панели инструментов Boolean, например:

Аналогичным способом решаются системы уравнений в символьном виде. Ниже приводятся примеры решения систем уравнений в символьном виде различными способами. При использовании оператора символьного решения solve в сочетании со знаком символьного равенства система уравнений должна быть задана в виде вектора, который вводится вместо левого маркера оператора solve, а перечень переменных, относительно которых решается система, вместо правого маркера. Например:

Пример использования блока given…find для решения системы уравнений:

Видео:Символьные вычисления. Операторы solve, simplify, float, expand, coeffs, series. Урок 22Скачать

Символьные вычисления в Mathcad

Результатом математических вычислений в Mathcad могут быть как числовые значения, так и символьные (аналитические) выражения, полученные посредством преобразования исходных математических выражений, описывающих условия задачи и алгоритм ее решения в символьном виде. Основными достоинствами символьных вычислений являются отсутствие погрешности вычислений и универсальность использования в различных прикладных задачах.

Выполнение символьных вычислений

В Mathcad есть несколько основных способов выполнения символьных вычислений.

Символьная алгебра

Разложение на множители, разложение и упрощение выражений.

Решение уравнений и систем уравнений

Для решения уравнений в символьном виде в Mathcad используется специальный оператор символьного решения.

Видео:Mathcad-09. Пример: уравненияСкачать

Выполнение символьных вычислений в Mathcad

Символьные вычисления в математическом пакете Mathcad осуществляется с помощью трёх основных способов:

• при помощи меню “Символика”, обеспечивающего возможность выполнения самых разнообразных символьных вычислений (решение и преобразование символьных выражений, интегрирование, дифференцирование и т.д.);
• при помощи специального оператора символьного ввода, включающего знак символьного равенства [ -> ] , иногда с добавлением операторов панели инструментов “Символика” в Mathcad;
• с использованием стандартных математических функций, в сочетании с символьным знаком равенства.

Видео:Mathcad Prime. Урок 5 - Способы решения уравненийСкачать

Решение уравнений в MathCad

Для решения уравнений в Mathcad можно воспользоваться двумя способами:

Видео:Решение СЛАУ в пакете MathCadСкачать

Использование метода Given — Find:

Это наиболее распространенный способ решения обычных алгебраических уравнений. Он достаточно прост. В рабочем поле записываем слово Given. Это служебное слово. Оно подключает определенные программные модули mathcad для обработки исходных данных, необходимых для решения уравнения численными методами.

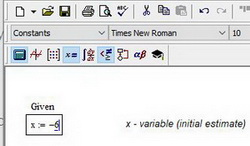
Затем указывается начальное приближение для искомой переменной. Это нужно для увеличения скорости и точности решения уравнения. Если начальное приближение не задать, то mathcad по умолчанию примет его равным нулю

Рис. 1. Ввод данных в поле mathcad

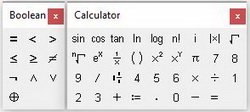
Далее вводится уравнение. Его можно записать в явном или неявном виде. Само уравнение набирается с клавиатуры вручную с использованием панели Calculator. Из этой панели можно взять основные математические операции: дроби, тригонометрию, факториалы и прочее. Уравнение нужно записывать с использованием логического символа «ровно». На панели Boolean он выделен жирным шрифтом (см. рис. 2)

Рис. 2. Панели Boolean и Calculator

После уравнения вводится функция Find(x) (где х — переменная). Это функция, которая возвращает результат. Значение функции Find(x) можно присвоить какой-либо переменной с помощью символа «:=» и использовать ее далее в расчетах

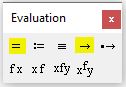
Для получения результата, после Find(x) следует поставить символ «→» либо «=» из панели Evaluation (см. рис. 3). Причем, если вы используете символ «→«, то mathcad определит все корни уравнения и сформирует матрицу результатов. Но если вы используете символ «=«, то mathcad выведет единственный корень, который был наиболее близок к начальному приближению. Так что, если вы не знаете сколько корней имеет уравнение, то лучше использовать стрелочку

Рис. 3. Панель «Evaluation»

В зависимости от сложности уравнения через определенное время MathCad выведет результат. На рис.4 можно рассмотреть синтаксис и различие результатов выводимых mathcad. Обратите внимание, что выводимые результаты одного и того же уравнения различны

Рис. 4. Результат численного решения уравнения

Mathcad позволяет решать уравния в символьном виде. Например, если мы заменим все числовые константы на неизвестные параметры и решим уравнение относительно x, то результат выведется в символьном виде (см. рис. 5). Причем, обратите внимание, что в данном случае нам не нужно вводить начальное приближение и мы должны использовать символ «→» для вывода результата

Рис. 5. Результат символьного решения уравнения

Видео:MathCAD. Given - FindСкачать

Использование метода Solve:

Этот метод отличается от выше рассмотренного синтаксисом. На свободном поле вводим уравнение с использованием логического символа «ровно» из панели Boolean. После ввода уравнения, не смещая курсор ввода, на панели Symbolic нажимаем кнопку solve (см. рис. 6)

Рис. 6. Панель Symbolic

Затем ставим запятую и вводим переменную, относительно которой нужно решить уравнение (в нашем случае это x). Нажимаем Enter на клавиатуре и смотрим результат (см. рис. 7)

Рис. 7. Результат решения уравнения методом Solve

Обратите внимание, что метод подходит как для численного так и для символьного представления результатов

Как показывает моя личная инженерная практика, иногда не удается решить уравнения с помощью Given — Find, но получается в Solve. При этом, к сожалению, метод Solve не очень удобен для далнейшего использования результатов решения уравнения

Donec eget ex magna. Interdum et malesuada fames ac ante ipsum primis in faucibus. Pellentesque venenatis dolor imperdiet dolor mattis sagittis. Praesent rutrum sem diam, vitae egestas enim auctor sit amet. Pellentesque leo mauris, consectetur id ipsum sit amet, fergiat. Pellentesque in mi eu massa lacinia malesuada et a elit. Donec urna ex, lacinia in purus ac, pretium pulvinar mauris. Curabitur sapien risus, commodo eget turpis at, elementum convallis elit. Pellentesque enim turpis, hendrerit tristique.

Lorem ipsum dolor sit amet, consectetur adipiscing elit. Duis dapibus rutrum facilisis. Class aptent taciti sociosqu ad litora torquent per conubia nostra, per inceptos himenaeos. Etiam tristique libero eu nibh porttitor fermentum. Nullam venenatis erat id vehicula viverra. Nunc ultrices eros ut ultricies condimentum. Mauris risus lacus, blandit sit amet venenatis non, bibendum vitae dolor. Nunc lorem mauris, fringilla in aliquam at, euismod in lectus. Pellentesque habitant morbi tristique senectus et netus et malesuada fames ac turpis egestas. In non lorem sit amet elit placerat maximus. Pellentesque aliquam maximus risus, vel venenatis mauris vehicula hendrerit.

Interdum et malesuada fames ac ante ipsum primis in faucibus. Pellentesque venenatis dolor imperdiet dolor mattis sagittis. Praesent rutrum sem diam, vitae egestas enim auctor sit amet. Pellentesque leo mauris, consectetur id ipsum sit amet, fersapien risus, commodo eget turpis at, elementum convallis elit. Pellentesque enim turpis, hendrerit tristique lorem ipsum dolor.

🌟 Видео

Средство для решения систем уравнений в MathCAD 14 (29/34)Скачать

Работа с MathCad Prime. Решение дифференциальных уравнений.Скачать

MathCAD Решение системы уравненийСкачать

1 Одно уравнениеСкачать

Mathcad Prime. Урок 3 - Символьные преобразованияСкачать

Лекция 13 Символьные вычисленияСкачать