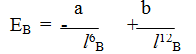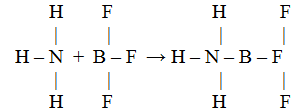Силы межмолекулярного взаимодействия в газах уравнение ван дер ваальса

степени расстояния между ними или второй степени объема, занимаемого газом. Считается также, что силы притяжения суммируются с внешним давлением. С учетом этих соображений уравнение состояния идеального газа преобразуется в уравнение Ван-дер-Ваальса

Реальные газы — газы, свойства которых зависят от взаимодействия молекул. В обычных условиях, когда средняя потенциальная энергия межмолекулярного взаимодействия много меньше средней кинетической энергии молекул, свойства реальных и идеальных газов отличаются незначительно. Поведение этих газов резко различно при высоких давлениях и низких температурах, когда начинают проявляться квантовые эффекты.

3.7.2. Силы межмолекулярного взаимодействия

Ван-дер-Ваальс, объясняя свойства реальных газов и жидкостей, предположил, что на малых расстояниях между молекулами действуют силы отталкивания, которые с увеличением расстояния сменяются силами притяжения. Межмолекулярные взаимодействия имеют электрическую природу и складываются из сил притяжения (ориентационных, индукционных) и сил отталкивания.

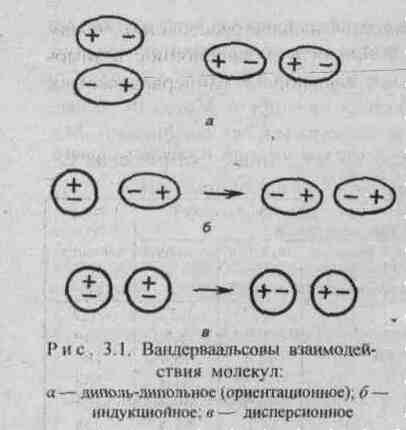
Ориентационные силы действуют между полярными молекулами — молекулами, обладающими дипольными или квадрупольными моментами. Сила притяжения между молекулами зависит от их взаимной ориентации, поэтому они и называются ориентационными. Хаотическое тепловое движение непрерывно меняет ориентацию полярных молекул, но среднее по всем ориентациям значение силы не равно нулю (рис. 3.7.1).

Среднее значение потенциальной энергии ориентационного межмолекулярного взаимодействия равно . где p1, Р2 — дипольные моменты взаимодействующих молекул. Сила ориентационного взаимодействия . убывает с расстоянием значительно быстрее, чем кулоновская сила взаимодействия заряженных частиц.

Видео:Уравнение Ван-дер-Ваальса | Газы.Молекулярно-кинетическая теория | Химия (видео 8)Скачать

Взаимодействия между молекулами. Вандерваальсовы силы

» data-shape=»round» data-use-links data-color-scheme=»normal» data-direction=»horizontal» data-services=»messenger,vkontakte,facebook,odnoklassniki,telegram,twitter,viber,whatsapp,moimir,lj,blogger»>

Взаимодействия между молекулами.

При сближении молекул появляется притяжение, что обусловли­вает возникновение конденсированного состояния вещества. К основ­ным видам взаимодействия молекул следует отнести вандерваальсовы силы, водородные связи и донорно-акцепторное взаимодействие.

4.8.1. Вандерваальсовы силы. В 1873 г. голландский ученый И. Ван-дер-Ваальс предположил, что существуют силы, обусловливающие притяжение между молеку­лами. Эти силы позднее получили название вандерваальсовых сил. Они включают в себя три составляющие: диполь-дипольное, индукционое и дисперсионное взаимодействия.

Диполь-дипольное взаимо­действие. При сближении по­лярных молекул они ориенти­руются таким образом, чтобы положительная сторона одного диполя была ориентирована к отрицательной стороне другого диполя (рис.3.1). Возникающее между диполя­ми взаимодействие называется диполь-дипольным или ориентационным. Энергия диполь-дипольного взаимодействия пропорциональна электрическому моменту диполя в четвертой сте­пени и обратно пропорциональна расстоянию между центрами диполей в шестой степени и абсолют­ной температуре в первой степени.

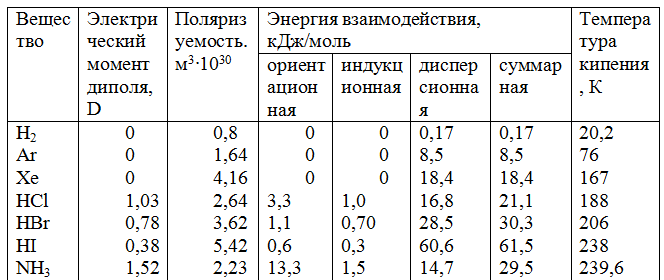
Индукционное взаимодействие. Диполи могут воздействовать на неполярные молекулы, превращая их в индуцированные (наве­денные) диполи (рис.3.1). Между постоянными и наведенными ди­полями возникает притяжение, энергия которого пропорциональна электрическому моменту диполя во второй степени и обратно про­порциональна расстоянию между центрами молекул в шестой степе­ни. Энергия индукционного взаимодействия возрастает с увеличени­ем поляризуемости молекул, т.е. способности молекулы к об­разованию диполя под воздействием электрического поля. Величину поляризуемости выражают в единицах объема. Поляризуемость в од­нотипных молекулах растет с увеличением размера молекул (табл. 14). Энергия индукционного взаимодействия значительно меньше энер­гии диполь-дипольного взаимодействия (табл. 14).

Дисперсионное притяжение. В любой молекуле или атоме бла­городного газа возникают флуктуации электрической плотности, в результате чего появляются мгновенные диполи, которые в свою очередь индуцируют мгновенные диполи у соседних молекул (рис.3.1). Движение мгновенных диполей становится согласованным, их появление и распад происходит синхронно. В результате взаимо­действия мгновенных диполей энергия системы понижается. Энергия дисперсионного взаимодействия пропорциональна поляризуемости молекул и обратно пропорциональна расстоянию между центрами частиц. Для неполярных молекул дисперсионное взаимо­действие является единственной составляющей вандерваальсовых сил (табл. 14).

Таблица 14. Вклад отдельных составляющих в энергию межмолекулярного взаимодействия

Энергия вандерваальсова взаимодействия. Энергия всех видов вандерваальсова взаимодействия обратно пропорциональна расстоя­нию между центрами молекул в шестой степени.

При сильном сближении молекул проявляются силы отталкивания между ними, которые обратно пропорциональны расстоянию: между молекулами-в двенадцатой ступени. Поэтому зависимость результирующей энергии вандерваальсова взаимодействия Е_в от расстояния между молекулами, I_в, выражается уравнением

где: а и b — постоянные.

Минимальная энергия системы обеспечивается при расстояниях между центрами молекул 0,4÷0,5 нм, т.е. существенно больше длины химической связи/

Как видно из табл. 14, с увеличением размера молекул в ряду Аr—Хе и НС1—HI растет их поляризуемость и энергия дисперсион­ного притяжения. Ориентационное взаимодействие вносит значи­тельный вклад в вандерваальсовы силы лишь в случае молекул с большим электрическим моментом диполя. С увеличением сум­марной энергии межмолекулярного взаимодействия возрастает температура кипения жидкостей, а также теплота их испарения.

Суммарная энергия вандерваальсового взаимодействия молекул на 1—2 порядка ниже энергии химических связей.

Итак, между молекулами возникают относительно слабые вандерваальсовы взаимодействия, включающие дисперсионные силы, а для полярных молекул и диполь-дипольное притяжение и индукци­онные взаимодействия.

4.8.2. Донорно-акцепторное взаимодействие молекул. Комплексные соединения. Если одна из двух молекул имеет атом со свободными орбиталями, а другая – атом с парой неподеленных электронов, то между ними происходит донорно-акцепторное взаимодействие, которое приводит к образованию ковалентной связи, например:

У атома азота в молекуле аммиака имеется неподеленная пара электронов, а у атома бора в молекуле трифторида бора – вакантная орбиталь.

При взаимодействии по донорно-акцепторному механизму атом азота отдает на связь пару электронов, а атом бора – вакантную орби­таль, в результате чего возникает ковалентная связь

В полученном соединении суммарные валентности бора и азота равны четырем.

Комплексы. Аналогичным образом образуется соединение КРF₆ при взаимодействии KF и PF₅, которое можно записать в виде К[РF₆].

При взаимодействии сульфата меди и аммиака образуется сложное соединение

которое выражается формулой [Сu(NН₃)₄]SO₄. Сложные соединения, у которых имеются ковалентные связи, образованные по донорно-акцепторному механизму, получили название комплексных или коор­динационных соединений.

Видео:Силы Ван-дер-Ваальса (видео 1) | Силы межмолекулярного взаимодействия | ХимияСкачать

Силы межмолекулярного взаимодействия в газах уравнение ван дер ваальса

Предпринималось много попыток для учета отклонений свойств реальных газов от свойств идеального газа путем введения различных поправок в уравнение состояния идеального газа. Наибольшее распространение вследствие простоты и физической наглядности получило уравнение Ван-дер-Ваальса (1873).

Первая поправка в уравнении состояния идеального газа рассматривает собственный объем, занимаемый молекулами реального газа. В уравнении Дюпре (1864)

постоянная b учитывает собственный мольный объем молекул.

При понижении температуры межмолекулярное взаимодействие в реальных газах приводит к конденсации (образование жидкости). Межмолекулярное притяжение эквивалентно существованию в газе некоторого внутреннего давления (иногда его называют статическим давлением). Изначально величина была учтена в общей форме в уравнении Гирна (1865)

(p + ) (V – nb) = nRT. (1.4)

Ван-дер-Ваальс в 1873 г. дал функциональную интерпретацию внутреннего давления. Согласно модели Ван-дер-Ваальса, силы притяжения между молекулами (силы Ван-дер-Ваальса) обратно пропорциональны шестой степени расстояния между ними, или второй степени объема, занимаемого газом. Считается также, что силы притяжения суммируются с внешним давлением. С учетом этих соображений уравнение состояния идеального газа преобразуется в уравнение Ван-дер-Ваальса:

(1.5)

или для одного моля

. (1.6)

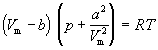
Значения постоянных Ван-дер-Ваальса a и b, которые зависят от природы газа, но не зависят от температуры, приведены в таблице 1.3.

Таблица 1.3. Постоянные Ван-дер-Ваальса для различных газов

Уравнение (1.6) можно переписать так, чтобы выразить в явном виде давление

(1.7)

(1.8)

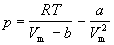
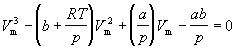
Уравнение (1.8) содержит объем в третьей степени и, следовательно, имеет или три действительных корня, или один действительный и два мнимых. При высоких температурах уравнение (1.8) имеет один действительный корень, и по мере повышения температуры кривые, вычисленные по уравнению Ван-дер-Ваальса, приближаются к гиперболам, соответствующим уравнению состояния идеального газа.

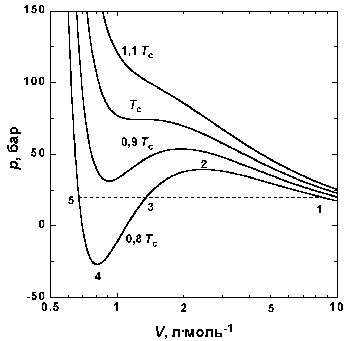Рис.1.4 Изотермы Ван-дер-Ваальса для СО2

На рис. 1.4 (стр. 7) приведены изотермы, вычисленные по уравнению Ван-дер-Ваальса для диоксида углерода (значения констант a и b взяты из табл. 1.3). Из рисунка видно, что при температурах ниже критической (31,04 °С) вместо горизонтальных прямых, соответствующих равновесию жидкости и пара, получаются волнообразные кривые 12345 с тремя действительными корнями, из которых только два, 1 и 5, физически осуществимы. Третий корень (точка 3) физически не реален, поскольку находится на участке кривой 234, противоречащем условию стабильности термодинамической системы 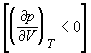. Состояния на участках 12 и 54, которые соответствуют переохлажденному пару и перегретой жидкости, соответственно, являются неустойчивыми (метастабильными) и могут быть лишь частично реализуемы в специальных условиях. Так, осторожно сжимая пар выше точки 1 (рис. 1.4), можно подняться по кривой 12. Для этого необходимо отсутствие в паре центров конденсации, и в первую очередь пыли. В этом случае пар оказывается в пересыщенном, т.е. переохлажденном состоянии. И наоборот, образованию капелек жидкости в таком паре способствуют, например, попадающие в него ионы. Это свойство пересыщенного пара используется в известной камере Вильсона (1912), применяемой для регистрации заряженных частиц. Движущаяся заряженная частица, попадая в камеру, содержащую пересыщенный пар, и соударяясь с молекулами, образует на своем пути ионы, создающие туманный след – трек, который фиксируется фотографически.

Согласно правилу Максвелла (the Maxwell construction), которое имеет теоретическое обоснование, для того, чтобы расчетная кривая соответствовала экспериментальной равновесной изотерме, нужно вместо кривой 12345 провести горизонтальную прямую 15 так, чтобы площади 1231 и 3453 были равны. Тогда ордината прямой 15 будет равна давлению насыщенного пара, а абсциссы точек 1 и 5 – мольным объемам пара и жидкости при данной температуре.

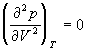
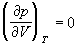
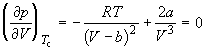
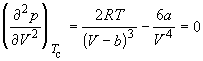
По мере повышения температуры все три корня сближаются, и при критической температуре T_c все три корня становятся равными. В критической точке изотерма Ван-дер-Ваальса имеет точку перегиба [] с горизонтальной касательной [], то есть

, (1.9)

. (1.10)

Совместное решение этих уравнений дает:

, (1.11)

, (1.12)

, (1.13)

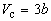
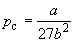
что позволяет определять константы уравнения Ван-дер-Ваальса из критических параметров газа. Соответственно, согласно уравнению Ван-дер-Ваальса, критический фактор сжимаемости Z_c для всех газов должен быть равен

(1.14)

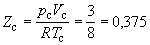
Из таблицы 1.2 видно, что хотя значение Z_c для реальных газов приблизительно постоянно (0,27 – 0,30 для неполярных молекул), оно все же заметно меньше вытекающего из уравнения Ван-дер-Ваальса. Для полярных молекул наблюдается еще большее расхождение.

Принципиальное значение уравнения Ван-дер-Ваальса определяется следующими обстоятельствами:

1) уравнение было получено из модельных представлений о свойствах реальных газов и жидкостей, а не явилось результатом эмпирического подбора функции f(p,V,T), описывающей свойства реальных газов;

2) уравнение долго рассматривалось как некоторый общий вид уравнения состояния реальных газов, на основе которого было построено много других уравнений состояния (см. ниже);

3) с помощью уравнения Ван-дер-Ваальса впервые удалось описать явление перехода газа в жидкость и проанализировать критические явления. В этом отношении уравнение Ван-дер-Ваальса имеет преимущество даже перед более точными уравнениями в вириальной форме (см. 1.1, 1.2).

Причиной недостаточной точности уравнения Ван-дер-Ваальс считал ассоциацию молекул в газовой фазе, которую не удается описать, учитывая зависимость параметров a и b от объема и температуры, без использования дополнительных постоянных. После 1873 г. сам Ван-дер-Ваальс предложил еще шесть вариантов своего уравнения, последнее из которых относится к 1911 г. и содержит пять эмпирических постоянных. Две модификации уравнения (1.5) предложил Клаузиус, и обе они связаны с усложнением вида постоянной b. Больцман получил три уравнения этого типа, изменяя выражения для постоянной a. Всего известно более сотни подобных уравнений, отличающихся числом эмпирических постоянных, степенью точности и областью применимости. Выяснилось, что ни одно из уравнений состояния, содержащих менее 5 индивидуальных постоянных, не оказалось достаточно точным для описания реальных газов в широком диапазоне p, V, T, и все эти уравнения оказались непригодными в области конденсации газов. Из простых уравнений с двумя индивидуальными параметрами неплохие результаты дают уравнения Дитеричи и Бертло (см. табл. 1.4).

Сервер создается при поддержке Российского фонда фундаментальных исследований
Не разрешается копирование материалов и размещение на других Web-сайтах
Вебдизайн: Copyright (C) И. Миняйлова и В. Миняйлов
Copyright (C) Химический факультет МГУ
Написать письмо редактору

🔥 Видео

Урок 194. Уравнение Ван-дер-ВаальсаСкачать

Уравнение Ван дер ВаальсаСкачать

Основы теплотехники. Реальные газы. Уравнение Ван дер Ваальса. Решение задач.Скачать

1 3 Водородная связь Ван дер Ваальсовы силыСкачать

Реальный газ Уравнение Ван-Дер-ВаальсаСкачать

Уравнение Ван дер Ваальса. Часть 1. Межмолекулярные взаимодействия. Изотермы Ван дер Ваальса.Скачать

Как жуки используют силы Ван-дер-Ваальса?Скачать

Караваев В. А. - Молекулярная физика - Газ Ван-дер-Ваальса. Силы межмолекулярного взаимодействияСкачать

Уравнение Ван-дер-Ваальса и опыт Джоуля и ТомсонаСкачать

Силы взаимодействия молекул. 10 класс.Скачать

270. Силы Ван-дер-ВаальсаСкачать

Бушина Т. А. - Молекулярная физика - Реальные газы. Уравнение Ван-дер-ВаальсаСкачать

Реальные газы. Изотермы Эндрюса и Ван-Дер-Ваальса. Метастабильные состоянияСкачать

Поверхностное натяжение (видео 3) | Силы межмолекулярного взаимодействия | ХимияСкачать

Водородная связь. 10 класс.Скачать

Уравнение Ван-дер-Ваальса (вывод и применение). By Bogatov N.A.Скачать

Урок 83. Межмолекулярные взаимодействия.Скачать

Андреенко А. С. - Общая физика для геологов - Уравнение Ван-дер-ВаальсаСкачать