Исследование объективно существующих связей между явлениями — важнейшая задача статистики. В процессе статистического исследования зависимостей выявляются причинно-следственные отношения между явлениями. Причинно-следственные отношения — это такая связь явлений и процессов, когда изменение одного из них — причины ведет к изменению другого — следствия.
Признаки явлений и процессов по их значению для изучения взаимосвязи делятся на два класса. Признаки, обуславливающие изменения других, связанных с ними признаков, называют факторными, или просто факторами. Признаки, изменяющиеся под действием факторных признаков, называют результативными.
В статистике различают функциональные и стохастические (вероятностные) связи явлений и процессов:
- Функциональной называют такую связь, при которой определенному значению факторного признака соответствует одно значение результативного.
- Если причинная зависимость проявляется не в каждом отдельном случае, а в общем, среднем при большом числе наблюдений, то такая зависимость называется стохастической (вероятностной). Частным случаем стохастической связи является корреляционная связь.
Кроме того, связи между явлениями и их признаками классифицируются по степени тесноты, направлению и аналитическому выражению.
По направлению выделяют связь прямую и обратную:
- Прямая связь — это такая связь, при которой с увеличением (уменьшением) значений факторного признака происходит увеличение (уменьшение) значений результативного. Так, например, рост производительности труда способствует увеличению уровня рентабельности производства.
- В случае обратной связи значения результативного признака изменяются под воздействием факторного, но в противоположном направлении по сравнению с изменением факторного признака. Так с увеличением уровня фондоотдачи снижается себестоимость единицы производимой продукции.
По аналитическому выражению выделяют связи прямолинейные (или просто линейные) и нелинейные:
- Если статистическая связь между явлениями может быть приблизительно выражена уравнением прямой линии, то ее называют линейной связью вида: у=а+bх.
- Если же связь может быть выражена уравнением какой-либо кривой линии (параболы, гиперболы и др.), то такую связь называют нелинейной (криволинейной) связью.
Теснота связи показывает меру влияния факторного признака на общую вариацию результативного признака. Классификация связи по степени тесноты представлена в таблице 1.
| Величина коэффициента корреляции | Характер связи |
|---|---|
| До ±3 | Практически отсутствует |
| От ±3 до ±0,5 | Слабая |
| От ±0,5 до ±0,7 | Умеренная |
| От ±0,7 до ±1,0 | Сильная |
Для выявления наличия связи, ее характера и направления в статистике используются следующие методы: приведения параллельных данных, аналитических группировок, графический, корреляции. Основным методом изучения статистической взаимосвязи является статистическое моделирование связи на основе корреляционного и регрессионного анализа.
Корреляция — это статистическая зависимость между случайными величинами, не имеющая строго функционального характера, при которой изменение одной из случайных величин приводит к изменению математического ожидания другой. В статистике принято различать следующие виды корреляции:
- парная корреляция — связь между двумя признаками (результативным и факторным, или двумя факторными);
- частная корреляция — зависимость между результативным и одним факторным признаками при фиксированном значении других факторных признаков;
- множественная корреляция — зависимость результативного и двух или более факторных признаков, включенных в исследование.
Задачей корреляционного анализа является количественное определение тесноты связи между двумя признаками (при парной связи) и между результативным и множеством факторных признаков (при многофакторной связи).
Теснота связи количественно выражается величиной коэффициентов корреляции, которые давая количественную характеристику тесноты связи между признаками, позволяют определять «полезность» факторных признаков при построении уравнения множественной регрессии.
Корреляция взаимосвязана с регрессией, поскольку первая оценивает силу (тесноту) статистической связи, вторая исследует ее форму.
Регрессионный анализ заключается в определении аналитического выражения связи в виде уравнения регрессии.
Регрессией называется зависимость среднего значения случайной величины результативного признака от величины факторного, а уравнением регрессии – уравнение описывающее корреляционную зависимость между результативным признаком и одним или несколькими факторными.
Формулы корреляционно-регрессионного анализа для прямолинейной связи при парной корреляции представлены в таблице 2.
| Показатель | Обозначение и формула | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Уравнение прямой при парной корреляции | yx = a +bx, где b — коэффициент регрессии | ||||||||||
| Система нормальных уравнений способом наименьших квадратов для определения коэффициентов a и b |  | ||||||||||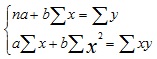
| Линейный коэффициент корреляции для определения тесноты связи, его интерпретация: r = 0 – связь отсутствует; 0 2012 © Лана Забродская. При копировании материалов сайта ссылка на источник обязательна Видео:ЛИНЕЙНЫЕ УРАВНЕНИЯ - Как решать линейные уравнения // Подготовка к ЕГЭ по МатематикеСкачать  Понятие и показатели силы связи в линейной регрессииСила связи характеризует, на сколько единиц в среднем изменится результат при изменении фактора на одну единицу. ∆ 1) абсол. показатель – коэф-т регрессии (изменение результата при изм-ии фактора на 1 ед.). Он хар-ет также направление связи (если b>0, то связь прямая, если b Показатели тесноты связи показывают насколько фактор или факторы, включенные в модель регрессии, объясняют изменение результата. Величина Поэтому для того, чтобы получить показатель тесноты связи, придумали использовать правило сложения дисперсий. Это правило изучалось на лекциях по статистике для аналитической группировки, для линейной дисперсии это правило выглядит следующим образом:
Можно сделать вывод о том, что деление на n можно опустить, тогда ничего не изменится:
Где
Если Можно, в принципе, использовать данное выражение как показатель тесноты связи, но удобнее, чтобы тесная связь была, когда ближе к 1. Поэтому рассмотрим другую формулу (которая и представляет собой показатель тесноты связи):
Если SSocm большая, то показатель стремится к нулю, и связь слабая. Для линейных функций этот показатель называется коэффициентом детерминации, а если факторов много, то называется коэффициентом множественной детерминации.
Из правил сложения дисперсий следует:
С ним есть функционально связанный показатель — коэффициент корреляции (или коэффициент множественной корреляции, если факторов много):
Для того, чтобы оценить, насколько тесна связь, используется шкала Чеддока (о силе связи судит, только по абсолютному значению 0,1 – 0,3 — связь слабая 0,3 – 0,5 — связь умеренная 0,5 – 0,7 — связь заметная 0,7 – 0,9 — связь тесная 0,9 – 0,99 — связь очень тесная — доля факторной дисперсии в общей дисперсии результата. Следовательно, вариация валового дохода на 76% обусловлена вариацией факторов, включенных в модель регрессии, то есть вариацией среднегодовой стоимости основных фондов и оборотных средств.
Эта формула действует хороша только для парной регрессии.
Следовательно: Видео:Линейное уравнение с двумя переменными. 7 класс.Скачать  Понятие и показатели силы связи в линейной регрессии
Сила связи определяет величину изменения зависимой переменной при единичном изменении независимой. Сила связи показывает, как изменится результат при изменении фактора. В уравнении парной линейной регрессии: коэффициент b измеряет силу связи и является абсолютным показателем силы связи. Коэффициент регрессии b показывает среднее изменение результата с изменением фактора на одну единицу (с увеличением x на одну единицу b возрастает в среднем на …). Знак при b показывает направление связи: b > 0 – связь прямая; b связь тесная => 1. Коэффициент детерминации
Показывает, на сколько результат обусловлен факторами, включенными в уравнение регрессии. 2. Коэффициент множественной корреляции
Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.006 сек.) 📹 ВидеоЛинейное уравнение. Что это?Скачать  Математика это не ИсламСкачать  Линейное уравнение с одной переменной. 6 класс.Скачать  Как решать линейные уравнения #математика #математика7классСкачать  Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать  ЛИНЕЙНОЕ УРАНЕНИЕ С ДВУМЯ ПЕРЕМЕННЫМИ — Как решать линейное уравнение // Алгебра 7 классСкачать  Как решать линейные уравнения?Скачать  Линейное уравнение.Скачать  Как решать уравнения? уравнение 7 класс. Линейное уравнениеСкачать  Урок 7 ЛИНЕЙНОЕ УРАВНЕНИЕ С ОДНОЙ ПЕРЕМЕННОЙСкачать  Алгебра 7 Линейное уравнение с одной переменнойСкачать  Линейное уравнение с двумя переменными.Скачать  Линейные уравнения с одной переменной, содержащие переменную под знаком модуля. 6 класс.Скачать  Решение уравнений, сводящихся к линейным | Алгебра 7 класс #18 | ИнфоурокСкачать  Линейное уравнение с одной переменнойСкачать  ОГЭ Как из уравнения с дробью получить обычное линейное уравнение #огэ#огэ2023#алгебра#огэматематикаСкачать  Линейные уравнения ЕГЭ Математика базовый уровень (ТИП 17)Скачать  Связь импульса силы и импульса телаСкачать  |
— прямая связь. Сила связи больше, где больше ∆y.
y Различают след. показатели силы связи:
характеризует тесноту связи (чем он меньше, тем связь теснее), с помощью метода наименьших квадратов мы оптимизировали эти отклонения. 
характеризует разброс точек, тесноту связи.Эта величина является характеристикой связи, но ее нельзя использовать как показатель связи ввиду следующего недостатка: данная величина зависит от единиц измерения исходных показателей, если исходные показатели имеют разные единицы измерения, то тогда показатели будут несопоставимы.
общая сумма квадратов 
. — факторная сумма квадратов: 
— остаточная сумма квадратов. Основной недостаток суммы квадратов в его размерности, но оказывается, что это часть от общей суммы:
, тогда связь максимально тесная. Ограничение такое, так как у нас часть целого:
Чем ближе к нулю, тем связь теснее, чем ближе к единице, тем связь слабее по этой формуле.
, т.е берем по модулю, а, вообще, он может быть и отриц. и положит.):
Выводы по R: допустим, 
=0,76 
, а значит, что связь между валовым доходом и среднегодовой стоимостью основных фондов и оборотных средств тесная. Выводы по 
делаются глядя на
— обычно для множ регрессии, а если парная линейная регрессия, то
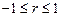. Если r=0,72, то связь тесная (смотрим на модуль) минус показывает, что связь обратная.
стремится к 1.
