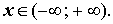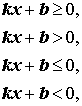Видео:Как решать неравенства? Математика 10 класс | TutorOnlineСкачать
Шпаргалки по математике, алгебре и геометрии Шпаргалки по физике / Шпаргалки по химии
| Таблица квадратов. Таблица степеней. Формулы сокращенного умножения. Модуль числа. Свойства модуля: | Уравнения и неравенства с модулем. Последовательности и прогрессии. Метод кординат на плоскости. Скалярное произведение векторов. Расстояние между точками. | Тригонометрия — основные формулы. Таблица значений тригонометрических функций. Решение тригонометрических уравнений: | Четность и нечетность тригонометрических функций. Обратные тригонометрические функции. Формулы приведения. Знаки тригонометрических функций. Показательные уравнения и неравенства. |
 |  |  |  |
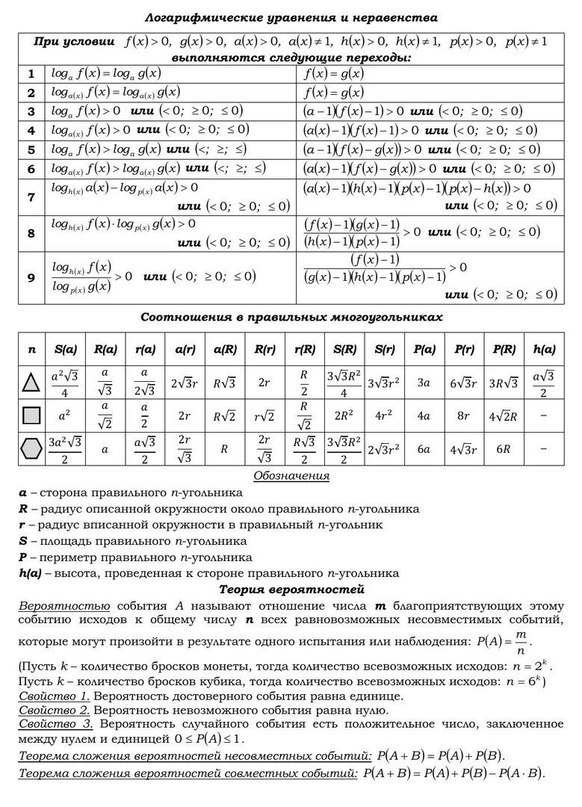
| Корень n-ой степени. Степени. Иррациональные уравнения и неравенства. Логарифм, свойства логарифмов | Логарифмические уравнения и неравенства. Соотношения в правильных многоугольниках. Теория вероятностей. Теоремы сложения вероятностей. | Логарифмические уравнения и неравенства. | Производная. Правила дифференцирования. Производная сложной функции. Уравнение касательной к графику функции в точке. |
 |  |  |  |
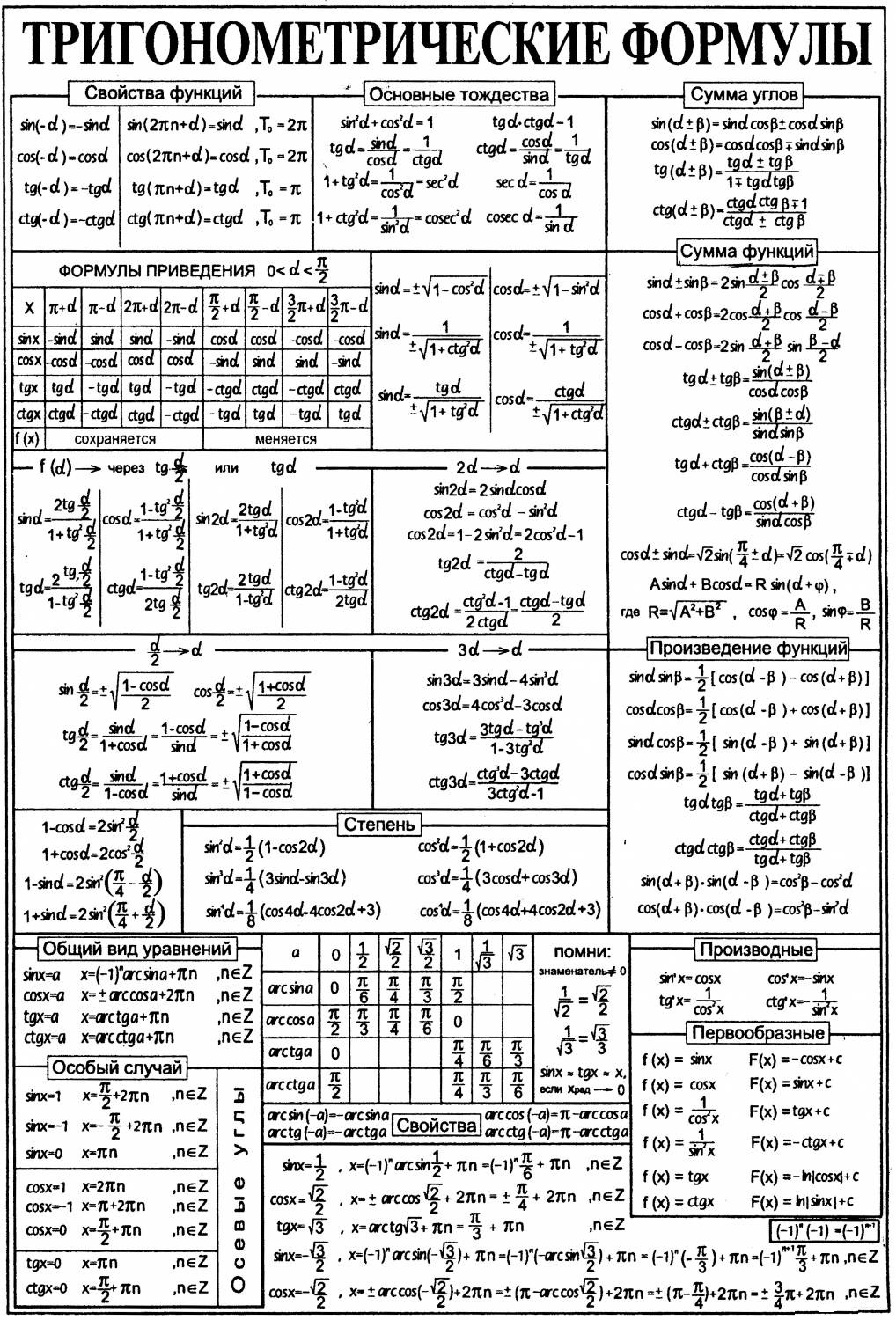
| Тригонометрические формулы. Свойства функций, основные тождества, сумма углов. Сумма функций, формулы приведения, особые случаи, степени, половинные, двойные и тройные углы. Обратные функции. | |||
 |
| Набор 2 — Алгебра. Линейная алгебра. | |||
| Свойства степеней. Формулы сокращенного умножения. Свойства арифметических корней. Модуль. Начала математического анализа: прогрессии арифметическая и геометрическая. Производная. Первообразная и интеграл. Среднее арифметическое и среднее геометрическое. | Тригонометрия. Основные формулы. Арксинус, арккосинус, арктангенс, арккотангенс. Четность функций. Значения тригонометрических функций некоторых углов. | Графики некоторых элементарных функций. Логарифмы. Решение квадратных, иррациональных, показательных, тригонометрических уравнений, уравнений с модулем | Квадратные неравенства. Неравенства с модулем. Логарифмические неравенства. Неравенства с модулем. Иррациональные неравенства. Показательные неравенства. Комбинаторика и бином Ньютона. |
 |  |  |  |
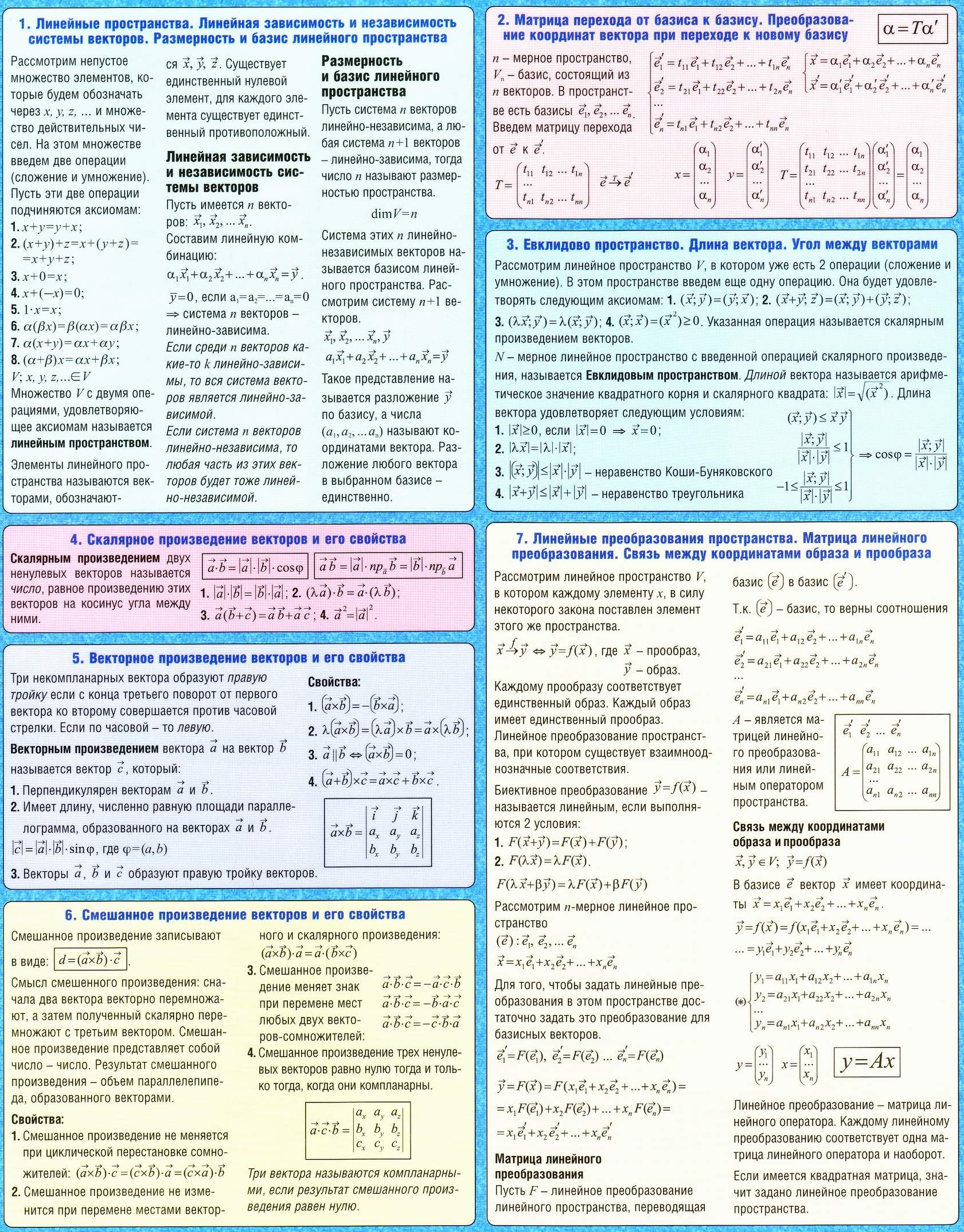
| Определение комплексного числа. Геометрическая интерпретация комплексного числа. Тригонометрическая форма комплексного числа. Показательная форма комплексного числа. Действия с комплексными числами. Последовательности, пределы последовательности. Теоремы о пределах числовых последовательностей. | Определение предела числовой функции. Односторонние пределы. Свойства пределов. Непрерывные функции и их свойства. Точки разрыва и их классификации. Замечательные пределы. Важные пределы. Теоремы о среднем. Правило Лопиталя. | Линейные пространства. Линейная зависимость и независимость системы векторов. Размерность и базис линейного пространства. Скалярное и векторное произведение векторов. Смешанное произведение векторов. Матрица перехода от базиса к базису. Преобразование координат вектора при переходе к новому базису. Евклидово пространство. Длина вектора. Угол между векторами. Линейные преобразования пространства. Матрица линейного преобразования. Связь между координатами образа и прообраза. | Связь между координатами одного и того же линейного оператора в разных базисах. Угол между прямой и плоскостью. Расстояние от точки до плоскости. Характеристические уравнения линейного оператора. Собственные векторы линейного оператора и их свтойства. Поверхности второго порядка. Плоскость в пространстве. Виды углов в пространстве. Уравнения плоскости. |
 |  |  |  |
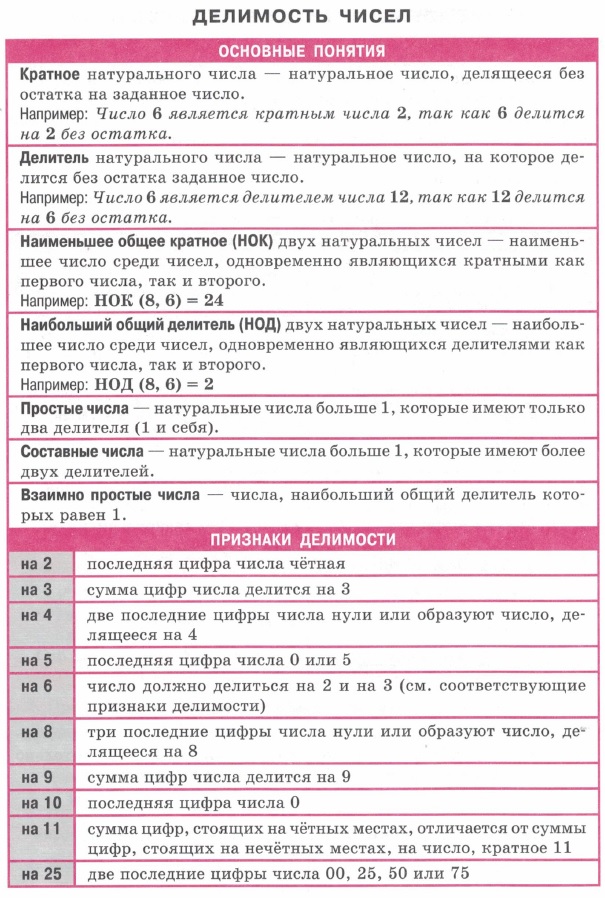
| Делимость чисел. Кратное. Делитель. НОК. НОД Простые и составные числа. Взаимно простые числа. | Числовые последовательности, члены, способы задания. Арифметическая и геометрическая прогрессии. Формулы. Характеристические свойства | Числа. Множества натуральных, целых, рациональных, действительных, иррациональных чисел. Арифметические действия с дробями. Модуль — свойства. | Решение квадратных уравнений. Формулы дискриминанта. Решение неполных квадратных уравнений. Теорема Виета. Алгоритм решения квадратного неравенства. |
 |  |  |  |
| Основные свойства функций. Понятие функции. Четность и нечетность. Периодичность. Нули функции. Промежутки знакопостоянства. Монотонность (возрастание, убывание). Асимптоты. Алгоритм описания фукнкции. | Преобразование графиков функций у= f(x) в y=-f(x); y=f(-x); y=-f(-x); y=f(x-a); y=f(x)+b; y=f(ax); y=kf(x); y=|f(x)|; y=f(|x|). Построение графика обратной функции | ||
 |  | ||
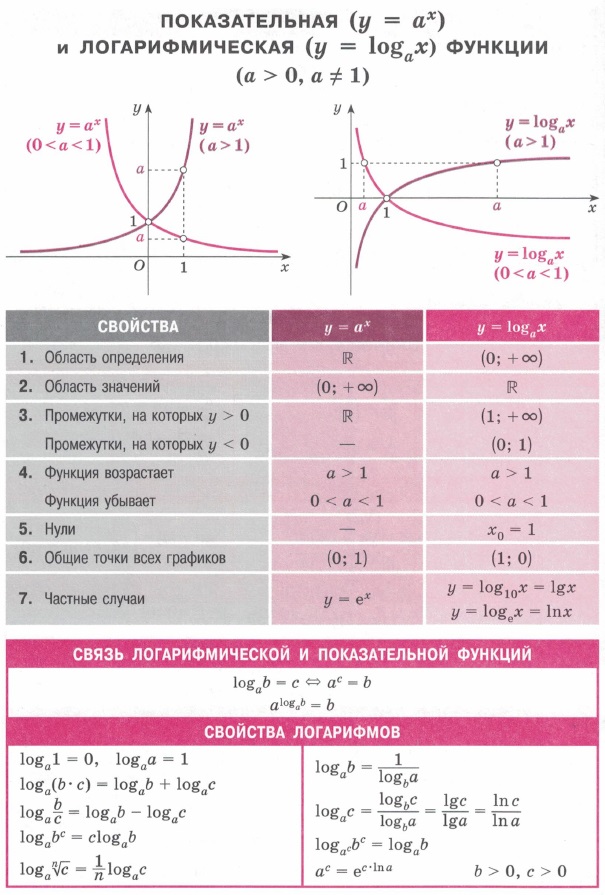
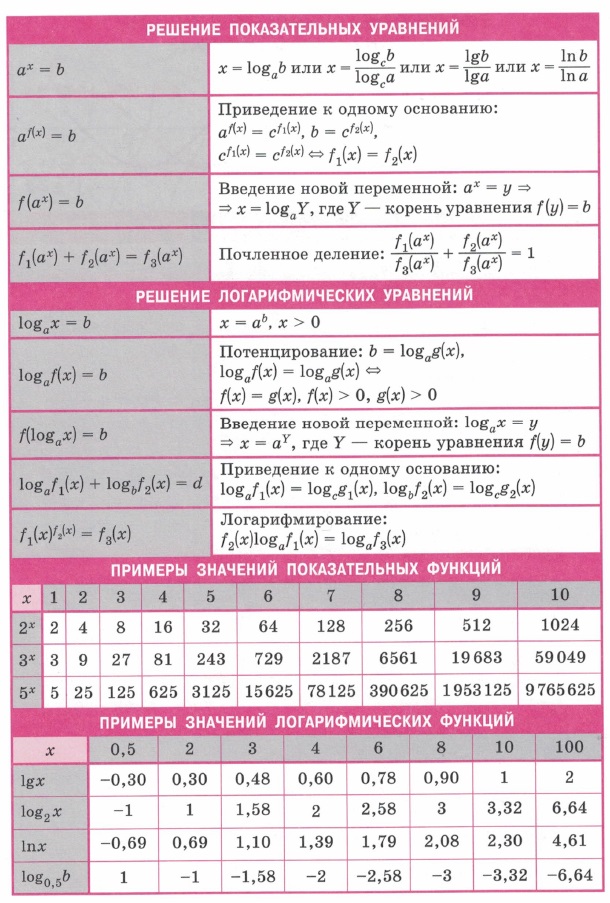
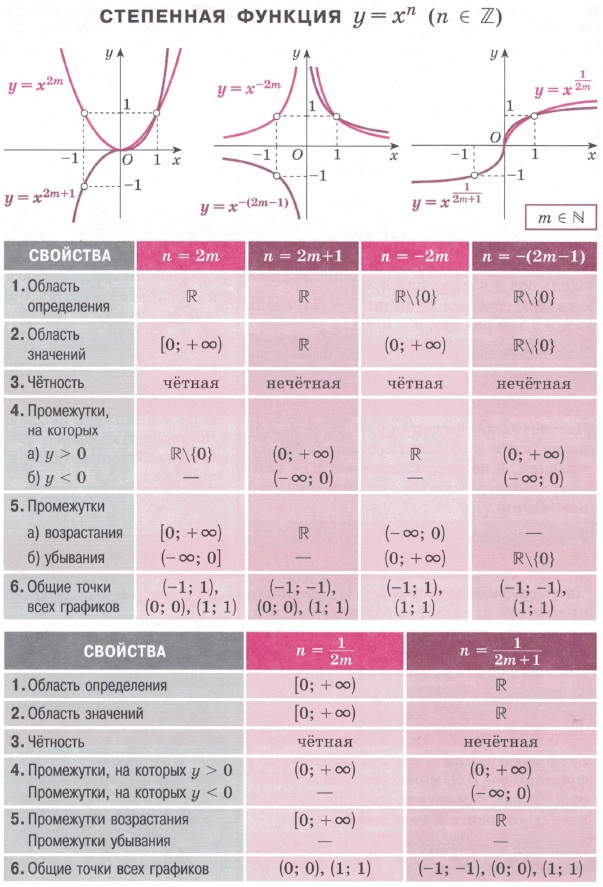
| Квадратичная функция. Область определения / значений. Вершина графика функции. Нули. Свойства степеней. Св-ва арифметических корней. Формулы сокращенного умножения. | Показательная и логарифмическая функция. Область определения / значений. Промежутки знакопостоянства, монотонности, нули. Связь логарифмической и показательной функции. Свойства логарифмов. | Решение показательных уравнений. Решение логарифмических уравнений. Примеры значений логарифмических и показательных функций. | Тригонометрический функции синус и косинус. Область определения / значений. Промежутки знакопостоянства, монотонности, нули. Точки минимума и максимума. Четность, периоды. |
 |  |  |  |
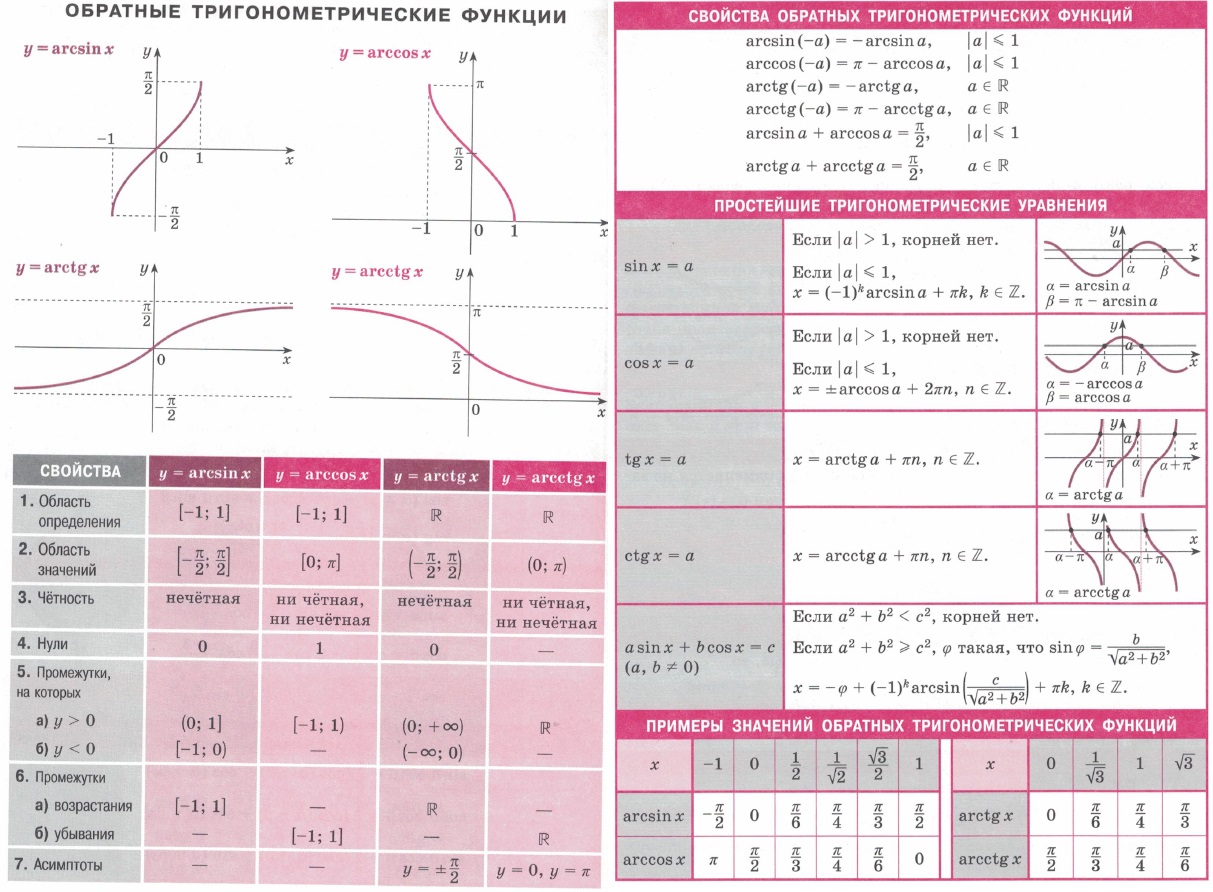
| Обратные тригонометрические функции: arcsin x, arccos x, arctg x, arcctg x, графики, свойства, область определения и значений, асимптоты, промежутки знакопостоянства, возрастания, убывания. Простейшие тригонометрические функции — связь с обратными. Примеры значений обратных тригонометрических функций. | Комбинаторика. Факториал. Перестановки. Размещения. Сочетания. Биноминальные коэффициенты. Треугольник Паскаля. Свойства биноминальных коэффициентов. Формула бинома | ||
 |  |  | |
 |  | ||
| Решение тригонометрических неравенств: sin x > a, sin x a, cos x a, tg x a, ctg x a, cos x a, tg x a, ctg x a, sin x a, cos x a, tg x a, ctg x |  | ||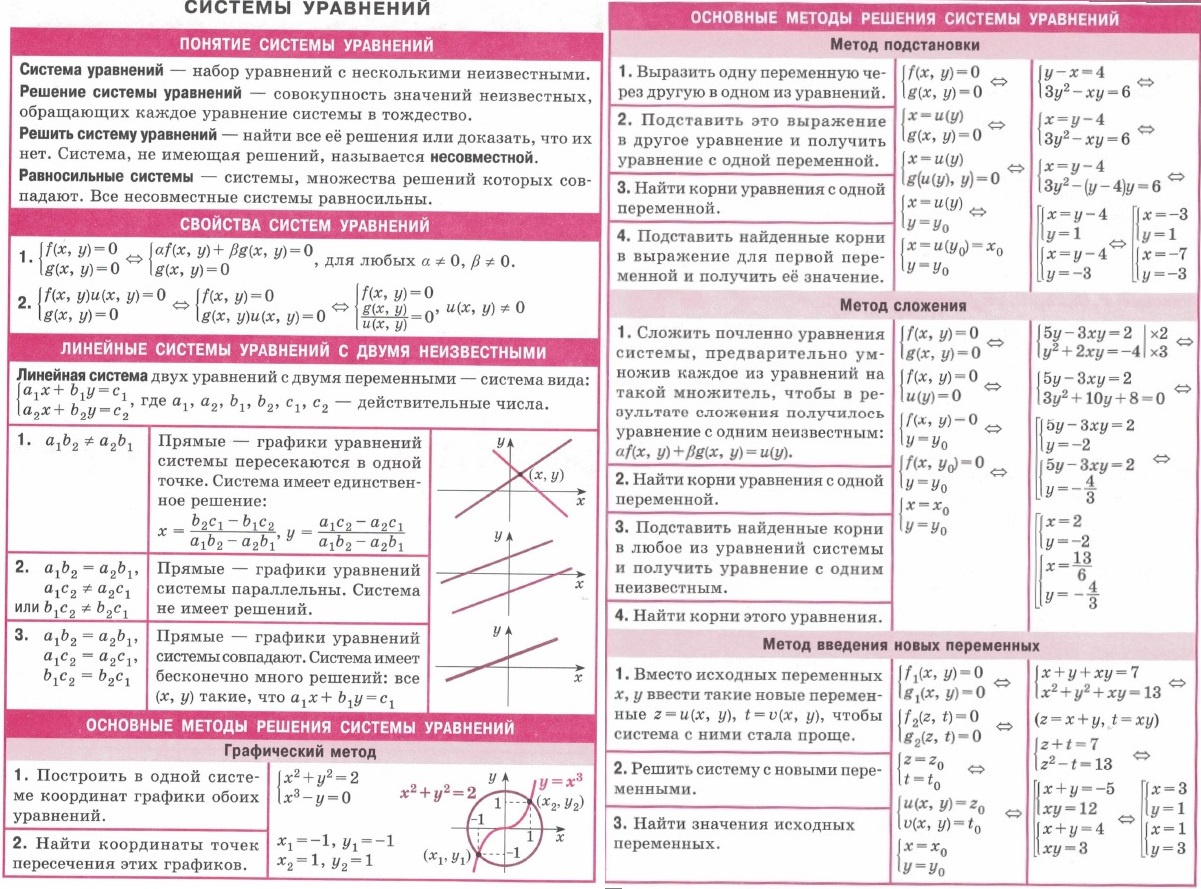
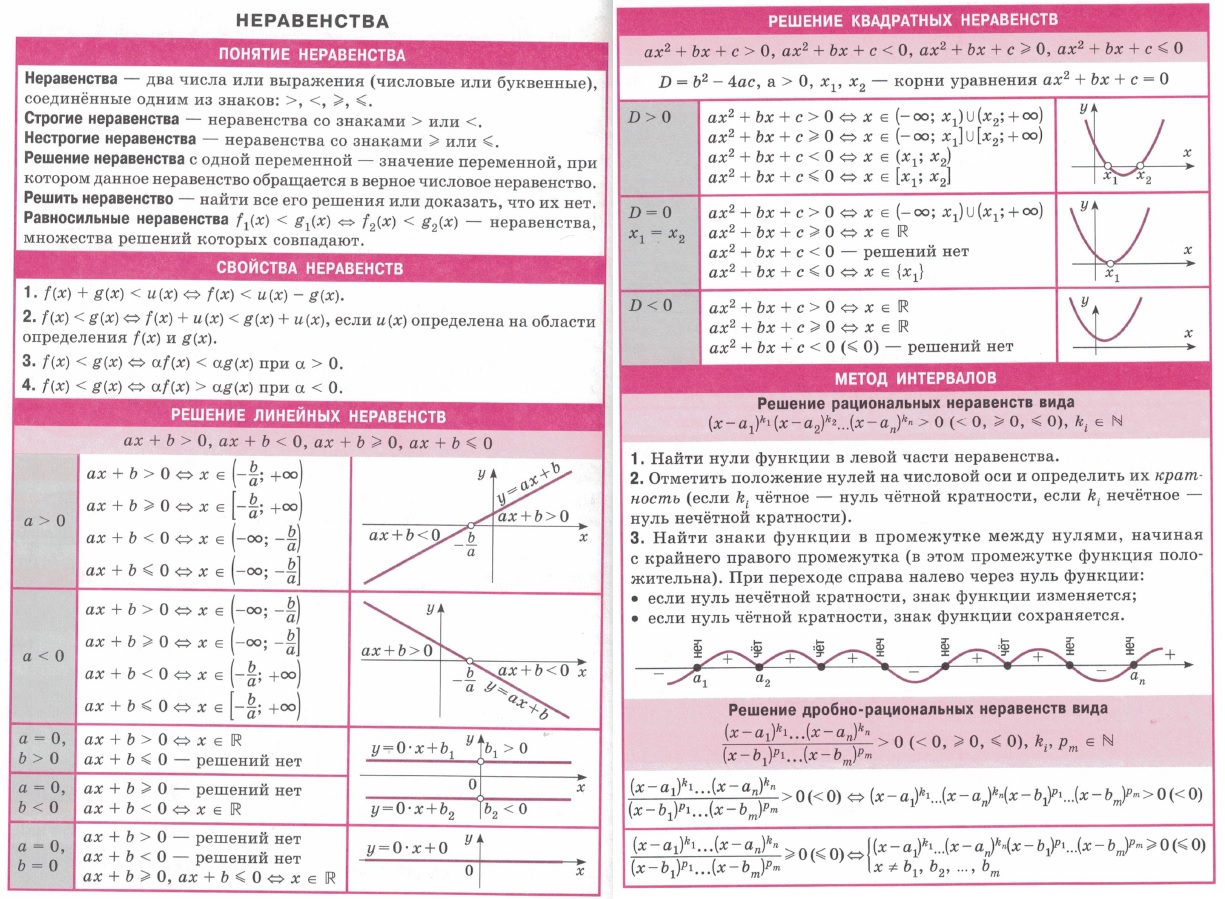
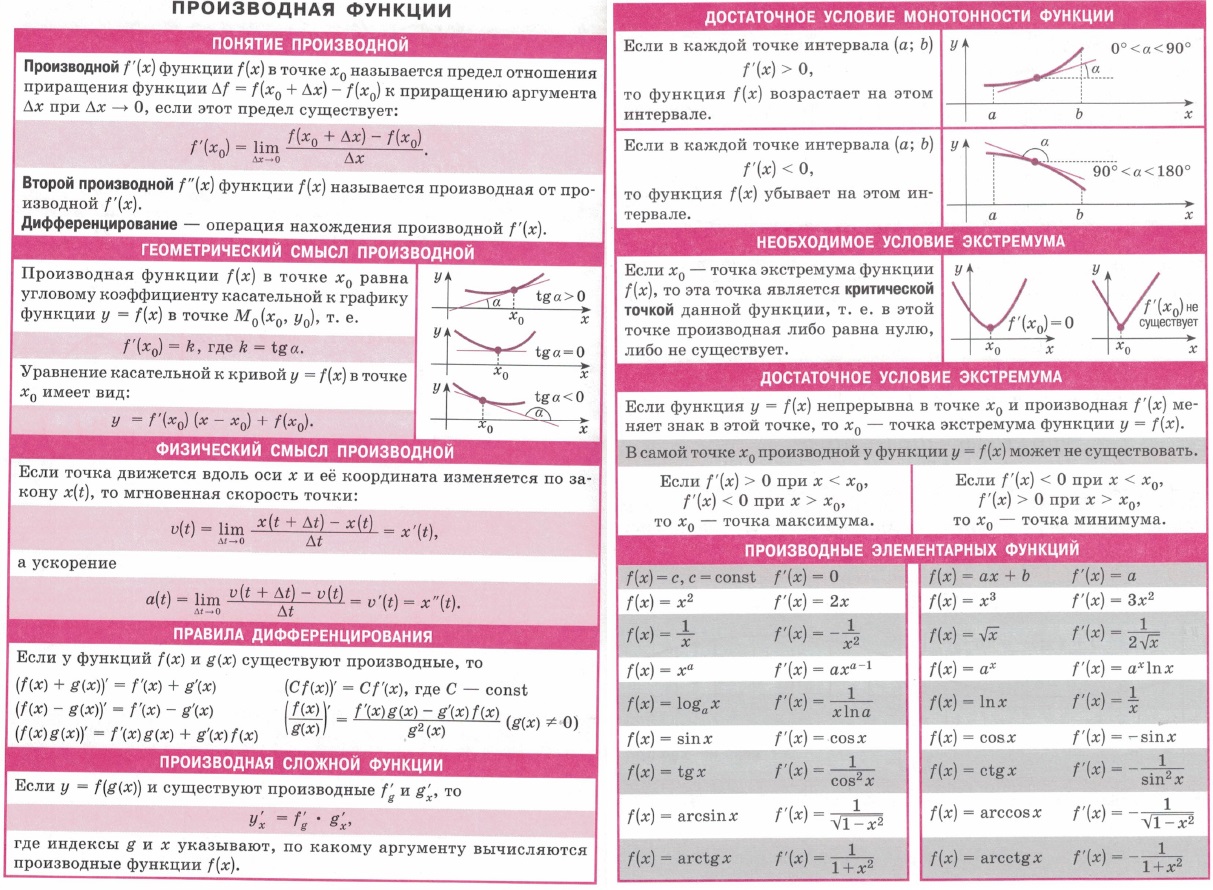
| Производная функции. Определение, вторая производная, дифференцирование, геометрический и физический смысл производной, правила дифференцирования, производная сложной функции, достаточное условие монотонности функции, необходимое и достаточное условия экстремума, производные элементарных функций. | |||
 |  | ||
| Определение комплексного числа. Геометрическая интерпретация комплексного числа. Тригонометрическая форма комплексного числа. Показательная форма комплексного числа. Действия с комплексными числами. Последовательности, пределы последовательности. Теоремы о пределах числовых последовательностей. | Определение предела числовой функции. Односторонние пределы. Свойства пределов. Непрерывные функции и их свойства. Точки разрыва и их классификации. Замечательные пределы. Важные пределы. Теоремы о среднем. Правило Лопиталя. | Линейные пространства. Линейная зависимость и независимость системы векторов. Размерность и базис линейного пространства. Скалярное и векторное произведение векторов. Смешанное произведение векторов. Матрица перехода от базиса к базису. Преобразование координат вектора при переходе к новому базису. Евклидово пространство. Длина вектора. Угол между векторами. Линейные преобразования пространства. Матрица линейного преобразования. Связь между координатами образа и прообраза. | Связь между координатами одного и того же линейного оператора в разных базисах. Угол между прямой и плоскостью. Расстояние от точки до плоскости. Характеристические уравнения линейного оператора. Собственные векторы линейного оператора и их свтойства. Поверхности второго порядка. Плоскость в пространстве. Виды углов в пространстве. Уравнения плоскости. |
| | | |
| Набор 3 — Геометрия. | ||||||||||||||||||||||
| Свойства треугольников, свойства четырехугольников, свойства окружностей, правильные многоугольники. | Прямоугольная декартова система координат. Тела вращения. Цилиндр, конус, усеченный конус, сфера и шар, части шара. Призма. Пирамида. | Различные виды углов. Построение плоских фигур. | Радиальное измерение угловых величин. Свойства треугольников и правильных многоугольников. Выпуклые многоугольники. Подобие. Признаки подобия треугольников. | |||||||||||||||||||
 |  |  |  | |||||||||||||||||||
| Эллипс. Гипербола и ее свойства. Парабола и ее свойства. | Полярная система координат. Цилиндрическая и сферическая системы координат. Двугранный угол. Трехгранный угол. | Свойства четырехугольников. Виды четырехугольников. Свойства произвольных четырехугольников. Свойства параллелограмма. Свойства ромба. Свойства прямоугольника. Свойства квадрата. Свойства трапеции | ||||||||||||||||||||
 |  |  | ||||||||||||||||||||
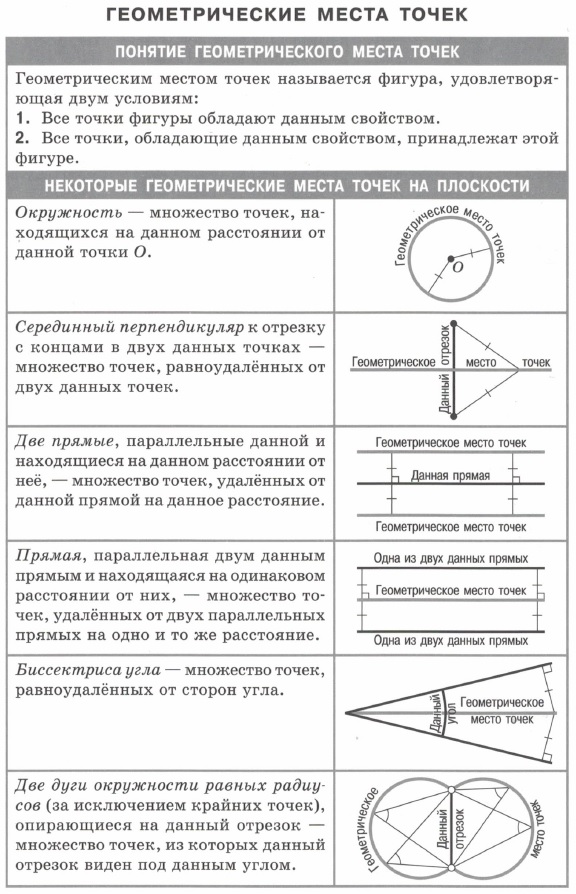
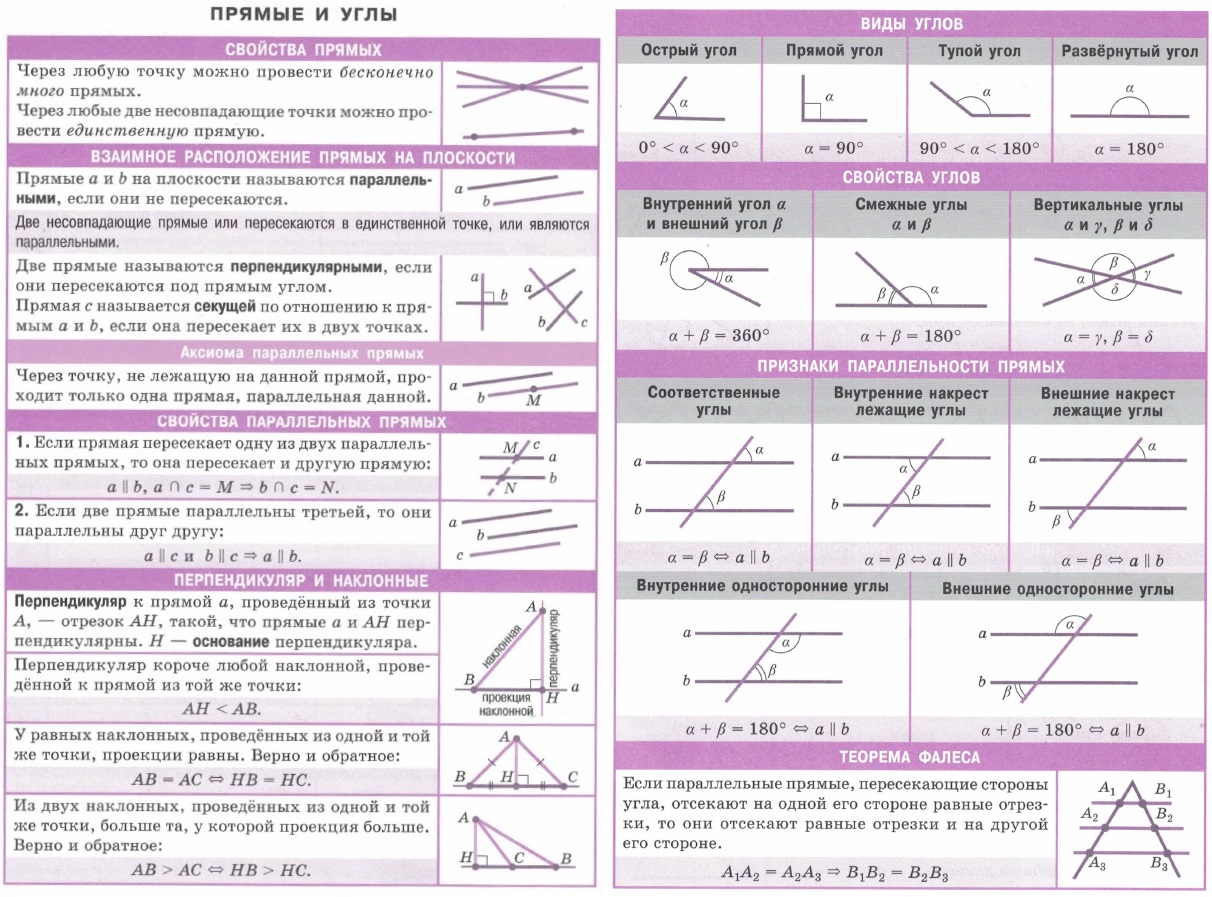
| Геометрические места точек. Понятия. Примеры. | Преобразования фигур. Параллельный перенос. Поворот. Преобразования симметрии относительно точки и прямой. Гомотетия. Подобие. | Прямые и углы. Свойства прямых. Взаимное расположение прямых на плоскости. Аксиома параллельности и свойства параллельных прямых. Перпендикуляр и наклонные. Виды углов, свойства углов, признаки параллельности прямых, Теорема Фалеса. | ||||||||||||||||||||
 |  |  | ||||||||||||||||||||
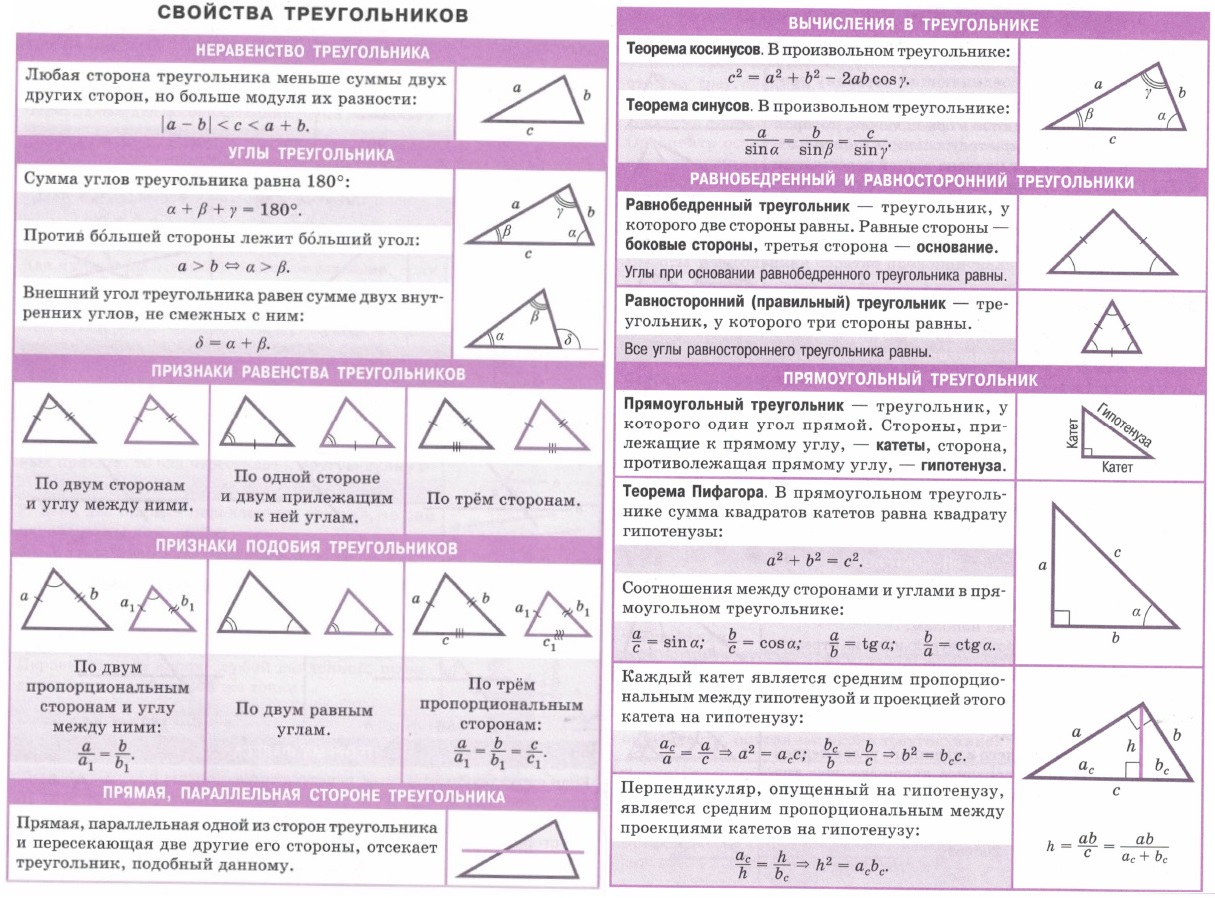
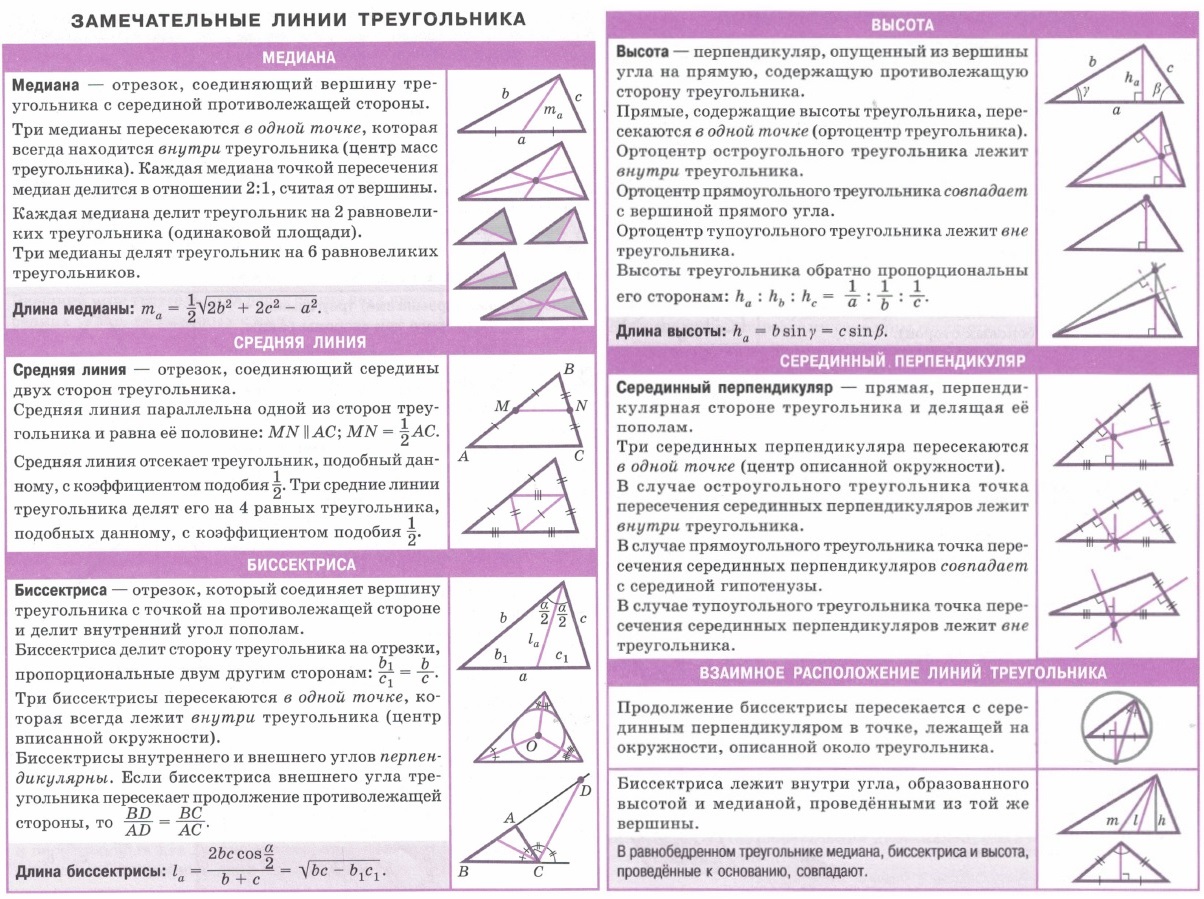
| Свойства треугольников. Неравенство треугольника. Углы треугольника. Признаки подобия треугольников, прямая — параллельная стороне. Вычисления в треугольнике. Равнобедренный, равносторонний и прямоугольный треугольники. | Замечательные линии треугольника. Медиана, средняя линия, биссектриса, высота, серединный перпендикуляр, взаимное расположение линий треугольника. | |||||||||||||||||||||
 |  | |||||||||||||||||||||
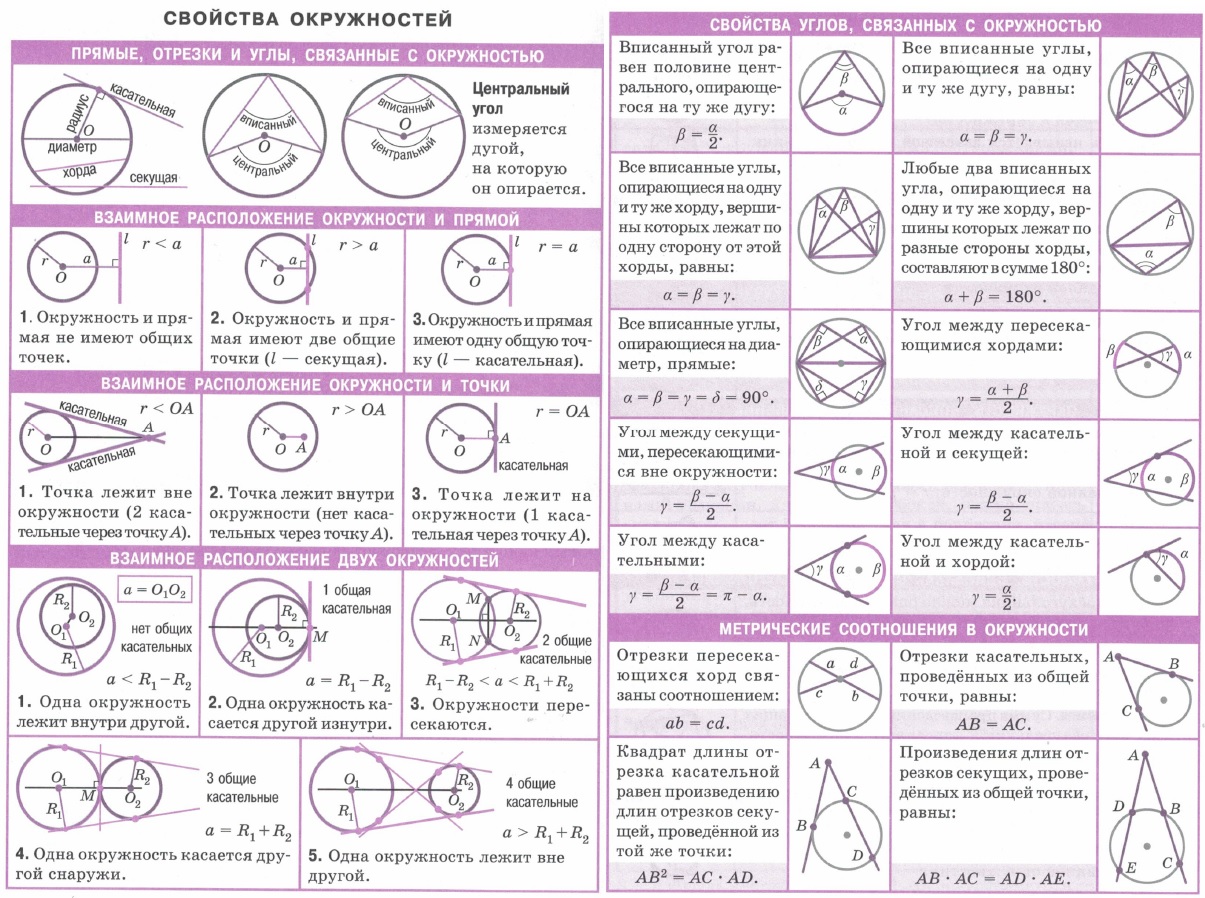
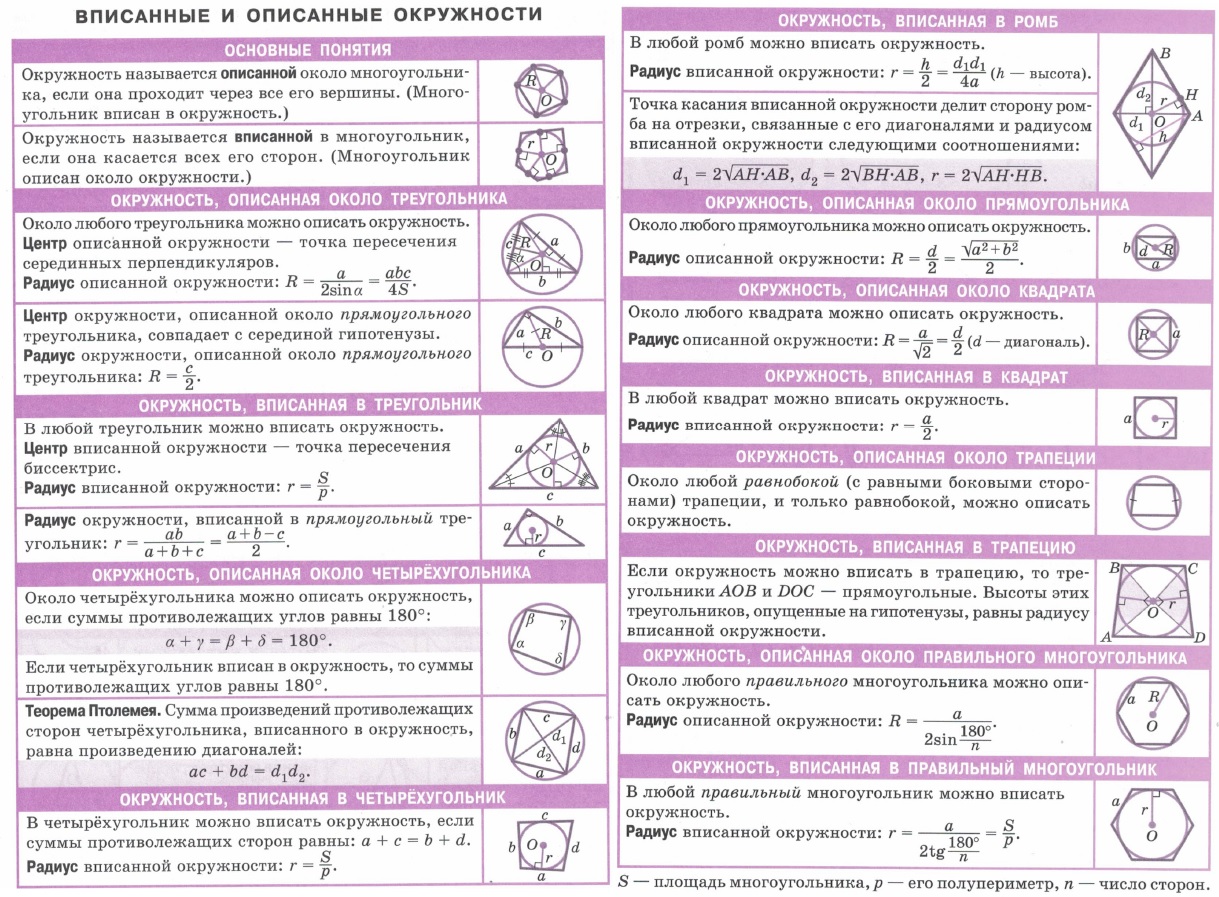
| Свойства окружностей. Прямые, отрезки и углы, связанные с окружностью. Взаимное расположение окружности и прямой, окружности и точки, двух окружностей. Свойства углов, связанных с окружностью. Метрические соотношения в окружности. | Вписанные и описанные окружности. Описанные и вписанные в треугольник, четырехугольник, ромб, прямоугольник, квадрат, трапецию и правильный многоугольник окружности. | |||||||||||||||||||||
 |  | |||||||||||||||||||||
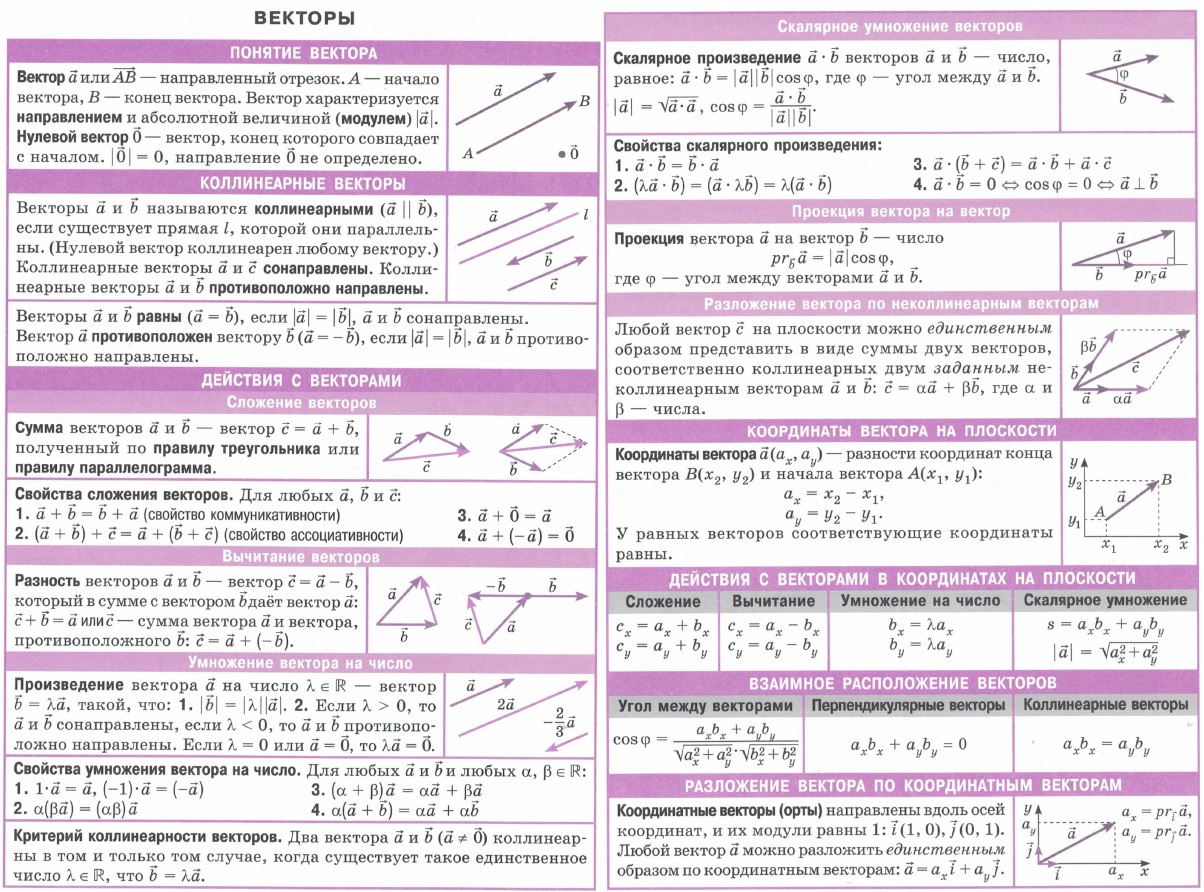
| Понятие вектора. Коллинеарные векторы. Действия с векторами и их свойства — сложение и вычитание векторов, умножение вектора на число, критерий коллинеарности. Скалярное умножение (произведение) векторов. Проекция вектора на вектор. Разложение векторов по неколлинеарным векторам. Координаты вектора на плоскости. Действия с векторами в координатах на плоскости. Взаимное расположение векторов. Разложение вектора по координатным векторам. | Декартовы координаты на плоскости и в пространстве. Координаты точки. Координаты середины отрезка. Расстояние между точками. Уравнение прямой, уравнение плоскости. Уравнение окружности. Уравнение сферы. | |||||||||||||||||||||
 |  | |||||||||||||||||||||
| Прямые и плоскости в пространстве. Параллельность и перпендикулярность прямых и плоскостей. Признаки параллельности прямых и плоскостей. Признаки и свойства прямых перпендикулярных плоскости и перпендикулярных плоскостей. | Перпендикуляр и наклонные. Проекция наклонной, теорема о трех перпендикулярах. Определения и признаки скрещивающихся прямых. Углы в стереометрии (плоские углы в стереометрии) | |||||||||||||||||||||
| Неравенство | Графическое решение | Форма записи ответа | ||||||
|---|---|---|---|---|---|---|---|---|
| x c | x ∈ ( − ∞ ; c ) | |||||||
| x ≤ c | x ∈ ( − ∞ ; c ] | |||||||
| x > c | x ∈ ( c ; + ∞ ) | |||||||
| x ≥ c | Алгоритм решения линейного неравенства
a x b a x ≤ b a x > b a x ≥ b
Примеры решения линейных неравенств: №1. Решить неравенство 3 ( 2 − x ) > 18. Решение: Раскрываем скобки, переносим иксы влево, числа вправо, приводим подобные слагаемые. − 3 x > 18 − 6 − 3 x > 12 | ÷ ( − 3 ) Делим обе части неравенства на ( -3 ) – коэффициент, который стоит перед x . Так как − 3 0 , знак неравенства поменяется на противоположный . x 12 − 3 ⇒ x − 4 Остается записать ответ (см. таблицу числовых промежутков). Ответ: x ∈ ( − ∞ ; − 4 ) №2. Решить неравество 6 x + 4 ≥ 3 ( x + 1 ) − 14. Решение: Раскрываем скобки, переносим иксы влево, числа вправо, приводим подобные слагаемые. 6 x + 4 ≥ 3 x + 3 − 14 6 x − 3 x ≥ 3 − 14 − 4 3 x ≥ − 15 | ÷ 3 Делим обе части неравенства на ( 3 ) – коэффициент, который стоит перед x . Так как 3 > 0, знак неравенства после деления меняться не будет. x ≥ − 15 3 ⇒ x ≥ − 5 Остается записать ответ (см. таблицу числовых промежутков). Особые случаи (в 14 задании ОГЭ 2019 они не встречались, но знать их полезно). №1. Решить неравенство 6 x − 1 ≤ 2 ( 3 x − 0,5 ). Решение: Раскрываем скобки, переносим иксы влево, числа вправо, приводим подобные слагаемые. 6 x − 6 x ≤ − 1 + 1 Получили верное неравенство, которое не зависит от переменной x . Возникает вопрос, какие значения может принимать переменная x , чтобы неравенство выполнялось? Любые! Какое бы значение мы ни взяли, оно все равно сократится и результат неравенства будет верным. Рассмотрим три варианта записи ответа. Ответ:
№2. Решить неравенство x + 3 ( 2 − 3 x ) > − 4 ( 2 x − 12 ). Решение: Раскрываем скобки, переносим иксы влево, числа вправо, приводим подобные слагаемые. x + 6 − 9 x > − 8 x + 48 − 8 x + 8 x > 48 − 6 Получили неверное равенство, которое не зависит от переменной x . Какие бы значения мы ни подставляли в исходное неравенство, результат окажется одним и тем же – неверное неравенство. Ни при каких значениях x исходное неравенство не станет верным. Данное неравенство не имеет решений. Запишем ответ. Квадратные неравенства Квадратные неравенства – это неравенства вида: a x 2 + b x + c > 0 a x 2 + b x + c ≥ 0 a x 2 + b x + c 0 a x 2 + b x + c ≤ 0 где a, b, c — некоторые числа, причем a ≠ 0, x — переменная. Существует универсальный метод решения неравенств степени выше первой (квадратных, кубических, биквадратных и т.д.) – метод интервалов. Если его один раз как следует осмыслить, то проблем с решением любых неравенств не возникнет. Для того, чтобы применять метод интервалов для решения квадратных неравенств, надо уметь хорошо решать квадратные уравнения (см. урок 4). Алгоритм решения квадратного неравенства методом интервалов
Если знак неравенства строгий > , , точки будут выколотые. Если знак неравенства нестрогий ≥ , ≤ , точки будут жирные (заштрихованный).
Если получилось положительное число, знак на интервале плюс. На остальных интервалах знаки будут чередоваться. Точки выколотые, если знак неравенства строгий. Точки жирные, если знак неравенства нестрогий. Если получилось отрицательное число, знак на интервале минус. На остальных интервалах знаки будут чередоваться. Точки выколотые, если знак неравенства строгий. Точки жирные, если знак неравенства нестрогий.
Если знак неравенства > или ≥ в ответ выбираем интервалы со знаком +. Если знак неравенства или ≤ в ответ выбираем интервалы со знаком -. Примеры решения квадратных неравенств: №1. Решить неравенство x 2 ≥ x + 12. Решение: Приводим неравенство к виду a x 2 + b x + c ≥ 0, а затем решаем уравнение a x 2 + b x + c = 0. a = 1, b = − 1, c = − 12 D = b 2 − 4 a c = ( − 1 ) 2 − 4 ⋅ 1 ⋅ ( − 12 ) = 1 + 48 = 49 D > 0 ⇒ будет два различных действительных корня x 1,2 = − b ± D 2 a = − ( − 1 ) ± 49 2 ⋅ 1 = 1 ± 7 2 = [ 1 + 7 2 = 8 2 = 4 1 − 7 2 = − 6 2 = − 3 Наносим точки на ось x . Так как знак неравенства нестрогий, точки будут жирными. Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 6 . Подставляем эту точку в исходное выражение: x 2 − x − 1 = 6 2 − 6 − 1 = 29 > 0 Это значит, что знак на интервале, в котором лежит точка 6 будет +. Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный. В ответ пойдут два интервала. В математике для объединения нескольких интервалов используется знак объединения: ∪ . Точки -3 и 4 будут в квадратных скобках, так как они жирные. Ответ: x ∈ ( − ∞ ; − 3 ] ∪ [ 4 ; + ∞ ) №2. Решить неравенство − 3 x − 2 ≥ x 2 . Решение: Приводим неравенство к виду a x 2 + b x + c ≥ 0, а затем решаем уравнение a x 2 + b x + c = 0. a = − 1, b = − 3, c = − 2 D = b 2 − 4 a c = ( − 3 ) 2 − 4 ⋅ ( − 1 ) ⋅ ( − 2 ) = 9 − 8 = 1 D > 0 ⇒ будет два различных действительных корня x 1,2 = − b ± D 2 a = − ( − 3 ) ± 1 2 ⋅ ( − 1 ) = 3 ± 1 − 2 = [ 3 + 1 − 2 = 4 − 2 = − 2 3 − 1 − 2 = 2 − 2 = − 1 x 1 = − 2, x 2 = − 1 Наносим точки на ось x . Так как знак неравенства нестрогий, точки будут жирными. Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 0 . Подставляем эту точку в исходное выражение: − x 2 − 3 x − 2 = − ( 0 ) 2 − 3 ⋅ 0 − 2 = − 2 0 Это значит, что знак на интервале, в котором лежит точка 0 будет − . Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный. Поскольку знак неравенства ≥ , выбираем в ответ интервал со знаком +. Точки -2 и -1 будут в квадратных скобках, так как они жирные. Ответ: x ∈ [ − 2 ; − 1 ] №3. Решить неравенство 4 x 2 + 3 x . Решение: Приводим неравенство к виду a x 2 + b x + c ≥ 0, а затем решаем уравнение a x 2 + b x + c = 0. a = − 1, b = − 3, c = 4 D = b 2 − 4 a c = ( − 3 ) 2 − 4 ⋅ ( − 1 ) ⋅ 4 = 9 + 16 = 25 D > 0 ⇒ будет два различных действительных корня x 1,2 = − b ± D 2 a = − ( − 3 ) ± 25 2 ⋅ ( − 1 ) = 3 ± 5 − 2 = [ 3 + 5 − 2 = 8 − 2 = − 4 3 − 5 − 2 = − 2 − 2 = 1 Наносим точки на ось x . Так как знак неравенства строгий, точки будут выколотыми. Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 2 . Подставляем эту точку в исходное выражение: − x 2 − 3 x + 4 = − ( 2 ) 2 − 3 ⋅ 2 + 4 = − 6 0 Это значит, что знак на интервале, в котором лежит точка 2 , будет -. Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный. Поскольку знак неравенства , выбираем в ответ интервалы со знаком − . Точки -4 и 1 будут в круглых скобках, так как они выколотые. Ответ: x ∈ ( − ∞ ; − 4 ) ∪ ( 1 ; + ∞ ) №4. Решить неравенство x 2 − 5 x 6. Решение: Приводим неравенство к виду a x 2 + b x + c ≥ 0, а затем решаем уравнение a x 2 + b x + c = 0. a = 1, b = − 5, c = − 6 D = b 2 − 4 a c = ( − 5 ) 2 − 4 ⋅ 1 ⋅ ( − 6 ) = 25 + 25 = 49 D > 0 ⇒ будет два различных действительных корня x 1,2 = − b ± D 2 a = − ( − 5 ) ± 49 2 ⋅ 1 = 5 ± 7 2 = [ 5 + 7 2 = 12 2 = 6 5 − 7 2 = − 2 2 = − 1 Наносим точки на ось x . Так как знак неравенства строгий, точки будут выколотыми. Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 10. Подставляем эту точку в исходное выражение: x 2 − 5 x − 6 = 10 2 − 5 ⋅ 10 − 6 = 100 − 50 − 6 = 44 > 0 Это значит, что знак на интервале, в котором лежит точка 10 будет +. Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный. Поскольку знак неравенства , выбираем в ответ интервал со знаком -. Точки -1 и 6 будут в круглых скобках, так как они выколотые Ответ: x ∈ ( − 1 ; 6 ) №5. Решить неравенство x 2 4. Решение: Переносим 4 в левую часть, раскладываем выражение на множители по ФСУ и находим корни уравнения. ( x − 2 ) ( x + 2 ) = 0 ⇔ [ x − 2 = 0 x + 2 = 0 [ x = 2 x = − 2 Наносим точки на ось x . Так как знак неравенства строгий, точки будут выколотыми. Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 3 . Подставляем эту точку в исходное выражение: x 2 − 4 = 3 2 − 4 = 9 − 4 = 5 > 0 Это значит, что знак на интервале, в котором лежит точка 3 будет +. Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный. Поскольку знак неравенства , выбираем в ответ интервал со знаком − . Точки -2 и 2 будут в круглых скобках, так как они выколотые. Ответ: x ∈ ( − 2 ; 2 ) №6. Решить неравенство x 2 + x ≥ 0. Решение: Выносим общий множитель за скобку, находим корни уравнения x 2 + x = 0. x ( x + 1 ) = 0 ⇔ [ x = 0 x + 1 = 0 [ x = 0 x = − 1 Наносим точки на ось x . Так как знак неравенства нестрогий, точки будут жирными. Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 1 . Подставляем эту точку в исходное выражение: x 2 + x = 1 2 + 1 = 2 > 0 Это значит, что знак на интервале, в котором лежит точка 1 будет +. Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный. Поскольку знак неравенства ≥ , выбираем в ответ интервалы со знаком +. В ответ пойдут два интервала. Точки -1 и 0 будут в квадратных скобках, так как они жирные. Ответ: x ∈ ( − ∞ ; − 1 ] ∪ [ 0 ; + ∞ ) Вот мы и познакомились с методом интервалов. Он нам еще пригодится при решении дробно рациональных неравенств, речь о которых пойдёт ниже. Дробно рациональные неравенства Дробно рациональное неравенство – это неравенство, в котором есть дробь, в знаменателе которой стоит переменная, т.е. неравенство одного из следующих видов: f ( x ) g ( x ) 0 f ( x ) g ( x ) ≤ 0 f ( x ) g ( x ) > 0 f ( x ) g ( x ) ≥ 0 Дробно рациональное неравенство не обязательно сразу выглядит так. Иногда, для приведения его к такому виду, приходится потрудиться (перенести слагаемые в левую часть, привести к общему знаменателю). Примеры дробно рациональных неравенств: x − 1 x + 3 0 3 ( x + 8 ) ≤ 5 x 2 − 1 x > 0 x + 20 x ≥ x + 3 Как же решать эти дробно рациональные неравенства? Да всё при помощи того же всемогущего метода интервалов. Алгоритм решения дробно рациональных неравенств:
f ( x ) g ( x ) 0 f ( x ) g ( x ) ≤ 0 f ( x ) g ( x ) > 0 f ( x ) g ( x ) ≥ 0
В этом пункте алгоритма мы будем делать всё то, что нам запрещали делать все 9 лет обучения в школе – приравнивать знаменатель дроби к нулю. Чтобы как-то оправдать свои буйные действия, полученные точки при нанесении на ось x будем всегда рисовать выколотыми, вне зависимости от того, какой знак неравенства.
Вне зависимости от знака неравенства Если знак неравенства строгий , Если знак неравенства нестрогий ,
Примеры решения дробно рациональных неравенств: №1. Решить неравенство x − 1 x + 3 > 0. Решение: Будем решать данное неравенство в соответствии с алгоритмом.
x = 1 — это ноль числителя . Поскольку знак неравенства строгий, ноль числителя при нанесени на ось x будет выколотым. Запомним это.
x = − 3 — это ноль знаменателя . При нанесении на ось x точка будет всегда выколотой (вне зависимости от знака неравенства) .
При нанесении нулей числителя обращаем внимание на знак неравенства. В данном случае знак неравенства строгий, значит нули числителя будут выколотыми. Ну а нули знаменателя выколоты всегда.
Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 2 . Подставляем эту точку в исходное выражение f ( x ) g ( x ) : x − 1 x + 3 = 2 − 1 2 + 3 = 1 5 > 0, Это значит, что знак на интервале, в котором лежит точка 2 будет +. Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный.
Поскольку знак неравенства > , выбираем в ответ интервалы со знаком +. В ответ пойдут два интервала. Точки -3 и 1 будут в круглых скобках, так как обе они выколотые. Ответ: x ∈ ( − ∞ ; − 3 ) ∪ ( 1 ; + ∞ ) №2. Решить неравенство 3 ( x + 8 ) ≤ 5. Решение: Будем решать данное неравенство в соответствии с алгоритмом.
3 ( x + 8 ) − 5 x + 8 ≤ 0 3 x + 8 − 5 ( x + 8 ) x + 8 ≤ 0 3 − 5 ( x + 8 ) x + 8 ≤ 0 3 − 5 x − 40 x + 8 ≤ 0 − 5 x − 37 x + 8 ≤ 0
x = − 37 5 = − 37 5 = − 7,4 x = − 7,4 — ноль числителя . Поскольку знак неравенства нестрогий, при нанесении этой точки на ось x точка будет жирной.
x = − 8 — это ноль знаменателя . При нанесении на ось x , точка будет всегда выколотой (вне зависимости от знака неравенства).
При нанесении нулей числителя обращаем внимание на знак неравенства. В данному случае знак неравенства нестрогий, значит нули числителя будут жирными. Ну а нули знаменателя выколоты всегда.
Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 0 . Подставляем эту точку в исходное выражение f ( x ) g ( x ) : − 5 x − 37 x + 8 = − 5 ⋅ 0 − 37 0 + 8 = − 37 8 0 Это значит, что знак на интервале, в котором лежит точка 0 будет -. Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный.
Поскольку знак неравенства ≤ , выбираем в ответ интервалы со знаком -. В ответ пойдут два интервала. Точка -8 будет в круглой скобке, так как она выколотая, точка -7,4 будет в квадратных скобках, так как она жирная. Ответ: x ∈ ( − ∞ ; − 8 ) ∪ [ − 7,4 ; + ∞ ) №3. Решить неравенство x 2 − 1 x > 0. Решение: Будем решать данное неравенство в соответствии с алгоритмом.
( x − 1 ) ( x + 1 ) = 0 ⇒ [ x − 1 = 0 x + 1 = 0 [ x = 1 x = − 1 x 1 = 1, x 2 = − 1 — нули числителя . Поскольку знак неравенства строгий, при нанесении этих точек на ось x точки будут выколотыми.
x = 0 — это ноль знаменателя . При нанесении на ось x , точка будет всегда выколотой (вне зависимости от знака неравенства).
При нанесении нулей числителя обращаем внимание на знак неравенства. В данному случае знак неравенства строгий, значит нули числителя будут выколотыми. Ну а нули знаменателя и так выколоты всегда.
Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 2 . Подставляем эту точку в исходное выражение f ( x ) g ( x ) : x 2 − 1 x = 2 2 − 1 2 = 4 − 1 2 = 3 2 > 0, Это значит, что знак на интервале, в котором лежит точка 2, будет +. Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный.
Поскольку знак неравенства > , выбираем в ответ интервалы со знаком +. В ответ пойдут два интервала. Все точки будут в круглых скобках, так как они выколотые. Ответ: x ∈ ( − 1 ; 0 ) ∪ ( 1 ; + ∞ ) Системы неравенств Системой неравенств называют два неравенства с одной неизвестной, которые объединены в общую систему фигурной скобкой. Пример системы неравенств: Алгоритм решения системы неравенств
Примеры решений систем неравенств: №1. Решить систему неравенств < 2 x − 3 ≤ 5 7 − 3 x ≤ 1 Решение: Будем решать данную систему неравенств в соответствии с алгоритмом.
2 x ≤ 8 | ÷ 2 , поскольку 2 > 0, знак неравенства после деления сохраняется. Точка 4 на графике жирная, так как знак неравенства нестрогий.
− 3 x ≤ − 6 | ÷ ( − 3 ), поскольку − 3 0, знак неравенства после деления меняется на противоположный. Графическая интерпретация решения: Точка 2 на графике жирная, так как знак неравенства нестрогий.
Пересечение решений наблюдается на отрезке от 2 до 4 . Точки 2 и 4 в ответе буду в квадратных скобках, так как обе они жирные. №2. Решить систему неравенств < 2 x − 1 ≤ 5 1 − 3 x − 2 Решение: Будем решать данную систему неравенств в соответствии с алгоритмом.
2 x ≤ 6 | ÷ 2 , поскольку 2 > 0, знак неравенства после деления сохраняется. Точка 3 на графике жирная, так как знак неравенства нестрогий.
3 x − 3 | ÷ 3 , поскольку 3 > 0, знак неравенства после деления сохраняется. Графическая интерпретация решения: Точка -1 на графике выколотая, так как знак неравенства строгий.
Пересечение решений наблюдается на самом левом участке. Точка -1 будет в ответе в круглых скобках, так как она выколотая. Ответ: x ∈ ( − ∞ ; − 1 ) №3. Решить систему неравенств 5 − x Решение: Будем решать данную систему неравенств в соответствии с алгоритмом.
Графическая интерпретация решения:
2 x > 12 | ÷ 2 , поскольку 2 > 0, знак неравенства после деления сохраняется. Графическая интерпретация решения:
Пересечений решений не наблюдается. Значит у данной системы неравенств нет решений. №4. Решить систему неравенств 0 2 x + 3 ≤ x 2 Решение: Будем решать данную систему неравенств в соответствии с алгоритмом.
Графическая интерпретация решения первого неравенства:
Решаем методом интервалов. a = − 1, b = 2, c = 3 D = b 2 − 4 a c = 2 2 − 4 ⋅ ( − 1 ) ⋅ 3 = 4 + 12 = 16 D > 0 — два различных действительных корня. x 1,2 = − b ± D 2 a = − 2 ± 16 2 ⋅ ( − 1 ) = − 2 ± 4 − 2 = [ − 2 − 4 − 2 = − 6 − 2 = 3 − 2 + 4 − 2 = 2 − 2 = − 1 Наносим точки на ось x и расставляем знаки на интервалах. Поскольку знак неравенства нестрогий, обе точки будут заштрихованными. Графическая интерпретация решения второго неравенства:
Пересечение решений наблюдается в двух интервалах. Для того, чтобы в ответе объединить два интервала, используется знак объединения ∪ . Точка -4 будет в круглой скобке, так как она выколотая, а точки -1 и 3 в квадратных, так как они жирные. Видео:Алгебра 10 класс (Урок№19 - Равносильные уравнения и неравенства.)Скачать  Линейные уравнения и неравенства
Видео:Реакция на результаты ЕГЭ 2022 по русскому языкуСкачать  Линейные уравненияЛинейным уравнением относительно переменной x называется уравнение первой степени
где k и b – произвольные вещественные числа. В случае
В случае, когда В случае, когда k = 0, b = 0, решением уравнения (1) является любое число
Видео:Подготовка к ОГЭ . Рациональные неравенства | Математика | TutorOnlineСкачать  Линейные неравенстваЛинейным неравенством относительно переменной x называется неравенство, принадлежащее к одному из следующих типов:
где k и b – произвольные вещественные числа. Решая линейные, да и не только линейные, неравенства, следует помнить, что
В соответствии с этим решение линейных неравенств, в зависимости от значений коэффициентов k и b, представлено в следующей Таблице 1. Таблица 1. – Решение неравенств первой степени (линейных неравенств) 📸 ВидеоКак понять неравенства? Квадратные неравенства. Линейные и сложные неравенства | TutorOnlineСкачать  ШПАРГАЛКИ НА ЕГЭ | #обществознание #егэ #огэ #репетиторСкачать  11 класс, 30 урок, Уравнения и неравенства со знаком радикалаСкачать  ЛИНЕЙНЫЕ УРАВНЕНИЯ - Как решать линейные уравнения // Подготовка к ЕГЭ по МатематикеСкачать  Алгебра 10 класс (Урок№20 - Иррациональные уравнения и неравенства.)Скачать  Как решать неравенства? Часть 1| МатематикаСкачать  Удалили с экзамена ОГЭ Устное Собеседование shorts #shortsСкачать  Решение неравенства методом интерваловСкачать  11 класс, 29 урок, Уравнения и неравенства с модулямиСкачать  Как решать неравенства? 9 - 11 класс. Вебинар | Математика TutorOnlineСкачать  Урок 10. Сложные уравнения и неравенства. Решение уравнений высоких степеней. Вебинар | МатематикаСкачать  Модуль в математике. Уравнения и неравенства | Математика ЕГЭ | УмскулСкачать  СУПЕР ЛАЙФХАК — Как решать Иррациональные УравненияСкачать  Шпаргалка перед ЕГЭ. Профильная математикаСкачать  |
Линейные уравнения
уравнение (1) имеет единственное решение при любом значении b :
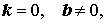уравнение (1) решений не имеет.
