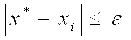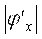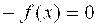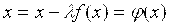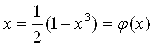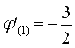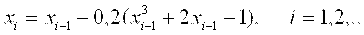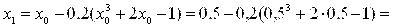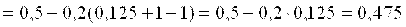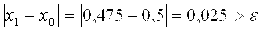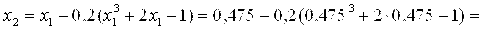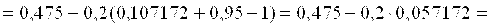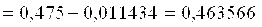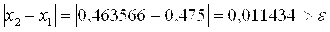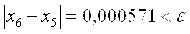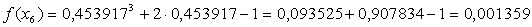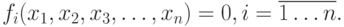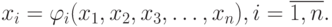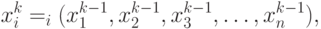Многие практические задачи сводятся к решению системы нелинейных уравнений [2, 6, 10, 12].
Пусть для вычисления неизвестных Х, х2, . х„ требуется решить систему п нелинейных уравнений:
В отличие от систем линейных уравнений не существует прямых методов решения нелинейных систем общего вида. Лишь в некоторых случаях систему (4.1) можно решить непосредственно. Например, для случая двух уравнений иногда удается выразить одно неизвестное через другое и таким образом свести задачу к решению одного нелинейного уравнения относительно одного неизвестного. Для решения систем нелинейных уравнений обычно используют итерационные методы. Рассмотрим два из них — метод простой итерации и метод Ньютона.
Видео:1 3 Решение нелинейных уравнений методом простых итерацийСкачать

Метод простой итерации
Систему уравнений (4.1) представим в следующем виде:
Запишем систему (4.2) в векторной форме: 
Для нахождения вектора корня х* = (х*,х*. х*) уравнения (4.3) часто удобно использовать метод итерации:
где начальное приближение х (0) * х*. Это грубое значение искомого корня. Заметим, что если процесс итерации (4.5) сходится, то предельное значение
обязательно является корнем уравнения (4.3). Действительно, предполагая, что соотношение (4.6) выполнено, и переходя к пределу в равенстве (4.5) прир—>оо, в силу непрерывности функции ф(х) будем иметь:
Таким образом, ?> есть корень векторного уравнения (4.3).
Рассмотрим метод простой итерации на примере системы двух нелинейных уравнений с двумя неизвестными:
Решением системы (4.7) для хе [о, Ь] и ye [с, d будут такие значения х* и у*, которые обращают эту систему в тождество. Необходимо найти х* и у* с заданной степенью точности е.
Запишем систему (4.7) в эквивалентной форме:
Последовательные приближения будут вычисляться по формулам:
где х0, уо — начальные приближения значения искомого корня.
Итерационный процесс можно считать законченным, как только выполнится неравенство
Для определения сходимости процесса имеет место следующая теорема.
Теорема. Пусть в некоторой заданной области хе[а, Ь] и ye[c,d] имеется единственное решение х*, у* системы (4.8) тогда, если:
- • ф)(х,у) и ф2(х, у) определены и непрерывно дифференцируемы в заданной области;
- • начальные приближения х0, у0и все последующие приближения х,„у„ принадлежат заданной области;
- • в рассматриваемой области выполняются неравенства:
то процесс последовательных приближений (4.9) сходится к решению системы уравнений (4.11).
Пр имер 4.1. Методом итерации приближенно решить систему 
Из графического построения (см. рис. 4.1) видно, что система имеет два решения, отличающиеся только знаком.
Ограничимся нахождением положительного решения. Из чертежа видим, что за начальное приближение положительного решения системы можно принять

Рис. 4.1. Отделение корней системы нелинейных уравнений Полагая
Аналогично,
Точное решение системы Х = 0,8261, х2 = 0,5636.
Блок-схема метода итераций приведена на рис. 4.2. Имеют место следующие обозначения неравенств (4.11):
Видео:Метод простых итераций пример решения нелинейных уравненийСкачать

3.2.1. Метод простых итераций (метод последовательных приближений)
Метод реализует стратегию постепенного уточнения значения корня.
Постановка задачи. Дано нелинейное уравнение (3.1). Корень отделен x* Î [a;b]. Требуется уточнить корень с точностью ε.
Уравнение ( 3.1) преобразуем к эквивалентному виду x=φ(x), (3.7)
Что можно сделать всегда и притом множеством способов.
Выберем начальное приближение x0Î [a;b].
Вычислим новые приближения:
Xi=φ(xi-1) , i=1,2,… где i − номер итерации. (3.8)
Последовательное вычисление значений xi по формуле (3.8) называется итерационным процессом метода простых итераций, а сама формула — формулой итерационного процесса метода.
Если 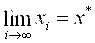
Условие сходимости 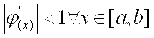
Точное решение x* получить невозможно, так как требуется Бесконечный Итерационный процесс.
Можно получить Приближенное Решение, прервав итерационный (3.8) при достижении условия
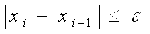
Где ε — заданная точность; i — номер последней итерации.
В большинстве случаев условие завершения итерационного процесса (3.10) обеспечивает близость значения xi к точному решению:
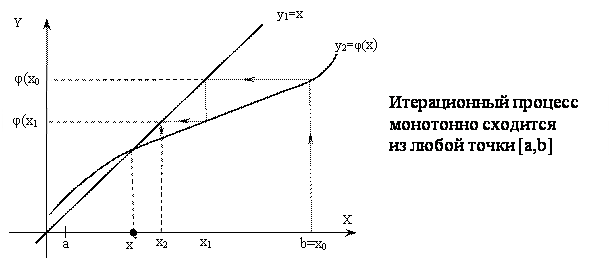
Рассмотрим геометрическую иллюстрацию метода простых итераций.
Уравнение (3.7) представим на графике в виде двух функций: y1 = x и y2= φ(x).
Возможные случаи взаимного расположения графиков функций, и соответственно, видов итерационного процесса показаны на рис. 3.7 – 3.10.
Рис. 3.7 Итерационный процесс для случая 0 1 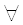
 |
Рис. 3.10 Итерационный процесс для случая 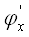
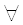
Из анализа графиков следует, что скорость сходимости растет при уменьшении значения
Метод достаточно прост, обобщается на системы уравнений, устойчив к погрешности округления (она не накапливается).
При разработке алгоритма решения нелинейного уравнения методом простых итераций следует предусмотреть защиту итерационного процесса от зацикливания: использовать в качестве дополнительного условия завершения итерационного процесса превышение заданного максимального числа итераций.
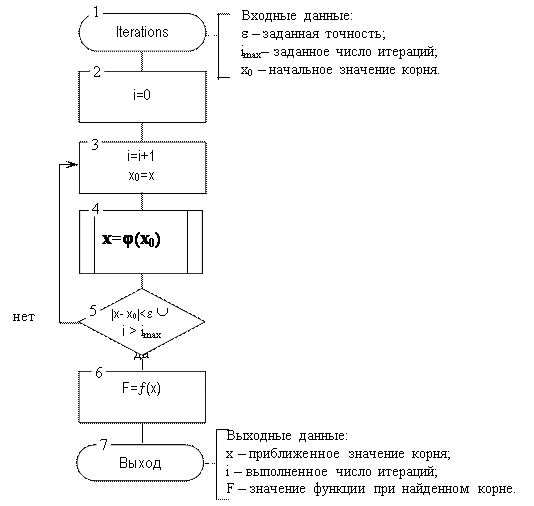 |
Рис 3.11. Алгоритм решения нелинейного уравнения методом
простых итераций:
Основной проблемой применения метода является обеспечение сходимости итерационного процесса: нужно найти такое эквивалентное преобразование (3.1) в (3.7), чтобы обеспечивалось условие сходимости (3.9) .
Простейшие эквивалентные преобразования, например:
F(x) = 0 => x+f(x) = x, т. е. φ(x) = x + f(x)
Или выразить явно x из (3.1)
F(x) = 0 => x — φ(x) = 0 => x = φ(x)
Не гарантируют сходимость.
Рекомендуется следующий способ получения формулы Сходящегося итерационного процесса.
Пусть 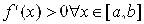
Если это не так, переписать уравнение (3.1) в виде
Умножить обе части уравнения на 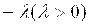
Константу l вычислить по формуле:
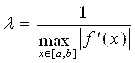
Такое значение λ гарантирует сходящийся итерационный процесс по формуле
Xi = xi+1− λ f(x) (3.12)
Где i=1,2,… — номер итерации, x0Î[a, b] – начальное приближение.
Методом простых итераций уточнить корень уравнения x3=1-2 x с точностью ε=0,001. Корень отделен ранее (см. пример 3.1), x* Î [0;1].
Сначала нужно получить формулу сходящегося итерационного процесса.
Из уравнения выразим явно x:
Проверим условия сходимости для полученной формулы:
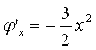
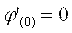
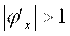
Условие сходимости не соблюдается, полученная формула не позволит уточнить корень.
Воспользуемся описанным выше способом получения формулы итерационного процесса (формулы 3.11, 3.12).
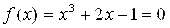
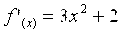
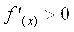
Наибольшее значение 
Следовательно 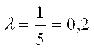
Формула Сходящегося итерационного процесса
Уточним корень с помощью данной формулы.
Выберем начальное приближение на [0;1], например x0=0,5 (середина отрезка).
Вычислим первое приближение
Проверим условие завершения итерационного процесса
Расчет следует продолжить.
X6 = 0,453917 − ответ, т. к.
Проверим полученное значение, подставив в исходное уравнение:
Значение f(x) близко к 0 с точностью, близкой к ε, следовательно, корень уточнен правильно.
Видео:Метод простой итерации Пример РешенияСкачать

Моделирование многомерных нелинейных систем.
В задачах проектирования и исследования поведения реальных объектов, процессов и систем (ОПС) математические модели должны отображать реальные физические нелинейные процессы. При этом эти процессы зависят, как правило, от многих переменных.
В результате математические модели реальных ОПС описываются системами нелинейных уравнений .
Решение систем нелинейных уравнений
Дана система нелинейных уравнений
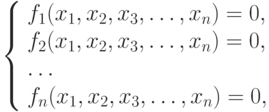 | ( 10.1) |
Необходимо решить эту систему, т.е. найти вектор 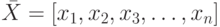

Вектор 

В отличие от систем линейных уравнений для систем нелинейных уравнений неизвестны прямые методы решения. При решении систем нелинейных уравнений используются итерационные методы. Эффективность всех итерационных методов зависит от выбора начального приближения (начальной точки), т.е. вектора 
Область, в которой начальное приближение 

Выбор начальной точки 
Метод простых итераций
Для применения этого метода исходная система (10.1) должна быть преобразована к виду
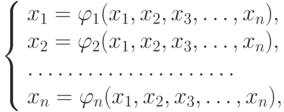 | ( 10.2) |
Далее, выбрав начальное приближение 
т.е. на каждом k-ом шаге поиска вектор переменных 
Итерационный процесс поиска прекращается как только выполнится условие
 | ( 10.3) |
При этом условие (10.3) должно выполняться одновременно по всем переменным.
Метод простых итераций используется для решения таких систем линейных уравнений, в которых выполняется условие сходимости итерационного процесса поиска, а именно:
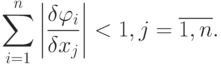 | ( 10.4) |
т.е. сумма абсолютных величин частных производных всех преобразованных уравнений системы (10.2) по j-ой переменной меньше единицы.
На рисунке 10.1 представлена схема алгоритма решения систем нелинейных уравнений методом простых итераций .
🎬 Видео
2.2 Итерационные методы решения СЛАУ (Якоби, Зейделя, релаксации)Скачать

Решение нелинейного уравнения методом простых итераций (программа)Скачать

4.2 Решение систем нелинейных уравнений. МетодыСкачать

10 Численные методы решения нелинейных уравненийСкачать

8 Метод простой итерации Ручной счет Решение системы линейных уравнений СЛАУСкачать

Метод Зейделя Пример РешенияСкачать

Метод Ньютона (метод касательных) Пример РешенияСкачать

Решение систем линейных уравнений методом простой итерации в ExcelСкачать

Решение систем линейных уравнений, урок 5/5. Итерационные методыСкачать

Метод итерацийСкачать

МЗЭ 2021 Лекция 11 Метод Ньютона для решения систем нелинейных уравненийСкачать

Способы решения систем нелинейных уравнений. 9 класс.Скачать

Решение слау методом итераций. Метод простых итераций c++.Скачать

Решение системы линейных уравнений методом простых итераций в MS ExcelСкачать

5 Метод простой итерации Calc Excel Решение системы линейных уравнений СЛАУСкачать

Алгоритмы С#. Метод простых итерацийСкачать

Решение системы линейных уравнений методом итерацийСкачать