Схема алгоритма решения линейного уравнения

Видео:Урок 7 ЛИНЕЙНОЕ УРАВНЕНИЕ С ОДНОЙ ПЕРЕМЕННОЙСкачать

Алгоритмы. Разработка алгоритма решения задачи

Исключительно важно использовать язык блок-схем при разработке алгоритма решения задачи. Решение одной и той же задачи может быть реализовано с помощью различных алгоритмов, отличающихся друг от друга как по времени счета и объему вычислений, так и по своей сложности. Запись этих алгоритмов с помощью блок-схем позволяет сравнивать их, выбирать наилучший алгоритм, упрощать, находить и устранять ошибки.

Отказ от языка блок-схем при разработке алгоритма и разработка алгоритма сразу на языке программирования приводит к значительным потерям времени, к выбору неоптимального алгоритма. Поэтому необходимо изначально разработать алгоритм решения задачи на языке блок-схем, после чего алгоритм перевести на язык программирования.

При разработке алгоритма сложной задачи используется метод пошаговой детализации. На первом шаге продумывается общая структура алгоритма без детальной проработки отдельных его частей. Блоки, требующие детализации, обводятся пунктирной линией и на последующих шагах разработки алгоритма продумываются и детализируются.

В процессе разработки алгоритма решения задачи можно выделить следующие этапы:

• Этап 1 . Математическое описание решения задачи.
• Этап 2 . Определение входных и выходных данных.
• Этап 3 . Разработка алгоритма решения задачи.

Видео:ЛИНЕЙНЫЕ УРАВНЕНИЯ - Как решать линейные уравнения // Подготовка к ЕГЭ по МатематикеСкачать

Базовые алгоритмические конструкции

В теории программирования доказано, что для записи любого, сколь угодно сложного алгоритма достаточно трех базовых структур:

• следование (линейный алгоритм);
• ветвление (разветвляющийся алгоритм);
• цикл-пока (циклический алгоритм).

Линейные алгоритмы

Линейный алгоритм образуется из последовательности действий, следующих одно за другим. Например, для определения площади прямоугольника необходимо сначала задать длину первой стороны, затем задать длину второй стороны, а уже затем по формуле вычислить его площадь.

Пример

ЗАДАЧА. Разработать алгоритм вычисления гипотенузы прямоугольного треугольника по известным значениям длин его катетов a и b.

На примере данной задачи рассмотрим все три этапа разработки алгоритма решения задачи:

Этап 1. Математическое описание решения задачи.

Математическим решением задачи является известная формула:

,

где с-длина гипотенузы, a, b – длины катетов.

Этап 2. Определение входных и выходных данных.

Входными данными являются значения катетов a и b. Выходными данными является длина гипотенузы – c.

Этап 3. Разработка алгоритма решения задачи.

На данной схеме цифрами указаны номера элементов алгоритма, которые соответствуют номерам пунктов словесного описания алгоритма.

Разветвляющиеся алгоритмы

Алгоритм ветвления содержит условие, в зависимости от которого выполняется та или иная последовательность действий.

Пример

ЗАДАЧА. Разработать алгоритм вычисления наибольшего числа из двух чисел x и y.

Этап 1. Математическое описание решения задачи.

Из курса математики известно, если x > y, то наибольшее число x, если x y, то переход к шагу 6, иначе к шагу 7.

В схеме алгоритма решения задачи цифрами указаны номера элементов алгоритма, которые соответствуют номерам шагов словесного описания алгоритма

В рассматриваемом алгоритме (рис.3) имеются три ветви решения задачи:

• первая: это элементы 1, 2, 3, 4, 8.
• вторая: это элементы 1, 2, 3, 5, 6, 8
• третья: это элементы 1, 2, 3, 5, 7, 8.

Выбор ветви определяется значениями x и y в элементах 3 и 5, которые являются условиями, определяющими порядок выполнения элементов алгоритма. Если условие (равенство), записанное внутри символа «решение», выполняется при введенных значениях x и y, то следующими выполняется элементы 4 и 8. Это следует из того, что они соединены линией с надписью «да» и направление (последовательность) вычислений обозначена стрелочкой.

Если условие в элементе 3 не выполняется, то следующим выполняется элемент 5. Он соединен с элементом 3 линией с надписью «нет». Если условие, записанное в элементе 5, выполняется, то выполняется элементы 6 и 8, в противном случае выполняются элементы 7 и 8.

Циклические алгоритмы

Циклический алгоритм – определяет повторение некоторой части действий (операций), пока не будет нарушено условие, выполнение которого проверяется в начале цикла. Совокупность операций, выполняемых многократно, называется телом цикла.

Алгоритмы, отдельные действия в которых многократно повторяются, называются циклическими алгоритмами, Совокупность действий, связанную с повторениями, называют циклом.

При разработке алгоритма циклической структуры выделяют следующие понятия:

• параметр цикла – величина, с изменением значения которой связано многократное выполнение цикла;
• начальное и конечное значения параметров цикла;
• шаг цикла – значение, на которое изменяется параметр цикла при каждом повторении.

Цикл организован по определенным правилам. Циклический алгоритм состоит из подготовки цикла, тела цикла и условия продолжения цикла.

В подготовку цикла входят действия, связанные с заданием исходных значений для параметров цикла:

• начальные значения цикла;
• конечные значения цикла;
• шаг цикла.

В тело цикла входят:

• многократно повторяющиеся действия для вычисления искомых величин;
• подготовка следующего значения параметра цикла;
• подготовка других значений, необходимых для повторного выполнения действий в теле цикла.

В условии продолжения цикла определяется допустимость выполнения повторяющихся действий. Если параметр цикла равен или превысил конечное значение цикла, то выполнение цикла должно быть прекращено.

Пример

ЗАДАЧА. Разработать алгоритм вычисления суммы натуральных чисел от 1 до 100.

Этап 1. Математическое описание решения задачи.

Обозначим сумму натуральных чисел через S. Тогда формула вычисления суммы натуральных чисел от 1 до 100 может быть записана так:

где Xi – натуральное число X c номером i, который изменяется от 1 до n, n=100 – количество натуральных чисел.

Этап 2. Определение входных и выходных данных.

Входными данными являются натуральные числа: 1, 2, 3, 4, 5, …, 98, 99, 100.

Выходные данные – значение суммы членов последовательности натуральных чисел.

Параметр цикла – величина, определяющая количество повторений цикла. В нашем случае i – номер натурального числа.

Подготовка цикла заключается в задании начального и конечного значений параметра цикла.

• начальное значение параметра цикла равно 1,
• конечное значение параметра цикла равно n,
• шаг цикла равен 1.

Для корректного суммирования необходимо предварительно задать начальное значение суммы, равное 0.

Тело цикла. В теле цикла будет выполняться накопление значения суммы чисел, а также вычисляться следующее значение параметра цикла по формулам:

Условие продолжения цикла: цикл должен повторяться до тех пор, пока не будет добавлен последний член последовательности натуральных чисел, т.е. пока параметр цикла будет меньше или равен конечному значению параметра цикла.

Этап 3. Разработка алгоритма решения задачи.

Введем обозначения: S – сумма последовательности, i – значение натурального числа.

Начальное значение цикла i=1, конечное значение цикла i =100, шаг цикла 1.

Видео:Линейное уравнение с одной переменной. 6 класс.Скачать

Решение простых линейных уравнений

О чем эта статья:

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Видео:Метод Крамера за 3 минуты. Решение системы линейных уравнений - bezbotvyСкачать

Понятие уравнения

Уравнение — это математическое равенство, в котором неизвестна одна или несколько величин. Значение неизвестных нужно найти так, чтобы при их подстановке в пример получилось верное числовое равенство.

Например, возьмем выражение 2 + 4 = 6. При вычислении левой части получается верное числовое равенство, то есть 6 = 6.

Уравнением можно назвать выражение 2 + x = 6, с неизвестной переменной x, значение которой нужно найти. Результат должен быть таким, чтобы знак равенства был оправдан, и левая часть равнялась правой.

Корень уравнения — то самое число, которое при подстановке на место неизвестной уравнивает выражения справа и слева.

Решить уравнение значит найти все возможные корни или убедиться, что их нет.

Решить уравнение с двумя, тремя и более переменными — это два, три и более значения переменных, которые обращают данное выражение в верное числовое равенство.

Равносильные уравнения — это те, в которых совпадают множества решений. Другими словами, у них одни и те же корни.

Видео:Решение системы линейных уравнений графическим методом. 7 класс.Скачать

Какие бывают виды уравнений

Уравнения могут быть разными, самые часто встречающиеся — линейные и квадратные.

Особенность преобразований алгебраических уравнений в том, что в левой части должен остаться многочлен от неизвестных, а в правой — нуль.

Числовой коэффициент — число, которое стоит при неизвестной переменной.

Кроме линейных и квадратных есть и другие виды уравнений, с которыми мы познакомимся в следующий раз:

Онлайн-курсы по математике за 7 класс помогут закрепить новые знания на практике с талантливым преподавателем.

Видео:Линейное уравнение с двумя переменными. 7 класс.Скачать

Как решать простые уравнения

Чтобы научиться решать простые линейные уравнения, нужно запомнить формулу и два основных правила.

1. Правило переноса. При переносе из одной части в другую, член уравнения меняет свой знак на противоположный.

Для примера рассмотрим простейшее уравнение: x+3=5

Начнем с того, что в каждом уравнении есть левая и правая часть.

Перенесем 3 из левой части в правую и меняем знак на противоположный.

Можно проверить: 2 + 3 = 5. Все верно. Корень равен 2.

Решим еще один пример: 6x = 5x + 10.

Перенесем 5x из правой части в левую. Знак меняем на противоположный, то есть на минус.

Приведем подобные и завершим решение.

2. Правило деления. В любом уравнении можно разделить левую и правую часть на одно и то же число. Это может ускорить процесс решения. Главное — быть внимательным, чтобы не допустить глупых ошибок.

Применим правило при решении примера: 4x=8.

При неизвестной х стоит числовой коэффициент — 4. Их объединяет действие — умножение.

Чтобы решить уравнение, нужно сделать так, чтобы при неизвестной x стояла единица.

Разделим каждую часть на 4. Как это выглядит:

Теперь сократим дроби, которые у нас получились и завершим решение линейного уравнения:

Рассмотрим пример, когда неизвестная переменная стоит со знаком минус: −4x = 12

Разделим обе части на −4, чтобы коэффициент при неизвестной стал равен единице.

−4x = 12 | : (−4)
x = −3

Если знак минус стоит перед скобками, и по ходу вычислений его убрали — важно не забыть поменять знаки внутри скобок на противоположные. Этот простой факт позволит не допустить обидные ошибки, особенно в старших классах.

Напомним, что не у каждого линейного уравнения есть решение — иногда корней просто нет. Изредка среди корней может оказаться ноль — ничего страшного, это не значит, что ход решения оказался неправильным. Ноль — такое же число, как и остальные.

Способов решения линейных уравнений немного, нужно запомнить только один алгоритм, который будет эффективен для любой задачки.

Чтобы быстрее запомнить ход решения и формулу линейного уравнения, скачайте или распечатайте алгоритм — храните его в телефоне, учебнике или на рабочем столе.

Видео:Решение систем уравнений методом подстановкиСкачать

Примеры линейных уравнений

Теперь мы знаем, как решать линейные уравнения. Осталось попрактиковаться на задачках, чтобы чувствовать себя увереннее на контрольных. Давайте решать вместе!

Пример 1. Как правильно решить уравнение: 6х + 1 = 19.

Перенести 1 из левой части в правую со знаком минус.

Разделить обе части на множитель, стоящий перед переменной х, то есть на 6.

Пример 2. Как решить уравнение: 5(х − 3) + 2 = 3 (х − 4) + 2х − 1.

5х − 15 + 2 = 3х − 12 + 2х − 1

Сгруппировать в левой части члены с неизвестными, а в правой — свободные члены. Не забываем при переносе из одной части уравнения в другую поменять знаки на противоположные у переносимых членов.

5х − 3х − 2х = −12 − 1 + 15 − 2

Приведем подобные члены.

Ответ: х — любое число.

Пример 3. Решить: 4х = 1/8.

Разделим обе части уравнения на множитель стоящий перед переменной х, то есть на 4.

Пример 4. Решить: 4(х + 2) = 6 − 7х.

1. 4х + 8 = 6 − 7х
2. 4х + 7х = 6 − 8
3. 11х = −2
4. х = −2 : 11
5. х = −2/11

Ответ: −2/11 или −(0,18). О десятичных дробях можно почитать в другой нашей статье.

Пример 5. Решить:

1. 
2. 3(3х — 4) = 4 · 7х + 24
3. 9х — 12 = 28х + 24
4. 9х — 28х = 24 + 12
5. -19х = 36
6. х = 36 : (-19)
7. х = — 36/19

Пример 6. Как решить линейное уравнение: х + 7 = х + 4.

5х — 15 + 2 = 3х — 2 + 2х — 1

Сгруппировать в левой части неизвестные члены, в правой — свободные члены:

Приведем подобные члены.

Ответ: нет решений.

Пример 7. Решить: 2(х + 3) = 5 − 7х.

Видео:Алгебра 7 Линейное уравнение с одной переменнойСкачать

Линейный алгоритм. Понятие и особенности. Блок-схема

Каждый человек на протяжении своей жизни решает множество задач разной сложности. Но даже самые простые из задач выполняются последовательно, то есть за несколько шагов. Эту последовательность можно назвать алгоритмом. Последовательности бывают разные, но начинать их изучение лучше всего с линейных.

Прежде чем приступить к рассмотрению основной темы статьи, следует сделать краткое отступление и сказать несколько слов про алгоритмический язык.

Видео:Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

Алгоритмический язык

Представьте, что человеку, работающему за компьютером, поставлена некая вычислительная задача. В языке программирования решение этой задачи выполняется с помощью алгоритмизации. Решение предполагает: — разбиение на этапы; — разработку алгоритма; — составление программы решения на алгоритмическом языке; — ввод данных; — отладку программы (возможны ошибки — их надо исправить); — выполнение на ПК; — анализ результатов.

Алгоритмический язык является средством описания алгоритмов, а уже алгоритм, в свою очередь, представляет собой чёткое описание определённой последовательности действий, направленных на решение необходимой задачи.

Видео:0.Блок схема. 8 классСкачать

Свойства алгоритма

Их несколько: — конечность. Любой алгоритм должен быть завершённым, а окончание наступает после выполнения определённого числа шагов; — однозначность, понятность. Не допускается разных толкований, неопределённости и двусмысленности — всё должно быть чётко и ясно, а также понятно исполнителю — и правила выполнения действий линейного алгоритма, и сами действия; — результативность. Итог работы — результат, полученный за конечное число шагов; — универсальность, массовость. Качественный алгоритм способен решать не одну задачу, а целый класс задач, имеющих схожую постановку/структуру.

Видео:ЛИНЕЙНОЕ УРАНЕНИЕ С ДВУМЯ ПЕРЕМЕННЫМИ — Как решать линейное уравнение // Алгебра 7 классСкачать

Линейная структура

Любой алгоритм составляется из ряда базовых структур. Простейшей базовой структурой является следование — структура с линейными характеристиками. Из этого можно сформулировать определение.

Линейный алгоритм — это алгоритм, образуемый командами, которые выполняются однократно и именно в той последовательности, в которой записаны. Линейная структура, по сути, проста. Записать её можно как в текстовой, так и в графической форме.

Представим, что у нас стоит задача пропылесосить ковёр в комнате. В текстовой форме алгоритм будет следующим: — принести пылесос к месту уборки; — включить; — пропылесосить; — выключить; — унести пылесос.

И каждый раз, когда нам надо будет пылесосить, мы будем выполнять один и тот же алгоритм.

Теперь поговорим про графическую форму представления.

Блок-схема

Для изображения алгоритма графически используют блок-схемы. Они представляют собой геометрические фигуры (блоки), соединённые стрелками. Стрелки показывают связь между этапами и последовательность их выполнения. Каждый блок сопровождается надписью.

Рассмотрим фигуры, которые используются при визуализации типичной линейной последовательности.

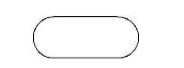
Блок ввода-вывода данных (отображает список вводимых и выводимых переменных):

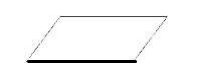
Арифметический блок (отображает арифметическую операцию/группу операций):

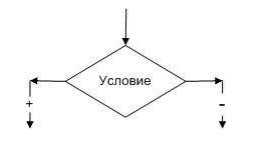
Условный блок (позволяет описать условие). Алгоритмы с таким блоком используются при графической визуализации алгоритмов с ветвлением:

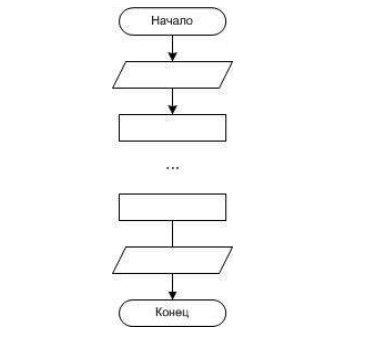
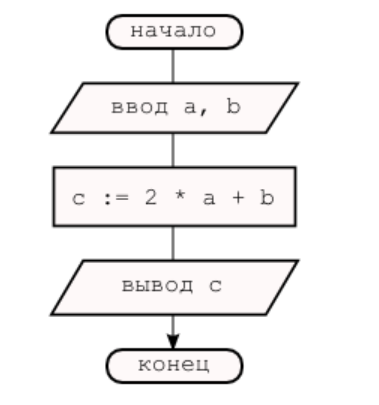
Условного блока нет в классическом линейном алгоритме, так как в нём, как уже было сказано ранее, все операции выполняются последовательно, то есть одна за другой. В линейном алгоритме размещение блоков выглядит следующим образом:

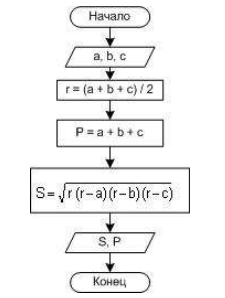
А вот, как решается задача по нахождению площади треугольника по формуле Герона. Здесь a, b, c – это длины сторон, S – площадь треугольника, P – периметр.

Следует обратить внимание, что запись «=» — это не математическое равенство, а операция присваивания. В результате этой операции переменная, стоящая слева от оператора, получает значение, которое указано справа. Значение не обязательно должно быть сразу определено (a = 3) — оно может вычисляться посредством выражения (a = b + z), где b = 1, a z = 2.

Видео:Алгоритм решения задач с помощью систем уравнений. Практическая часть. 9 класс.Скачать

Примеры линейных алгоритмов

Если рассмотреть примеры решения на языке Pascal (именно этот язык до сих пор используется для изучения основ алгоритмизации и программирования), то можно увидеть следующую картину:

И, соответственно, блок-схема программы линейной структуры будет выглядеть следующим образом:

Видео:Математика без Ху!ни. Метод Гаусса.Скачать

Как составить программу линейной структуры?

Порядок следующий: — определите, что именно относится к исходным данными, а также каков типы/класс этих данных, выберите имена переменных; — определите, каков тип данных будет у искомого результата, выберите название переменных (переменной); — определите, какие математические формулы связывают результат и исходные данные; — если требуется наличие промежуточных данных, определите класс/типы этих данных и выберите имена; — опишите все используемые переменные; — запишите окончательный алгоритм. Он должен включать в себя ввод данных, вычисления, вывод результатов.

На этом всё, в следующий раз рассмотрим на примерах программу разветвлённой структуры. Если же вас интересует тема алгоритмизации в контексте разработки программного обеспечения, ждём вас на профессиональном курсе OTUS!

🔍 Видео

Решение системы уравнений методом ГауссаСкачать

Решение системы линейных уравнений с двумя переменными способом подстановки. 6 класс.Скачать

МЕТОД ПОДСТАНОВКИ 😉 СИСТЕМЫ УРАВНЕНИЙ ЧАСТЬ I#математика #егэ #огэ #shorts #профильныйегэСкачать

ГРАФИК ЛИНЕЙНОГО УРАВНЕНИЯ С ДВУМЯ ПЕРЕМЕННЫМИ 7 КЛАСС видеоурокСкачать

Как решать уравнения с модулем или Математический торт с кремом (часть 1) | МатематикаСкачать

7 класс, 4 урок, Линейное уравнение с одной переменнойСкачать

Линейное уравнение с одной переменнойСкачать