Если законы функционирования модели нелинейны, а моделируемые процесс или система обладают одной степенью свободы (т.е. имеют одну независимую переменную), то такая модель, как правило, описывается одним нелинейным уравнением.
Необходимость отыскания корней нелинейных уравнений встречается в расчетах систем автоматического управления и регулирования, собственных колебаний машин и конструкций, в задачах кинематического анализа и синтеза, плоских и пространственных механизмов и других задачах.
Дано нелинейное уравнение:
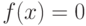 | ( 4.1) |
Необходимо решить это уравнение, т. е. найти его корень 
Если функция имеет вид многочлена степени m,
где ai — коэффициенты многочлена, 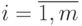
Если функция f(x) включает в себя тригонометрические или экспоненциальные функции от некоторого аргумента x , то уравнение (4.1) называется трансцендентным уравнением .
Такие уравнения обычно имеют бесконечное множество решений.
Как известно, не всякое уравнение может быть решено точно. В первую очередь это относится к большинству трансцендентных уравнений .
Доказано также, что нельзя построить формулу, по которой можно было бы решать произвольные алгебраические уравнения степени, выше четвертой.
Однако точное решение уравнения не всегда является необходимым. Задачу отыскания корней уравнения можно считать практически решенной, если мы сумеем найти корни уравнения с заданной степенью точности . Для этого используются приближенные (численные) методы решения.
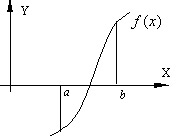
Большинство употребляющихся приближенных методов решения уравнений являются, по существу, способами уточнения корней. Для их применения необходимо знание интервала изоляции [a,b] , в котором лежит уточняемый корень уравнения (рис. 4.3).
Процесс определения интервала изоляции [a,b] , содержащего только один из корней уравнения, называется отделением этого корня.
Процесс отделения корней проводят исходя из физического смысла прикладной задачи, графически, с помощью таблиц значений функции f(x) или при помощи специальной программы отделения корней. Процедура отделения корней основана на известном свойстве непрерывных функций: если функция непрерывна на замкнутом интервале [a,b] и на его концах имеет различные знаки, т.е. f(a)f(b) , то между точками a и b имеется хотя бы один корень уравнения (1). Если при этом знак функции f'(x) на отрезке [a,b] не меняется, то корень является единственным на этом отрезке.
Процесс определения корней алгебраических и трансцендентных уравнений состоит из 2 этапов:
- отделение корней, — т.е. определение интервалов изоляции [a,b] , внутри которого лежит каждый корень уравнения;
- уточнение корней, — т.е. сужение интервала [a,b] до величины равной заданной степени точности
.
Для алгебраических и трансцендентных уравнений пригодны одни и те же методы уточнения приближенных значений действительных корней:
Видео:13 Шаговый метод Ручной счет Численные методы решения нелинейного уравненияСкачать

Нелинейные уравнения и системы уравнений. Методы их решения.
Видео:Метод простых итераций пример решения нелинейных уравненийСкачать

Нелинейные уравнения и системы уравнений. Методы их решения.
Одной из важных задач прикладной математики является задача решения нелинейных уравнений, встречающихся в разных областях научных исследований.
Под нелинейными уравнениями ( nonlinear equations ) понимаются алгебраические и трансцендентные уравнения с одним неизвестным в следующем виде:

где 

Под системой нелинейных уравнений понимается система алгебраических и трансцендентных уравнений в следующем виде:
где < 


Алгебраическое уравнение — это уравнение содержащие только алгебраические функции, которое можно представить многочленом n ‐ ой степени с действительными коэффициентами (целые, рациональные, иррациональные) в следующем виде:

Трансцендентное уравнение – это уравнение содержащие в своем составе функции, которые являются не алгебраическими. Простейшими примерами таких функций служат показательная функция, тригонометрическая функция, логарифмическая функция и т.д.
Решением нелинейного уравнения (или системы нелинейных уравнений) называют совокупность (группа) чисел 


Для решения нелинейных уравнений (или систем нелинейных уравнений) существует несколько методов решения: графические, аналитические и численные методы.
Графические методы наименее точны, но позволяют в сложных уравнениях определить наиболее приближенные значения, с которых в дальнейшем можно начинать находить более точные решения уравнений.
Аналитические методы (или прямые методы) позволяют определить точные значения решения уравнений. Данный метод позволяет записать корни в виде некоторого соотношения (формул). Подобные методы развиты для решения простейших тригонометрических, логарифмических, показательных, а также алгебраических уравнений. Однако подавляющее большинство нелинейных уравнений, встречающихся на практике, не удается решить прямыми методами. В таких случаях обращаются к численным методам, позволяющим получить приближенное значение корня с любой заданной точностью 
Численные методы решения нелинейных уравнений – это итерационный процесс расчета, который состоит в последовательном уточнении начального приближения значений корней уравнения (системы уравнений). При численном подходе задача о решении нелинейных уравнений разбивается на два этапа:
— локализация (отделение) корней
› Под локализацией корней понимается процесс отыскания приближенного значения корня или нахождение таких отрезков, в пределах которых содержится единственное решение
› Под уточнением корней понимается процесс вычисления приближенных значений корней с заданной точностью по любому численному методу решения нелинейных уравнений.
Недостатком почти всех итерационных методов нахождения корней является то, что они при однократном применении позволяют найти лишь один корень функции, к тому же, мы не знаем какой именно. В случае повторения итерационного процесса при изменении стартовых точек отсутствуют гарантии, что найдется новый корень уравнения, так как итерационный процесс может сойтись к найденному корню.
Для поиска других корней используется метод удаления корней. Данный метод основан на принципе создания новой функции 

Так, например, если 








Следует обратить внимание, что когда производим деление на тот или иной корень 



Локализация корней.
› Локализация корней аналитическим способом
Для отделения корней уравнения 







› Локализация корней табличным способом
Допустим, что все интересующие нас корни уравнения 




Надежность рассмотренного подхода к отделению корней уравнений зависит как от характера функции 








Рис. 1. Варианты поведения функции на интервале локализации корня
Поскольку данный способ предполагает выполнение лишь элементарных арифметических и логических операций, количество которых может быть велико при малых значениях h , для его реализации целесообразно использовать вычислительные возможности компьютера.
Отделяя, таким образом, корни, мы, по сути, получаем их приближенные значения с точностью до выбранного шага. Так, например, если в качестве приближенного значения корня взять середину отрезка локализации, то абсолютная погрешность этого значения не будет превосходить половины шага поиска ( h /2). Уменьшая шаг в окрестности каждого корня, можно, в принципе, повысить точность отделения корней до любого наперед заданного значения. Однако такой способ требует большого объема вычислений. Поэтому при проведении численных экспериментов с варьированием параметров задачи, когда приходится многократно осуществлять поиск корней, подобный метод не годится для уточнения корней и используется только для отделения (локализации) корней, т.е. определения начальных приближений к ним. Уточнение корней проводится с помощью других, более экономичных методов.
Уточнение корней.
На данном этапе задача состоит в получении приближенного значения корня, принадлежащего отрезку 


Существует большое количество численных методов решения нелинейных уравнений для уточнения корней, которые условно можно разделить:
› Методы решение уравнений с одним неизвестным. Основными представителями являются:
— метод половинного деления;
— метод простой итерации;
— метод Ньютона для уравнения с одним неизвестным;
🌟 Видео
10 Численные методы решения нелинейных уравненийСкачать

4 Шаговый метод Calc Excel Численные методы решения нелинейного уравненияСкачать

Численные методы решения нелинейного уравнени Теория Шаговый Метод половинного деления Метод НьютонаСкачать

Способы решения систем нелинейных уравнений. 9 класс.Скачать

Метод Ньютона (метод касательных) Пример РешенияСкачать

Шаговый метод Ручной счет Численные методы решения нелинейного уравненияСкачать

Численное решение уравнений, урок 3/5. Метод хордСкачать

1 3 Решение нелинейных уравнений методом простых итерацийСкачать

1 Шаговый метод Блок-схема Численные методы решения нелинейного уравненияСкачать

3 Шаговый метод Mathcad Численные методы решения нелинейного уравненияСкачать

Решение нелинейного уравнения методом простых итераций (программа)Скачать

Шаговый метод Excel Эксель Численные методы решения нелинейного уравнения Шаговый метод в экселеСкачать

После этого видео, ТЫ РЕШИШЬ ЛЮБУЮ Систему Нелинейных УравненийСкачать

4.2 Решение систем нелинейных уравнений. МетодыСкачать

2 Шаговый метод C++ Численные методы решения нелинейного уравненияСкачать

3 Теория: Численные методы решения нелинейного уравнения Шаговый, половинного деления, НьютонаСкачать

Способы решения систем нелинейных уравнений. Практическая часть. 9 класс.Скачать

Метод половинного деления решение нелинейного уравненияСкачать


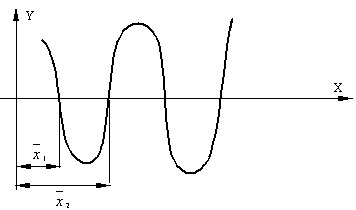
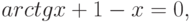

 .
.

