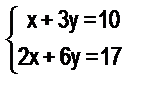Сформулируйте условия при которых число 5 является корнем уравнения f x g x (7 видео)

Равносильные уравнения. Теоремы о равносильности уравнений

Определение. Два уравнения f₁(х) = g₁(х) и f₂(х) = g₂(х) называются равносильными, если множества их корней совпадают.

Например, уравнения х 2 — 9 = 0 и (2 х + 6)( х — 3) = 0 равносильны, так как оба имеют своими корнями числа 3 и -3. Равносильны и уравнения (3х + 1)-2 = х 2 — + 1 и х 2 + 1 = 0, так как оба не имеют корней, т.е. множества их корней совпадают.

Определение. Замена уравнения равносильным ему уравнением называется равносильным преобразованием.

Выясним теперь, какие преобразования позволяют получать равносильные уравнения.

Теорема 1.Пусть уравнение f(х) и g(х)задано на множестве и h(x) — выражение, определенное на том же множестве. Тогда уравнения f(х) = g(х) (1)и f(х) + h(x) = g(х) + h(x) (2) равносильны.

Доказательство. Обозначим через Т₁ — множество решений уравнения (1), а через Т₂ — множество решений уравнения (2). Тогда уравнения (1) и (2) будут равносильны, если Т₁ = Т₂. Чтобы убедиться в этом, необходимо показать, что любой корень из Т₁ является корнем уравнения (2) и, наоборот, любой корень из Т₂ является корнем уравнения (1).

Пусть число а — корень уравнения (1). Тогда a ? Т₁, и при подстановке в уравнение (1) обращает его в истинное числовое равенство f(a) = g(a), а выражение h(х) обращает в числовое выражение h(a), имеющее смысл на множестве X. Прибавим к обеим частям истинного равенства f(a) = g(a) числовое выражение h(a). Получим, согласно свойствам истинных числовых равенств, истинное числовое равенство f(a) + h(a) = g(a) + h(a), которое свидетельствует о том, что число а является корнем уравнения (2).

Итак, доказано, что каждый корень уравнения (1) является корнем и уравнения (2), т.е. Т₁ с T₂.

Пусть теперь а — корень уравнения (2). Тогда а ? T₂ и при подстановке в уравнение (2) обращает его в истинное числовое равенство f(a) + h(a) = g(a) + h(a). Прибавим к обеим частям этого равенства числовое выражение —h(a), Получим истинное числовое равенство f(х) = g(х), которое свидетельствует о том, что число а — корень уравнения (1).

Итак, доказано, что каждый корень уравнения (2) является и корнем уравнения (1), т.е. T₂ с Т₁.

Так как Т₁ с Т₂ и Т₂ с Т₁, то по определению равных множеств Т₁ = Т₂, а значит, уравнения (1) и (2) равносильны.

Данную теорему можно сформулировать иначе: если к обеим частям уравнения с областью определения X прибавить одно и то же выражение с переменной, определенное на том же множестве, то получим новое уравнение, равносильное данному.

Из этой теоремы вытекают следствия, которые используются при решении уравнений:

1.Если к обеим частям уравнения прибавить одно и то лее число, то получим уравнение, равносильное данному.

2. Если какое-либо слагаемое (числовое выражение или выражение с переменной) перенести из одной части уравнения в другую, поменяв знак слагаемого на противоположный, то получим уравнение, равносильное данному.

Теорема 2. Пусть уравнение f(х) = g(х) задано на множестве X и h(х) — выражение, которое определено на том же множестве и не обращается в нуль ни при каких значениях х из множества X. Тогда уравнения f(х) = g(х) и f(х) · h(x) = g(х) · h(x) равносильны.

Доказательство этой теоремы аналогично доказательству теоремы 1.

Теорему 2 можно сформулировать иначе: если обе части уравнения с областью определения X умножить на одно и то же выражение, которое определено на том же множестве и не обращается на нем в нуль, то получим новое уравнение, равносильное данному.

Из этой теоремы вытекает следствие: если обе части уравнения умножить (или разделить) на одно и то же число, отличное от нуля, то получим уравнение, равносильное данному.

Решение уравнений с одной переменной

Решим уравнение 1- x/3 = x/6, x ? R и обоснуем все преобразования, которые мы будем выполнять в процессе решения.

Преобразования	Обоснование преобразования
1. Приведем выражения, стоящие в левой и правой частях уравнения, к общему знаменателю: (6-2х)/ 6 = х/6	Выполнили тождественное преобразование выражения в левой части уравнения.
2. Отбросим общий знаменатель: 6-2х = х	Умножили на 6 обе части уравнения (теорема 2), получили уравнение, равносильное данному.
3. Выражение -2х переносим в правую часть уравнения с противоположным знаком: 6 = х+2х.	Воспользовались следствием из теоремы 1, получили уравнение, равносильное предыдущему и, значит, данному.
4. Приводим подобные члены в правой части уравнения: 6 = 3х.	Выполнили тождественное преобразование выражения.
5. Разделим обе части уравнения на 3: х = 2.	Воспользовались следствием из теоремы 2, получили уравнение, равносильное предыдущему, а значит, и данному

Так как все преобразования, которые мы выполняли, решая данное уравнение, были равносильными, то можно утверждать, что 2 — корень этого уравнения.

Если же в процессе решения уравнения не выполняются условия теорем 1 и 2, то может произойти потеря корней или могут появиться посторонние корни. Поэтому важно, осуществляя преобразования уравнения с целью получения более простого, следить за тем, чтобы они приводили к уравнению, равносильному данному.

Рассмотрим, например, уравнение х(х — 1) = 2х, х ? R. Разделим обе части на х, получим уравнение х — 1 = 2, откуда х = 3, т. е. данное уравнение имеет единственный корень — число 3. Но верно ли это? Нетрудно видеть, что если в данное уравнение вместо переменной х подставить 0, оно обратится в истинное числовое равенство 0·(0 — 1) = 2·0. А это означает, что 0 — корень данного уравнения, который мы потеряли, выполняя преобразования. Проанализируем их. Первое, что мы сделали, — это разделили обе части уравнения на х, т.е. умножили на выражение1/x , но при х = О оно не имеет смысла. Следовательно, мы не выполнили условие теоремы 2, что и привело к потере корня.

Чтобы убедиться в том, что множество корней данного уравнения состоит из двух чисел 0 и 3, приведем другое его решение. Перенесем выражение 2х из правой части в левую: х(х — 1) — 2х = 0. Вынесем в левой части уравнения за скобки х и приведем подобные члены: х(х — 3) = 0. Произведение двух множителей равно нулю в том и только в том случае, когда хотя бы один из них равен нулю, поэтому x= 0 или х — 3 = 0. Отсюда получаем, что корни данного уравнения — 0 и 3.

В начальном курсе математики теоретической основой решения уравнений является взаимосвязь между компонентами и результатами действий. Например, решение уравнения (х·9):24 = 3 обосновывается следующим образом. Так как неизвестное находится в делимом, то, чтобы найти делимое, надо делитель умножить на частное: х ·9 = 24·3, или х·9 = 72.

Чтобы найти неизвестный множитель, надо произведение разделить на известный множитель: х = 72:9, или х = 8, следовательно, корнем данного уравнения является число 8.

Упражнения

1. Установите, какие из следующих записей являются уравнениями с одной переменной:

а) (х -3)·5 = 12х; г) 3 + (12-7)· 5 = 16;

в) (х-3)·17 + 12; е) х 2 — 2х + 5 = 0.

2.Уравнение 2 х 4 + 4 х 2 -6 = 0 задано на множестве натуральных чисел. Объясните, почему число 1 является корнем этого уравнения, а 2 и -1 не являются его корнями.

3.В уравнении (х + . )(2 х + 5) — (х — 3)(2 х + 1) = 20 одно число стерто и заменено точками. Найдите стертое число, если известно, что корнем этого уравнения является число 2.

4.Сформулируйте условия, при которых:

а) число 5 является корнем уравнения f(х) = g(х);

б) число 7 не является корнем уравнения f(х) = g(х).

5. Установите, какие из следующих пар уравнений равносильны на множестве действительных чисел:

а) 3 + 7 х = -4 и 2(3 + 7л х) = -8;

6)3 + 7 х = -4 и 6 + 7 х = -1;

в)3 + 7 х = -4 и л х + 2 = 0.

6. Сформулируйте свойства отношения равносильности уравнений. Какие из них используются в процессе решения уравнения?

7. Решите уравнения (все они заданы на множестве действительных чисел) и обоснуйте все преобразования, выполняемые в процессе их упрощения:

8. Учащийся решил уравнение 5 х + 15 = 3 х + 9 следующим образом: вынес за скобки в левой части число 5, а в правой число 3, получил уравнение 5(х + 3) = 3(х + 3), а затем разделил обе части на выражение х + 3. Получил равенство 5 = 3 и сделал вывод – данное уравнение корней не имеет. Прав ли учащийся?

9. Решите уравнение 2/(2-x) – ½ = 4/((2-x)x); х ? R. Является ли число 2 корнем этого уравнения?

10. Решите уравнения, используя взаимосвязь между компонентами и результатами действий:

а) (х + 70)·4 = 328; в) (85 х + 765): 170 = 98;

б) 560: (х + 9) — 56; г) (х — 13581):709 = 306.

11. Решите задачи арифметическим и алгебраическим способами:

а) На первой полке на 16 книг больше, чем на второй. Если с каждой полки снять по 3 книги, то на первой полке книг будет в полтора раза больше, чем на второй. Сколько книг на каждой полке?

б) Весь путь от турбазы до станции, равный 26 км, велосипедист проехал за 1 ч 10 мин. Первые 40 мин этого времени он ехал с одной скоростью, а остальное время — со скоростью на 3 км/ч меньше. Найдите скорость велосипедиста на первом участке пути.

Видео:Математика 5 класс. Уравнение. Корень уравненияСкачать

ПРАКТИЧЕСКАЯ РАБОТА. УРАВНЕНИЯ И НЕРАВЕНСТВА С ОДНОЙ ПЕРЕМЕННОЙ.

Цель.Углубить знания о числовых неравенствах и равенствах. Раскрыть трактовку понятий равенства и неравенства в начальном курсе математики.

Теоретическая часть

Вопросы к изучению

1. Уравнения с одной переменной.

2. Теоремы о равносильности уравнений с одной переменной.

3. Неравенства с одной переменной.

4. Теоремы о равносильности неравенств с одной переменной.

Основные понятия темы

Ø уравнение с одной переменной;

Ø корень уравнения;

Ø что значит решить уравнение;

Ø равносильные уравнения;

Ø неравенство с одной переменной;

Ø решение неравенства;

Ø что значит решить неравенство;

Ø равносильные неравенства.

Замечания, выводы

Ø рассмотрены теоремы о равносильности уравнений и неравенств, являющиеся основой их решения.

Ø Знание определений всех названных выше понятий и теорем о равносильности уравнений и неравенств — необходимое условие методически грамотного изучения с младшими школьниками алгебраического материала.

Практическая часть

1. Установите, какие из следующих записей являются уравнениями с одной переменной:

а) (х-3) × 5= 12х; г) 3+(12-7) × 5 = 16;

б) (х-3) × 5= 12; д) (х-3) × у =12х;

в) (х-3) × 17+ 12; е) х 2 — 2х + 5 = 0.

2. Уравнение 2х 4 + 4х 2 -6=0 задано на множестве натуральных чисел. Объясните, почему число 1 является корнем этого уравнения, а 2 и -1 не являются его корнями.

3. В уравнении (х + . )(2х + 5) — (х — 3)(2х + 1) = 20 одно число стерто и заменено точками. Найдите стертое число, если известно, что корнем этого уравнения является число 2.

4. Сформулируйте условия, при которых: а) число 5 является корнем уравнения f(х) = q(х); б) число 7 не является корнем уравнения f(х) = q(х).

5. Установите, какие из следующих пар уравнений равносильны на множестве действительных чисел:

а) 3+7х= — 4 и 2(3+7х)= — 8; б) 3+7х = — 4 и 6+7х = — 1; в) 3+7х = — 4 и х + 2=0.

а) ; б) х — ; в) (2 – х) 2 – х ( х – 1,5) = 4.

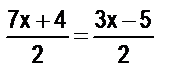
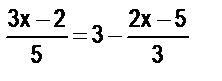
8. Учащийся решил уравнение 5х + 15 = 3х + 9 следующим образом: вынес за скобки в левой части число 5, а в правой число 3, получил уравнение 5(х + 3) = 3(х + 3), а затем разделил обе части на выражение х + 3. Получил равенство 5 = 3 и сделал вывод – данное уравнение корней не имеет. Прав ли учащийся?

9. Решите уравнение 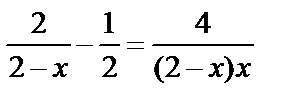; х ÎR. Является ли число 2 корнем этого уравнения?

10. Решите уравнения, используя взаимосвязь между компонентами и результатами действий:

а) (х + 70) • 4 = 328; в) (85х + 765): 170 = 98;

б) 560 : (х + 9) = 56; г) (х — 13581): 709 = 306.

11. Решите задачи арифметическим и алгебраическим способами:

12. Установите, какие из следующих записей являются неравенствами с одной переменной:

а) — 12 — 7х 4; д) 17-12 × 8;

в) 17× (13+8) 2 + 3х – 4 > 0.

13. Является ли число 3 решением неравенства 6 (2х + 7) 3; б) 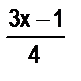> 0 и 3х – 1 >0; в) 6 — 5х > — 4 и х 4; б) х 3 — (1-2х) является любое действительное число.

18. Докажите, что не существует действительного числа, которое являлось бы решением неравенства 3(2 — х)-2 > 5- 3х.

19. Одна сторона треугольника равна 5 см, а другая 8 см. Какой может быть длина третьей стороны, если периметр треугольника: а) меньше 22 см; б) больше 17 см?

1. Решите задачу различными алгебраическими способами: «От деревни до совхоза 20 км, а от совхоза до станции 40 км. Из совхоза по направлению к станции выехал велосипедист со скоростью 12 км/час. Одновременно на станцию через совхоз по той же дороге отправился мотоциклист. С какой скоростью должен ехать мотоциклист, чтобы догнать велосипедиста до его приезда на станцию?».

2. Решите задачу алгебраическим и арифметическим методом: «В двух пачках всего 30 тетрадей, Если бы из первой пачки переложили во вторую 2 тетради, то в первой пачке стало бы вдвое больше тетрадей, чем в первой. Сколько тетрадей было в каждой пачке?».

3. Решите задачу алгебраически и проверьте, решив арифметически: «Из пункта А выехал велосипедист. Одновременно вслед за ним из пункта В, отстоящего от А на 20 км, выехал мотоциклист. Велосипедист ехал со скоростью 12 км/час, а мотоциклист со скорость. 16 км/час. на каком расстоянии от пункта А догонит мотоциклист велосипедиста?».

4. Решите задачу арифметическим методом и проверьте, решив ее алгебраическим: «В двух кусках одинаковое количество тканей. После того как от одного куска отрезали 18 м, а от другого 25 м, в первом куске осталось вдвое больше ткани, чем во втором. Сколько метров ткани было в каждом куске?».

5. Решите задачу алгебраическим методом. Что в условии задачи явилось обоснованием к составлению уравнения? Бригада рабочих должна была за определенный срок изготовить 400 деталей. В течение 5 дней бригада перевыполнила дневную норму на 20 %, а в последующие дни изготовляла ежедневно по 15 деталей сверх плана и уже за два дня до срока изготовила 405 деталей. Сколько деталей должна была изготовлять ежедневно бригада по плану?

6. Решите задачу. Какой метод решения задачи выбрали? Как выполнили проверку решения задачи? Группа туристов отправилась на экскурсию из города А в город В на пароходе, а возвратилась обратно по железной дороге. Расстояние от А до В по воде 96 км, а по железной дороге 72 км. Поезда по железной дороге продолжалась на 2 час. 40 мин. меньше, чем на пароходе. Средняя скорость парохода на 30 км/час меньше скорость поезда. Какова скорость движения парохода и поезда?

7. Составьте текстовые задачи по математической модели.

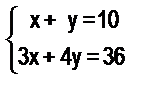
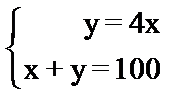
а) ; b) .

8. Составьте текстовые задачи, математической моделью которых являются неравенства: а) х + 5 £ 10; б) х + 5 ³ 5. Составленные задачи решите арифметически, алгебраически и графически. Сколько решений имеют составленные задачи?

9. Составьте текстовые задачи, моделью которых являются системы уравнений:

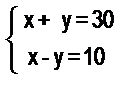
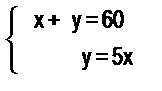
а) ; b) ; c)

Составленные задачи решите арифметически, алгебраически и графически. Какие величины рассматриваются в задачах?

Дата добавления: 2021-01-26 ; просмотров: 375 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Видео:Составьте квадратное уравнение, корнями которого являются числаСкачать

Алгебра 11кл — Конспект

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Рабочие листы и материалы для учителей и воспитателей

Более 2 500 дидактических материалов для школьного и домашнего обучения

УМК Алгебра и начала анализа 10-11 кл. : А.Г Мордкович

Уровень обучения базовый

Тема: «Равносильность уравнений»

Тип уроков: комбинированные уроки изучения нового материала, обобщения и систематизации знаний.

— обобщить и систематизировать знания учащихся по наиболее важным вопросам, связанным с преобразованиями и решением уравнений с одной переменной.

— развитие мышления учащихся; развитие познавательного интереса и умений учебно-познавательной деятельности.

воспитание организованности, самоконтроля и взаимоконтроля.

· изучение новых видов числовых выражений и формул;

· совершенствование практических навыков и вычислительной культуры, расширение и совершенствование алгебраического аппарата, сформированного в основной школе, и его применение к решению математических и нематематических задач;

· расширение и систематизация общих сведений о функциях, пополнение класса изучаемых функций, иллюстрация широты применения функций для описания и изучения реальных зависимостей;

· знакомство с основными идеями и методами математического анализа.

решать рациональные, показательные и логарифмические уравнения и, простейшие иррациональные и тригонометрические уравнения и их системы;

— составлять уравнения и по условию задачи;

— использовать для приближенного решения уравнений и графический метод;

— изображать на координатной плоскости множества решений простейших уравнений и их систем;

Организационные формы общения: индивидуальная, групповая.

Оборудование: модуль «Решение иррациональных уравнений».

I Организационный этап — 2 мин.

II Актуализация опорных знаний — 4 мин.

III Цели урока — 2 мин.

IV Изучение теоретического материала и способов деятельности — 20 мин.

V Закрепление учебного материала — 12 мин.

V Закрепление учебного материала — 25 мин.

VI Самостоятельная работа — 10 мин.

VII Домашнее задание — 3 мин.

VIII Выводы по уроку — 2 мин.

Проверка готовности обучающихся к уроку.

Краткое обсуждение с учащимися тех теоретических знаний, которыми они обладают и пользуются при решении уравнений.

Допустим, нам необходимо решить уравнение

Преобразуем данное уравнение, выстраивая цепочку уравнений и стараясь получить уравнение вида а х = b , т.е. линейное уравнение

6х — 15 = 2х + 5, 6х — 2х = 5 + 15, 4х = 20.

Откуда получаем, что 5 — корень уравнения. Причём, как последнего уравнения, так и любого из уравнений данной цепочки, так как они являются равносильными уравнениями. По сути, решением уравнения и является выстраивание подобных цепочек уравнений.

Однако при преобразовании уравнений (и неравенств в том числе) далеко не всегда легко получить им равносильные уравнения. И как быть тогда?

Изучением этих крайне важных вопросов нам и предстоит заняться.

Мы вернёмся к целому ряду понятий, связанных с решением уравнений, с которыми вы неплохо знакомы, и посмотрим на них как бы несколько иначе, глубже, обобщим и дополним рядом важных и принципиальных положений.

1) Определение. Два уравнения с одной переменной f (х) = g (х) и h (х) = р(х) называют равносильными, если они имеют одинаковые корни или если оба уравнения не имеют корней.

Например, уравнения — 4 = 0 и (х + 2)(2 Х — 4) = 0 равносильны; равносильны и уравнения х 2 + 1 = 0 и = — 2 — они не имеют корней.

2) Определение. Если каждый корень уравнения f (х) = g (х) (1) является в то же время корнем уравнения h (х) = р(х) (2), то уравнение (2) называется следствием уравнения (1).

Например, уравнение х — 2 = 3 имеет корень 5, уравнение — 25 = 0 имеет корни ± 5. Так как корень уравнения х — 2 = 3 является корнем уравнения х 2 — 25 = 0, то уравнение х 2 — 25 = 0 является следствием,, уравнения х — 2 = 3.

Следовательно, два уравнения называют равносильными тогда и только тогда, когда каждое из них является следствием другого.

3) Если в ходе преобразований, при переходе от одного из уравнений к уравнению-следствию, мы неуверенны в равносильности выполняемого перехода, то у последнего уравнения могут появиться посторонние корни в отношении исходного уравнения. Поэтому все полученные корни уравнения- следствия необходимо проверить, подставляя их в исходное уравнение. Тем самым, проверка найденных корней уравнения является не проверкой верности выполненных технических преобразований, а неотъемлемой частью, этапом решения уравнения.

4) Итак, мы выяснили, что в процессе решения уравнений (а ещё более при решении неравенств) на каждом этапе преобразований крайне важно знать, равносильный ли переход мы совершаем. Сформулируем и обсудим ряд важных для нас положений.

Теорема 1. Если какой-либо член уравнения перенести из одной части уравнения в другую с противоположным знаком, то получится уравнение, равносильное данному уравнению.

Теорема 2. Если обе части уравнения возвести в одну и ту же нечётную степень, то получится уравнение, равносильное данному уравнению.

Теорема 3 . Показательное уравнение (где > 1, 1 ) равносильно уравнению f (х) = g (х).

Определение . Областью определения уравнения f (х) = g (х) или ОДЗ переменной уравнения называется множество тех значений х, при которых одновременно имеют смысл обе части уравнения f (х) = g (х).

Теорема 4 . Если обе части уравнения f (х) = g (х) умножить на одно и то же выражение h (х), которое имеет смысл всюду в области определения (ОДЗ) уравнения f (х) = g (х) и при этом нигде в этой области h (х) 0 , то уравнения f (х) = g (х) и h (х)∙ f (х) = h (х) g (х) равносильны.

То есть, мы можем обе части уравнения умножать или делить на одно и то же отличное от нуля число, не нарушая при этом равносильности уравнений.

Теорема 5. Если обе части уравнения f (х) = g (х) неотрицательны на ОДЗ уравнения, то после возведения обеих его частей в одну и ту же степень n получится уравнение g n ( x ), равносильное исходному уравнению.

Теорема 6. Если f (х)>0, = g (х)>0 , то уравнение log_α 2 f ( x ) = log _α g ( x ) , где а>0, , равносильно уравнению f (х) = g (х).

5) Рассмотрим применение теоретических положений на практике. Пусть нам дано уравнение х — 1 = 3, корень которого равен 4.

а) Умножив обе части уравнения на выражение х — 2, получим уравнение (х — 1 )(х — 2) = 3(х — 2). Решим полученное уравнение

То есть, уравнение-следствие имеет два корня 2 и 4, причём, 2-посторонний корень для исходного уравнения. Каким образом у исходного уравнения появился посторонний корень? — Если бы мы вначале преобразовали исходное уравнение к виду х — 4 = 0. За тем домножили обе части уравнения на х — 2. То получили бы уравнение (х — 4)(х — 2) = 0, которое равносильно совокупности уравнении . Тогда понятно, что уравнение х — 2 = 0, по отношению к исходному уравнению х — 4 = 0, является посторонним уравнением, отсюда и появление постороннего корня. Фактически мы умножили обе части исходного уравнения на выражение х — 2, допуская при этом его равенство нулю, что невозможно по теореме 4.

б) Возведём в квадрат обе части уравнения х — 1 = 3. Получим уравнение-следствие (х-1) 2 = 9. Откуда х 2 — 2х — 8 = 0, х₁ = — 2, х₂ = 4. Вновь у уравнения-следствия появляется посторонний корень по отношению к исходному уравнению. Преобразовав уравнение (х-1) 2 = 9 к виду (х-4)(х+ 2)=0, получаем постороннее уравнение х + 2 = 0 и посторонний корень -2. Нарушено условие теоремы 5: возводя в квадрат, мы «забыли», что при возведении в квадрат должно выполняться условие х — 1 >0.

в) Рассмотрим уравнение ln (2х — 4) = 1 n (3х — 5). Потенцируя, получим уравнение 2х — 4 = Зх — 5. Откуда х = 1. Проверкой убеждаемся, что 1 является посторонним корнем для исходного уравнения. В данном случае произошло не появление постороннего уравнения, а расширение ОДЗ исходного уравнения. У исходного уравнения ОДЗ: (2; + ), у полученного уравнения ОДЗ — вся числовая прямая. Тем самым не нарушены требования теоремы 6.

6) Выводы. Исходное уравнение преобразуется в процессе решения в уравнение-следствие, значит, необходимо обязательное выполнение проверки всех найденных корней, если: расширилась ОДЗ уравнения; возводились в одну и ту же чётную степень обе части уравнения; выполнялось умножение обеих частей уравнения на одно и тоже выражение с переменной.

1) № 1663; № 1665(а, в); № 1666 (а, б).

2) Переходя к решению уравнений, мы будем стараться учесть следующие два момента. С одной стороны наши решения уравнений должны содержать необходимое теоретическое обоснование нашей деятельности. С другой стороны мы будем учитывать, что в дальнейшем, при решении неравенств, в большинстве случаев от нас потребуется обеспечение равносильности переходов в преобразованиях, и поэтому уже на данном этапе — при решении уравнений, мы будем отрабатывать именно эти навыки, дабы обеспечить преемственность способов деятельности.

Пусть на дано уравнение g ( x ) Возведя в квадрат обе части уравнения, получим уравнение f (х) = g 2 (х) которое можно записать так:

( — g ( x )) ( + g ( x ))=0

Откуда получаем совокупность уравнений: .

Имеем постороннее уравнение, и могут появиться посторонние корни. Следовательно, необходима проверка корней. Если мы захотим выполнить равносильный переход и обойтись без проверки, то исходное уравнение

равносильно смешанной системе:

3) Решим уравнения (двумя способами):

а) ; б );

в) ; г) .

а) Первый способ. Решение. ОДЗ уравнения: х > — 11. После возведения обеих частей уравнения в квадрат, получим уравнение-следствие х 2 -Зх-10 = 0 с корнями — 2 и 5. Оба корня принадлежат ОДЗ уравнения, но это не меняет сути дела и мы вынуждены выполнить проверку корней.

Проверка. Подставив x ₁ = — 2 , получим — неверное равенство, — 2 — посторонний корень.

Подставив х₂ = 5, получим или 4 = 4 — верное равенство, 5 корень исходного уравнения.

а) Второй способ. Решение. Исходное уравнение равносильно системе

или решение системы и исходного

б) Первый способ. Решение. ОДЗ уравнения: . Возведя обе части

уравнения в квадрат и приведя подобные слагаемые, получим уравнение х 2 — х = 0. Откуда x ₁ = 0, х₂ = 1 . Опять оба корня принадлежат ОДЗ уравнения, но будут ли они корнями исходного уравнения ничего сказать нельзя.

Проверка . Подставив x ₁ = 0 , получим — верное равенство, 0— корень исходного уравнения.

Подставив х₂ = 1, получим — верное равенство, 1 — корень исходного уравнения.

или . Откуда решение системы и исходного уравнения 0 и 1.

в) Первый способ. Решение. ОДЗ уравнения: -1 . Возведя обе части уравнения в квадрат и приведя подобные слагаемые, получим уравнение . Откуда x ₁ = 0, х₂ = . Оба корня принадлежат ОДЗ

уравнения. Выполним проверку.

Проверка . Подставив x ₁ = 0 , получим — неверное равенство, 0-посторонний корень.

Подставив х₂ = , получим — неверное равенство, -посторонний корень.

Оба корня принадлежат ОДЗ переменной уравнения, но при этом являются посторонними корнями. Ответ: корней нет.

в) Второй способ. Решение. Исходное уравнение равносильно системе или . Система решений не имеет, значит, и уравнение тоже решений не имеет.

г) Первый способ. Решение. ОДЗ уравнения задаётся решением системы , или которая решений не имеет. Значит, ОДЗ уравнения — пустое множество, уравнение решений не имеет.

г) Второй способ. Решение. Исходное уравнение равносильно системе или Система решений не имеет, значит, и исходное уравнение тоже решений не имеет.

4) № 1676 (а) .

Решение. Произведение двух сомножителей равно нулю, если хотя бы один из сомножителей равен нулю, а второй сомножитель при этом имеет смысл.

Проверим, имеет ли смысл при этих значениях второй сомножитель.

При x ₁ =-3, — имеет смысл, поэтому — 3 — корень уравнения; при х₂ = 3, — не имеет смысла, 3 не является корнем уравнения.

б) , .

Уравнение равносильно системе или

Решением системы является число 1. Так как х 2 — 9 имеет смысл при всех значениях переменной, то 1 является и корнем исходного уравнения.

5) Выводы. При решении иррациональных уравнений — возведении обеих частей уравнения в чётную степень, принадлежность полученных корней ОДЗ уравнения не позволяет сделать вывод, о том являются ли эти корни посторонними или нет. Поэтому выполнение проверки корней обязательно и это этап решения уравнения. Если корень не принадлежит ОДЗ то он, конечно, посторонний корень уравнения. В то же время, записывая систему равносильную уравнению, мы не нарушаем логики решения уравнения: ведь уравнение с пустой ОДЗ равносильно системе, не имеющей решений.

Решить уравнение двумя способами.

I вариант II вариант

§ 55 по учебнику; № 1673 по задачнику (решить двумя способами).