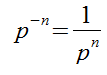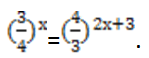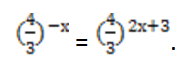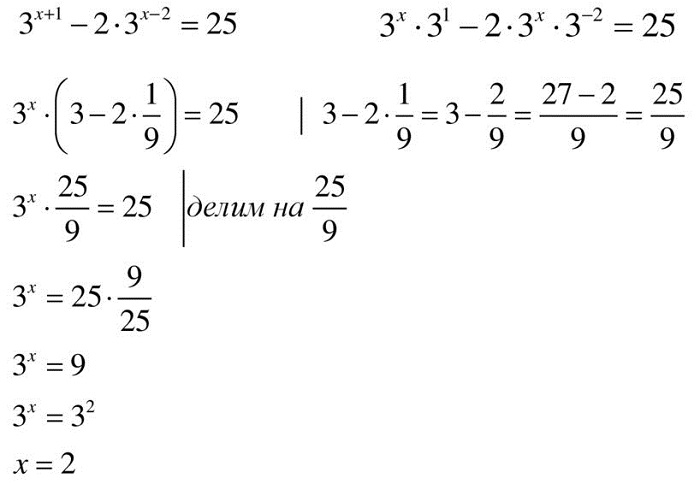Сформулируйте определение простейшего показательного уравнения (4 видео)

Показательные уравнения

О чем эта статья:

6 класс, 7 класс

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Содержание

Определение показательного уравнения
Свойства степеней
Простейшие показательные уравнения
Какие показательные уравнения называют простейшими
Как решать простейшие показательные уравнения? Алгоритм
Теоретическое обоснование
Решение общими методами
Примеры решений
Показательные уравнения — алгоритмы и примеры вычисления
Основные понятия и свойства
Примеры решения показательных уравнений
Задание 1
Задание 2
Задание 3
Задание 4
Задание 5
Задание 6
🔍 Видео

Видео:11 класс, 12 урок, Показательные уравненияСкачать

Определение показательного уравнения

Показательными называются уравнения с показательной функцией f(x) = a х . Другими словами, неизвестная переменная в них может содержаться как в основании степени, так и в ее показателе. Простейшее уравнение такого вида: a х = b, где a > 0, a ≠ 1.

Конечно, далеко не все задачи выглядят так просто, некоторые из них включают тригонометрические, логарифмические и другие конструкции. Но для решения даже простых показательных уравнений нужно вспомнить из курса алгебры за 6–7 класс следующие темы:

Если что-то успело забыться, советуем повторить эти темы перед тем, как читать дальнейший материал.

С точки зрения геометрии показательной функцией называют такую: y = a x , где a > 0 и a ≠ 1. У нее есть одно важное для решения показательных уравнений свойство — это монотонность. При a > 1 такая функция непрерывно возрастает, а при a

Иногда в результате решения будет получаться несколько вариантов ответа, и в таком случае мы должны выбрать тот корень, при котором показательная функция больше нуля.

Свойства степеней

Мы недаром просили повторить свойства степенной функции — на них будет основано решение большей части примеров. Держите небольшую шпаргалку по формулам, которые помогут упрощать сложные показательные уравнения.

Видео:Показательные уравнения. 11 класс.Скачать

Простейшие показательные уравнения

После того, как мы разобрались с вопросом, что такое показательные уравнения, следует остановиться на так называемых простейших показательных уравнениях. Тому есть две причины. Первая – изучение чего-то нового всегда логично начинать с самого простого. Вторая – к простейшим показательным уравнениям часто сводятся решения более сложных показательных уравнений. Так давайте выясним, какие показательные уравнения называют простейшими, и научимся решать простейшие показательные уравнения.

Видео:ПРОСТЕЙШИЙ способ решения Показательных УравненийСкачать

Какие показательные уравнения называют простейшими

простейшими показательными уравнениями называют уравнения a x =b , где a и b – числа, причем a>0 и a≠1 .

В точности так про простейшие показательные уравнения сказано в учебнике Колмогорова [1, с. 229].

Прежде чем привести примеры простейших показательных уравнений, отвечающих этому определению, считаем нужным сказать пару слов об условиях a>0 и a≠1 .

Первое из них объясняется определением степени, ведь степень с действительным показателем мы определили лишь для положительных оснований. Это не означает, что не нужно изучать уравнения a x =b при a и a=0 , ведь они не лишены смысла. Уравнения a x =b при a имеют смысл на множестве целых чисел, а уравнения a x =b при a=0 , то есть, уравнения 0 x =b , имеют смысл на множестве положительных действительных чисел. Решение уравнений a x =b при a имеет свою специфику, с которой лучше разбираться отдельно. Уравнения a x =b при a=0 есть частный случай уравнений, сводящихся к числовым равенствам.

А зачем в определении простейших показательных уравнений второе условие a≠1 ? Это условие исключает из рассмотрения уравнения 1 x =b . Это тоже уравнения, сводящиеся к числовым равенствам.

Итак, дальше в этой статье мы считаем, что a>0 , a≠1 .

Теперь обещанные примеры. Начнем с уравнения 2 x =8 . Это есть уравнение a x =b при a=2 , b=8 , значит, это простейшее показательное уравнение. Аналогично, 3 x =7 , , 2 x =0 , 5 x =−25 – простейшие показательные уравнения.

Еще вспомним, что числа могут быть записаны не только в виде отдельных чисел, но и в виде числовых выражений. Этот факт и данное выше определение позволяют нам утверждать, что уравнения A x =B , где A и В – числовые выражения, причем A>0 , A≠1 , это тоже простейшие показательные уравнения. Так 5 x =5 3 , , – это простейшие показательные уравнения.

Встречаются и немного отличающиеся взгляды на простейшие показательные уравнения. Вот тому пример

Простейшим показательным уравнением является уравнение a x =b , где a и b – данные положительные числа ( a≠1 ), а x – неизвестная величина [2, с. 111].

От первого определения оно отличается тем, что дано ограничение на число b – оно подразумевается положительным. В первом определении про число b ничего не сказано, поэтому, оно подразумевается любым (отрицательным, нулем, положительным). Если придерживаться второго определения, то два из приведенных выше уравнений, а именно, 2 x =0 и 5 x =−25 , не будут простейшими.

Считать или не считать простейшими уравнения a x =b при b=0 и b – судить не нам. Главное – уметь их решать. Давайте научимся это делать.

Видео:Показательные уравнения. Задание 13 | Математика ЕГЭ | УмскулСкачать

Как решать простейшие показательные уравнения? Алгоритм

Судя по названию, простейшие показательные уравнения a x =b , где a и b – числа, причем a>0 , a≠1 , должны решаться легко. Так оно и есть:

Если b или b=0 , то уравнение a x =b не имеет решений.
Если b>0 , то исходное уравнение a x =b нужно преобразовать к виду a x =a c (кроме случаев, когда оно сразу имеет такой вид), откуда очевиден единственный корень x=c .

Например, простейшие показательные уравнения 3 x =−5 и (0,3) x =0 не имеют решений, так как в правой части первого из них находится отрицательное число, а в правой части второго – нуль. А чтобы решить простейшее показательное уравнение 2 x =8 , его нужно преобразовать к виду 2 x =2 3 , что позволяет увидеть его единственное решение x=3 .

После знакомства с логарифмом появляется возможность обходиться без преобразования исходного простейшего показательного уравнения a x =b при b>0 к виду a x =a c , а сразу записывать решение через логарифм как x=log_ab .

Почему решать простейшие показательные уравнения нужно именно так, обоснуем в следующем пункте. А сейчас запишем алгоритм решения простейших показательных уравнений:

Чтобы решить простейшее показательное уравнение a x =b , где a и b – числа, причем a>0 , a≠1 , надо

Убедиться, что перед нами именно простейшее показательное уравнение. Для этого нужно проверить, что уравнение имеет вид a x =b , и убедиться, что a>0 и a≠1 .
Посмотреть, каким числом является b : отрицательным, нулем, или положительным.
Если b или b=0 , то сделать вывод об отсутствии решений.
Если b>0 , то перейти к следующему шагу.
Если b представляет собой степень a c , то перейти к следующему шагу. В противном случае представить число b в виде степени a c , то есть, перейти от исходного уравнения a x =b к уравнению a x =a c .
От равенства степеней a x =a c перейти к равенству их показателей, то есть, к равенству x=c . Это даст единственный корень исходного уравнения.

Видео:Показательные уравнения за 50 минут | Математика ЕГЭ 10 класс | УмскулСкачать

Теоретическое обоснование

Решение показательных уравнений a x =b , где a>0 , a≠1 , b – некоторое число, базируется на следующих двух утверждениях:

Если b=0 или b , то уравнение a x =b не имеет решений.
Если b>0 , то уравнение a x =b имеет единственное решение x=log_ab , где log_ab – логарифм числа b по основанию a . В частности, если число b представляет собой некоторую степень числа a , то есть, b=a c , то единственное решение уравнения есть x=c .

Сразу заметим, что сейчас в школе показательные уравнения обычно изучают до знакомства с логарифмом. По этой причине сначала обходят обращение к логарифму. И делают это так: рассматривают только такие простейшие показательные уравнения, в которых число b представляет собой некоторую степень числа a . То есть, сначала рассматривают уравнения a x =a c , где c – некоторое число. Единственным решением уравнения a x =a c является x=c . А уже после знакомства с логарифмом возвращаются к показательным уравнениям, и уже тогда говорят про единственное решение простейшего показательного уравнения a x =b в виде x=log_ab .

Сейчас мы приведем доказательство этих утверждений, чтобы стало понятно, откуда они произрастают. После этого рассмотрим решения нескольких простейших показательных уравнений, которые покрывают все случаи: и когда b , и когда b=0 , и когда b можно представить в виде степени числа a без использования логарифма, и когда без логарифма не обойтись.

Если b=0 или b , то уравнение a x =b , где a>0 , a≠1 не имеет решений.

Из определения степени вытекает, что если a>0 , то a x >0 при любом значении переменной x . Из этого следует, что ни при каком значении переменной x равенство a x =b не может быть достигнуто, если b=0 или b . Значит, если b=0 или b , то уравнение a x =b не имеет решений, что и требовалось доказать.

Если b>0 , то уравнение a x =b имеет единственное решение x=log_ab , где log_ab – логарифм числа b по основанию a . В частности, если число b представляет собой некоторую степень числа a , то есть, b=a c , то единственное решение уравнения есть x=c .

Доказательство позволяют провести известные свойства показательной функции y=a x , а именно, область значений показательной функции и свойство монотонности.

Для доказательства существования корня у простейшего показательного уравнения a x =b при b>0 нам потребуется известная область значений показательной функции y=a x . Ею является множество всех положительных чисел. Так как у нас по условию b>0 , то b принадлежит области значений показательной функции y=a x . То есть, функция y=a x обязательно принимает значение b . Из этого следует, что уравнение a x =b имеет решение.

Мы доказали, что если b>0 , то простейшее показательное уравнение a x =b обязательно имеет решение. Докажем, что это решение единственное. Для этого обопремся на монотонность показательной функции и воспользуемся методом от противного. Предположим, что кроме корня x₁ уравнение a x =b имеет еще один корень x₂ , отличный от x₁ , то есть, x₁≠x₂ . Так как и x₁ и x₂ – корни уравнения a x =b , то a x₁ =b и a x₂ =b – верные числовые равенства. Свойства числовых равенств позволяют нам проводить почленное вычитание верных числовых равенств. Вычтем из равенства a x₁ =b равенство a x₂ =b , это дает a x₁ −a x₂ =b−b и дальше a x₁ −a x₂ =0 , что то же самое a x₁ =a x₂ . Но из монотонности функции y=a x и из неравенства x₁≠x₂ следует, что либо a x₁ >a x₂ , либо a x₁ x₂ . А это противоречит результату a x₁ =a x₂ . Так доказано, что простейшее показательное уравнение a x =b при b>0 имеет единственный корень.

Итак, мы доказали что уравнение a x =b при b>0 имеет корень, причем единственный. Докажем, что этим корнем является логарифм числа b по основанию a , то есть, x=log_ab . Это напрямую следует из определения логарифма.

Остается показать, что если b=a c , то корнем уравнения a x =b является x=c . Это очевидно. Уравнение a x =b при b=a c имеет вид a x =a c , корень этого уравнения очевиден x=c . Здесь к месту напомнить, что две степени с одинаковыми положительными и не равными единице основаниями равны тогда и только тогда, когда их показатели равны (это известное свойство степеней). К этому же результату мы придем, если будем действовать через логарифмы: x=log_ab – корень уравнения a x =b , при b=a c имеем x=log_ab=log_aa c =с .

Утверждение полностью доказано.

Видео:ПОКАЗАТЕЛЬНЫЕ УРАВНЕНИЯ 10 класс решение показательных уравненийСкачать

Решение общими методами

Алгоритм с его теоретическим обоснованием представляет собой полноценный метод решения простейших показательных уравнений. Однако стоит иметь в виду, что простейшие показательные уравнения можно решать при помощи хорошо известных методов решения уравнений. А именно:

Вывод о том, что простейшее показательное уравнение a x =b при b или b=0 не имеет решений, можно сделать на основании метода оценки.
Преобразование простейшего показательного уравнения a x =b при b>0 к виду a x =a c проводится в соответствии методом решения уравнений через преобразования, а следующий переход к равенству x=c делается в согласии с методом уравнивания показателей, который по сути является методом освобождения от внешней функции.
Простейшее показательное уравнение a x =b при b>0 можно решать и методом логарифмирования, подразумевающим переход от a x =b к log_aa x =log_ab . А следующий переход от уравнения log_aa x =log_ab к x=log_ab , дающий нам конечный результат, проводится в согласии с методом решения уравнений через преобразования.

Видео:Показательные уравнения. Часть 1 из 3. Простейшие (?)Скачать

Примеры решений

В предыдущих пунктах мы разобрали теорию решения простейших показательных уравнений и записали алгоритм. Давайте перейдем к практике, и разберем решения нескольких характерных примеров.

Сначала покажем решения уравнений a x =b , где a>0 , a≠1 , а число b в правой части — отрицательное. Выше мы показали, что такие уравнения не имеют решений.

б)

в)

Теперь покажем решения простейших показательных уравнения с нулями в правых частях. Такие уравнения тоже не имеют решений.

б)

Теперь давайте рассмотрим примеры решения простейших показательных уравнений, отвечающих виду a x =a c . Их единственное решение очевидно: x=c .

Решите показательные уравнения:

а)

б)

в)

г)

В предыдущем примере мы имели дело с очень удобными для решения простейшими показательными уравнениями, имеющими вид a x =a c . Давайте рассмотрим решения чуть более сложных уравнений, которые изначально имеют вид, отличный от a x =a c , но могут быть приведены к нему посредством преобразования числовых выражений, находящихся в правых частях.

б)

в)

г)

Но иногда число или числовое выражение в правой части уравнения невозможно представить в виде степени с нужным основанием без использования логарифма. Так что стоит остановиться на случаях, когда без логарифмов не обойтись.

б)

На простейшие показательные уравнения внешне похожи уравнения a f(x) =b , где f(x) – некоторое выражение с переменной x . Например, 2 x−1 =2 2 , . Про их решение мы поговорим чуть позже. До этого нужно разобрать алгоритм решения показательных уравнений.

Видео:Показательные уравнения — что это такое и как решатьСкачать

Показательные уравнения — алгоритмы и примеры вычисления

Показательные уравнения, как и любые другие, требуют поиска неизвестной переменной. Особенность в том, что она или выражение с ней находится в показателе степени.

Видео:ЕГЭ.Как решать показательные уравнения.Скачать

Основные понятия и свойства

В показательных уравнениях, которые часто называют степенными, в основании находятся исключительно числа. Переменная же есть только в показателе.

Она может быть одна или являться частью выражения. Если она появляется в другом месте, приходится иметь дело с уравнениями смешанного типа.

Школьники знакомятся с простыми вычислениями уже в 7 классе, более сложные решают выпускники и студенты вузов. Если фигурирует несколько переменных и представлено больше одного уравнения, говорят об их системе.

Тогда необходимо выразить одну неизвестную через другую и искать результат методом подстановки. Поэтому умение находить значения, в которые возводят натуральные числа, пригодится на долгие годы.

Изучаются также и показательные функции: она может быть восходящей и нисходящей, в зависимости от значения переменной или выражения.

2 x = 4 – показательное уравнение с иксом в степени;

2 x = x + 12 – смешанное, ведь икс находится также и в основании.

2 – основание, оно должно соответствовать двум условиям, а именно: быть больше нуля и отличаться от единицы;

Если вместо знака «=» используются обозначения «>», « 1 = 9. Если же возвести число в степень ноль, то результат всегда будет одинаковым, а именно, равным единице: 9 0 = 1.

2. Если математическое выражение возводится в отрицательное значение, то его можно заменить дробью, где числитель – единица, а знаменатель первоначальное выражение, но уже в положительной степени. Числитель – значение, находящееся над чертой, знаменатель – под ней. Математически правило записывается в следующем виде:

3. Чтобы возвести число в степень, нужно умножить его на себя такое количество раз, которое равно ее значению, то есть р 5 = р·р·р·р·р.

4. Если нужно умножить два положительных числа, отличных от единицы и равных между собой, то нужно сложить их показатели и возвести в полученное значение основание: p 5 ·p 3 = p 5+3 = p 8 .

5. Когда требуется разделить одно число на другое, имеющие отличные показатели, нужно вычесть из одного другой и возвести в полученное значение неизменное основание: p 9 /p 3 = p 9-3 = p 6 .

6. Если необходимо возвести одну степень в другую, то нужно их перемножить. Само основание при этом остается без изменений. Его нужно возвести в полученное после арифметических действий значение: (p 3 ) 4 = p 3*4 = p 12 .

Применение свойств и правил помогает упростить выражения, быстрее произвести вычисления и получить результат.

Видео:✓ Показательное уравнение | ЕГЭ-2017. Задание 12. Математика. Профильный уровень | Борис ТрушинСкачать

Примеры решения показательных уравнений

Закрепить материал помогут подробные объяснения при решении показательных уравнений. Разъяснения на практике помогут изучить сложные моменты и облегчат усвоение знаний.

Задание 1

Упростить и решить уравнение: 5 3x+14 = 5 7+2x

В обеих частях примера одинаковые основания, значит, можно приравнять математические выражения, находящиеся в показателе. В результате получится:

Путем переноса чисел в одну часть, а переменных в другую, не сложно решить пример. Главное, не забывать менять знак на противоположный, плюс на минус и наоборот:

Задание 2

Выполнить вычисление и найти х:

Основания обеих частей примера – 4, оно не меняется, следовательно, можно воспользоваться изученными свойствами и получить простейшее уравнение:

Задание 3

Упростить и найти значение х:

Дроби в примере разные. Поэтому приравнять их показатели сразу не получится. Но стоит обратить внимание, что числитель одной равен знаменателю другой и наоборот.

Чтобы решить, придется вспомнить о правиле возведения в отрицательную степень, когда выражение представляется в виде дроби. Значит, числитель можно поменять местами со знаменателем.

В показателе при этом появится знак «минус»:

При равных основаниях приравниваются степени: -х = 2х + 3.

Далее придется выполнить простое задание, чтобы найти неизвестную переменную:

Задание 4

Вычислить: (3 x ) 2 = 81.

Можно представить в следующем виде: (3 x ) 2 = 3 4 .

Если воспользоваться изученными свойствами, получается: 3 2x = 3 4 .

Далее выполнить простые действия, чтобы получить результат:

Задание 5

Решить уравнение: 5 x+1 + 7·5 x-2 = 132.

Если воспользоваться свойством степеней, применяемых для умножения значений с одинаковым основанием, можно преобразовать уравнение. Общий множитель прежде всего нужно поставить за скобки, это правило регулярно применяется при решении:

5 x-2 (5 3 + 7) = 132;

Если обе части уравнения разделить или умножить на одно и то же число, результат не изменится. В данном случае необходимо разделить на число 132. Это помогает избавиться от громоздких вычислений, удлиняющих ход решения:

Далее необходимо вспомнить, что любое значение, возведенное в ноль, равно единице:

Остается только приравнять показатели и решить элементарный пример:

Задание 6

Решить показательное уравнение √4 x = 16.

Квадратный корень можно заменить степенью 1/2. Получается, что 4 имеет показатель x/2.

Значит, уравнение преобразуются в следующее:

А дальше необходимо действовать по уже проверенному и закрепленному методу:

Чтобы быстро решать показательные уравнения, нужно знать свойства степеней и умело ими пользоваться на практике. Это позволит легко находить неизвестные переменные. Полученные знания обязательно пригодятся для вычисления более сложных задач.

Существуют онлайн калькуляторы, позволяющие легко и просто решить степенные уравнения. Требуется просто вписать их в ячейку и немного подождать, пока машина справится с подсчетами. Но гораздо интереснее самому произвести арифметические действия и получить верный результат.

Интернет не всегда есть под рукой, а подобные примеры – основа решения более трудных задач, которые могут встретиться на экзамене ЕГЭ по математике. Например, логарифмических. Они могут содержать тригонометрические элементы и объемные алгебраические конструкции.