при всех x ? 0 является функция
Действительно, подставив выражение для y(x) в левую
и в правую часть уравнения
получили тождественное равенство
справедливое при всех x ? 0 и при произвольных значениях константы C.
дифференциальный уравнение показательный радиоактивный
- Уравнение показательного роста. Радиоактивный распад
- Задача 2 (радиоактивный распад)
- Дифференциальные уравнения с разделяющимися переменными и их интегрирование
- п.1. Понятие дифференциального уравнения с разделяющимися переменными
- п.2. Задача Коши
- п.3. Закон радиоактивного распада
- п.4. Зарядка конденсатора
- п.5. Примеры
- 🌟 Видео
Видео:Закон радиоактивного распада. Период полураспадаСкачать
Уравнение показательного роста. Радиоактивный распад
В результате экспериментов, Ф. Содди и Э. Резерфорд вывели закон радиоактивного распада, который описывается дифференциальным уравнением
где N ? количество радиоактивного материала,
л ? положительная константа, зависящая от радиоактивного вещества.
Знак минус в правой части означает, что количество радиоактивного материала N(t) со временем уменьшается (рисунок 1).
Данное уравнение легко решить, и решение имеет вид:
Чтобы определить постоянную C, необходимо указать начальное значение. Если в момент t = 0 количество вещества было N0, то закон радиоактивного распада записывается в виде:
Далее мы введем две полезных величины, вытекающие из данного закона. Периодом полураспада T радиоактивного материала называется время, необходимое для распада половины первоначального количества вещества. Следовательно, в момент T:
Отсюда получаем формулу для периода полураспада:
Среднее время жизни ф радиоактивного атома определяется выражением:
Видно, что период полураспада T и среднее время жизни ф связаны между собой по формуле:
Эти два параметра широко варьируются для различных радиоактивных материалов. Например, период полураспада полония-212 меньше 1 микросекунды, а период полураспада тория-232 превышает миллиард лет! Большой спектр изотопов с различными периодами полураспада был выброшен из атомных реакторов и охлаждающих бассейнов при авариях в Чернобыле и Фукусиме.
Радиоактивный изотоп индий-111 часто используется в радиоизотопной медицинской диагностике и лучевой терапии. Его период полураспада составляет 2,8 дней. Какова была первоначальная масса изотопного вещества, если через две недели осталось 5 г?
Используя закон радиоактивного распада, можно записать:
Решим уравнение относительно N0:
Подставляя известные значения T = 2.8 дней, t = 14 дней и N(t = 14) = 5г, получаем:
Начальная масса изотопа йода составляла 200г. Определить массу йода спустя 30 дней, если период полураспада данного изотопа 8 дней.
Согласно закону радиоактивного распада, масса изотопного вещества зависит от времени следующим образом:
Видео:Об определении решения дифференциального уравненияСкачать
Задача 2 (радиоактивный распад)
Основные понятия
Дифференциальных уравнений
При решении различных задач математики, физики, химии, экономики и других наук часто пользуются математическими моделями в виде уравнений, связывающих независимую переменную, искомую функцию и ее производную. Такие уравнения называются дифференциальными (термин принадлежит Г. Лейбницу, 1676 г.). Решением дифференциального уравнения называется функция, которая при подстановке в уравнение обращает его в тождество.
Так, решением уравнения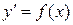 
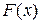
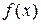
является функция 
— первообразная для функции 
.
Задачи, приводящие к дифференциальным уравнениям
Рассмотрим две физические задачи, решение которых приводит к дифференциальным уравнениям. Но заметим, что при решении задач физического характера, приводящих к дифференциальным уравнениям, основную трудность представляет, как правило, составление самих дифференциальных уравнений. Здесь нет общего метода, и каждая задача требует своего подхода, основанного на знании соответствующего закона физики.
Задача 1 (движение материальной точки).
Материальная точка массы 
замедляет свое движение под действием силы сопротивления среды, пропорциональной квадрату скорости 
. Найти зависимость скорости от времени.
Решение. Примем за независимую переменную время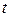 
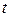
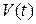
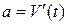
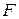
, отсчитываемое от начала замедления движения материальной точки. Тогда скорость точки будет функцией , т.е. 
. Для нахождения 
воспользуемся вторым законом Ньютона (основным законом механики): 
, где 
— есть ускорение движущегося тела, 
— результирующая сила, действующая на тело в процессе движения.
В данном случае 
— коэффициент пропорциональности (знак минус указывает на то, что скорость тела уменьшается). Следовательно, функция является решением дифференциального уравнения
или 
, где — масса тела.
Это же уравнение можно записать так
.
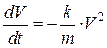
Задача 2 (радиоактивный распад).
Экспериментальным путем установлено, что скорость радиоактивного распада пропорциональна количеству нераспавшегося вещества. Считая, что начальное количество вещества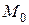 
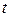
, найти зависимость между количеством нераспавшегося вещества 
и временем .
Решение. Скорость радиоактивного распада равна производной от количества вещества по времени , т.е. 
. Учитывая условие, получаем следующее дифференциальное уравнение
,
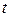
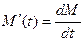
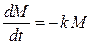
где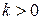 
— коэффициент пропорциональности.
Знак минус берется потому, что с возрастанием 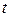количество вещества уменьшается, а значит, производная не положительна.
Можно убедиться, что частным решением данного уравнения является функция
.
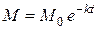
Определение 1.1. Дифференциальным уравнением (ДУ) называется уравнение, связывающее независимую переменную 
, искомую функцию 
и ее производные 
. ДУ записывается так:
.
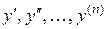
Если искомая (неизвестная) функция зависит от одной переменной, то ДУ называется обыкновенным, в противном случае – ДУ в частных производных.
Определение 1.2. Порядком ДУ называется порядок наивысшей производной, входящей в уравнение.
Например, уравнение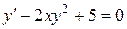 
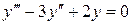
— обыкновенное ДУ первого порядка; уравнение 
— ДУ третьего порядка; 
— ДУ в частных производных первого порядка.
Определение 1.3. Решением ДУ называется функция, которая при подстановке ее вместе с производной в это уравнение превращает его в тождество.
Например, для уравнения 
функции вида 
, 
или 
, где 
— любые постоянные, являются решениями данного уравнения. Например, для уравнения 
функция вида 
, где 
, является решением данного уравнения.
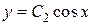
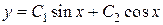
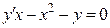
Видео:Нефёдов Н. Н. - Дифференциальные уравнения - ВведениеСкачать
Дифференциальные уравнения с разделяющимися переменными и их интегрирование
п.1. Понятие дифференциального уравнения с разделяющимися переменными
Например:
(y»+y’-4=5cosx) — ДУ второго порядка первой степени
((y’)^3+5y^2=19) – ДУ первого порядка третьей степени
(sqrt=y’x) — ДУ первого порядка первой степени
Самыми простыми для решения будут такие уравнения, у которых можно разделить переменные, т.е. собрать всё, что связано с функцией (y), по одну сторону знака равенства, и всё, что связано с независимой переменной (x), — по другую сторону.
Например:
Уравнение (sqrt=y’x) является уравнением с разделяющимися переменными, т.к. $$ y’=frac<sqrt>=g(x)cdot h(y), text g(x)=frac1x, h(y)=sqrt $$
Алгоритм решения ДУ с разделяющимися переменными
На входе: уравнение первого порядка (y’=f(x,y)), для которого (f(x,y)=g(x)cdot h(y))
Шаг 1. Записать производную в форме Лейбница (y’=frac)
Шаг 2. Преобразовать уравнение
$$ frac=g(x)cdot h(y)Rightarrow frac=g(x)dx $$ Шаг 3. Проинтегрировать левую и правую части уравнения: $$ intfrac=int g(x)dx+C $$ Шаг 4. Результат интегрирования (H(y)=G(x)+C) — общее решение данного уравнения.
На выходе: выражение (H(y)=G(x)+C)
Например:
Решим уравнение (sqrt=y’x)
1) Пусть (xne 0). Тогда: $$ y’=frac<sqrt>Rightarrowfrac=frac<sqrt>Rightarrowfrac<sqrt>=frac $$ Находим интегралы (константу запишем в конце): $$ intfrac<sqrt>=frac<(y+1)^>=frac23sqrt, intfrac=ln|x| $$ Получаем общее решение: $$ frac23sqrt=ln|x|+C, xne 0 $$ 2) Пусть (x=0). Тогда по условию: (sqrt=0Rightarrow y=-1)
Точка (0;-1) – особое решение данного уравнения.
п.2. Задача Коши
Например:
Найдем решение задачи Коши для уравнения (sqrt=y’x) при начальном условии (y(1)=3).
Общее решение нами уже найдено: (frac23sqrt=ln|x|+C) — этим выражением задано бесконечное множество кривых. Решить задачу Коши означает найти единственную кривую, проходящую через точку (1;3), т.е. конкретное значение C для заданных начальных условий.
Подставляем (x=1) и (y=3:frac23sqrt=underbrace_+CRightarrow C=frac23sqrt=frac)
Решение задачи Коши: (frac23sqrt=ln|x|+frac)
Выразим y в явном виде, что всегда приходится делать на практике: $$ sqrt=frac32ln|x|+8Rightarrow y+1=left(frac32ln|x|+8right)^Rightarrow y=left(frac32ln|x|+8right)^-1 $$ Ограничения ОДЗ: ( begin ygeq -1\ frac32ln|x|+8geq 0 end Rightarrow |x|geq -fracRightarrow |x|geq e^<-frac> )
Начальная точка (x=1gt e^<-frac>), требования ОДЗ выполняются.
Т.к. (x=1gt 0) в решении также можно убрать модуль. 
п.3. Закон радиоактивного распада
В многочисленных экспериментах по определению радиоактивности вещества был установлен следующий факт:
| Число распадов ΔN, которые произошли за интервал времени Δt, пропорционально числу атомов N в образце. |
Перейдем к бесконечно малым (dN) и (dt) и запишем соответствующее этому факту дифференциальное уравнение: $$ frac
Полученное ДУ является уравнением с разделяющимися переменными.
Найдем его общее решение: $$ frac=-lambda dtRightarrowintfrac=-lambdaint dtRightarrow ln N=-lambda t+C $$ Пусть в начальный момент времени (t=0) в образце было (N_0) атомов.
Решаем задачу Коши, находим (C: ln N_0=-lambdacdot 0+CRightarrow C=ln N_0)
Подставляем найденное C в общее решение. Получаем: $$ ln N=-lambda N+ln N_0Rightarrow ln N-ln N_0=-lambda tRightarrowlnfrac=-lambda tRightarrowfrac=e^ $$
п.4. Зарядка конденсатора
 | Соберем цепь, состоящую из конденсатора C, резистора R, источника ЭДС E и ключа K. Пусть в начальный момент времени конденсатор разряжен, напряжение на обкладках: (U(0)=0) Замкнем ключ и начнем зарядку конденсатора. |
По закону Ома для замкнутой цепи можем записать: $$ I(R+r_0)+U=varepsilon $$ где (I) — ток в цепи, (I(R+r_0)) – падение напряжения на резисторе и источнике, (U) — напряжение на конденсаторе, (varepsilon) – ЭДС источника.
Ток в цепи равен производной от заряда по времени: $$ I=frac
Начальное условие (U(0)=0). Подставляем: $$ ln(varepsilon-0)=-frac+BRightarrow B=lnvarepsilon $$ Решение задачи Коши: begin ln(varepsilon-U)=-frac+lnvarepsilon\ ln(varepsilon-U)-lnvarepsilon=-frac\ lnfrac=-fracRightarrowfrac=e^<-frac>Rightarrow varepsilon e^<-frac> end
Если внутренне сопротивление источника пренебрежимо мало по сравнению с внешним сопротивлением, (r_0ltlt R), то получаем: $$ u(t)=varepsilonleft(1-e^<-frac>right) $$ При (trightarrow +infty) показатель экспоненты стремится к ((-infty)), а сама экспонента стремится к нулю: (U(trightarrow +infty)=varepsilon(1-e^)), т.е. напряжение на обкладках конденсатора стремится к значению ЭДС источника.
Например:
При (varepsilon=5В, RC=0,01) с график зарядки конденсатора имеет вид:
п.5. Примеры
Пример 1. Решите уравнение:
a) (y’=e^) begin frac=e^xcdot e^yRightarrow e^dy=e^x dxRightarrowint e^dy=int e^x dxRightarrow -e^=e^x+C end (e^=-e^x+C) (на константу, определенную от минус до плюс бесконечности, перемена знака не влияет).
(-y=ln(-e^x+C) )
(y=-ln(C-e^x))
Ответ: (y=ln(C-e^x))
б) (xy+(x+1)y’=0) begin (x+1)y’=-xyRightarrowfrac=-fracRightarrowfrac=-fracdx\ intfrac=ln|y|\ -intfracdx=-intfracdx=-intleft(1-fracright)dx=-x+ln|x+1| end Получаем: (ln|y|=-x+ln|x+1|)
Запишем константу немного по-другому, как (ln C). Это удобно для потенцирования: begin ln|y|-x+ln|x+1|+ln C\ ln|y|-ln C=-x+ln|x+1|\ lnfrac=-x+ln|x+1|\ e^<lnfrac>=e^\ frac yC=e^cdot (x+1)\ y=Ce^(x+1) end При преобразованиях мы делили на ((x+1)) и (y), считая, что (xne -1) и (yne 0). Если подставить (x=-1) в решение, получим (y=0), т.е. эта точка не является особой, она входит в общее решение.
Ответ: (y=Ce^(x+1))
Пример 2*. Найдите решение задачи Коши:
a) (frac+e^y=0, y(1)=0) begin frac=-e^yRightarrowfrac=-x^2e^yRightarrow e^dy=-x^2dx\ int e^dy=-e^, -int x^2dx=-frac end Получаем: begin -e^=-frac+CRightarrow e^=frac+CRightarrow -y=lnleft|frac+Cright|Rightarrow y=-lnleft|frac+Cright| end Общее решение: (y=-lnleft|frac+Cright|)
Решаем задачу Коши. Подставляем начальные условия: $$ 0-lnleft|frac13+Cright|Rightarrowfrac13+C=1Rightarrow C=frac23 $$ Решение задачи Коши: (y=-lnleft|fracright|)
Ответ: (y=-lnleft|fracright|)
б) (x^2(y^2+5)+y^2(x^2+r)y’=0, y(0)=sqrt) begin y^2(x^2+5)y’=-x^2(y^2+5)\ y’=frac=-fracRightarrow fracdy=-fracdx end Используем табличный интеграл: (intfrac=frac1a arctgfrac xa+C) begin intfracdy=intfracdy=intleft(1-fracright)dy=y-5cdotfrac<sqrt>arctgfrac<sqrt>=\ =y-sqrtarctgfrac<sqrt> end Аналогично: (-intfracdx=-x+sqrtarctgfrac<sqrt>)
Общее решение: (y-sqrtarctgfrac<sqrt>=-x+sqrtarctgfrac<sqrt>+C)
Решаем задачу Коши. Подставляем начальные условия: $$ sqrt-sqrtarctg1=-0+0+CRightarrow C=sqrt-frac<pisqrt>=sqrtleft(1-fracpi 4right) $$ Решение задачи Коши: (y-sqrtarctgfrac<sqrt>=-x+sqrtarctgfrac<sqrt>+sqrtleft(1-fracpi 4right))
Ответ: (y-sqrtarctgfrac<sqrt>=-x+sqrtarctgfrac<sqrt>+sqrtleft(1-fracpi 4right))
Пример 3. Найдите массу радиоактивного вещества спустя время, равное четырем периодам полураспада, если начальная масса составляла 64 г.
При радиоактивном распаде атомы одного элемента превращаются в атомы другого, поэтому для массы вещества справедлив тот же закон, что и для количества атомов этого вещества: $$ m(t)=m_0 e^ $$ Период полураспада – это время, за которое масса уменьшается в 2 раза: $$ frac<mleft(T_right)>=frac12 $$ За время, равное 4 периодам полураспада, масса уменьшится: $$ frac<mleft(4T_right)>=left(frac12right)^4=frac $$ в 16 раз.
Получаем: $$ mleft(4T_right)=frac, mleft(4T_right)=frac=4 text $$ Ответ: 4 г
Пример 4. Выведите зависимость (U(t)) на обкладках конденсатора при его разрядке в RC-цепи.
 | Разрядка конденсатора происходит в цепи без источника ЭДС. Пусть в начальный момент заряд на обкладках (U(0)=U_0.) Замкнем ключ и начнем разрядку конденсатора. |
По закону Ома для замкнутой цепи: $$ IR+U=0 $$ Ток в цепи равен производной от заряда по времени: $$ I=frac
Начальное условие (U(0)=0). Подставляем: $$ ln U_0=-frac+BRightarrow B=ln U_0 $$ Решение задачи Коши: begin ln U=-frac+ln U_0Rightarrowln U-ln U_0=-fracRightarrow lnfrac=-frac\ frac=e^<-frac> end
| Изменение напряжение на обкладках конденсатора при разрядке: $$ U(t)=U_0 e^<-frac> $$ |
Например, (при U_0=5В, RC=0,01 с) график разрядки конденсатора имеет вид:
🌟 Видео
Лекции по дифференциальным уравнениям. Обыкновенные дифференциальные уравнения.Скачать
Урок 469. Задачи на закон радиоактивного распадаСкачать
Закон радиоактивного распада. 11 класс.Скачать
Общие понятия дифференциальных уравнений. Разделение переменных | Лекция 13 | МатАн | СтримСкачать
Урок 468. Закон радиоактивного распадаСкачать
Дифференциальное уравнение Лагранжа II рода. Расчет механической системы.Скачать
ОДУ. 1 Понятие ОДУ. Уравнения с разделяющимися переменными. Однородные уравненияСкачать
Дифференциальные уравнения высших порядков (Шишкин Г.А.) - 2 обзорная лекцияСкачать
Урок 327. Гармонические колебанияСкачать
Дифференциальные уравнения, 1 урок, Дифференциальные уравнения. Основные понятияСкачать
Дифференциальные уравнения, ПМИ – лекция 1Скачать
Общее, частное и особое решение ДУ. ПримерСкачать
Обыкновенные дифференциальные уравнения с дискретным временем и рекуррентные последовательностиСкачать
Лукьяненко Д. В. - Дифференциальные уравнения - Лекция 1Скачать
Экстремальные задачи и дифференциальные уравнения. Запись вебинара от 1.02.23Скачать
Жизнь, смерть и дифференциальные уравненияСкачать
