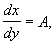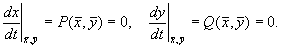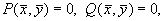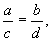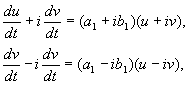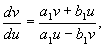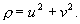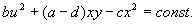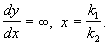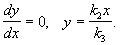Седло узел фокус дифференциальные уравнения (5 видео)

ЛЕКЦИЯ 4

Модели, описываемые системами двух автономных дифференциальных уравнений.

Фазовая плоскость. Фазовый портрет. Метод изоклин. Главные изоклины. Устойчивость стационарного состояния. Линейные системы. Типы особых точек: узел, седло, фокус, центр. Пример: химические реакции первого порядка.

Наиболее интересные результаты по качественному моделированию свойств биологических систем получены на моделях из двух дифференциальных уравнений, которые допускают качественное исследование с помощью метода фазовой плоскости. Рассмотрим систему двух автономных обыкновенных дифференциальных уравнений общего вида

(4.1)

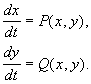
P(x,y), Q(x,y) — непрерывные функции, определенные в некоторой области G евклидовой плоскости ( x,y ‑ декартовы координаты) и имеющие в этой области непрерывные производные порядка не ниже первого.

Область G может быть как неограниченной, так и ограниченной. Если переменные x, y имеют конкретный биологический смысл (концентрации веществ, численности видов) чаще всего область G представляет собой положительный квадрант правой полуплоскости:

Концентрации веществ или численности видов также могут быть ограничены сверху объемом сосуда или площадью ареала обитания. Тогда область значений переменных имеет вид:

Переменные x, y во времени изменяются в соответствии с системой уравнений (4.1), так что каждому состоянию системы соответствует пара значений переменных ( x, y) .

Изображающая точка на фазовой плоскости

Седло узел фокус дифференциальные уравнения

Обратно, каждой паре переменных ( x, y) соответствует определенное состояние системы.

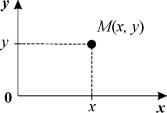
Рассмотрим плоскость с осями координат, на которых отложены значения переменных x,y. Каждая точка М этой плоскости соответствует определенному состоянию системы. Такая плоскость носит название фазовой плоскости и изображает совокупность всех состояний системы. Точка М(x,y) называется изображающей или представляющей точкой.

Пусть в начальный момент времени t=t₀ координаты изображающей точки М₀( x( t₀) , y( t₀)) . В каждый следующий момент времени t изображающая точка будет смещаться в соответствии с изменениями значений переменных x( t) , y( t) . Совокупность точек М( x( t) , y(t)) на фазовой плоскости, положение которых соответствует состояниям системы в процессе изменения во времени переменных x(t), y(t) согласно уравнениям (4.1), называется фазовой траекторией.

Совокупность фазовых траекторий при различных начальных значениях переменных дает легко обозримый «портрет» системы. Построение фазового портрета позволяет сделать выводы о характере изменений переменных x, y без знания аналитических решений исходной системы уравнений (4.1).

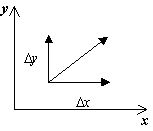
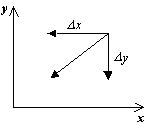
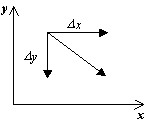
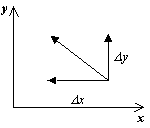
Для изображения фазового портрета необходимо построить векторное поле направлений траекторий системы в каждой точке фазовой плоскости. Задавая приращение D t>0, получим соответствующие приращения D x и D y из выражений:

Направление вектора dy/dx в точке ( x, y) зависит от знака функций P(x, y), Q(x, y) и может быть задано таблицей:

Задача построения векторного поля упрощается, если получить выражение для фазовых траекторий в аналитическом виде. Для этого разделим второе из уравнений системы (4.1) на первое:

. (4.2)

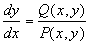
Решение этого уравнения y = y( x, c) , или в неявном виде F( x,y) =c, где с – постоянная интегрирования, дает семейство интегральных кривых уравнения (4.2) ‑ фазовых траекторий системы (4.1) на плоскости x, y.

Для построения фазового портрета пользуются методом изоклин – на фазовой плоскости наносят линии, которые пересекают интегральные кривые под одним определенным углом. Уравнение изоклин легко получить из (4.2). Положим

где А – определенная постоянная величина. Значение А представляет собой тангенс угла наклона касательной к фазовой траектории и может принимать значения от – ¥ до + ¥ . Подставляя вместо dy/dx в (4.2) величину А получим уравнение изоклин:

. (4.3)

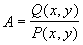
Уравнение (4.3) определяет в каждой точке плоскости единственную касательную к соответствующей интегральной кривой за исключением точки, где P (x,y) = 0, Q ( x,y) = 0, в которой направление касательной становится неопределенным, так как при этом становится неопределенным значение производной:

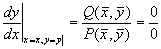
Эта точка является точкой пересечения всех изоклин – особой точкой. В ней одновременно обращаются в нуль производные по времени переменных x и y.

Таким образом, в особой точке скорости изменения переменных равны нулю. Следовательно, особая точка дифференциальных уравнений фазовых траекторий (4.2) соответствует стационарному состоянию системы (4.1), а ее координаты – суть стационарные значения переменных x, y.

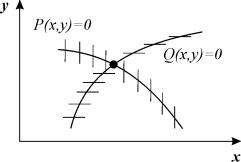
Особый интерес представляют главные изоклины:

dy/dx=0, P ( x,y) =0 – изоклина горизонтальных касательных и

dy/dx= ¥ , Q ( x,y) =0 – изоклина вертикальных касательных.

Построив главные изоклины и найдя точку их пересечения (x,y), координаты которой удовлетворяют условиям:

мы найдем тем самым точку пересечения всех изоклин фазовой плоскости, в которой направление касательных к фазовым траекториям неопределенно. Это – особая точка, которая соответствует стационарному состоянию системы (рис. 4.2).

Система (4.1) обладает столькими стационарными состояниями, сколько точек пересечения главных изоклин имеется на фазовой плоскости.

Каждая фазовая траектория соответствует совокупности движений динамической системы, проходящих через одни и те же состояния и отличающихся друг от друга только началом отсчета времени.

Рис. 4.2. Пересечение главных изоклин на фазовой плоскости.

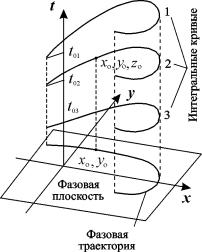
Таким образом, фазовые траектории системы – это проекции интегральных кривых в пространстве всех трех измерений x, y, t на плоскость x, y (рис.4.3).

Рис. 4.3. Траектории системы в пространстве ( x, y, t).

Если условия теоремы Коши выполнены, то через каждую точку пространства x, y, t проходит единственная интегральная кривая. То же справедливо, благодаря автономности, для фазовых траекторий: через каждую точку фазовой плоскости проходит единственная фазовая траектория.

Устойчивость стационарного состояния

Пусть система находится в состоянии равновесия.

Тогда изображающая точка находится в одной из особых точек системы, в которых по определению:

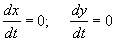
Устойчива или нет особая точка, определяется тем, уйдет или нет изображающая точка при малом отклонении от стационарного состояния. Применительно к системе из двух уравнений определение устойчивости на языке e , d выглядит следующим образом.

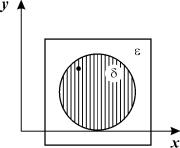
Состояние равновесия устойчиво, если для любой заданной области отклонений от состояния равновесия ( e ) можно указать область d ( e ) , окружающую состояние равновесия и обладающую тем свойством, что ни одна траектория, которая начинается внутри области d , никогда не достигнет границы e . (рис. 4.4)

Иллюстрация к определению устойчивости области e и d на плоскости ( x,y)

Для большого класса систем – грубых систем – характер поведения которых не меняется при малом изменении вида уравнений, информацию о типе поведения в окрестности стационарного состояния можно получить, исследуя не исходную, а упрощенную линеаризованную систему.

Рассмотрим систему двух линейных уравнений:

. (4.4)

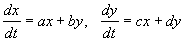
Здесь a, b, c, d — константы, x, y ‑ декартовы координаты на фазовой плоскости.

Общее решение будем искать в виде:

. (4.5)

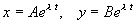
Подставим эти выражения в (4.4) и сократим на e l t :

(4.6)

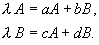
Алгебраическая система уравнений (4.6) с неизвестными A, B имеет ненулевое решение лишь в том случае, если ее определитель, составленный из коэффициентов при неизвестных, равен нулю:

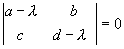
Раскрывая этот определитель, получим характеристическое уравнение системы:

. (4.7)

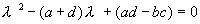
Решение этого уравнения дает значения показателя l _1,2 , при которых возможны ненулевые для A и B решения уравнения (4.6). Эти значения суть

. (4.8)

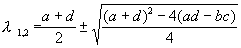
Если подкоренное выражение отрицательно, то l _1,2 комплексно сопряженные числа. Предположим, что оба корня уравнения (4.7) имеют отличные от нуля действительные части и что нет кратных корней. Тогда общее решение системы (4.4) можно представить в виде линейной комбинации экспонент с показателями l ₁ , l ₂ :

_(4.9)

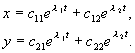
Для анализа характера возможных траекторий системы на фазовой плоскости используем линейное однородное преобразование координат, которое позволит привести систему к каноническому виду:

, (4.10)

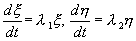
допускающее более удобное представление на фазовой плоскости по сравнению с исходной системой (4.4). Введем новые координаты ξ , η по формулам:

(4.1)

Из курса линейной алгебры известно, что в случае неравенства нулю действительных частей l ₁ , l ₂ исходную систему (4.4) при помощи преобразований (4.11) всегда можно преобразовать к каноническому виду (4.10) и изучать ее поведение на фазовой плоскости ξ , η . Рассмотрим различные случаи, которые могут здесь представиться.

Корни λ ₁ , λ ₂ – действительны и одного знака

В этом случае коэффициенты преобразования действительны, мы переходим от действительной плоскости x,y к действительной плоскости ξ, η. Разделив второе из уравнений (4.10) на первое, получим :

. (4.12)

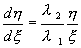
Интегрируя это уравнение, находим :

, где . (4.13)

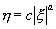
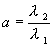
Условимся понимать под λ ₂ корень характеристического уравнения с большим модулем, что не нарушает общности нашего рассуждения. Тогда, поскольку в рассматриваемом случае корни λ ₁ , λ ₂ – действительны и одного знака, a >1 , и мы имеем дело с интегральными кривыми параболического типа.

Все интегральные кривые (кроме оси η, которой соответствует 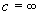) касаются в начале координат оси ξ, которая также является интегральной кривой уравнения (4.11). Начало координат является особой точкой.

Выясним теперь направление движений изображающей точки вдоль фазовых траекторий. Если λ ₁ , λ ₂ – отрицательны, то, как видно из уравнений (4.10), |ξ|, |η| убывают с течением времени. Изображающая точка приближается к началу координат, никогда, однако, не достигая его. В противном случае это противоречило бы теореме Коши, которая утверждает, что через каждую точку фазовой плоскости проходит лишь одна фазовая траектория.

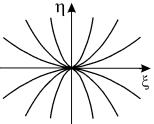
Такая особая точка, через которую проходят интегральные кривые, подобно тому, как семейство парабол 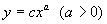проходит через начало координат, носит название узла (рис. 4.5)

Рис. 4.5. Особая точка типа узел на плоскости канонических координат ξ, η

Состояние равновесия типа узел при λ ₁ , λ ₂ 0 устойчиво по Ляпунову, так как изображающая точка по всем интегральным кривым движется по направлению к началу координат. Это устойчивый узел. Если же λ ₁ , λ ₂ > 0, то |ξ|, |η| возрастают с течением времени и изображающая точка удаляется от начала координат. В этом случае особая точка – неустойчивый узел .

На фазовой плоскости x, y общий качественный характер поведения интегральных кривых сохранится, но касательные к интегральным кривым не будут совпадать с осями координат. Угол наклона этих касательных будет определяться соотношением коэффициентов α , β , γ , δ в уравнениях (4.11).

Корни λ ₁ , λ ₂ – действительны и разных знаков.

Преобразование от координат x,y к координатам ξ, η опять действительное. Уравнения для канонических переменных снова имеют вид (4.10), но теперь знаки λ ₁ , λ ₂ различны. Уравнение фазовых траекторий имеет вид :

где , (4.14)

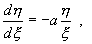
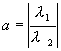
Интегрируя (4.14), находим

(4.15)

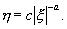
Это уравнение определяет семейство кривых гиперболического типа, где обе оси координат – асимптоты (при a=1 мы имели бы семейство равнобочных гипербол) . Оси координат и в этом случае являются интегральными кривыми – это будут единственные интегральные кривые, проходящие через начало координат. Каждая из них состоит из трех фазовых траекторий : из двух движений к состоянию равновесия (или от состояния равновесия) и из состояния равновесия. Все остальные интегральные кривые – суть гиперболы, не проходящие через начало координат (рис. 4.6) Такая особая точка носит название «седло ». Линии уровня вблизи горной седловины ведут себя подобно фазовым траекториям в окрестности седла.

Рис. 4.6. Особая точка типа седло на плоскости канонических координат ξ , η

Рассмотрим характер движения изображающей точки по фазовым траекториям вблизи состояния равновесия. Пусть, например, λ ₁ >0 , λ ₂ . Тогда изображающая точка, помещенная на оси ξ, будет удаляться от начала координат, а помещенная на оси η – будет неограниченно приближаться к началу координат , не достигая его за конечное время . Где бы ни находилась изображающая точка в начальный момент (за исключением особой точки и точек на асимптоте η =0), она в конечном счете будет удаляться от состояния равновесия, даже если в начале она движется по одной из интегральных кривых по направлению к особой точке .

Очевидно, что особая точка типа седла всегда неустойчива . Только при специально выбранных начальных условиях на асимптоте η =0 система будет приближаться к состоянию равновесия. Однако это не противоречит утверждению о неустойчивости системы. Если считать , что все начальные состояния системы на фазовой плоскости равновероятны, то вероятность такого начального состояния, которое соответствует движению по направлению к особой точке, равна нулю. Поэтому всякое реальное движение будет удалять систему от состояния равновесия. Переходя обратно к координатам x,y, мы получим ту же качественную картину характера движения траекторий вокруг начала координат.

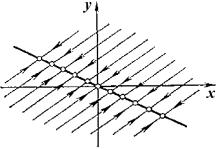
Пограничным между рассмотренными случаями узла и седла является случай, когда один из характеристических показателей, например λ ₁ , обращается в нуль, что имеет место, когда определитель системы – выражение ad-bc=0 (см. формулу 4.8 ). В этом случае коэффициенты правых частей уравнений (4.4) пропорциональны друг другу :

и система имеет своими состояниями равновесия все точки прямой :

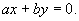
Остальные интегральные кривые представляют собой семейство параллельных прямых с угловым коэффициентом 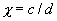, по которым изображающие точки либо приближаются к состоянию равновесия, либо удаляются от него в зависимости от знака второго корня характеристического уравнения λ ₂ = a+d. (Рис.4. 7 ) В этом случае координаты состояния равновесия зависят от начального значения переменных.

Рис. 4.7. Фазовый портрет системы, один из характеристических корней которой равен нулю, а второй отрицателен.

В этом случае при действительных x и y мы будем иметь комплексные сопряженные ξ , η ( 4.10) . Однако , вводя еще одно промежуточное преобразование, можно и в этом случае свести рассмотрение к действительному линейному однородному преобразованию. Положим :

(4.16)

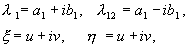
где a,b, и u,v – действительные величины. Можно показать, что преобразование от x,y к u,v является при наших предположениях действительным, линейным, однородным с детерминантом, отличным от нуля. В силу уравнений (4.10, 4.16) имеем :

(4.17)

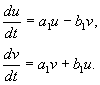
Разделив второе из уравнений на первое , получим :

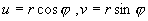
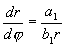
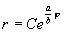
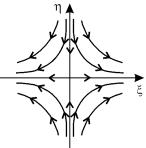
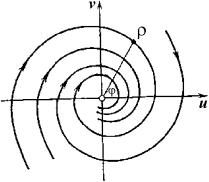
которое легче интегрируется , если перейти к полярной системе координат ( r, φ ) . После подстановки получим , откуда :

. (4.18)

Таким образом, на фазовой плоскости u, v мы имеем дело с семейством логарифмических спиралей, каждая из которых имеет асимптотическую точку в начале координат. Особая точка, которая является асимптотической точкой всех интегральных кривых, имеющих вид спиралей , вложенных друг в друга, называется фокусом ( рис.4.8 ) .

Рис. 4.8. Фазовый портрет системы в окрестности особой точки типа фокус на плоскости координат u, v .

Рассмотрим характер движения изображающей точки по фазовым траекториям. Умножая первое из уравнений (4.17) на u , а второе на v и складывая , получаем :

где

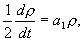
Пусть a ₁ 0 ( a ₁ = Re λ ) . Изображающая точка тогда непрерывно приближается к началу координат, не достигая его в конечное время. Это означает, что фазовые траектории представляют собой скручивающиеся спирали и соответствуют затухающим колебаниям переменных. Это – устойчивый фокус .

В случае устойчивого фокуса, как и в случае устойчивого узла, выполнено не только условие Ляпунова, но и более жесткое требование. Именно, при любых начальных отклонениях система по прошествии времени вернется как угодно близко к положению равновесия. Такая устойчивость, при которой начальные отклонения не только не нарастают, но затухают, стремясь к нулю, называют абсолютной устойчивостью .

Если в формуле (4.18) a₁ >0 , то изображающая точка удаляется от начала координат, и мы имеем дело с неустойчивым фокусом . При переходе от плоскости u,v к фазовой плоскости x , y спирали также останутся спиралями, однако будут деформированы.

Рассмотрим теперь случай, когда a ₁ =0 . Фазовыми траекториями на плоскости u, v будут окружности 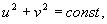которым на плоскости x,y соответствуют эллипсы :

Таким образом, при a₁ =0 через особую точку x= 0 , y=0 не проходит ни одна интегральная кривая. Такая изолированная особая точка, вблизи которой интегральные кривые представляют собой замкнутые кривые, в частности, эллипсы, вложенные друг в друга и охватывающие особую точку, называется центром.

Таким образом, возможны шесть типов состояния равновесия в зависимости от характера корней характеристического уравнения (4.7). Вид фазовых траекторий на плоскости x, y для этих шести случаев изображен на рис. 4.9.

Рис. 4.9. Типы фазовых портретов в окрестности стационарного состояния для системы линейных уравнений (4.4).

Пять типов состояния равновесия грубые, их характер не изменяется при достаточно малых изменениях правых частей уравнений (4.4). При этом малыми должны быть изменения не только правых частей, но и их производных первого порядка. Шестое состояние равновесия – центр – негрубое. При малых изменениях параметров правой части уравнений он переходит в устойчивый или неустойчивый фокус.

Содержание

Бифуркационная диаграмма
Седло узел фокус дифференциальные уравнения
Простейшие типы точек покоя
🔍 Видео

Видео:Особые точки 1 Узел, седло, дикритический узелСкачать

Бифуркационная диаграмма

. (4.11)

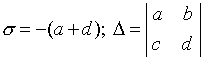
Тогда характеристическое уравнение запишется в виде:

. (4.12)

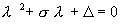
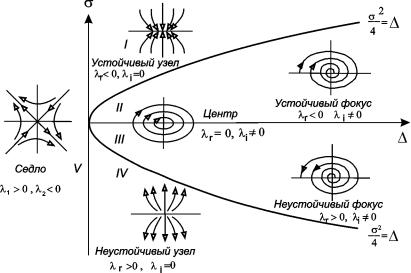
Рассмотрим плоскость с прямоугольными декартовыми координатами s , D и отметим на ней области, соответствующие тому или иному типу состояния равновесия, который определяется характером корней характеристического уравнения

. (4.13)

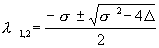
Условием устойчивости состояния равновесия будет наличие отрицательной действительной части у l ₁ и l ₂ . Необходимое и достаточное условие этого – выполнение неравенств s > 0, D > 0 . На диаграмме (4.15) этому условию соответствуют точки, расположенные в первой четверти плоскости параметров. Особая точка будет фокусом, если l ₁ и l ₂ комплексны. Этому условию соответствуют те точки плоскости, для которых 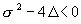, т.е. точки между двумя ветвями параболы s 2 = 4 D . Точки полуоси s = 0, D >0, соответствуют состояниям равновесия типа центр. Аналогично, l ₁ и l ₂ — действительны, но разных знаков, т.е. особая точка будет седлом, если D , и т.д. В итоге мы получим диаграмму разбиения плоскости параметров s , D , на области, соответствующие различным типам состояния равновесия.

Рис. 4.10. Бифуркационная диаграмма

для системы линейных уравнений 4.4

Если коэффициенты линейной системы a, b, c, d зависят от некоторого параметра, то при изменении этого параметра будут меняться и величины s , D . При переходе через границы характер фазового портрета качественно меняется. Поэтому такие границы называются бифуркационными – по разные стороны от границы система имеет два топологически различных фазовых портрета и, соответственно два разных типа поведения.

На диаграмме видно, как могут проходить такие изменения. Если исключить особые случаи – начало координат, – то легко видеть, что седло может переходить в узел, устойчивый или неустойчивый при пересечении оси ординат. Устойчивый узел может перейти либо в седло, либо в устойчивый фокус, и т.д. Отметим, что переходы устойчивый узел – устойчивый фокус и неустойчивый узел – неустойчивый фокус не являются бифуркационными, так как топология фазового пространства при этом не меняется. Более подробно мы поговорим о топологии фазового пространства и бифуркационных переходах в лекции 6.

При бифуркационных переходах меняется характер устойчивости особой точки. Например, устойчивый фокус через центр может переходить в неустойчивый фокус. Эта бифуркация называется бифуркацией Андронова-Хопфа по именам исследовавших ее ученых. При этой бифуркации в нелинейных системах происходит рождение предельного цикла, и система становится автоколебательной (см. лекцию 8).

Пример. Система линейных химических реакций

Вещество Х притекает извне с постоянной скоростью, превращается в вещество Y и со скоростью, пропорциональной концентрации вещества Y, выводится из сферы реакции. Все реакции имеют первый порядок, за исключением притока вещества извне, имеющего нулевой порядок. Схема реакций имеет вид:

(4.14)

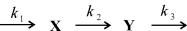
и описывается системой уравнений:

(4.15)

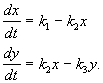
Стационарные концентрации получим, приравняв правые части нулю:

. (4.16)

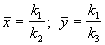
Рассмотрим фазовый портрет системы. Разделим второе уравнение системы (4.16) на первое. Получим:

. (4.17)

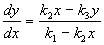
Уравнение (4.17) определяет поведение переменных на фазовой плоскости. Построим фазовый портрет этой системы. Сначала нарисуем главные изоклины на фазовой плоскости. Уравнение изоклины вертикальных касательных:

Уравнение изоклины горизонтальных касательных:

Особая точка (стационарное состояние) лежит на пересечении главных изоклин.

Теперь определим, под каким углом пересекаются координатные оси интегральными кривыми.

Если x=0, то .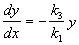

Таким образом, тангенс угла наклона касательной к интегральным кривым y=y(x), пересекающим ось ординат x=0, отрицателен в верхней полуплоскости (вспомним, что переменные x, y имеют значения концентраций, и поэтому нас интересует только правый верхний квадрант фазовой плоскости). При этом величина тангенса угла наклона касательной увеличивается с удалением от начала координат.

Рассмотрим ось y=0 . В месте пересечения этой оси интегральными кривыми они описываются уравнением

При тангенс угла наклона интегральных кривых, пересекающих ось абсцисс, положителен и увеличивается от нуля до бесконечности с увеличением x.

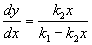
при .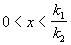

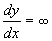
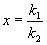
Затем при дальнейшем увеличении тангенс угла наклона уменьшается по абсолютной величине, оставаясь отрицательным и стремится к -1 при x ® ¥ . Зная направление касательных к интегральным кривым на главных изоклинах и на осях координат, легко построить всю картину фазовых траекторий.

Рис. 4.12. Фазовый портрет системы линейных химических реакций (4.15)

Видео:Асташова И. В. - Дифференциальные уравнения. Часть 2 - Фазовый портретСкачать

Седло узел фокус дифференциальные уравнения

Рассмотрим автономную систему второго порядка:

Название автономная система оправдано тем, что решение само управляет своим изменением, поскольку производные dx₁ /dt и dx₂ /dt зависят только от x₁ и x₂ и не зависят от t.

Обозначим
и .
Пусть — решение автономной системы второго порядка. Тогда уравнения

задают в параметрической форме кривую на плоскости . Эта кривая называется фазовой кривой или фазовой траекторией системы.Плоскость, на которой расположены фазовые траектории называется фазовой плоскостью автономной системы.

Точка , в которой правая часть системы обращается в нуль, , называется положением равновесия системы. Положение равновесия называют также точкой покоя автономной системы.

Точка покоя называется устойчивой по Ляпунову, если:
1) существует такое , что для при существует решение задачи Коши с начальным условиям ;
2) для всякого существует такое , что если и , то при всех .
Устойчивая точка покоя называется асимптотически устойчивой, если
при достаточно малых .

Очевидно, что линейная автономная система

имеет единственную точку покоя: x₁(t) = 0, x₂(t) = 0, при всех . При этом характер точки покоя (0, 0) (ее устойчивость, асимптотическую устойчивость, неустойчивость) можно установить по значениям собственных чисел l₁ и l₂ матрицы системы.
А именно, пусть l₁ и l₂ — собственные значения матрицыA исследуемой системы:

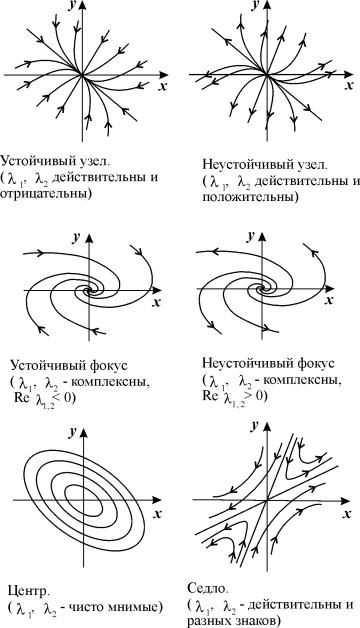
если l₁ и l₂— действительные отрицательные числа, то точка покоя устойчива и называется устойчивым узлом (пример 1);
если l₁ и l₂ — действительные положительные числа, то точка покоя неустойчива и называется неустойчивым узлом (пример 2);
если l₁ и l₂ — действительные числа, имеющие разные знаки, то точка покоя неустойчива и называется седлом (пример 3);
если l₁ и l₂ — комплексные числа, l_1,2 =Rell ± Imll и Rel не превышает нуля, то точка покоя устойчива, точнее, при Rel =0 точка устойчива, но не асимптотически устойчива и называется центром (пример 4), при Rel 0, то точка покоя неустойчива и называется неустойчивым фокусом (пример 6);
если l₁ = l₂ — отличные от нуля действительные числа, то точка покоя — узел специального вида, называемый диакритическим, устойчивым при отрицательных l₁ = l₂ и неустойчивым при положительных l₁ = l₂ (пример 7);
если l₁ = 0 и l₂ № 0, то существует прямая, проходящая через начало координат, все точки которой являются точками покоя (пример 8);
если l₁ = l₂ = 0, то все точки плоскости являются точками покоя.

ПРИМЕР 1. Поведение решений в окрестности устойчивого узла.

ПРИМЕР 2. Поведение решений в окрестности неустойчивого узла.

ПРИМЕР 3. Поведение решений в окрестности седла.

ПРИМЕР 4. Поведение решений в окрестности центра.

ПРИМЕР 5. Поведение решений в окрестности устойчивого фокуса.

ПРИМЕР 6. Поведение решений в окрестности неустойчивого фокуса.

ПРИМЕР 7. Поведение решений в окрестности диакритического узла.

ПРИМЕР 8. Вырожденный случай. Прямая, состоящая из точек покоя.

Исправляем ошибки: Нашли опечатку? Выделите ее мышкой и нажмите Ctrl+Enter

Видео:Асташова И. В. - Дифференциальные уравнения. Часть 2 - Лекция 11Скачать

Простейшие типы точек покоя

Пусть имеем систему двух линейных однородных дифференциальных уравнений с постоянными коэффициентами причем

Точка , в которой правые части уравнений системы (1) обращаются в ноль, называется точкой покоя системы (1).

Для исследования точки покоя системы (1) надо составить характеристическое уравнение

и найти его корни и .

Возможны следующие случаи.

1. Корни характеристического уравнения (2) вещественные и разные:

а) . Точка покоя асимптотически устойчива (устойчивый узел, рис. 32);

б) 0,,lambda_2>0″ png;base64,iVBORw0KGgoAAAANSUhEUgAAAH4AAAATCAMAAABhl0k+AAAAM1BMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAADbQS4qAAAAEHRSTlMAMWHQwCEQA0GageBx8LFRDpCt4AAAAbhJREFUSMfFVldyxCAMpUei6v6nDQZcFsvZkMwk/vDs2KxeUbMQ/34p493KeQnMQzRlJYYDefyOhAvgOmNQ9+eG5ILigKiP8yl8/5/BVwp0N6AsaICNqg+750isc8i4rMhuUs39Da8BuMRmXW+Wdg8ly/zDorkRyNTvt6AfDxqUQTs/o8ae8uFoYk2qBPSUZt3gPeO+fHIfZgIw4A+7kJR4IOBfCdAj/JOGRuDFRiB/hup1M4xgqtd5fcnfDs/QHRosMNTkNY8zvAyhJdNnYps0av9evdJNA2DJxn1ZSNDTtMPLVCLFRpz4Nj3hwxO80k5vGkwULsV7jFpGZcp9GuiqdoHuL96Zb6jf52qOSYqmwSDXl/Y6Fd2ANx0dWytZFr6Cq6uVsff9VrSXuVnzLsWuoYaf1MPUwbr3fWzouY8TZODvjeeSHxND0mnBqLquQXg9Nx4wsysm25i4c2i9wltuj1SzlN6o2nAUgByN0GtK4dWuwowdgSGOxWHHWQtuhs/A9oGKw3V/vN/TIOXWY1XZxXfLBbGxOG4XrGzNzO1paQCK/9HmN5rMwt5ijwaql/qDzxR0vw7xCYY/D3jyG++NAAAAAElFTkSuQmCC» style=»vertical-align: middle;» />. Точка покоя неустойчива (неустойчивый узел, рис. 33);

в) 0,,lambda_2 . Точка покоя неустойчива (седло, рис. 34).

2. Корни характеристического уравнения (2) комплексные:

а) . Точка покоя асимптотически устойчива (устойчивый фокус, рис.35);

qne0″ png;base64,iVBORw0KGgoAAAANSUhEUgAAAGoAAAAVCAMAAACZi4uxAAAAM1BMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAADbQS4qAAAAEHRSTlMAYSHAEJnpQYEB0DHBcbFSUNy43AAAAbpJREFUSMfVVcmShCAMFQKBsJn//9phUTvYdpfW1ByGg5ZWyPMtxGX570v/arN7sF0X+RQdPUGy6JM1d6uLE0BoLaonSBUm2ZvVTpAy6Cscu6s6r97p9vpF8U0NQdRlblqEclVnfMhnpVbO7WP5ng5Osk9MxzVCMdGC6GJU8DOY7wI49m9tFZTo8vwuCVKEG1RrEAwGawzKelLB6guodFYAQt3JeU9aXwraddtO/IKqbBGbvmGyaAazH6B6WizHTWbfF/ZrnKB6Axdj12UQlWAuHWAfWEVurgDSR6d2KBgRzO1mGJczVLXhBHVKu+W1NZvSRUlfQA2vltIe1lObCiQEVFsC51gQtCC73aohoB367QJu2euVNSPQ8FB/iYXmca7qfi2iCtgZx0XEAtcRDn0w7+cqDMHxdGSoh51m/1vn9k2Bswgm1bkzWaXO50G3aOvRPrMFi04eYf827EwqqoT6miwm8RZKmayi8LZVoc043KlWaU1yMF1OVefH15CRrY1xnL+R6hMh6+04w7O/iZpnQz6suiY1jTf76G9iYOpmApvvpMTAAiiPSK0TJ0gJXj4Hs/zlIrr5n/8Bj3oQCknmmsUAAAAASUVORK5CYII=» style=»vertical-align: middle;» />. Точка покоя неустойчива (неустойчивый фокус, рис.36);

3. Корни кратные:

а) . Точка покоя асимптотически устойчива (устойчивый узел, рис.38, 39);

б) 0″ png;base64,iVBORw0KGgoAAAANSUhEUgAAAGgAAAATBAMAAACO11WQAAAALVBMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAACttl6nAAAADnRSTlMAQoFewKTnMRAg0CJxkY7DLSgAAAFdSURBVCjPY2AgC/D4YBc/cgC7uDiYjDPAKsn6GKtwWWg6iJoXgFWW8xU2Ue5kBrMNQJrrJXZ3+G2AM6dOgLF4HzDwXQDSzG+wa7JDeIrRtQDKYnNgYFkApDleYdfUl4BgM4YIQBh8QE0PwCEBM4aBXRAMGiAh8RzZLyGQ4NoH02QHdCQnWIhZCQwghjC/ZWBolIDrCgPrkgNqeggyPi2BYdISLIGbxsAZGAYPAg4tAyRNZqWPGTpVMPSwp8cZ8AZwBaBqgvqJ+SHjUwYGFQzn2RnUBfAu4IWFBjdYDyj0uBJAkgxpDVBNSAHB/JiB7QUwEqE2cUdBAoIVGE8BYO/qGTBgOM8ugIEJmJCsGqCBBw1yxocMcgIgfQzzHDA1AZ3MmcLA7gFR6iIAEzc7kwx0EcgcAUxNIH9tZGhpACeLUkSK4jaGhyemJkiIOQoG4M5UJWnOWLPHu3cXGKgEAGUFSl2PiR1zAAAAAElFTkSuQmCC» style=»vertical-align: middle;» />. Точка покоя неустойчива (неустойчивый узел, рис.40, 41).

Пример 1. Определить характер точки покоя (0,0) системы

Решение. Составляем характеристическое уравнение

lambda_2=3-sqrt>0″ png;base64,iVBORw0KGgoAAAANSUhEUgAAAS8AAAAXBAMAAACortSfAAAALVBMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAACttl6nAAAADnRSTlMAQRGBpGbAgugg0DGRUU3Z2TAAAAPiSURBVEjH7VbdS5NRGH/ed3v30TZZZUE3Mk3Muoih4IUXMi3NLRhvRmQFY2mJGogYfdCFSKVMLFmgoRAiYiB9yAITMYgFEeWF6EW34nTm1Lm/ofPxfu19T2qw7nou9Ow55/zO7/yej/cA/Ld/badHkXlyBofRRnMBxA9mkHXmipcZo6VygWRqKEKWM8VeYrQi9tz5JbY0J5humwdeGJycWyXezD5Fs0Rr1cAfMTg/0HuXrjG31D18y3Jfhfn2pE4w17Pv6rGLImub8K6e5bePw0KH/pyS5id0zwYLydnEp+j5XFTrn+DvQCicvXZkSehXfoyFWXBzMcsuw20VnaIjEs123oJScgn7NgvJsgEdVAarNghCJ5cEWwKNHD8UZxAgrW7cYsF1h01phvsM2PphMY6rQDnFsQvmHoobZWnfBpmYkdghj5AC8zoeHvfLzj6AVnUjMwCzopPlvwd5O1CANbbXyaG2JsC0Q0YhLztdf0np7M5KMbiB1cSWf1NyooUdatFss7O/9DGjwMaBE2GFBJ9/JDGzrIGVhv1sj7LyMDHChGusYRBr0p4xRJk5MDG1HoIxJSgUjgRk+E2MlWJkA2XEV5ZRYqtg3aThQcLxNJwPiJEFpgp/NjG8hPPhUZWs+lCvLG2Hyj4UB36Z8HRROMLoaEDXlewkxTD9pKzf9TKJmIkSC6SBq2eEM4IQXeXlFefKyzH2PFLcgvlzaracem8g5or0wFB+v1EdvAvBISuTM/sK0d+nrCHMFGLm8QjYLQxiiz5y6fsXyKW5dlSL+aT0VXVOYmJ8Vo41zuzCV5g0pmxK0bALN6sgQp/AE5ql12toWZvI1QOexSWQiN0lN8Lj4jhUhbWh5AuR5G1Y+gE4JgG9ei1X5ZRSlAnUTxagHhR9iNzfolwmK8nstjXUe7AuIsRlXl1EKFSVuB+ZB+CzTyamJv/KGlFMm/zTUZJiJTH4IqXYbaWPJUGgWRoSIeKRZNAkf8bLZXShXUe9B/2vlRIXJX+XdDXax1ARIfKGUI74+MFYNrGQD6cYP9XSmshuFwVuLgEhUttCmtSGa0IH1+5xbupaRQQu4w19LdNeyqtBmnkKpUhD1wbpiQZi3GTlc127sG3NYCT0TlklDbZaCV9vowhzJN/zfOSjNOsxfP+C+qdSt4jZ5yE4XOT2gPItnaudxNuxLJ+MxKDwkkdHTNi8qJl3+NXx8DX0h/x24DPcfJOgh/toeKyM9WqpmtVuwv/UZKPF+8cnk/IR5yPhvZ5WmsmS5fwDvBFTB3jVCa19sf1Xdbv3gtBcLZhJ749mT+bsfV6816Tzr+H8e03+BtfBA04k/tP9AAAAAElFTkSuQmCC» style=»vertical-align: middle;» /> вещественные, разные, положительные. Следовательно, точка покоя — неустойчивый узел.

Связь между типами точек покоя и значениями корней характеристического уравнения (2) можно представить наглядно. Для этого введем обозначения . Тогда характеристическое уравнение запишется в виде .

Рассмотрим плоскость с прямоугольными декартовыми координатами и и отметим на ней области, соответствующие различным типам покоя (рис. 42). Из приведенной выше классификации следует, что условиями устойчивости точки покоя являются . Они выполняются при 0″ png;base64,iVBORw0KGgoAAAANSUhEUgAAADUAAAARBAMAAACP9fljAAAAJ1BMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAB+jSoGAAAADHRSTlMAwEURoSHbgmbwMZHLPgtLAAAAy0lEQVQY02NgwA+YF+CWYzmKKcakAKFjjmBKzd4GMczxTAC6XKQCx1QQzTpZxgEswLUVLufDwHAaRHMX6EAtVPSCySUyMIiBaDMDRpiFKkJQxkEGBhkQXc7AdNIAKhYCkeSCyjEnA+kCmGEhGWBnguSAvmAHiutMhrvCPAkmtwBkHQMD43FUOWaomeUgdXALo8FmMkxkYMiEWIewMEQC7j+g2zkmCgJBzmRUP+goMB1iYGA7AwYnwH53gtnKMaOtASUQuVwR7IhWBgYAYb0rVmdybtQAAAAASUVORK5CYII=» /> и 0″ png;base64,iVBORw0KGgoAAAANSUhEUgAAADAAAAAQCAMAAABncAyDAAAAM1BMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAADbQS4qAAAAEHRSTlMA0GginYExwEIB4FEh8BGxVXXvTAAAAL9JREFUKM+1kdsOAyEIREURvC///7WV3U1bL0nbh/pgonJkhjHmbysGir/U24SY6Pv6IKFDte3eyJf18oC+NbH73xjdbKCy7sLXMftz0TsSBsDJBYj6biBVBBLk9y7IYbDwAhpAMaWimYbmkHMcAZMU8FU9Mq9eHKa8doiCJ7sFYAPQOSonfi1n+5QUbwDuRLquKRIaTRu+cuhqYrJK5SmJYxyryUKatNolwIPpQ3BdQ7KY7qBLmdS4Xf7OZpX9AFDMBpP54cUeAAAAAElFTkSuQmCC» />, т. е. для точек, которые находятся в первой четверти.

Если и комплексные, то точка покоя будет типа фокуса. Этому условию удовлетворяют точки, которые лежат между ветвями параболы и не принадлежат оси .

Точки полуоси , для которых 0″ png;base64,iVBORw0KGgoAAAANSUhEUgAAADUAAAARBAMAAACP9fljAAAAJ1BMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAB+jSoGAAAADHRSTlMAwEURoSHbgmbwMZHLPgtLAAAAy0lEQVQY02NgwA+YF+CWYzmKKcakAKFjjmBKzd4GMczxTAC6XKQCx1QQzTpZxgEswLUVLufDwHAaRHMX6EAtVPSCySUyMIiBaDMDRpiFKkJQxkEGBhkQXc7AdNIAKhYCkeSCyjEnA+kCmGEhGWBnguSAvmAHiutMhrvCPAkmtwBkHQMD43FUOWaomeUgdXALo8FmMkxkYMiEWIewMEQC7j+g2zkmCgJBzmRUP+goMB1iYGA7AwYnwH53gtnKMaOtASUQuVwR7IhWBgYAYb0rVmdybtQAAAAASUVORK5CYII=» />, соответствуют точкам покоя типа центра.

Точки, расположенные вне параболы 4Delta)» png;base64,iVBORw0KGgoAAAANSUhEUgAAAKcAAAAZBAMAAACm+CPaAAAALVBMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAACttl6nAAAADnRSTlMAAb6BKEHnXaEQ0AlxkSizG6IAAAK8SURBVEjHtZVBa9RAFMff7KZmAy0kcYngYdmNpWihYWmwailL6mGpIktR97p0tUXsIUSQpfRQeihWpZYiuPQgYhGhXvoZhOq9B08eBFu79ZTP4HuTpMluWpg9+A5DMvnnN/P+82YG4P+FZDui0vc3RJUz905EpWt3VwWVP2FUUDkwL/8RlC7BxDlf3kUPudnAqOGB43Okd3giyZ7dlCbvUVuZDV83ov7sXEqa5cMdUdtOLM7gl5TychEbxS0Gb/JO1F9Nr2lFpVQ6W2TPx7j79lZaSbisFSZ7wQu7leF0Tj5Bq1YZW/YkLqmDbKrKLIK2Zw6D15Ya9m87z3nGz2Kp7tLH9cbTLiFU7fFeqF4j6E3JD0y9GvW/sa/xCU/G1CkLQVJTJ1NZjbvzwLavj5tXeqFTBYQq87DJTWWPafL7tv3NNAOXlclbUU4lgua8AW6q8RWbt76/GPmQr/OgsfIlgl5ahRovS4msrfidkbjyleWQqjsErarMJVN1GnN0un26sLLNw+FKghoO5P7ymkfo4In2K7mebPlHkBMQdB1ghUzN4G/yMQz97smcrN4Hgi7hHH0nhFbL0JiFLuornj1BpSZOgUzNlLAadyDTPOOEWag3PjtsHh83V0NoxYGVbuh9gma+1/ceQg5TlzvkLUILZTCK6fTzprn3yJOJx00lKB4PL9Qks8X3pG6a7hi00RjmeoGnH7zE8NLpQjGARhGMaY1pOpmqINQE5agr+Wj5KX1bw1hpBtDMQT7eA1oyuUYJWibGCJlKJTUB28X4c1xSoO4xZZGkFh6gBvog7b72zjxzCr5fdn0eZMJLdGvsU5IZF7/lH14MlB10C/Nm0vQ5J5mmghYEGdmiYzDh6FBimzJNZaEUjVbFLxzDE9PxrScaclHwZpjr527cEJO1nX6gOTH1Wn/XuCbmKa7TP6ovmlkrqbjpAAAAAElFTkSuQmCC» style=»vertical-align: middle;» />, соответствуют точкам покоя типа узла.

Область плоскости , где , содержит точки покоя типа седла.

Исключая особые случаи (прохождение через начало координат), замечаем, что седло может перейти в узел устойчивый или неустойчивый (рис.42). Устойчивый узел может перейти либо в седло, либо в устойчивый фокус. Случай равных корней соответствует границе между узлами и фокусами, т.е. параболе .

Пример 2. Исследовать уравнение упругих колебаний с учетом трения и сопротивления среды (при 0″ png;base64,iVBORw0KGgoAAAANSUhEUgAAADEAAAAQBAMAAABNQoq8AAAALVBMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAACttl6nAAAADnRSTlMAAcGe2BFbQSGBMfCxcU2qjNsAAADDSURBVBjTY2AgDYgvxCHB5WyyALtM9wW2HUhcDgs4006A8TGyyprjAlCWiwCjCpDNekkzACLQrA6RYnwkwKgHZK42DVFghkq5CcBlAhi4NjOwPSuGGtMJlmJ/xMCgV8DA9JSB6yXc8kg3IMEKkelTAOo2gMv4Iuypm8DA+DoArgVkGiPQbdpgGdY3DDAXQP3DAPKPiAFjkRMbiqsZ1iWwPweGkY+RafYxEL8IJsHA5jklAeSShQysIHtYEaHD2JbKwAAA/gYrl5lLD9QAAAAASUVORK5CYII=» />)

Решение. Переходим от уравнения (3) к эквивалентной ему системе уравнений