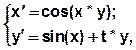Scilab решение дифференциальных уравнений 2 порядка

Дифференциальные уравнения возникают в широком классе задач по описанию управляемых энергетических, промышленных и других процессов и комплексов. В настоящее время наблюдается бурное развитие робототехники, разработка и эксплуатация новых моделей роботов и промышленных манипуляторов, что стимулирует активные исследования по математической и прикладной теории управления, моделированию и конструированию управляемых систем.

Дифференциальные уравнения возникают в широком классе задач по описанию управляемых энергетических, промышленных и других процессов и комплексов. В настоящее время наблюдается бурное развитие робототехники, разработка и эксплуатация новых моделей роботов и промышленных манипуляторов, что стимулирует активные исследования по математической и прикладной теории управления, моделированию и конструированию управляемых систем.

Мы рассмотрим способы исследования сложных механических систем, моделируемых дифференциальными уравнениями. Рассмотрим способы конструирования управления нескольких видов для механической системы с двумя степенями свободы. А также, проведем визуализацию процесса стабилизации движения.

Дифференциальные уравнения n-го порядка

Дифференциальным уравнением n-го порядка называется соотношение вида

Решением дифференциального уравнения является функция ( x(t) ), которая обращает это уравнение в тождество. Дифференциальные уравнения имеют бесконечное множество решений.

Чтобы однозначно определить решение некоторой задачи, необходимо задавать начальные условия. Количество таких условий должно совпадать с порядком уравнения. А решение, найденное для таких условий называется решением задачи Коши.

6.2 Пример решения оду в Scilab

Для решения обыкновенных дифференциальных уравнений (ОДУ) в Scilab используется
функция y = ode([type], y0, t0, t, func).
Разберём, что обозначает каждый из параметров у этой функции.

type — необязательный строковый параметр, с помощью которого можно выбрать метод решения ОДУ. Обычно этот параметр опускается.
t0 — скаляр начальный момент отрезка интегрирования. Обычно ( t0 = 0 ).
y0 — начальные условия. Отметим, что (y0 ) это вектор, размерность которого совпадает с порядком ОДУ. Так, для ОДУ 2-го порядка необходимо задать значения в начальный момент времени для функции и её производной, т.е. использовать запись (y0 = [0.1, 0.3]).
t — вектор, задающий узлы сетки, в которых ищем решение. Как правило, вектор t задается следующим образом t=t0:d:tmax, где (t0) — начальный момент отрезка интегрирования, (d) — шаг дискретизации, (tmax) — конечный момент отрезка интегрирования.
func — пользовательская функция, определяющая правую часть уравнения.
y — вектор решений.

Рассмотрим использование функции ode() на примере решения следующей задачи.

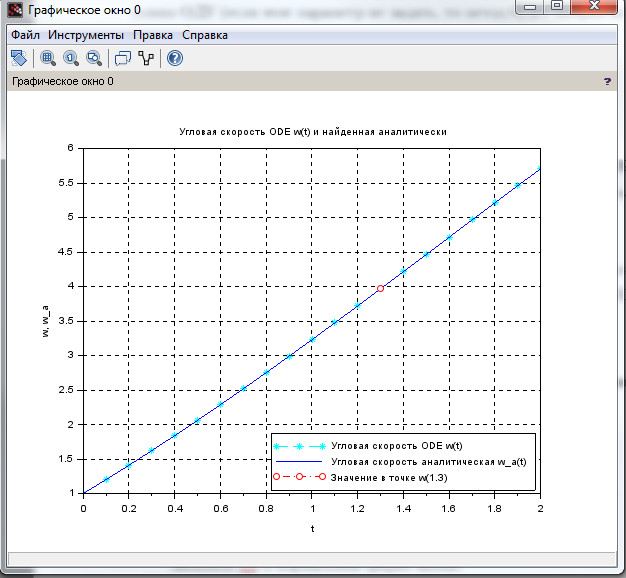
Найти угловую скорость ( omega(t) ) твердого тела вокруг неподвижной оси, если заданы начальная угловая скорость тела ( omega_0=1 ) и угловое ускорение ( varepsilon(t) = 2+0.5sin(t) ). Найти значение ( omega(t) ) в момент времени ( t_1=1.3 ). Построить график функций.

Рисунок 9. Сравнение графиков угловой скорости точки, по функции, найденной аналитическим и численным интегрированием. Красным кружком обозначено значение скорости точки в момент времени t=1.3c.

Угловая скорость точки может быть найдена из дифференциального уравнения

В нашем случае по условию задачи указаны следующие параметры для функции ode():
(t0=0 ) начальный момент времени,
(y0 = 1) начальное условие одно, т.к. порядок уравнения равен 1, это начальная угловая скорость тела ( omega_0=1 )
t=t0:h:tmax — вектор, задающий узлы сетки.

Результат работы программы представлен на рис.9, исходный код на листинге 15.

Отметим, что в данной программе фигурирует пользовательская функция aomega(t), представляющая собой угловую скорость, найденную аналитически с указанным начальным условием.

Функция ( f = 2t — 0,5cos(t) + 1,5 ) единственное решение дифференциального уравнения, удовлетворяющее заданным начальным условиям, то есть, функция (f) решение задачи Коши.

6.3 Cистемы дифференциальных уравнений

Для решения систем ОДУ в Scilab используется та же функция y = ode([type], y0, t0, t, func). Однако важным требованием является запись исследуемой системы в нормальной форме Коши.

Системой дифференциальных уравнений, записанной в нормальной форме Коши называется система, где слева стоят производные фазовых переменных, а справа некоторые функции, т.е. система вида

begin x_1′ = f_1(t,x_1. x_n) \ x_2′ = f_2(t,x_1. x_n) \ . \ x_n’ = f_n(t,x_1. x_n) end

Решением системы ОДУ является вектор x(t), который обращает это уравнение в тождество. Размерность вектора равна количеству уравнений в системе.

Стоит отметить, что дифференциальное уравнение n-ой степени может быть представлено в виде системы из n-уравнений первой степени, что позволяет решать задачу Коши для полученной системы ОДУ.

6.4 Примеры поиска решения систем ОДУ в Scilab

Решение системы ОДУ

Рассмотрим решение задачи Коши для системы уравнений

begin x’ = cos(xy) \ y’ = sin(x+ty) end

на интервале ( [0; 10]) и с начальными условиями (x(0)=0, y(0)=0 ).

Для поиска решения данной задачи, нам необходимо привести исходную систему к нормальному виду Коши. Для этого введём новые переменные ( (z1, z2) ) и сделаем необходимые переобозначения в исходной системе:

Рассмотрим решение задачи Коши для системы уравнений

begin z_1 = x \ z_2 = y end begin z_1′ = cos(z_1 z_2) \ z_2′ = sin(z_1 + t z_2) end

Код программы, реализующей поиск решения системы дифференциальных уравнений представлен на листинге 16. Обратите внимание, как происходит обращение к компонентам вектора решения ( z(t) ).

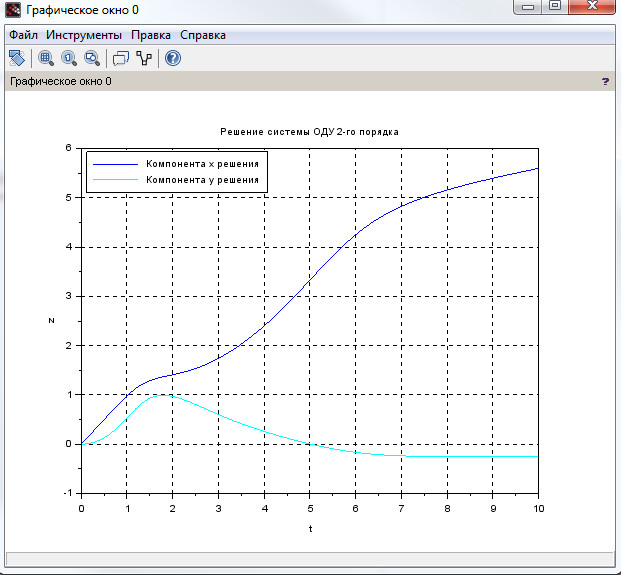
Для наглядной реализации сформировано графическое решение на рис. 10.

Рисунок 10. Графическое решение задачи Коши с помощью функции ode().

Решение системы ОДУ в матричной форме

Рассмотрим решение задачи Коши для системы уравнений, заданных в матричном виде

на интервале ( [0; 10] ) и начальными условиями ( y_1(0)=1, y_2(0)=0 ).

Код программы, реализующей поиск решения системы дифференциальных уравнений представлен на листинге 17. Обратите внимание, как происходит обращение к компонентам вектора решения (y(t)).

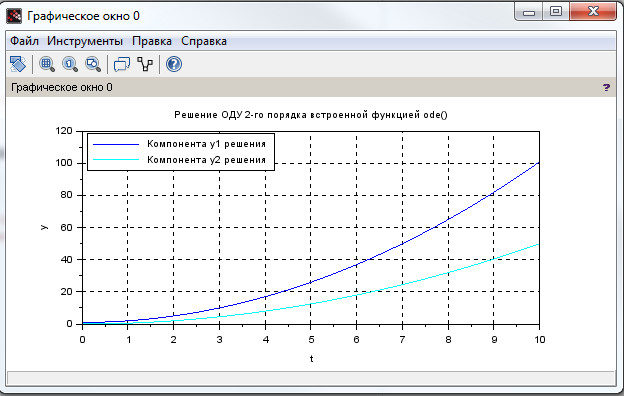
Для наглядной реализации сформировано графическое решение на рис. 11.

Рисунок 11. Графическое решение задачи Коши с помощью функции ode().

Решение ДУ 2-го порядка путём сведения к системе уравнений

Продолжим знакомиться с возможностями функции ode() на примере решения задачи механики на второй закон Ньютона.

Груз находится на пружине жёсткости ( c=12 ) H/м, масса груза ( m=68.7 ) кг. Определить закон движения груза, если на него действует сила ( F=100.5sin(2t) + ) H.

По 2-му закону Ньютона, движение груза описывается с помощью дифференциального уравнения 2-й степени, которое имеет вид:

и начальными условиями ( x(0)= 0, ; dot(0)= 0 ).

Как известно, ОДУ второго порядка сводится к системе в нормальной форме Коши, состоящей из двух уравнений первой степени. Введём новые переменные ( (z_1, z_2) ) и сделаем необходимые переобозначения в исходной системе:

begin z_1 = x \ z_2 = dot end begin dot_1 = z_2 \ dot_2 = (-cz_1 + F(t)) end

Код программы, реализующей поиск решения системы дифференциальных уравнений представлен на листинге 18. Обратите внимание, как происходит обращение к компонентам вектора решения ( y(t) ).

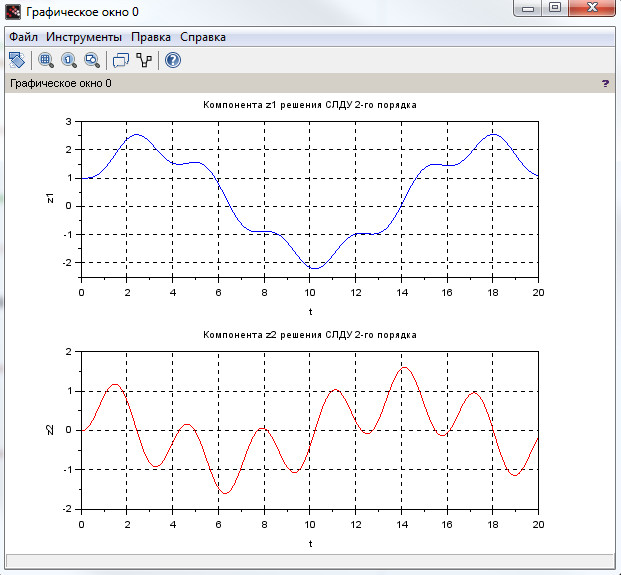
Для наглядной реализации сформировано графическое решение на рис. 12. Компонента ( z_1 ) представляет собой координату груза, а компонента ( z_2 ) — скорость груза.

Рисунок 12. Графики движения груза на пружине для компонент ( z_1 и z_2 ) соответственно.

Scilab решение дифференциальных уравнений 2 порядка

Для решения ОДУ и системы ОДУ 1-го порядка в Scilab предусмотрена функция ode , имеющая форматы:

[y]=ode(y0,t0,t,f),

[y,w,iw]=ode(type,y0,t0,f,adams,stiff,rk,rkf,fix,rtol,adol,jac,w,iw),

которые содержат обязательные и необязательные параметры.

Первый формат функцииode содержит только обязательные параметры, к которым относятся:

y 0 – вектор начальных условий;

t 0 – начальная точка интервала интегрирования;

t – координаты узлов сетки, в которых происходит поиск решения;

f– имя внешней функция, определяющей правую часть уравнения

или системы уравнений;

y – вектор решений (выходной параметр).

Второй формат функции odeсодержит ряд необязательных параметров. Эти параметры позволяют выбрать метод решения или тип решаемой задачи:

type– строка, указывающая тип используемой программы решения, может принимать значения: » adams «, » stiff «, » rk «, » rkf «, » fix «, » discrete «или » root «;

adams– применяют при решении дифференциальных уравнений или систем методом прогноза и коррекции Адамса;

stiff– указывают при решении жестких задач;

rk– используют при решении дифференциальных уравнений или систем методом Рунге-Кутты четвертого порядка;

rkf– указывают при выборе пятиэтапного метода Рунге-Кутты четвертого порядка;

fix– тот же метод Рунге-Кутты, но с фиксированным шагом;

rtol, atoll– относительная и абсолютная погрешности вычислений, соответственно, по умолчанию rtol =0.00001, atol =0.0000001 (при использовании параметров rkfи fix– rtol =0.001, atol =0.0001);

jac– матрица, представляющая собой якобиан правой части жесткой системы дифференциальных уравнений и заданная в виде внешней функции вида j = jak ( t , y );

w, iw– векторы, предназначенные для сохранения информации о параметрах интегрирования, которые применяют для того, чтобы последующие вычисления выполнялись с теми же параметрами.

Описание этого формата достаточно подробно рассмотрено в справочной системе Scilab, где и приведены примеры его использования для различных типов ОДУ [13].

Остановимся на использовании первого формата функции ode, для чего рассмотрим решение следующего примера: найти решение ОДУ y ‘=- sin ( x * y ) на отрезке [0;5]cшагом 0.5 при начальных условиях y (0)=1.5.

Решение ОДУ, полученное с применением функции ode и график полученного решения, представлены на рис.2.5.2-1.

—> // Решение ОДУy’=-sin(x*y) —> y0 = 1.5; t0 = 0; t = 0:0.5:5; // Начальные условия —> // Загрузка и выполнение сценарияРИС2521 —> exec(‘РИС2521.sce’, 0); ans = 0. 1.5 0.5 1.3302706 1. 0.9566472 1.5 0.5574285 2. 0.2477507 2.5 0.0822207 3. 0.0208664 3.5 0.0041103 4. 0.0006303 4.5 0.0000753 5. 0.000007

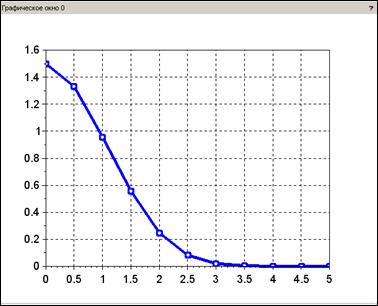Рис. 2.5.2-1. Решение ОДУ с использованием функции ode

Для решения системы обыкновенных дифференциальных уравнений в Scilab предназначена функция:

y=ode(x0,t0,t,sys),

где х0 – вектор начальных условий ОДУ;

t 0 – начальная точка интегрирования;

t– вектор значений независимой переменной;

sys– имя функции, в которой исходя из вектора значенийtвычисляется матрица решенийy;

y– матрица решений (выходной параметр), первый столбец которой

y (1)– значение функции y ( x ), а второй — y (2 )–значение производной y ‘( x ).

Решение системы ОДУ формируется в матрице y, и выводится на экран в виде таблицы

В качестве примера рассмотрим решение системы ОДУ:

c начальными условиями x(0)=0, y (0)=0 на отрезке [ 0;10] и шагом 1 .

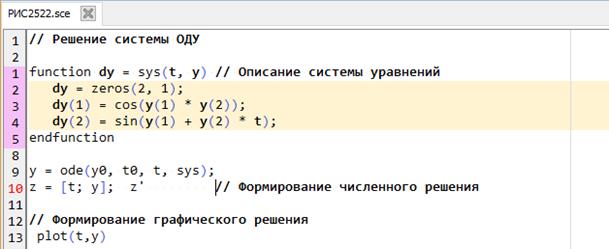
Решение системы ОДУ в Scilab начинается с создания функции sys, описывающей систему (рис.2.5.2-2). После того, как заданы начальные условия ОДУ, производится обращение в функции ode, в результате которого формируется матрица решения y. Решение системы выводится в виде таблицы и графика. (Шапка таблицы и легенда для графика!)

—> // Решение системы ОДУ —> // Загрузка сценария РИС2522 и его выполнение —>clear —> // Начальные условия —>x0 = [0; 0]; t0 = 0; t = 0:1:10; —> —> exec(‘РИС2522.sce’, 0); ans = 0. 0. 0. 1. 0.9802401 0.533358 2. 1.4096497 0.9693978 3. 1.7429464 0.6024417 4. 2.4027415 0.2586293 5. 3.3312751 0.005761 6. 4.2504071 -0.1650347 7. 4.826261 -0.2358589 8. 5.1581587 -0.2515654 9. 5.3963437 -0.2509281 10. 5.5981318 -0.2461951

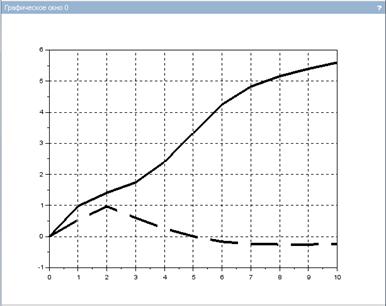Рис.2.5.2-2. Решение системы ОДУ

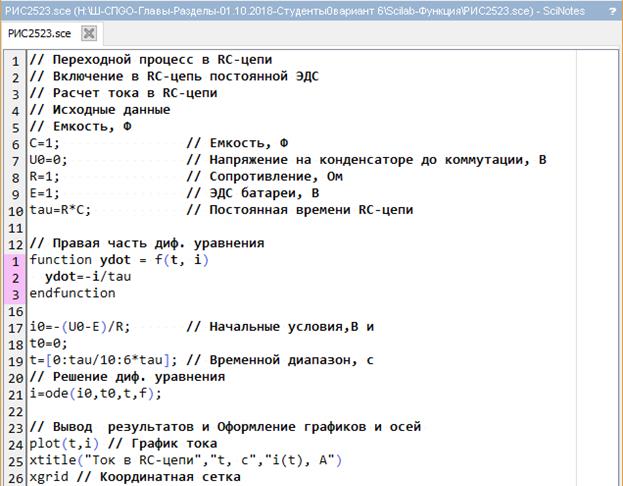
Рассмотрим задачу построения временной зависимости тока i ( t ) в RC-цепи.

Построить временную зависимость тока i ( t ) в неразветвленной RC-цепи (рис. 3.3-4), если цепь включается на постоянное напряжение при нулевых начальных условиях.

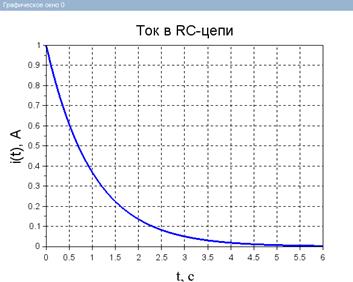
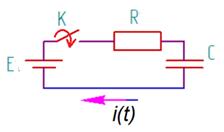Неразветвленная RC -цепь Дано: E=1 В – ЭДС источника; R=1 Ом – сопротивление; С=1 Ф – емкость; t=[0, 6τ] c – временной интервал.

Рис.2.5.2-3. Построить временную зависимость тока i ( t ) в RC-цепи

Основы работы в SciLab. На примере экзаменационных вопросов по КСВЭ

Завтра мне сдавать экзамен по такому предмету как КСВЭ(Компьютерный сервис вычислительного эксперимента). А лучший способ подготовки — это написание статьи. Я рассмотрю часть вопросов к экзамену, которые связаны с SciLab.
Статья больше подходит для студентов, использующих scilab для проверки решения, для или для сдачи экзамена по дисциплине КСВЭ. Для более подробного изучения надо читать литературу, указанную в конце статьи

Основные термины
Scilab (читается Сайлэб) — пакет прикладных математических программ, предоставляющий мощное открытое окружение для инженерных (технических) и научных расчётов.
CeCILL (от «CEA CNRS INRIA Logiciel Libre») — это лицензия на свободное программное обеспечение, адаптированная к интернациональному законодательству и законодательству Франции, подобная GNU General Public License и сохраняющая совместимость с ним.
Система m линейных алгебраических уравнений с n неизвестными (или, линейная система, также употребляется аббревиатура СЛА́У) в линейной алгебре — это система уравнений вида

Обыкнове́нные дифференциа́льные уравне́ния (ОДУ) — это дифференциальное уравнение вида

где — неизвестная функция (возможно, вектор-функция, тогда, как правило, тоже вектор-функция со значениями в пространстве той же размерности; в этом случае говорят о системе дифференциальных уравнений), зависящая от независимой переменной, штрих означает дифференцирование по. Число (порядок старшей производной, входящей в данное уравнение) называется порядком дифференциального уравнения (1)

1. Система компьютерной математики SciLab: История разработки. Возможности и ключевые особенности. Достоинства и недостатки.

История
С 1994 года распространяется вместе с исходным кодом через Интернет. В 2003 году для поддержки Scilab был создан консорциум Scilab Consortium. Сейчас в него входят 25 участников, в том числе Mandriva, INRIA и ENPC (Франция).

Scilab содержит сотни математических функций, и есть возможность добавления новых, написанных на различных языках (C, C++, Fortran и т. д.). Также имеются разнообразные структуры данных (списки, полиномы, рациональные функции, линейные системы), интерпретатор и язык высокого уровня.
Scilab был спроектирован как открытая система, и пользователи могут добавлять в него свои типы данных и операции путём перегрузки.
В системе доступно множество инструментов:
2D и 3D графики, анимация
Линейная алгебра, разреженные матрицы (sparse matrices)
Полиномиальные и рациональные функции
Интерполяция, аппроксимация
Симуляция: решение ОДУ и ДУ
Scicos: гибрид системы моделирования динамических систем и симуляции
Дифференциальные и не дифференциальные оптимизации
Обработка сигналов
Параллельная работа
Статистика
Работа с компьютерной алгеброй
Интерфейс к Fortran, Tcl/Tk, C, C++, Java, LabVIEW
Scilab имеет схожий с MATLAB язык программирования. В состав пакета входит утилита, позволяющая конвертировать документы Matlab в Scilab.
Scilab позволяет работать с элементарными и большим числом специальных функций (Бесселя, Неймана, интегральные функции), имеет мощные средства работы с матрицами, полиномами (в том числе и символьно), производить численные вычисления (например, численное интегрирование) и решение задач линейной алгебры, оптимизации и симуляции, мощные статистические функции, а также средство для построения и работы с графиками.
Для численных расчётов используются библиотеки Lapack, LINPACK, ODEPACK, Atlas и другие.
В состав пакета также входит Scicos — инструмент для редактирования блочных диаграмм и симуляции (аналог simulink в пакете MATLAB). Имеется возможность совместной работы Scilab с программой LabVIEW.

Ключевые особенности
Отличия от некоторых коммерческих программ:
Бесплатность.
Свободность (с версии 5.0).
Маленький размер — дистрибутив 4 версии занимал менее 20 МБ против более чем двухгигабайтного пакета MATLAB. Инсталлятор 5 версии (5.4.0) увеличился в объёме до 108 МБ.
Возможность запуска в консоли без использования графического интерфейса, в том числе в версии под Windows (в UNIX и Windows версиях MatLab-а эта возможность присутствует тоже). Это позволяет производить автоматизированные вычисления, есть пакетный режим.

Достоинства и недостатки
Поиски достоинства и недостатков на просторе интернета ни чего не дали. Так что расскажу о том, что я заметил сам.
Если говорить о достоинствах, тут самым основным для меня является бесплатность данного пакета, по сравнению с той же Mathematic, когда для выполнения лабораторных работы приходилось искать серийник или crack. Далее — это кросплатформеность, т.к. я больше предпочитаю использовать Gentoo, чем Windows. В принципе большенство достоинств описано в пункте Ключевые особенности.
Из недостатков я вижу только 2: Это нет такой визуализации программирования как в Mathematic, а так же система использует прежде всего численные подходы, для вычисления, что может сказаться на точности.

2. Основы работы в SciLab. Пользовательские и системные переменные. Математические выражения. Коментарии

При написании данной статьи я использую версию scilab-5.3.3 под windows.
SciLab 5.3.3
Операционные системы: Windows, Linux, MacOS
Пользовательские и системные переменные
Год/Дата Выпуска: 2011
Версия: 5.3.3
Разработчик: Free Open Source Software for Numerical Computation
Сайт разработчика: www.scilab.org
Разрядность: 32bit+64bit
Лицензия: CeCILL
По характеристикам данных не нашёл, но могу сказать, что данный пакет грузится без глюков на моём ноутбуке
Процессор: Intel Celeron Dual-Core T3300 2.0 ГГц
Оперативная память 2Гб DDR3
Видеоадаптер Intel GMA4500M

Прежде чем перейти дальше, рассмотрим сам интерфейс. При запуске открывается командное окно.

Есть 2 варианта работы: 1 — это работа в том же командном окне, 2 — открыть SciNotes(что-то вроде блокнота с подсветкой) где можно написать код, который позднее запустить, результат выполнения появится в командном окне.

Для примера я рассмотрю вывод Hellow world.

Командная строка. Используем функцию вывода на дисплей disp()

При работе в SciNotes вы получите что то похожее

для выполнения кода, надо или нажать на стрелочку в право 🙂 (как во многих средах разработки)
или Выполнение->… без отображение команд
в принципе можно использовать и другие методы выполнения, и не использовать вывод на экран
Результатом выполнения будет:

т.к. можно сказать что интерфейс изучен, далее я буду приводить просто код и результат выполнения

SciLab чувствителен к реестру, т.е. А и а — разные переменные переменные.

a=1,A=3
//Каждая операция начинается с новой строки или через запятую
//коментарии можно оставлять после двух символоф слэш
b=3
c=a+b
disp©

Основные операции:
+ сложение
— вычитание
* умножение
/ деление справа, т.е. x/y = xy^(-1)
деление слева, т.е. xy = x^(-1)y
^ возведение в степень, т.е. x^y
** возведение в степень (эквивалентно ^)
’ эрмитово сопряжение (комплексное сопряжение и транспонирование)

3. Основы работы в SciLab. Функции и их типы. Способы объявления пользовательских функций. Использование функций. Файлы-сценарии и их применение для хранения функций.

Элементарные математические функции.

acos acosd acosh acoshm acosm acot acotd acoth
acsc acscd acsch asec asecd asech asin asind
asinh asinhm asinm atan atand atanh atanhm atanm
cos cosd cosh coshm cosm cotd cotg coth
cothm csc cscd csch sec secd sech sin
sinc sind sinh sinhm sinm tan tand tanh
tanhm tanm
exp expm log log10 log1p log2 logm max
maxi min mini modulo pmodulo sign signm sqrt
sqrtm

y = int8(x) 8-битовое число со знаком [-2^7; (2^7)-1] = [-128; 127]
y = uint8(x) 8-битовое число без знака [0; (2^8)-1] = [0; 255]
y = int16(x) 16-битовое число со знаком [-2^15; (2^15)-1] = [-32768; 32767]
y = uint16(x) 16-битовое число без знака [0; (2^16)-1] = [0; 65535]
y = int32(x) 32-битовое число со знаком [-2^31; (2^31)-1] = [-2147483648; 2147483647]
y = uint32(x) 32-битовое число без знака [0; (2^32)-1] = [0; 4294967295]

iconvert преобразование к целочисленному представлению
inttype определение типа целого числа

простейший способ вызова пользовательской функции:

пример пользовательской фунции:

function y = myfunction ( x )
y = 2 * x
endfunction

Сохраняем её. Далее приведён пример вызова данной функции

4. Определение одномерный и многомерных массивов. Основные действия над массивами.

Пример, как задаётся одномерный массив:

квадратные скобки ”[” и ”]” обозначают начало и конец перечисления
элементов матрицы,
запятой ”,” отделяются элементы матрицы, находящиеся в одной строке,
точка с запятой ”;” разделяет строки матрицы.

size определить размер матрицы
matrix изменить размер матрицы
resize_matrix создать новую матрицу заданного размера и скопировать
в нее элементы из исходной матрицы

Операции над матрицами:
Обращение к элементам матрицы
i = 1; 2, а j = 3; 4
для этого возьмём уже готовую матрицу

—>A = testmatrix (» hilb «, 5)
A =
25. — 300. 1050. — 1400. 630.
— 300. 4800. — 18900. 26880. — 12600.
1050. — 18900. 79380. — 117600. 56700.
— 1400. 26880. — 117600. 179200. — 88200.
630. — 12600. 56700. — 88200. 44100.
—>A(1: 2, 3: 4)
ans =
1050. — 1400.
— 18900. 26880

A матрица целиком
A(. ) матрица целиком
A(i:j,k) элементы матрицы в k-ом столбце с i-ой по j-ую строку
A(i,j:k) элементы матрицы в i-ой строке с j-ого по k-ый столбец
A(i,:) i-ая строка матрицы
A(:,j) j-ый столбец матрицы

Генерация единичной матрицы

Операции над матрицами
+ сложение .+ поэлементное сложение
— вычитание .- поэлементное вычитание
* умножение .* поэлементное умножение
/ деление справа ./ поэлементное деление справа
деление слева . поэлементное деление слева
^ или * возведение в степень :^ поэлементное возведение в степень
’ эрмитово сопряжение (комплексное сопряжение и транспонирование)
.’ транспонирование без сопряжения

пример умножения числа на еденичную матрицу 2 на 2

5. Определение одномерный и многомерных массивов. Специальные матричные функции

функции работы с матрицами
chol разложение Холесского
companion сопровождающая матрица
cond число обусловленности
det определитель матрицы
inv обратная матрица
linsolve решение систем линейных уравнений
lsq метод наименьших квадратов
lu LU-разложение с выбором опорного элемента
qr QR-разложение
rcond обратное число обусловленности
spec собственные значения и векторы
svd разложение по сингулярным числам матрицы
testmatrix генерация специальных матриц (Гильберта, Франка и др.)
trace след матрицы

6. Определение одномерный и многомерных массивов. Решение СЛАУ. Символьные массивы и операции над ними

Текст файла–сценария с решением задачи по формулам Крамера

—>A=[2 1 -5 1;1 -3 0 -6;0 2 -1 2;1 4 -7 6];//Матрица коэффициентов
—>b=[8;9;-5;0]; //Вектор свободных коэффициентов
—>//Первая вспомогательная матрица
—>A1=A;A1(:,1)=b;
—>//Вторая вспомогательная матрица
—>A2=A;A2(:,2)=b;
—>//Третья вспомогательная матрица
—>A3=A;A3(:,3)=b;
—>//Четвертая вспомогательная матрица
—>A4=A;A4(:,4)=b;
—>//Главный определитель отличен от нуля
—>D=det(A);
—>//Определители вспомогательных матриц
—>d(1)=det(A1);
—>d(2)=det(A2);
—>d(3)=det(A3);
—>d(4)=det(A4);
—>//Вектор неизвестных
—>x=d/D
x =
3.
— 4.
— 1.
1.
—>//Проверка
—>P=A*x-b
P =
0.
0.
— 8.882D-16
2.665D-15

—>A=[2 -1 1;3 2 -5;1 3 -2];
—>b=[0;1;4];
—>//Приведение расширенной матрицы к треугольному виду
—>C=rref([A b]);
—>//Выделение последнего столбца из матрицы,
—>//x — решение системы
—>x=C(1:3,4:4)
x =
0.4642857
1.6785714
0.75
—>A*x //Проверка
ans =
— 5.551D-16
1.
4.

7. Численное интегрирование. Подходы к интегрированию. Интегрирование функций заданных пользователем

Численное интегрирование (историческое название: (численная) квадратура) — вычисление значения определённого интеграла (как правило, приближённое). Под численным интегрированием понимают набор численных методов отыскания значения определённого интеграла.
Интегрирование по методу трапеций
проинтегрируем функцию, корень из 2*x-1 на отрезке от 1 до 10 с разбиением в 1 шаг

—>x=1:10
x =
1. 2. 3. 4. 5. 6. 7. 8. 9. 10.
—>y=sqrt(2*x-1)
y =
column 1 to 6
1. 1.7320508 2.236068 2.6457513 3. 3.3166248
column 7 to 10
3.6055513 3.8729833 4.1231056 4.3588989
—>inttrap(x,y)
ans =
27.211585

Квадратурные формулы Ньютона Котеса

8.Численное дифференцирование. Подходы к дифференцированию.

Численное дифференцирование — совокупность методов вычисления значения производной дискретно заданной функции.
В основе численного дифференцирования лежит аппроксимация функции, от которой берется производная, интерполяционным многочленом. Все основные формулы численного дифференцирования могут быть получены при помощи первого интерполяционного многочлена Ньютона (формулы Ньютона для начала таблицы).
в точке

9. Решение ОДУ средствами SciLab. Функции применяемые для решение ОДУ. Решение краевых задач.

Существует 4 способа для решения ОДУ:
1. С помощью команды ode, которая является солвером для решения обыкновенного
дифференциального уравнения.
2. С помощью команды odedc, которая вычисляет решение смешанной дискретно-
непрерывной системы.
3. Команда dassl, которая дает решение неявно выраженного дифференциального уравнения.
4. С помощью команды impl, которая дает решение неявно выраженного линейного
дифференциального уравнения.

—>y0=1;
—>t0=1;
—>t=1:0.01:1.5;
—>deff(«[ydot]=f(t,y)»,«ydot=y^(1/3)*t»)
—>y=ode(y0,t0,t,f);
—>y_exact=((t^2+2)/3)^(1.5);// это функция точного решения для сравнения
—>my_er=y-y_exact;
—>plot(t,y-y_exact) // это график ошибки вычисления от аргумента t

результатом является такой график

за одно можно увидеть Графическое окно. Построение графиков будет подробно рассмотрено далее.

10. Построение двухмерных графиков в системе SciLab. Основные функции и типы графиков.

Функция plot
рассмотрим пример:

Функция plot2d
Рассмотрим функцию опять на примере:

как мы можем увидеть, у этой функции намного больше функционала.
фунции передаются сразу массивом, так же можно указать цвет линий и отрезок.

Функция polarplot
Служит для построения графика в полярных координатах

получается ромашка

параметры похожи как и в случае с plot2d

11. Построение трёхмерных графиков в системе SciLab. Основные функции и типы графиков.

Существует 4 способа построение графика:
Способ 1.
С помощью команды plot3d. Команда создает 3D график по точкам, заданным матрицами
x, y и z.
Способ 2.
С помощью команды plot3d1. Команда создает 3D график по точкам, заданным
матрицами x, y и z с помощью уровней цвета. Вещь в общем избыточная: величина
координаты z дополнительно еще и покрашена, в зависимости от принимаемого значения
z.
Способ 3.
С помощью команды fplot3d. Это аналог команды fplot3d, но изображаемая поверхность
задана с помощью внешней функции.
Способ 4.
С помощью команды fplot3d1. Это аналог команды plot3d1, но изображаемая поверхность
задана с помощью внешней функции.
Синтаксис этих команд смотри с помощью help.

забыл указать, что в графическом окне есть возможность экспорта данных, т.е. сохранить картинку

Результат такой же как в примере 1

результат такой же, как в примере 2

12. Задача полиномов в SciLab. Символьные операции с полиномами. Решение алгебраический уравнений. Сравнение функций fsolve и roots.

Рассмотрим на примере решения уравнения 2x^4-8x^3+8x^2-1=0

Для решения трансцендентных уравнений в применяют функцию Scilab fsolve(x0,f)
задача

Надеюсь данная статья послужит толчком, для дальнейшего изучения SciLab или решения своих задач/лабараторных

🎥 Видео