Савченко решение задач с помощью уравнений

Презентация была опубликована 6 лет назад пользователемЮрий Гольский

Похожие презентации

Видео:Урок 14 Решение задач с помощью уравнений (5 класс)Скачать

Презентация на тему: » Решение задач с помощью уравнений Методическая разработка Савченко Е.М. МОУ гимназия 1, г. Полярные Зори.» — Транскрипт:

1 Решение задач с помощью уравнений Методическая разработка Савченко Е.М. МОУ гимназия 1, г. Полярные Зори

5 -3x + 8 = 3x – 4 – + – 0x = –12 Нет корней. Нет корней.

6 -6x + 7 = 6x + 7 – + – 0x = 0 x Q

7 0 x = 0 x Q 0 x = 4 Нет корней

8 1 ч 15 мин 1 ч 30 мин

9 1 ч 15 мин 1 ч 30 мин x км/ч 22+x 22-x 1 (22+x) 1 (22-x) =

10 2 ч 2,5 км/ч на 25% меньше 2 ч

11 2,5 км/ч на 25% меньше 2 ч x +2,5 2,5 км/ч x 2(x+2,5) x (x- 2,5 ) 2(x-2,5)

12 2 км на 12 км/ч быстрее t встр=5 мин

13 на 12 км/ч быстрее t встр=5 мин X км/ч (X+12)км/ч 2 км

14 на 50% больше 256 км t встр =8 ч

15 на 50% больше 256 км t встр =8 ч Xкм/ч 1,5x км/ч

Видео:Решение задач с помощью уравнений. Видеоурок 29. Математика 6 классСкачать

Решение задач с помощью уравнений

В презентации рассмотрены два способа решения задач с помощью уравнений: составление схемы и таблицы. Дан алгоритм решения задач с помощью уравнений.

Просмотр содержимого документа
«Решение задач с помощью уравнений»

Шаблон для создания презентаций к урокам математики. Савченко Е.М.

• Попробуйте сформулировать цель урока.

2. Вы уже встречались с таким способом

3. Как вы думаете, что нужно уметь, чтобы

хорошо решать задачи с помощью

Шаблон для создания презентаций к урокам математики. Савченко Е.М.

Шаблон для создания презентаций к урокам математики. Савченко Е.М.

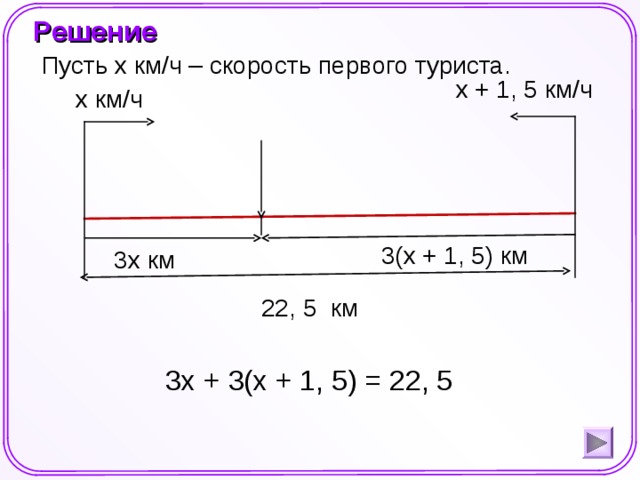
Два туриста вышли одновременно навстречу друг другу из двух пунктов, расстояние между которыми 22, 5 км, и встретились через 3 часа. С какой скоростью шёл каждый из них, если скорость одного на 1, 5 км/ч больше скорости другого?

Шаблон для создания презентаций к урокам математики. Савченко Е.М.

Пусть x км/ч – скорость первого туриста.

Шаблон для создания презентаций к урокам математики. Савченко Е.М.

3x + 3(x + 1, 5) = 22, 5

3x + 3(x + 1, 5) = 22, 5

3x + 3x + 3*1, 5 = 22, 5

Шаблон для создания презентаций к урокам математики. Савченко Е.М.

3 км/ч – скорость первого туриста.

3 + 1, 5 = 4, 5 км/ч – скорость второго туриста.

3x + 3(x + 1, 5) = 22, 5

Шаблон для создания презентаций к урокам математики. Савченко Е.М.

Виктор выходит из дома и идёт в школу со скоростью 60 м/мин. Через 8 минут вслед за ним из этого же дома выходит Иван и идёт той же дорогой со скоростью 100 м/мин. В школу они приходят одновременно. Чему равно расстояние от дома до школы?

Шаблон для создания презентаций к урокам математики. Савченко Е.М.

Шаблон для создания презентаций к урокам математики. Савченко Е.М.

Алгоритм решения задач алгебраическим способом

1) обозначают некоторое неизвестное число буквой х;

2) используя условие задачи, составляют уравнение;

3) решают это уравнение;

4) истолковывают полученный результат в соответствии с условием задачи.

Шаблон для создания презентаций к урокам математики. Савченко Е.М.

Шаблон для создания презентаций к урокам математики. Савченко Е.М.

П. 7.6, № 788 (б), 789 (б)

Шаблон для создания презентаций к урокам математики. Савченко Е.М.

• Что изучали на уроке? Назовите тему.
• Что было самым важным на уроке?
• С какими заданиями ты справлялся сам?
• Что осталось неясным?
• Что получилось лучше всего?
• Что нужно повторить?

Шаблон для создания презентаций к урокам математики. Савченко Е.М.

Шаблон для создания презентаций к урокам математики. Савченко Е.М.

источник шаблона: сайт http://pedsovet.su

Савченко Елена Михайловна,

учитель математики высшей квалификационной категории.

Муниципальное общеобразовательное учреждение гимназия №1,

г. Полярные Зори, Мурманская обл.

Шаблон для создания презентаций к урокам математики. Савченко Е.М.

Видео:Математика 6 класс (Урок№51 - Решение задач с помощью уравнений. Часть 1.)Скачать

Задачи, решаемые с помощью уравнения: примеры, объяснение. Задачи по алгебре

Рано или поздно любому школьнику на уроках алгебры встречаются задачи, решаемые с помощью уравнения. Поначалу появление букв вместо привычных цифр и действия с ними ставят в тупик даже самых одарённых, но если разобраться, всё далеко не так сложно, как кажется на первый взгляд.

Видео:Решение задач с помощью уравнений.Скачать

Алгоритм решения

Перед тем как перейти к конкретным примерам, необходимо понять алгоритм решения задач с помощью уравнений. В любом уравнении есть неизвестное, чаще всего обозначаемое буквой Х. Также и в каждой задаче есть то, что необходимо найти, то же самое неизвестное. Именно его и нужно обозначать как Х. А потом, следуя условию задачи, прибавлять, отнимать, умножать и делить – совершать любые необходимые действия.

После нахождения неизвестного обязательно выполнение проверки, чтобы быть уверенными, что задача решена правильно. Стоит заметить, что дети уже в начальной школе начинают решение задач с помощью уравнений. Примеры этому — те задачи, которые нужно решать отрезками, являющимися полнейшими аналогами буквенных неизвестных.

Видео:Решение задач с помощью уравнений. Алгебра, 7 классСкачать

Основа основ — задача про корзины

Итак, попробуем же на практике применить решение задач с помощью уравнений, объяснение алгоритма которых было дано чуть выше.

Дана задача: Собрали некоторое количество корзин с яблоками. Сначала 3 корзины продали, потом дособирали ещё 8 корзин. В итоге получилось 12 корзин. Сколько корзин яблок собрали первоначально?

Начнём решение задачи с того, что обозначим неизвестное — то есть первоначальное количество корзин – буквой Х. Теперь начинаем составлять уравнение: Х (первоначальное количество) – 3 (проданные корзины) + 8 (те, которые собрали позже) = 12 (итоговое число корзин), то есть Х — 3 + 8 = 12. Решив простое уравнение, получим, что Х = 7. Обязательно выполняем проверку, то есть подставляем найденное число в равенство: 7 — 3 + 8 действительно равно 12, то есть задача решена верно.

Видео:Решение задач с помощью уравнений. Алгебра 7 классСкачать

Закрепление: концертные залы

Дана следующая задача: В двух концертных залах 450 мест. Известно, что в одном зале мест в 4 раза больше, чем в другом. Нужно узнать, сколько мест в каждом зале.

Для того чтобы решать подобные задачи по алгебре, снова нужно применить уравнение. Мы знаем, что сумма двух чисел, одно из которых в 4 раза больше другого, равна 450. Пусть число мест в меньшем зале, неизвестное, будет равно Х, тогда число мест в большем зале – 4 * Х = 4Х. Следовательно, 450 = Х + 4Х = 5Х. А дальше нужно решить стандартное уравнение 450 = 5Х, где Х = 450 / 5 = 90, то есть в меньшем зале 90 мест, значит в большем – 90 * 4 = 360. Чтобы убедиться, что задача решена правильно, можно проверить неравенство: 360 + 90 = 450, то есть ответ верный.

Видео:АЛГЕБРА 7 класс : Решение задач с помощью уравнений | ВидеоурокСкачать

Классика: полки с книгами

Но задачи, решаемые с помощью уравнения, могут быть и посложнее. Например, есть три полки с книгами. На первой полке книг на 8 больше, чем на второй, а на третьей — в 3 раза больше, чем на второй, причём количество книг на первой и третьей полках равное. Сколько книг на каждой полке?

Понятно, что отталкиваться здесь нужно от второй полки, которая встречается в обоих условиях. Если мы обозначаем количество книг на ней за Х, то тогда на первой полке Х + 8 книг, а на третьей — Х * 3 книг, при этом Х + 8 = 3Х. Решив уравнение, получаем Х = 4. Выполняем проверку, подставляя неизвестное в равенство: 4 + 8 действительно равно 3 * 4, то есть задача решена правильно.

Видео:Алгоритм решения задач с помощью систем уравнений. Практическая часть. 9 класс.Скачать

Практикуемся дальше: бобры

Как видите, решение задач с помощью уравнения гораздо легче, чем кажется на первый взгляд. Закрепим навыки работы с уравнениями ещё одной задачей. Первый бобр сгрыз за день какое-то количество деревьев. Второй бобр сгрыз в 6 раз больше. Третий бобр сгрыз в 2 раза больше деревьев, чем первый, но в 3 раза меньше, чем второй. Сколько деревьев сгрыз каждый бобр?

Задача не такая запутанная, какой кажется на первый взгляд. Для начала найдём неизвестное – в этой задаче это количество деревьев, сгрызенных первым бобром. Следовательно, второй бобр уничтожил 6 * Х деревьев, а третий – 2 * Х, причём это число в 3 раза меньше 6 * Х. Составляем уравнение: 6Х = 3 * 2Х. Решив его, получаем, что первый бобр погрыз всего одно дерево, тогда второй – 6, а третий – 2. Подставив числа в уравнение, понимаем, что задача решена верно.

Видео:Решение задач с помощью уравнений | Алгебра 7 класс #19 | ИнфоурокСкачать

Соотносим уравнения и условия

Если вам скажут: «К каждой задаче подберите соответствующее уравнение», — не пугайтесь – это целиком и полностью реально.

Даны следующие уравнения:

Условия задач следующие:

1. У мальчика было 6 яблок, а у девочки в два раза меньше, сколько было яблок у девочки?
2. На столе лежат ручки и карандаши, известно, что ручек на столе 6, а карандашей на 2 меньше, сколько ручек и сколько карандашей на столе?
3. У Вани на шесть монет больше, чем у Тани, а у Тани в два раза меньше, чем у Ани, сколько монет у каждого ребёнка, если у Вани и Ани одинаковое количество монет?

Составим уравнения по каждой из задач.

• В первом случае нам не известно число яблок у девочки, то есть оно равно Х, мы знаем, что Х в 2 раза меньше 6, то есть 6 = 2Х, следовательно, к этому условию подходит уравнение №2.
• Во втором случае за Х обозначается количество карандашей, тогда количество ручек Х + 2, но при этом мы знаем, что ручек 6, то есть Х + 2 = 6, значит сюда подходит третье уравнение.
• Что касается последней задачи, под номером 3, количество Таниных монет, которое встречается в двух условиях, является искомым неизвестным, тогда у Вани 6 + Х монет, а у Ани 2Х монет, то есть 6 + Х = 2Х – очевидно, что сюда подходит первое уравнение.

Если у вас есть задачи, решаемые с помощью уравнения, к которым необходимо подобрать соответствующее равенство, то составьте уравнение для каждой из задач, а потом уже соотносите то, что получилось у вас, с данными уравнениями.

Видео:Математика 6 класс (Урок№52 - Решение задач с помощью уравнений. Часть 2.)Скачать

Усложняем: система уравнений — конфеты

Следующий этап применения буквенных равенств в алгебре – это задачи, решаемые системой уравнений. В них имеется два неизвестных, причём одно из них выражается через другое на основании имеющихся данных. Известно, что у Паши и Кати вместе 20 конфет. Ещё известно, что если бы у Паши было на 2 конфеты больше, то у него было бы 15 конфет, сколько конфет у каждого?

В данном случае мы не знаем ни количество Катиных конфет, ни количество Сашиных конфет, следовательно, у нас два неизвестных, Х и Y соответственно. Вместе с тем, мы знаем, что Y + 2 = 15.

Составив систему, получаем два уравнения:

А дальше действуем по правилам решения систем: выводим Y из второго уравнения, получая Y = 15 — 2, а потом подставляем его в первое, то есть Х + Y = Х + (15 — 2) = 20. Решив уравнение, получаем Х = 7, тогда Y = 20 — 7 = 13. Проверяем правильность решения, подставив Y во второе уравнение: 13 + 2 действительно равно 15, то есть у Кати 7 конфет, а у Паши — 13.

Видео:Решение задач с помощью уравненийСкачать

Ещё сложнее: квадратные уравнения и земельный участок

Встречаются также и задачи по алгебре, решаемые квадратным уравнением. В них нет ничего сложного, просто стандартная система преобразовывается в квадратное уравнение в ходе решения. Например, дан участок земли площадью в 6 гектаров (60000 квадратных метров), забор, огораживающий его, имеет длину 1000 метров. Каковы длина и ширина участка?

Составляем уравнения. Длина забора является периметром участка, следовательно, если длину обозначить Х, а ширину Y, то 1000 = 2 * (Х + Y). Площадь же, то есть Х * Y = 60000. Из первого уравнения выводим Х = 500 — Y. Подставляя его во второе уравнение, получаем (500 — Y) * Y = 60000, то есть 500Y — Y 2 = 60000. Решив уравнение, получаем стороны равные 200 и 300 метрам – квадратное уравнение имеет два корня, один из которых зачастую не подходит по условию, например, является отрицательным, тогда как ответ должен быть числом натуральным, поэтому проверку проводить обязательно.

Видео:Решение задач с помощью уравнений. 6 классСкачать

Повторяем: деревья в саду

Закрепляя тему, решим ещё одну задачу. В саду есть несколько яблонь, 6 груш и несколько вишнёвых деревьев. Известно, что общее количество деревьев в 5 раз больше, чем количество яблонь, при этом вишневых деревьев в 2 раза больше, чем яблоневых. Сколько деревьев каждого вида в саду и сколько в саду всего деревьев?

За неизвестное Х, как, наверное, уже понятно, обозначаем яблоневые деревья, через которые мы сможем выразить остальные величины. Известно, что Y = 2X, а Y + Х + 6 = 5Х. Подставив Y из первого уравнения, получаем равенство 2Х + Х + 6 = 5Х, откуда Х = 3, следовательно в саду Y = 3 * 2 = 6 вишнёвых деревьев. Проводим проверку и отвечаем на второй вопрос, складывая получившиеся величины: 3 + 6 + 6 = 3 * 5, то есть задача решена верно.

Видео:РЕШЕНИЕ ЗАДАЧ С ПОМОЩЬЮ УРАВНЕНИЙ. §3 алгебра 7 классСкачать

Контрольная: сумма чисел

Решение задач с помощью уравнения далеко не такое сложное, как кажется на первый взгляд. Главное – не ошибиться в выборе неизвестного и, что ещё важнее, правильно его выразить, особенно если речь идёт о системе уравнений. В завершение даётся последняя задача, гораздо более запутанная, чем представленные выше.

Сумма трёх чисел – 40. Известно, что Х = 2Y + 3Z, а Y = Z — 2 / 3. Чему равны Х, Y и Z?

Итак, начнём с избавления от первого неизвестного. Вместо Х подставляем в равенство соответствующее выражение, получаем 2Y + 3Z + Z + Y = 3Y + 4Z = 40. Далее заменяем также известный Y, получая равенство 3Z — 2 + 4Z = 40, откуда Z = 6. Возвращаясь к Y, находим, что он равен 5.2, а Х, в свою очередь, равен 18. С помощью проверки убеждаемся в истинности выражения, следовательно задача решена правильно.

Видео:РЕШЕНИЕ ЗАДАЧ С ПОМОЩЬЮ УРАВНЕНИЙ решение уравнений 7 МакарычевСкачать

Заключение

Итак, что же такое задачи, решаемые с помощью уравнения? Так ли они страшны, как кажется на первый взгляд? Ни в коем случае! При должной усидчивости разобраться в них не составляет никакого труда. А однажды поняв алгоритм, в дальнейшем вы сможете щёлкать подобные задачки, даже самые запутанные, как семечки. Главное – внимательность, именно она поможет правильно определить неизвестное и путём решения порой множества уравнений найти ответ.

🌟 Видео

Алгоритм решения задач с помощью систем уравнений. Практическая часть. 9 класс.Скачать

Уравнение. Практическая часть - решение задачи. 2 часть. 5 класс.Скачать

Решение задач с помощью квадратных уравнений. Алгебра, 8 классСкачать

Видеоурок «Решение задач с помощью уравнений»Скачать

Решение задач с помощью уравнений, 6 классСкачать