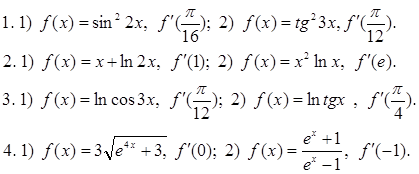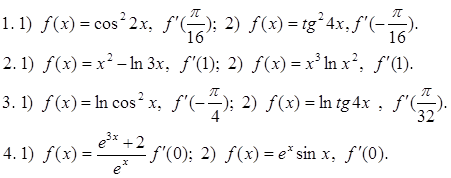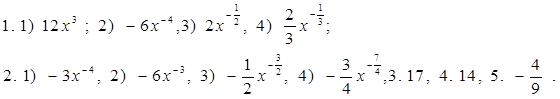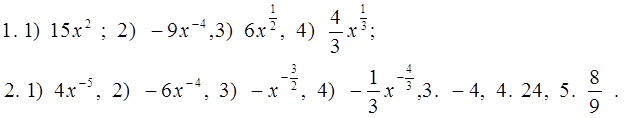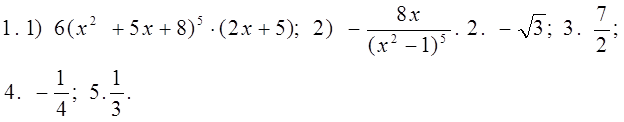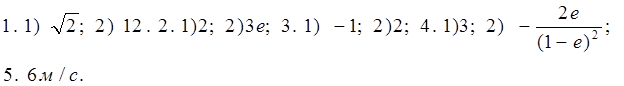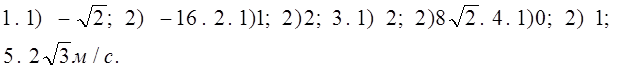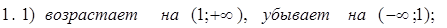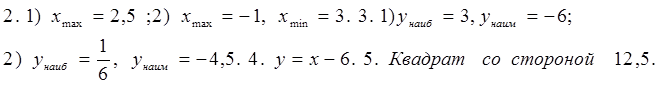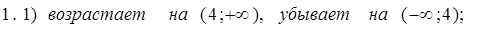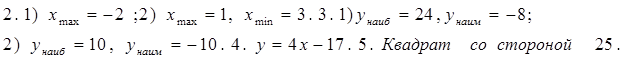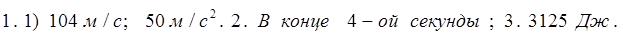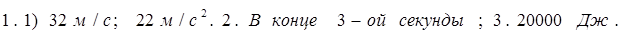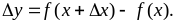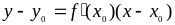Самостоятельная работа уравнения с производной

Самостоятельная работа по теме «Производные»

Найдите производную функции

1) у=х 2 -7х; 2) ; 3) ; 4) у= sinx +3; 5) y = x 5 +9 x 20 +1;

6) у=(х 2 -1)·(х 4 +2); 7) ; 8) у=х· cosx; 9) ;

10) ; 11) ; 12) .

Самостоятельная работа по теме «Производные»

Найдите производную функции

1) у=х 3 -5х; 2) ; 3) ; 4) у=3·со sx +7х; 5) y = x 12 +4 x 17 +х;

6) у=(2х 2 +5)·(3х 4 -2); 7) ; 8) у=х· sinx ; 9) ;

10) ; 11) ; 12) .

Самостоятельная работа по теме «Производные».

Найдите производную функции

1) у=х 3 +2х 5 ; 2) ; 3) ; 4) у= tgx +3; 5) y = x 6 +13 x 10 +12;

6) у=(х 2 +3 )·(х 6 -1 ); 7) ; 8) у=х 2 · cosx ; 9) ;

10) ; 11) ; 12) .

Самостоятельная работа по теме «Производные»

Найдите производную функции

1) у=х 5 -6х; 2) ; 3) ; 4) у=3·с tgx +7х 2 ; 5) y = x 6 -6 x 10 +12х;

6) у=(х 2 -2 )·(х 7 +4 ); 7) ; 8) у= 9) ;

10) ; 11) ; 12) .

Самостоятельная работа по теме «Производные»

Найдите производную функции

1) у=5х 3 -9х+4; 2) ; 3) ; 4) у=4 sinx +9; 5) y = x 9 -6 x 21 -36;

6) у=(х 2 -1)·(х 7 + 4 ); 7) ; 8) у= (2 х +1) · cosx ; 9) ;

10) ; 11) ; 12) .

Самостоятельная работа по теме «Производные»

Найдите производную функции

1) у=х 2 +15х-4; 2) ; 3) ; 4) у=4со sx -9х; 5) y = x 7 -4 x 16 -3;

6) у=(х 2 +5)·(3х 4 — 4 ); 7) ; 8) у= ( х -2) · sinx ; 9) ;

10) ; 11) ; 12) .

Самостоятельная работа по теме «Производные».

Найдите производную функции

1) у=х 3 +2х; 2) ; 3) ; 4) у=3 tgx +4 x -9; 5) y = 4 x 7 -19 x 11 +1;

6) у=(х 2 + 9 )·(х 6 -1 0 ); 7) ; 8) у= ( х 2 +1) · cosx ; 9) ;

10) ; 11) ; 12) .

Самостоятельная работа по теме «Производные»

Найдите производную функции

1) у=2х 5 +6х 2 +9; 2) ; 3) ; 4) у=4·с tgx +12х 2 ;

5) y = x 16 +4 x 9 -11х; 6) у=(х 4 +3)·(х 6 -2); 7) ; 8) у= ;

9) ; 10) ; 11) ; 12) .

Самостоятельная работа по теме «Производные»

Найдите производную функции

1) у=х 2 -7х; 2) ; 3) ; 4) у= sinx +3; 5) y = x 5 +9 x 20 +1;

6) у=(х 2 -1)·(х 4 +2); 7) ; 8) у=х· cosx ; 9) ;

10) ; 11) ; 12) .

Самостоятельная работа по теме «Производные»

Найдите производную функции

1) у=х 3 -5х; 2) ; 3) ; 4) у=3·со sx +7х; 5) y = x 12 +4 x 17 +х;

6) у=(2х 2 +5)·(3х 4 -2); 7) ; 8) у=х· sinx ; 9) ;

10) ; 11) ; 12) .

Самостоятельная работа по теме «Производные».

Найдите производную функции

1) у=х 3 +2х 5 ; 2) ; 3) ; 4) у= tgx +3; 5) y = x 6 +13 x 10 +12;

6) у=(х 2 +3)·(х 6 -1); 7) ; 8) у=х 2 · cosx ; 9) ;

10) ; 11) ; 12) .

Самостоятельная работа по теме «Производные»

Найдите производную функции

1) у=х 5 -6х; 2) ; 3) ; 4) у=3·с tgx +7х 2 ; 5) y = x 6 -6 x 10 +12х;

6) у=(х 2 -2 )·(х 7 +4 ); 7) ; 8) у= 9) ;

10) ; 11) ; 12) .

Самостоятельная работа по теме «Производные»

Найдите производную функции

1) у=5х 3 -9х+4; 2) ; 3) ; 4) у=4 sinx +9; 5) y = x 9 -6 x 21 -36;

6) у=(х 2 -1)·(х 7 +4); 7) ; 8) у=(2х+1)· cosx ; 9) ;

10) ; 11) ; 12) .

Самостоятельная работа по теме «Производные»

Найдите производную функции

1) у=х 2 +15х-4; 2) ; 3) ; 4) у=4со sx -9х; 5) y = x 7 -4 x 16 -3;

6) у=(х 2 +5)·(3х 4 — 4 ); 7) ; 8) у= ( х -2) · sinx ; 9) ;

10) ; 11) ; 12) .

Самостоятельная работа по теме «Производные».

Найдите производную функции

1) у=х 3 +2х; 2) ; 3) ; 4) у=3 tgx +4 x -9; 5) y = 4 x 7 -19 x 11 +1;

6) у=(х 2 +9)·(х 6 -10); 7) ; 8) у=(х 2 +1)· cosx ; 9) ;

10) ; 11) ; 12) .

Самостоятельная работа по теме «Производные»

Найдите производную функции

1) у=2х 5 +6х 2 +9; 2) ; 3) ; 4) у=4·с tgx +12х 2 ;

5) y = x 1 6 +4x 9 — 1 1 х; 6) у=(х 4 +3 )·(х 6 -2 ); 7) ; 8) у= ;

9) ; 10) ; 11) ; 12) .

Самостоятельная работа по теме «Производные»

Найдите производную функции

1) у=х 2 -7х; 2) ; 3) ; 4) у= sinx +3; 5) y = x 5 +9 x 20 +1;

6) у=(х 2 -1)·(х 4 +2); 7) ; 8) у=х· cosx; 9) ;

10) ; 11) ; 12) .

Самостоятельная работа по теме «Производные»

Найдите производную функции

1) у=х 3 -5х; 2) ; 3) ; 4) у=3·со sx +7х; 5) y = x 12 +4 x 17 +х;

6) у=(2х 2 +5)·(3х 4 -2); 7) ; 8) у=х· sinx ; 9) ;

10) ; 11) ; 12) .

Самостоятельная работа по теме «Производные».

Найдите производную функции

1) у=х 3 +2х 5 ; 2) ; 3) ; 4) у= tgx +3; 5) y = x 6 +13 x 10 +12;

6) у=(х 2 +3)·(х 6 -1); 7) ; 8) у=х 2 · cosx ; 9) ;

10) ; 11) ; 12) .

Самостоятельная работа по теме «Производные»

Найдите производную функции

1) у=х 5 -6х; 2) ; 3) ; 4) у=3·с tgx +7х 2 ; 5) y = x 6 -6 x 10 +12х;

6) у=(х 2 -2 )·(х 7 +4 ); 7) ; 8) у= 9) ;

10) ; 11) ; 12) .

Самостоятельная работа по теме «Производные»

Найдите производную функции

1) у=5х 3 -9х+4; 2) ; 3) ; 4) у=4 sinx +9; 5) y = x 9 -6 x 21 -36;

6) у=(х 2 -1)·(х 7 +4); 7) ; 8) у=(2х+1)· cosx ; 9) ;

10) ; 11) ; 12) .

Самостоятельная работа по теме «Производные»

Найдите производную функции

1) у=х 2 +15х-4; 2) ; 3) ; 4) у=4со sx -9х; 5) y = x 7 -4 x 16 -3;

6) у=(х 2 +5)·(3х 4 — 4 ); 7) ; 8) у= ( х -2) · sinx ; 9) ;

10) ; 11) ; 12) .

Самостоятельная работа по теме «Производные».

Найдите производную функции

1) у=х 3 +2х; 2) ; 3) ; 4) у=3 tgx +4 x -9; 5) y = 4 x 7 -19 x 11 +1;

6) у=(х 2 +9)·(х 6 -10); 7) ; 8) у=(х 2 +1)· cosx ; 9) ;

10) ; 11) ; 12) .

Самостоятельная работа по теме «Производные»

Найдите производную функции

1) у=2х 5 +6х 2 +9; 2) ; 3) ; 4) у=4·с tgx +12х 2 ;

5) y = x 1 6 +4x 9 — 1 1 х; 6) у=(х 4 +3 )·(х 6 -2 ); 7) ; 8) у= ;

9) ; 10) ; 11) ; 12) .

Самостоятельная работа по теме «Производные».

Найдите производную функции

1) у=х 3 +2х; 2) ; 3) ; 4) у=3 tgx +4 x -9; 5) y = 4 x 7 -19 x 11 +1;

6) у=(х 2 +9)·(х 6 -10); 7) ; 8) у=(х 2 +1)· cosx ; 9) ;

10) ; 11) ; 12) .

Самостоятельная работа по теме «Производные»

Найдите производную функции

1) у=2х 5 +6х 2 +9; 2) ; 3) ; 4) у=4·с tgx +12х 2 ;

5) y = x 16 +4 x 9 -11х; 6) у=(х 4 +3)·(х 6 -2); 7) ; 8) у= ;

9) ; 10) ; 11) ; 12) .

Самостоятельная работа по теме «Производные».

Найдите производную функции

1) у=х 3 +2х; 2) ; 3) ; 4) у=3 tgx +4 x -9; 5) y = 4 x 7 -19 x 11 +1;

6) у=(х 2 +9)·(х 6 -10); 7) ; 8) у=(х 2 +1)· cosx ; 9) ;

10) ; 11) ; 12) .

Самостоятельная работа по теме «Производные»

Найдите производную функции

1) у=2х 5 +6х 2 +9; 2) ; 3) ; 4) у=4·с tgx +12х 2 ;

5) y = x 1 6 +4x 9 — 1 1 х; 6) у=(х 4 +3 )·(х 6 -2 ); 7) ; 8) у= ;

9) ; 10) ; 11) ; 12) .

Видео:Производная: секретные методы решения. Готовимся к ЕГЭ | Математика TutorOnlineСкачать

Самостоятельные работы по теме «Производная» 10-11 класс.

МУНИЦИПАЛЬНОЕ БЮДЖЕТНОЕ УЧРЕЖДЕНИЕ

г. о. Тольятти, Самарской области

Самостоятельные работы по теме

Автор: Родионова Галина Михайловна,

г. о. Тольятти, Самарской области

Самостоятельные работы по теме «Производная»

С -1. Производная степени и корня

1) Найдите производную функции:

1. 1) у = 3х 4 ; 2) у = 2 х — 3 ; 3) у = 4 ; 4) у = .

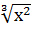
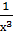
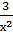
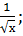
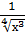
2. 1) у = ; 2) у = ; 3) у = 4) у = .

2) Вычислите производные при заданном значении аргумента:

1. f(x) = 4 x 3 – 3x 2 – x – 1, f / (- 1).

2. f(x) = (2 x 3 – 1)(x 2 + 1), f / ( 1).

3. f(x) = 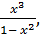f / ( 2).

1) Найдите производную функции:

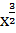
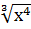
1. 1) у = 5х 3 ; 2) у = 3 х — 3 ; 3) у = 4 ; 4) у = .

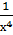
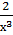
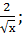
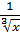
2. 1) у = — ; 2) у = ; 3) у = 4) у = .

2) Вычислите производные при заданном значении аргумента:

1. f ( x ) = 3 x 4 – 2x 2 + 4x – 1, f / (- 1).

2. f ( x ) = ( 3 x 3 + 1)( x 3 — 1), f / ( — 1 ).

3. f(x) = 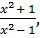f / ( — 2).

C -2. Производная сложной функции

1). Найдите производную функции:

1.1) у = (х 2 + 5 x + 8) 6 ; 2) у = .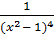

2). Вычислите производные при заданном значении аргумента:

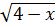
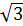
1. f(x) = 2 , f / ( ).

2. f(x) = x 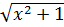, f / ( ).

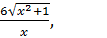
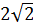
3. f(x) = f / ( ).

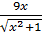
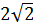
4. f ( x ) = , f / ( ).

1). Найдите производную функции:

1. у = (х 3 — 4 x 2 + 3) 7 ; 2) у = .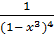

2). Вычислите производные при заданном значении аргумента:

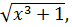
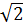
1. f(x) = , f / ( ).

2. f(x) = x 2 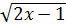, f / (1).

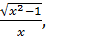
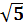
3. f(x) = f / ( ).

4. f ( x ) = 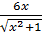, f / ( ).

C — 3. Производные тригонометрической, логарифмической и показательной функций:

Вычислите производные при данном значении аргумента:

Вычислите производные при данном значении аргумента:

С — 4. Геометрический смысл производной

1. Найдите интервалы возрастания и убывания функции:

1) y = x 4 — 4x + 4; 2) y = x 3 — 6x 2 + 4;

2. Исследуйте на максимум и минимум функции:

1) y = — x 2 + 5x – 4; 2) y = 1/3 x 3 — x 2 – 3x + 1/3;

3. Найдите наибольшее и наименьшее значения функции на данном отрезке:

1) y = x 2 — 6x + 4; 0 ≤ x ≤ 5 ;

2) y = 1/2 x 2 – 1/3 x 3 ; 1 ≤ x ≤ 3;

4. Составьте уравнение касательной к параболе

y = x 2 — 7 x + 10 в точке х = 4;

5. Каким должен быть прямоугольник наибольшей площади, который можно согнуть из куска проволоки длиной 50 см.

1. Найдите интервалы возрастания и убывания функции:

1) y = x 2 — 8x + 12; 2) y = — 1/4x 4 — x — 1;

2. Исследуйте на максимум и минимум функции:

1) y = x 2 — 8x + 12; 2) y = 1/3 x 3 + 1/3 x 2 – 2x — 1/3;

3. Найдите наибольшее и наименьшее значения функции на данном отрезке:

1) y = x 2 — 8x + 4; — 2 ≤ x ≤ 5 ;

2) y = — x 2 + 9x 3 – 24 x + 10; 0 ≤ x ≤ 3;

4. Составьте уравнение касательной к параболе

y = x 2 — 6 x + 8 в точке х = 5;

5. Каким должен быть прямоугольник наибольшей площади, который можно согнуть из куска проволоки длиной 100 см.

C — 5. Физический смысл производной

1. Точка движется прямолинейно по закону

s = 2 t 3 + t 2 – 4.

Найдите скорость и ускорение в момент времени t = 4 c .

2. Точка движется прямолинейно по закону s = t 2 – 8 t + 4.

В какой момент времени скорость точки окажется равной нулю?

3. Тело массой 10 кг движется прямолинейно по закону

s = 3 t 2 + t + 4. Найдите кинетическую энергию тела ( mv 2 /2) через 4 с.

1. Точка движется прямолинейно по закону

s = t 3 + 5 t 2 + 4.

Найдите скорость и ускорение в момент времени t = 2 c .

2. Точка движется прямолинейно по закону s = 6 t – t 2 .

В какой момент времени скорость точки окажется равной нулю?

3. Тело массой 100 кг движется прямолинейно по закону

s = 5 t 2 — 4. Найдите кинетическую энергию тела ( mv 2 /2) через 2 с.

С- 3

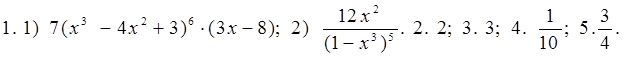
1. Учебник «Алгебра и начала анализа».10-11 классы:

[Ш. А. Алимов и др.] — 7-е изд.-М.: Просвещение,2019

2. Математика. Контрольные и проверочные работы: 10-11 кл. / Н.В. Богомолов. — М.: «Издательство Астрель» 2002.

Видео:АЛГЕБРА С НУЛЯ — Что такое Производная?Скачать

Самостоятельные работы по теме: «Производная функции»

Методические указания по выполнению самостоятельной работы по теме «Производная функции»

Просмотр содержимого документа
«Самостоятельные работы по теме: «Производная функции»»

МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ САМОСТОЯТЕЛЬНОЙ РАБОТЫ № 2

ТЕМА «Производная функции»

Цель: закрепить правила вычисления производных, отработать навыки и умения вычислять производные, развивать умение логически мыслить, формировать умение самоконтроля.

Для выполнения самостоятельной работы обучающийся должен знать определение производной, таблицу производных, правила дифференцирования, правило вычисления производной сложной функции.

Производная и первообразная функции, ее геометрический и физический смысл.

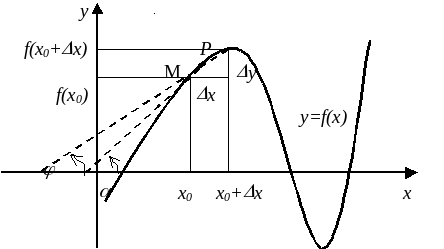
Пусть на некотором промежутке определена некоторая функция

Вычисление производной функции производится по общему правилу дифференцирования:

Придавая аргументу приращение и подставляя в выражение функции вместо аргумента наращенное значение + , находим наращенное значение функции:

Вычитая из наращенного значения функции ее первоначальное значение, находим приращение функции:

Делим приращение функции на приращение аргумента , т.е. составляем отношение:

.

Находим предел этого отношения при :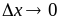

.

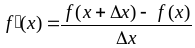
Этот предел и есть производная от функции 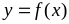. Итак:

Производной функции f(x) в точке х=х₀ называется отношение приращения функции 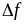в этой точке к приращению аргумента, при стремлении последнего к нулю.

.

Нахождение производной называется дифференцированием.

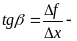
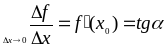
Пусть f(x) определена на некотором промежутке (a, b). Тогда тангенс угла наклона секущей МР к графику функции (рис.10).

,

Угол между кривыми может быть определен как угол между касательными, проведенными к этим кривым в какой- либо точке.

Уравнение касательной к кривой:

Уравнение нормали к кривой: .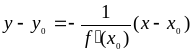

Фактически производная функции показывает скорость изменения функции, т.е. как изменяется функция при изменении переменной.

Физический смысл производной функции f(t), где t— время, а f(t)— закон движения (изменения координат) – мгновенная скорость движения.

Соответственно, вторая производная функции — скорость изменения скорости, т.е. ускорение.

Основные правила дифференцирования.

3) Производная частного: 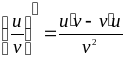, если v ¹ 0

4) Производная сложной функции:

Функция F(x) называется первообразной функцией функции f(x) на отрезке [a, b], если в любой точке этого отрезка верно равенство:

Надо отметить, что первообразных для одной и той же функции может быть бесконечно много. Они будут отличаться друг от друга на некоторое постоянное число.

Неопределенным интегралом функции f(x) называется совокупность первообразных функций, которые определены соотношением:

Условием существования неопределенного интеграла на некотором отрезке является непрерывность функции на этом отрезке.

Таблица производных и первообразных некоторых основных элементарных функций.

🎦 Видео

4. Вычисление производных примеры. Самое начало.Скачать

Производная показательной функции. 11 класс.Скачать

Математика Без Ху!ни. Производная сложной функции.Скачать

Производная функции. 10 класс.Скачать

Контрольная работа. Уравнения с МОДУЛЕМСкачать

5. Производная сложной функции примеры №1.Скачать

Алгебра. 10 класс. Урок 4. Подготовка к контрольной работе по производной.Скачать

Как решать уравнения с модулем или Математический торт с кремом (часть 1) | МатематикаСкачать

05.10.2023 Практика 9. Уравнения, не разрешенные относительно производнойСкачать

ДУ Уравнения, не разрешенные относительно производнойСкачать

Вычисление производных. 10 класс.Скачать

Математика без Ху!ни. Частные производные функции нескольких переменных. Градиент.Скачать

Контрольная производные 11 классСкачать

Производная сложной функции. 10 класс.Скачать

Реакция на результаты ЕГЭ 2022 по русскому языкуСкачать

Простейшие уравнения в частных производныхСкачать

Уравнения в частных производных первого порядка| poporyadku.schoolСкачать