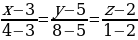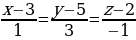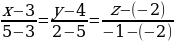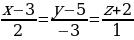Самостоятельная работа уравнение прямой в пространстве

Самостоятельная работа по теме «Уравнение прямой»

Видео:Уравнение прямой в пространстве. 11 класс.Скачать

Скачать:

Видео:11. Прямая в пространстве и ее уравненияСкачать

Предварительный просмотр:

Самостоятельная работа по теме «Уравнение прямой»

1. Напишите уравнение прямой, проходящей через точки А(1; 3) и В(-2; -3).
2. Координаты вершин треугольника А (2; −6), В (4; 2) и С (0; −4). Напишите уравнение прямой, содержащей среднюю линию треугольника, которая параллельна стороне АС.
3. Выясните взаимное расположение окружности, заданной уравнением (х — 3) 2 + (y + 5) 2 = 25 и прямой у = — 1. При наличии точек пересечения указать их в ответе.

Самостоятельная работа по теме «Уравнение прямой»

1. Напишите уравнение прямой, проходящей через точки M(3; 5) и N(-6; -1).
2. Координаты вершин треугольника А (4; −8), В (−2; 6) и С (2; 4). Напишите уравнение прямой, содержащей среднюю линию треугольника, которая параллельна стороне АС.
3. Выясните взаимное расположение окружности, заданной уравнением (х + 7) 2 + (y + 4) 2 = 25 и прямой у = — 7. При наличии точек пересечения указать их в ответе.

Самостоятельная работа по теме «Уравнение прямой»

1. Напишите уравнение прямой, проходящей через точки А(1; 3) и В(-2; -3).
2. Координаты вершин треугольника А (2; −6), В (4; 2) и С (0; −4). Напишите уравнение прямой, содержащей среднюю линию треугольника, которая параллельна стороне АС.
3. Выясните взаимное расположение окружности, заданной уравнением (х — 3) 2 + (y + 5) 2 = 25 и прямой у = — 1. При наличии точек пересечения указать их в ответе.

Самостоятельная работа по теме «Уравнение прямой»

1. Напишите уравнение прямой, проходящей через точки А(1; 3) и В(-2; -3).
2. Координаты вершин треугольника А (2; −6), В (4; 2) и С (0; −4). Напишите уравнение прямой, содержащей среднюю линию треугольника, которая параллельна стороне АС.
3. Выясните взаимное расположение окружности, заданной уравнением (х — 3) 2 + (y + 5) 2 = 25 и прямой у = — 1. При наличии точек пересечения указать их в ответе.

Самостоятельная работа по теме «Уравнение прямой»

1. Напишите уравнение прямой, проходящей через точки M(3; 5) и N(-6; -1).
2. Координаты вершин треугольника А (4; −8), В (−2; 6) и С (2; 4). Напишите уравнение прямой, содержащей среднюю линию треугольника, которая параллельна стороне АС.
3. Выясните взаимное расположение окружности, заданной уравнением (х + 7) 2 + (y + 4) 2 = 25 и прямой у = — 7. При наличии точек пересечения указать их в ответе.

Самостоятельная работа по теме «Уравнение прямой»

1. Напишите уравнение прямой, проходящей через точки M(3; 5) и N(-6; -1).
2. Координаты вершин треугольника А (4; −8), В (−2; 6) и С (2; 4). Напишите уравнение прямой, содержащей среднюю линию треугольника, которая параллельна стороне АС.
3. Выясните взаимное расположение окружности, заданной уравнением (х + 7) 2 + (y + 4) 2 = 25 и прямой у = — 7. При наличии точек пересечения указать их в ответе.

Видео:Уравнение прямой в пространстве через 2 точки. 11 класс.Скачать

Уравнение прямой, плоскости и сферы

306 гр. Математика. Дистанционное обучение. Тема 1-3.

Просмотр содержимого документа
«Уравнение прямой, плоскости и сферы»

Тема 1: Уравнение прямой в пространстве.

З адание: записать конспект и выполнить самостоятельную работу.

Пример 1. Составить уравнение прямой, проходящей через две точки:

Подставив в уравнение прямой соответствующие координаты, получим:

Упростим:

Ответ:

Пример 2. Составить уравнение прямой, проходящей через две точки:

Подставив в уравнение прямой соответствующие координаты, получим:

Упростим:

Ответ: 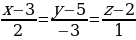Самостоятельная работа

Пример 1. Составить уравнение прямой, проходящей через две точки:

Пример 2. Составить уравнение прямой, проходящей через две точки:

Пример 3. Составить уравнение прямой, проходящей через две точки:

Тема 2: Уравнение плоскости в пространстве

Задание: записать конспект и выполнить самостоятельную работу

П 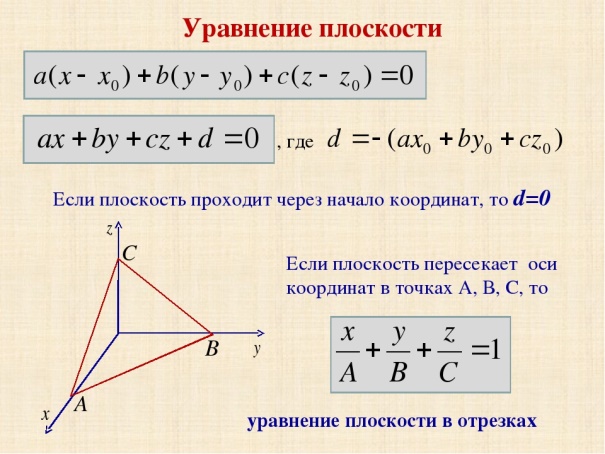ример 1: Принадлежит, ли точка В (-1; 2; 7) плоскости, заданной уравнением 2х+3у-z+3=0

Решение: Подставим координаты точки в уравнение и проверим верно ли равенство.

Ответ: точка В (-1; 2; 7) принадлежит плоскости.

Пример 2: Принадлежит, ли точка Е(0; 4; -6) плоскости, заданной уравнением х-5у-4z+2=0

Решение: Подставим координаты точки в уравнение и проверим верно ли равенство. х-5у-4z+2=0

0-5·4-4·(-6)+2=0-20+24+2=6≠0 не верно

Ответ: точка Е(0; 4; -6) не принадлежит плоскости.

Пример 3: При каком D точка А(1; 5;-2) принадлежит плоскости -3х+2у-z+D=0

Решение: Подставим координаты точки в уравнение и найдем D.

Пример 1: Принадлежит, ли точка В (-2; 3; 8) плоскости, заданной уравнением

Пример 2: Принадлежит, ли точка Е(3; 4; -2) плоскости, заданной уравнением

Пример 3: При каком D точка А(2; 4;-1) принадлежит плоскости -2х+5у-z+D=0

Решить задания №1, №2

О пределение. Сферой называется поверхность, состоящая из всех точек пространства, расположенных на данном расстоянии R от данной точки О.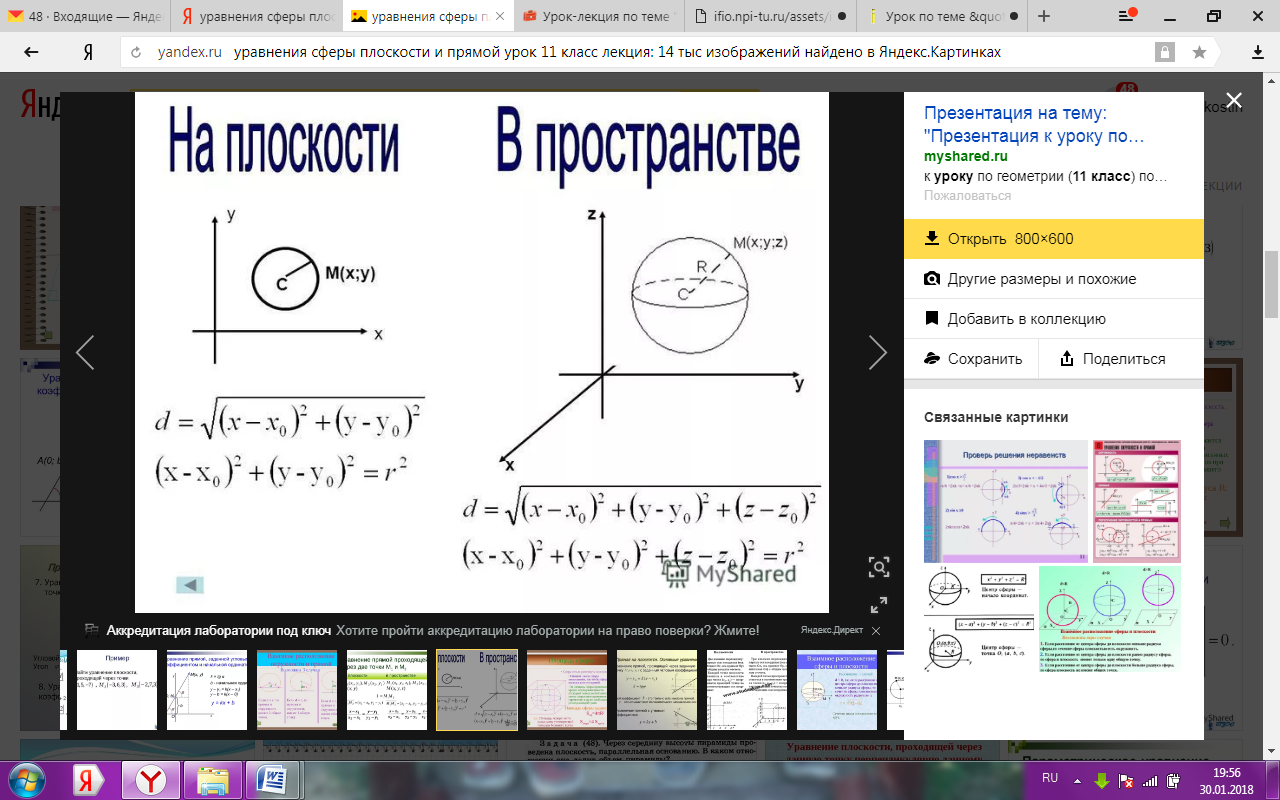

R – радиус сферы, т. О – центр сферы.

Написать уравнение сферы с центром в точке О(1; 2; -5) и радиусом R=3.

Подставим в уравнение сферы: (х-1) 2 +(у-2) 2 +(z-(-5)) 2 =3 2 .

Упростим: (х-1) 2 +(у-2) 2 +(z+5) 2 =9.

Ответ: (х-1) 2 +(у-2) 2 +(z+5) 2 =9.

Пример 2. Дано уравнение сферы: (х-6) 2 +(у+3) 2 +(z-4) 2 =64. Найти координаты центра и радиус сферы.

1)найдем координаты центра: (х-6) 2 +(у-(-3)) 2 +(z-4) 2 =64

2)найдем радиус: R 2 =64, R=√64=8,

Ответ: О(6, -3, 4), R = 8.

Задание 1. Написать уравнение сферы с центром в точке О(5; -2; 3) и радиусом R= 6

Задание 2. Дано уравнение сферы (х-3) 2 +(у+7) 2 +(z-8) 2 =25. Найти координаты центра и радиус сферы.

Видео:Аналитическая геометрия, 6 урок, Уравнение прямойСкачать

Самостоятельная работа по геометрии на тему: «Уравнение прямой» (9 класс)

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

«Актуальность создания школьных служб примирения/медиации в образовательных организациях»

Свидетельство и скидка на обучение каждому участнику

Видео:Стереометрия 10 класс. Часть 1 | МатематикаСкачать

Геометрия 9 класс

Видео:Каноническое уравнение прямой в пространстве. 11 класс.Скачать

Самостоятельная работа по теме:

Видео:12. Уравнения прямой в пространстве Решение задачСкачать

«Уравнение прямой»

1. Проверить, лежат ли точки А (3; -1) и В (-4; -3) на прямой 2х – у + 5 = 0.

2. Построить прямые, заданные уравнениями:

3. Записать уравнение прямой, проходящей через точку М (2; -3), параллельно оси ординат.

4. Записать уравнение прямой, проходящей через точки А (-2; -1) и В (3; 1).

Видео:Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать

Геометрия 9 класс

Видео:Уравнение прямой в пространстве ( решение задач, урок 2)Скачать

Самостоятельная работа по теме:

1. Проверить, лежат ли точки А (-5; 3) и В (9; 4) на прямой х – 4у + 7 = 0.

2. Построить прямые, заданные уравнениями:

3. Записать уравнение прямой, проходящей через точку К (-5; 3), параллельно оси абсцисс.

4. Записать уравнение прямой, проходящей через точки А (-3; -3) и В (3; 5).

Видео:Лекция 28. Виды уравнения прямой в пространстве.Скачать

Геометрия 9 класс

Видео:Математика без Ху!ни. Уравнение плоскости.Скачать

Самостоятельная работа по теме:

Видео:Написать канонические и параметрические уравнения прямой в пространствеСкачать

«Уравнение прямой»

1. Проверить, лежат ли точки А (-2; 5) и В (3; -1) на прямой 3х – у + 2 = 0.

2. Построить прямые, заданные уравнениями:

3. Записать уравнение прямой, проходящей через точку М (6; -2), параллельно оси ординат.

4. Записать уравнение прямой, проходящей через точки А (-2; 3) и В (4; -1).

Видео:Видеоурок "Общие уравнения прямой"Скачать

Геометрия 9 класс

Видео:Составляем уравнение прямой по точкамСкачать

Самостоятельная работа по теме:

Видео:Лекция 23. Виды уравнений прямой на плоскости.Скачать

«Уравнение прямой»

1. Проверить, лежат ли точки А (7; -2) и В (-5; 4) на прямой х + 2у – 3 = 0.

2. Построить прямые, заданные уравнениями:

3. Записать уравнение прямой, проходящей через точку К (-4; 3), параллельно оси абсцисс.

4. Записать уравнение прямой, проходящей через точки А (1; 4) и В (-5; 2).

Видео:ГЕОМЕТРИЯ 9 класс: Уравнение окружности и прямойСкачать

Геометрия 9 класс

Видео:Геометрия 9 класс (Урок№9 - Уравнение линии на плоскости. Уравнение окружности. Уравнение прямой.)Скачать

Самостоятельная работа по теме:

Видео:Каноническое уравнение прямой в пространстве Преход от общего уравненияСкачать

«Уравнение прямой»

1. Проверить, лежат ли точки А (3; -1) и В (-4; -3) на прямой 4х – у + 13 = 0.

2. Построить прямые, заданные уравнениями:

3. Записать уравнение прямой, проходящей через точку М (4; -3), параллельно оси ординат.

4. Записать уравнение прямой, проходящей через точки А (-3; -1) и В (4; 1).

Геометрия 9 класс

Самостоятельная работа по теме:

1. Проверить, лежат ли точки А (-5; 3) и В (10; 4) на прямой х – 3у + 2 = 0.

2. Построить прямые, заданные уравнениями:

3. Записать уравнение прямой, проходящей через точку К (-4; 2), параллельно оси абсцисс.

4. Записать уравнение прямой, проходящей через точки А (-2; -3) и В (3; 4).

Геометрия 9 класс

Самостоятельная работа по теме:

«Уравнение прямой»

1. Проверить, лежат ли точки А (-4; 5) и В (4; -2) на прямой 3х – у + 2 = 0.

2. Построить прямые, заданные уравнениями:

3. Записать уравнение прямой, проходящей через точку М (4; -3), параллельно оси ординат.

4. Записать уравнение прямой, проходящей через точки А (-3; 3) и В (8; -1).

Геометрия 9 класс

Самостоятельная работа по теме:

«Уравнение прямой»

1. Проверить, лежат ли точки А (3; -2) и В (-4; 4) на прямой х + 2у – 3 = 0.

2. Построить прямые, заданные уравнениями:

3. Записать уравнение прямой, проходящей через точку К (-3; 4), параллельно оси абсцисс.

4. Записать уравнение прямой, проходящей через точки А (2; 4) и В (-3; 2).

Геометрия 9 класс

Самостоятельная работа по теме:

«Уравнение прямой»

1. Проверить, лежат ли точки А (3; -1) и В (-4; -3) на прямой 2х – у + 5 = 0.

2. Построить прямые, заданные уравнениями:

3. Записать уравнение прямой, проходящей через точку М (2; -3), параллельно оси ординат.

4. Записать уравнение прямой, проходящей через точки А (-2; -1) и В (3; 1).

Геометрия 9 класс

Самостоятельная работа по теме:

1. Проверить, лежат ли точки А (-5; 3) и В (9; 4) на прямой х – 4у + 7 = 0.

2. Построить прямые, заданные уравнениями:

3. Записать уравнение прямой, проходящей через точку К (-5; 3), параллельно оси абсцисс.

4. Записать уравнение прямой, проходящей через точки А (-3; -3) и В (3; 5).

Геометрия 9 класс

Самостоятельная работа по теме:

«Уравнение прямой»

1. Проверить, лежат ли точки А (-2; 5) и В (3; -1) на прямой 3х – у + 2 = 0.

2. Построить прямые, заданные уравнениями:

3. Записать уравнение прямой, проходящей через точку М (6; -2), параллельно оси ординат.

4. Записать уравнение прямой, проходящей через точки А (-2; 3) и В (4; -1).

Геометрия 9 класс

Самостоятельная работа по теме:

«Уравнение прямой»

1. Проверить, лежат ли точки А (7; -2) и В (-5; 4) на прямой х + 2у – 3 = 0.

2. Построить прямые, заданные уравнениями:

3. Записать уравнение прямой, проходящей через точку К (-4; 3), параллельно оси абсцисс.

4. Записать уравнение прямой, проходящей через точки А (1; 4) и В (-5; 2).

Геометрия 9 класс

Самостоятельная работа по теме:

«Уравнение прямой»

1. Проверить, лежат ли точки А (3; -1) и В (-4; -3) на прямой 4х – у + 13 = 0.

2. Построить прямые, заданные уравнениями:

3. Записать уравнение прямой, проходящей через точку М (4; -3), параллельно оси ординат.

4. Записать уравнение прямой, проходящей через точки А (-3; -1) и В (4; 1).

Геометрия 9 класс

Самостоятельная работа по теме:

1. Проверить, лежат ли точки А (-5; 3) и В (10; 4) на прямой х – 3у + 2 = 0.

2. Построить прямые, заданные уравнениями:

3. Записать уравнение прямой, проходящей через точку К (-4; 2), параллельно оси абсцисс.

4. Записать уравнение прямой, проходящей через точки А (-2; -3) и В (3; 4).

Геометрия 9 класс

Самостоятельная работа по теме:

«Уравнение прямой»

1. Проверить, лежат ли точки А (-4; 5) и В (4; -2) на прямой 3х – у + 2 = 0.

2. Построить прямые, заданные уравнениями:

3. Записать уравнение прямой, проходящей через точку М (4; -3), параллельно оси ординат.

4. Записать уравнение прямой, проходящей через точки А (-3; 3) и В (8; -1).

Геометрия 9 класс

Самостоятельная работа по теме:

«Уравнение прямой»

1. Проверить, лежат ли точки А (3; -2) и В (-4; 4) на прямой х + 2у – 3 = 0.

2. Построить прямые, заданные уравнениями:

3. Записать уравнение прямой, проходящей через точку К (-3; 4), параллельно оси абсцисс.

4. Записать уравнение прямой, проходящей через точки А (2; 4) и В (-3; 2).

Геометрия 9 класс

Самостоятельная работа по теме:

«Уравнение прямой»

1. Проверить, лежат ли точки А (3; -1) и В (-4; -3) на прямой 2х – у + 5 = 0.

2. Построить прямые, заданные уравнениями:

3. Записать уравнение прямой, проходящей через точку М (2; -3), параллельно оси ординат.

4. Записать уравнение прямой, проходящей через точки А (-2; -1) и В (3; 1).

Геометрия 9 класс

Самостоятельная работа по теме:

1. Проверить, лежат ли точки А (-5; 3) и В (9; 4) на прямой х – 4у + 7 = 0.

2. Построить прямые, заданные уравнениями:

3. Записать уравнение прямой, проходящей через точку К (-5; 3), параллельно оси абсцисс.

4. Записать уравнение прямой, проходящей через точки А (-3; -3) и В (3; 5).

Геометрия 9 класс

Самостоятельная работа по теме:

«Уравнение прямой»

1. Проверить, лежат ли точки А (-2; 5) и В (3; -1) на прямой 3х – у + 2 = 0.

2. Построить прямые, заданные уравнениями:

3. Записать уравнение прямой, проходящей через точку М (6; -2), параллельно оси ординат.

4. Записать уравнение прямой, проходящей через точки А (-2; 3) и В (4; -1).

Геометрия 9 класс

Самостоятельная работа по теме:

«Уравнение прямой»

1. Проверить, лежат ли точки А (7; -2) и В (-5; 4) на прямой х + 2у – 3 = 0.

2. Построить прямые, заданные уравнениями:

3. Записать уравнение прямой, проходящей через точку К (-4; 3), параллельно оси абсцисс.

4. Записать уравнение прямой, проходящей через точки А (1; 4) и В (-5; 2).

Геометрия 9 класс

Самостоятельная работа по теме:

«Уравнение прямой»

1. Проверить, лежат ли точки А (3; -1) и В (-4; -3) на прямой 4х – у + 13 = 0.

2. Построить прямые, заданные уравнениями:

3. Записать уравнение прямой, проходящей через точку М (4; -3), параллельно оси ординат.

4. Записать уравнение прямой, проходящей через точки А (-3; -1) и В (4; 1).

Геометрия 9 класс

Самостоятельная работа по теме:

1. Проверить, лежат ли точки А (-5; 3) и В (10; 4) на прямой х – 3у + 2 = 0.

2. Построить прямые, заданные уравнениями:

3. Записать уравнение прямой, проходящей через точку К (-4; 2), параллельно оси абсцисс.

4. Записать уравнение прямой, проходящей через точки А (-2; -3) и В (3; 4).

Геометрия 9 класс

Самостоятельная работа по теме:

«Уравнение прямой»

1. Проверить, лежат ли точки А (-4; 5) и В (4; -2) на прямой 3х – у + 2 = 0.

2. Построить прямые, заданные уравнениями:

3. Записать уравнение прямой, проходящей через точку М (4; -3), параллельно оси ординат.

4. Записать уравнение прямой, проходящей через точки А (-3; 3) и В (8; -1).

Геометрия 9 класс

Самостоятельная работа по теме:

«Уравнение прямой»

1. Проверить, лежат ли точки А (3; -2) и В (-4; 4) на прямой х + 2у – 3 = 0.

2. Построить прямые, заданные уравнениями:

3. Записать уравнение прямой, проходящей через точку К (-3; 4), параллельно оси абсцисс.

4. Записать уравнение прямой, проходящей через точки А (2; 4) и В (-3; 2).

Геометрия 9 класс

Самостоятельная работа по теме:

«Уравнение прямой»

1. Проверить, лежат ли точки А (3; -1) и В (-4; -3) на прямой 2х – у + 5 = 0.

2. Построить прямые, заданные уравнениями:

3. Записать уравнение прямой, проходящей через точку М (2; -3), параллельно оси ординат.

4. Записать уравнение прямой, проходящей через точки А (-2; -1) и В (3; 1).

Геометрия 9 класс

Самостоятельная работа по теме:

1. Проверить, лежат ли точки А (-5; 3) и В (9; 4) на прямой х – 4у + 7 = 0.

2. Построить прямые, заданные уравнениями:

3. Записать уравнение прямой, проходящей через точку К (-5; 3), параллельно оси абсцисс.

4. Записать уравнение прямой, проходящей через точки А (-3; -3) и В (3; 5).

Геометрия 9 класс

Самостоятельная работа по теме:

«Уравнение прямой»

1. Проверить, лежат ли точки А (-2; 5) и В (3; -1) на прямой 3х – у + 2 = 0.

2. Построить прямые, заданные уравнениями:

3. Записать уравнение прямой, проходящей через точку М (6; -2), параллельно оси ординат.

4. Записать уравнение прямой, проходящей через точки А (-2; 3) и В (4; -1).

Геометрия 9 класс

Самостоятельная работа по теме:

«Уравнение прямой»

1. Проверить, лежат ли точки А (7; -2) и В (-5; 4) на прямой х + 2у – 3 = 0.

2. Построить прямые, заданные уравнениями:

3. Записать уравнение прямой, проходящей через точку К (-4; 3), параллельно оси абсцисс.

4. Записать уравнение прямой, проходящей через точки А (1; 4) и В (-5; 2).

Геометрия 9 класс

Самостоятельная работа по теме:

«Уравнение прямой»

1. Проверить, лежат ли точки А (3; -1) и В (-4; -3) на прямой 4х – у + 13 = 0.

2. Построить прямые, заданные уравнениями:

3. Записать уравнение прямой, проходящей через точку М (4; -3), параллельно оси ординат.

4. Записать уравнение прямой, проходящей через точки А (-3; -1) и В (4; 1).

Геометрия 9 класс

Самостоятельная работа по теме:

1. Проверить, лежат ли точки А (-5; 3) и В (10; 4) на прямой х – 3у + 2 = 0.

2. Построить прямые, заданные уравнениями:

3. Записать уравнение прямой, проходящей через точку К (-4; 2), параллельно оси абсцисс.

4. Записать уравнение прямой, проходящей через точки А (-2; -3) и В (3; 4).

Геометрия 9 класс

Самостоятельная работа по теме:

«Уравнение прямой»

1. Проверить, лежат ли точки А (-4; 5) и В (4; -2) на прямой 3х – у + 2 = 0.

2. Построить прямые, заданные уравнениями:

3. Записать уравнение прямой, проходящей через точку М (4; -3), параллельно оси ординат.

4. Записать уравнение прямой, проходящей через точки А (-3; 3) и В (8; -1).

Геометрия 9 класс

Самостоятельная работа по теме:

«Уравнение прямой»

1. Проверить, лежат ли точки А (3; -2) и В (-4; 4) на прямой х + 2у – 3 = 0.

2. Построить прямые, заданные уравнениями:

3. Записать уравнение прямой, проходящей через точку К (-3; 4), параллельно оси абсцисс.

4. Записать уравнение прямой, проходящей через точки А (2; 4) и В (-3; 2).

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

• Сейчас обучается 949 человек из 80 регионов

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

• Сейчас обучается 681 человек из 75 регионов

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

• Сейчас обучается 314 человек из 70 регионов

Ищем педагогов в команду «Инфоурок»

Дистанционные курсы для педагогов

Самые массовые международные дистанционные

Школьные Инфоконкурсы 2022

33 конкурса для учеников 1–11 классов и дошкольников от проекта «Инфоурок»

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

5 568 214 материалов в базе

Материал подходит для УМК

«Геометрия», Мерзляк А.Г., Полонский В.Б., Якир М.С./ Под ред. Подольского В.Е.

§ 10. Уравнение прямой

Другие материалы

• 22.06.2021
• 92
• 1

• 22.06.2021
• 103
• 1

• 22.06.2021
• 59
• 2

• 22.06.2021
• 125
• 7

• 22.06.2021
• 489
• 36

• 22.06.2021
• 1100
• 95

• 21.06.2021
• 78
• 6

• 21.06.2021
• 70
• 4

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Добавить в избранное

• 22.06.2021 2888
• DOCX 124 кбайт
• 212 скачиваний
• Оцените материал:

Настоящий материал опубликован пользователем Зинова Ольга Викторовна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Автор материала

• На сайте: 5 лет и 4 месяца
• Подписчики: 4
• Всего просмотров: 70771
• Всего материалов: 21

Московский институт профессиональной
переподготовки и повышения
квалификации педагогов

Дистанционные курсы
для педагогов

663 курса от 690 рублей

Выбрать курс со скидкой

Выдаём документы
установленного образца!

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

Профессия педагога на третьем месте по популярности среди абитуриентов

Время чтения: 1 минута

Рособрнадзор не планирует переносить досрочный период ЕГЭ

Время чтения: 0 минут

У 76% российских учителей оклад ниже МРОТ

Время чтения: 2 минуты

В Воронеже продлили удаленное обучение для учеников 5-11-х классов

Время чтения: 1 минута

Тринадцатилетняя школьница из Индии разработала приложение против буллинга

Время чтения: 1 минута

Количество бюджетных мест в вузах по IT-программам вырастет до 160 тыс.

Время чтения: 2 минуты

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.